基于机器学习的回流焊焊点形貌预测

范子铭，田富君，胡子翔，魏 李

(1.中国电子科技集团公司第三十八研究所，安徽 合肥 230088；2.国家级工业设计中心(中电38所)，安徽 合肥 230088)

0 引言

随着表面贴装技术(surface mount technology,SMT)的广泛应用，回流焊技术也在不断发展。回流焊是通过将气体加热到一定温度使焊膏融化，继而将元器件焊接在PCB板上，对于回流焊技术而言，焊点形貌作为回流焊技术的评价标准，对于它的检测至关重要。

针对焊点形貌分析一直是研究的重点方向，Wang等[1]针对焊点形貌采用不同的热回流曲线进行分析，得到了加热因子与焊点形貌之间的关系；赵亚楠等[2]以数值与实验相结合的方法研究电阻钎焊，以仿真的方法证明了温度场分布与变化规律； Jin等[3]建立了元器件焊点形貌的物理形状仿真模型，结合回流焊仿真结果对回流焊工艺进行了优化；王星[4]通过Surface Evolver预测焊点形貌，取得了很高的预测准确性；Pan等[5]以数据为驱动建立了一个基于能量的三维模型，分析了焊膏与焊点形貌之间的关系。近年来，随着人工智能的兴起，将数据挖掘技术与焊接相结合成为新的研究方向。陶汪等[6]用人工神经网络的方法成功对激光点焊焊点形貌进行预测； Gao等[7]利用卷积神经网络和SVM对于焊点缺陷进行分析。

目前，针对回流焊的焊点形貌检测多采用传统方法，传统方法虽然检测精度高，但是需要经过试验进行检测，时间周期长，材料利用率低。通过机器学习的方法可以挖掘焊点形貌与工艺参数之间内在关系，通过建立智能预测模型可以在实验之前预测最终结果，帮助工艺人员减少实验次数，从而提高生产效率。

本文提出采用机器学习算法来进行预测焊点形貌，以某SMT生产线采集的钽电容焊点形貌数据为数据集，通过数据挖掘的方法建立针对回流焊的焊点形貌预测模型，并通过实验仿真数据集进行验证该方法的合理性。

1 机器学习模型

本文采用2种机器学习算法搭建回流焊焊点形貌预测模型，分别为BP神经网络和LightGBM算法。

1.1 BP神经网络

BP神经网络(back propagation neural network，BPNN)为误差逆向传播的神经网络[8]，其3层神经元结构如图1所示。

图1 BP神经网络模型

设N、L和M分别为BPNN输入层、隐含层和输出层的节点个数，其中每个节点的输入和权重值分别为xi和wij、wjk，设αj和βk分别为输入层与隐含层和隐含层与输出层之间的偏置值，Yk为期望输出值，神经网络学习速率为γ，则BPNN运算中每次循环迭代后新的权重wij*与wjk*和偏置值αj*与βk*分别为：

(1)

wjk*=wjk+γHjek

(2)

(3)

βk*=βk+γek

(4)

对于BPNN而言，每进行一次梯度下降运算更新一次权值和偏置值，通过循环迭代减小误差值，迭代一直到误差值达到稳定收敛时停止，完成预测模型训练。

1.2 LightGBM算法

LightGBM算法是微软提出的一种基于梯度下降决策树(gradient boosting decision tree，GBDT)算法的机器学习算法，其在GBDT算法的基础上提出单边梯度采样算法(gradient-based one-side sampling，GOSS)算法和特征捆绑算法(exclusive feature bundling，EFB)算法相融合的混合算法来提高预测模型的精度[9-11]。

1.2.1 GOSS算法。

GOSS算法对梯度幅度小的数据集进行忽略，对梯度幅度大的数据集进行采样，以此来减少数据量处理，同时由于这部分数据集梯度幅度大，因此有效信息的增益也相应较大，从而保证预测精度。

假设数据集O上的数据空间中输入部分空间为X，输出部分空间为Y，数据空间中空间向量数量为nO，则GBDT算法首先将输入部分的数据空间映射到梯度空间上。假设数据集上的输入空间向量为xi，数据空间的特征维度为s，gi为第i次循环迭代过程中的梯度下降迭代时所训练算法的损失函数的目标函数的梯度下降方向。则GBDT算法通过遍历所有分裂节点后，在寻找数据空间上的切分点k和切分特征变量J时，划分出的2个数据集分别为R1和R2，则2个数据集中空间向量个数分别为nR1(k)和nR2(k)，则在切分点k产生的数据增益VJ|O(d)为

VJ|O(d)=

(5)

(6)

1.2.2 EFB算法

EFB算法对于高纬度数据集通过将数据特征进行捆绑，以此来降低数据集的维度，提高算法训练的效率。

由于在处理高维数据的时候数据维度过高，为了降低数据维度提高训练效率，EFB算法将数据特征空间存在的特征互斥数据进行捆绑，捆绑之后的互斥多维特征降为单一特征数据。通过EFB算法中的Histogram算法，如图2所示，其构建特征直方图的时间复杂度就会从Data·feature变为Data·Bundle，由于经过捆绑之后的Bundle数据量远远小于Feature数据量，因此提高了训练效率。

图2 Histogram算法流程

EFB算法同时提出了按叶生长的决策树生长策略，如图3所示。按叶生长算法核心思想是通过对所有叶子进行判断，找到其中分裂之后信息增益最大的叶子，然后对该叶子的节点进行分裂，通过这样的循环分裂，最后完成决策树生长，这样每次针对单一节点而不是对所有节点进行分裂，大大降低了运算量，提高运算效率。

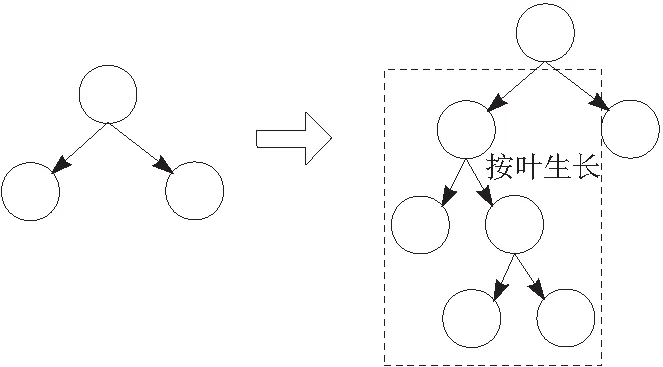
图3 按叶生长决策树生长策略

2 建立基于机器学习的回流焊焊点形貌预测模型

本文使用的回流焊焊点形貌数据集采集于某SMT生产线钽电容焊点形貌，实际数据共1 700条，采集方法如图4所示。影响因素作为输入共3种，分别为峰值温度、降温速率和焊膏厚度，输出结果为3种焊点形貌评价指标，分别为焊点厚度、焊点宽度和焊料爬高。

图4 钽电容回流焊焊点形貌采集

针对采集到的数据集，需要先对数据集进行处理才能满足训练预测模型的需要。数据预处理首先是清洗数据，本文采用准则，设数据量为n，通过Bessel公式计算标准偏差为

(7)

由于数据的维度存在差异，因此需要对数据进行归一化处理。本文采用的归一化方法为min-max标准归一化，即

(8)

通过最大值Xmax与最小值Xmin的极差，按比例将原始数据与[0,1]区间一一映射，得到归一化后的新数据样本X*，完成数据归一化处理。

选择R2(R-Square值)作为评价预测模型精度的标准，该评价指标评估的是预测模型对变量预测的方差的比例，其取值范围在[0,1]之间，越接近1，说明预测模型越准确，越接近0，说明预测模型越没有价值。其公式为

(9)

建立基于机器学习的回流焊焊点形貌预测模型，BP神经网络和LightGBM算法的模型流程分别如图5和图6所示。首先进行程序初始化，对于BPNN神经网络是先将回流焊焊点形貌数据集输入， 通过计算隔层神经元的输出值计算最后输出层

图5 基于BP神经网络的回流焊焊点形貌预测模型流程

图6 基于LightGBM算法的回流焊焊点形貌预测模型流程

的误差，通过误差反向传播修改各层的权值和偏置值，当迭代到设定的误差值范围或者训练集全部训练完毕后，结束迭代输出预测模型；对于LightGBM算法，将训练集输入模型进行训练，先通过EFB算法进行降维处理，再通过GOSS算法计算数据增益，当满足预测效果或者训练集全部训练完毕后，结束迭代输出预测模型。

3 实验结果与讨论

完成建立的基于机器学习算法的回流焊焊点形貌预测模型，其输出的R-Square值如表1所示。

表1 焊点形貌预测R-Square值

由表1可知，基于LightGBM算法建立的钽电容回流焊焊点形貌预测模型的预测准确率高于基于BP神经网络建立的回流焊焊点形貌预测模型。针对LightGBM建立的模型预测如图7～图9所示。

图7 焊点厚度预测

图8 焊点宽度预测

图9 焊料爬高预测

图7a、图8a和图9a为预测散点图，其中三角形为真值，即验证集中的真实值，圆点为预测值，即LightGBM算法建立的预测模型针对训练集中的值进行预测的预测值，可以看出，代表预测值的圆点基本上命中了代表真值的三角星中心，代表该样本的预测值预测准确，仍有个别点偏离真实值较远，说明预测有差距；图7b、图8b和图9b为每个样本的预测值与真实值之间的绝对值误差，可以看出，绝对误差曲线基本在0附近，说明预测值与真实值之间的误差较低，而个别误差较大，说明该样本的预测值与真实值之间差距较大。

对误差原因进行分析，主要可能是以下2种原因：第1是由于预测模型精度不够，还需要对模型进行优化， 同时可能是影响因素种类和数据量不够，可加入更多的数据和数据类型来增加模型的稳定性；第2是由于实际采集数据时存在误差，个别数据采集值不合理，导致个别样本预测准确率不足。

针对上面结果进行影响程度分析，对每个输入进行统计分析，以1 000为总计，对每项输入参数影响最终结果的程度进行评价，每项输入参数的影响程度如图10～图12所示，数字代表在总计1 000中所占的权重。

图10 焊点厚度影响程度

图11 焊点宽度影响程度

图10～图12中，焊膏厚度均是影响最终预测结果最高的输入因素，在图10的焊点厚度中，峰值温度和降温速率影响程度均不高；而在图12的焊料爬高中，峰值温度影响程度占比达到21.9%，而降温速率也达到了12.6%；在图11的焊点宽度中，峰值温度和降温速率影响程度占比分别达到了15.8%和11.6%。总体来看，焊膏厚度是主要影响最终焊点形貌的因素，降温速率是影响最小的因素，因此在进行实验时，主要以焊膏厚度作为变量去修改最终焊点形貌，其他2项作为次要变量对最终结果进行微调。

图12 焊料爬高影响程度

完成预测模型的训练与分析后，将该预测模型应用于该SMT焊点形貌实验数据集，在之前实验中，实验人员通过试凑法和工艺经验在计算机中进行模拟仿真，经过23次实验最终确定为了达到理想焊点形貌所需要的输入参数，由于仿真软件模拟渲染时间较长，总共耗时17 d完成全部实验内容。

本次实验中，实验人员将之前实验的初始设定输入参数值作为预测模型的输入，设定理想的焊点形貌参数值为优化目标，进行参数推荐，经过循环迭代后给出最佳参数。实验人员将模型推荐的参数输入仿真软件进行模拟仿真，结果与所需要的焊点形貌参数差距很小。根据预测模型给出的影响程度所占权重对输入参数进行微调，最终经过4次模拟仿真试验得到理想焊点形貌所需要的输入参数，总耗时2 d。

4 结束语

基于机器学习的方法针对钽电容的回流焊焊点形貌建立预测模型，其中，基于LightGBM算法建立的预测模型的预测精度R-Square值分别达到了0.878 02、0.884 62和0.862 16，预测效果优于基于BPNN算法建立的预测模型。针对预测模型进行参数分析，得出焊膏厚度是主要影响因素，峰值温度和降温速率是次要影响因素，因此在修正输入时，主要考虑修改焊膏厚度，次要考虑修改峰值温度和降温速率。该预测模型在实际使用中，以实验人员理想的输出为最终结果，提供输入参数建议，将原本预计的实验时间减少为原来的1/10，并提供修改参数建议。

本文方法为回流焊实验提供了一个新的思路，传统回流焊焊点形貌检测费时费力，通过建立预测模型的方法可以很快得出预测的最终焊点形貌，根据最终结果和输入参数重要性修改参数，减少仿真模拟实验次数，并通过实际实验验证了该方法的可用性。