基于滑模控制算法的自适应跟车巡航研究

任一凡，孙后环，刘 陈

(南京工业大学机械与动力工程学院，江苏 南京 211816)

0 引言

车辆自适应巡航系统简称ACC系统，作为汽车先进辅助驾驶系统的主要功能之一，在汽车高度智能化的发展中，ACC系统装机率越来越高。ACC系统通过接管部分操纵任务，减轻驾驶员驾驶强度，保证行车安全。随着技术进步，毫米波雷达、激光雷达与摄像头等多传感器在ACC系统中通过信息融合，使物体的识别和车距的探测更加精准。利用不同的上层算法体现了不同的跟车特性，经过不断创新和优化，部分汽车厂商已经能够实现较为成熟的跟车巡航功能[1]。

国内外对跟车巡航中上层控制算法的研究十分广泛。薛杨[2]通过将模糊控制与PID控制结合，设计了安全距离函数对ACC系统控制算法进行辅助调节；刘道旭东[3]将神经网络算法联合PID控制，提高PID控制的ACC系统的响应快速性和精准性；李鹏飞等[4]采用模糊神经网络，依据驾驶数据，训练自动生成隶属函数和模糊规则的模糊神经网络控制器；Xiao等[5]在设计ACC巡航系统时，基于滑模控制理论对理想跟车距离进行分析。目前的汽车自适应跟车系统能够实现跟车巡航功能，但还存在着舒适性和精确性的不足。本文主要改进自适应巡航中跟车巡航部分的速度控制精度，设计合理的可变理想跟车距离，用以提高减速阶段的舒适性和安全性。

1 跟车巡航系统结构

1.1 跟车巡航算法控制总体架构

依据传感器获取系统所需信息，如两车相对距离、本车车速和轮速等数据，并将其反馈到上层算法[6]中，计算出前车车速和定义的理想安全距离，基于优化的滑模变结构算法获取后车跟车的理想加速度。两车行驶状态如图1所示，其中,vf和vx分别为前、后车车速，af和ax分别为前、后车加速度，L为两车实际车间距。

图1 跟车巡航行驶状态

下层控制模块根据获得的理想加速度，计算出发动机需求扭矩，当理想加速度为负时，制动器执行制动减速[7]。整体技术路线如图2所示。

图2 跟车技术路线

1.2 理想跟车距离设计

理想跟车距离是ACC跟车巡航系统的重要指标。车间距保持策略主要有固定时距跟车策略和变时距跟车策略[8]。本文将制动安全距离和制动减速度作为参考量对跟车策略进行改进，设计二次跟车距离策略作为理想跟车间距。二次车距策略模型为

(1)

Dmin为两车静止时需保持的最小距离；T为汽车控制器及执行器系统响应时间；amax为车辆紧急制动时的最大减速度。当目标车辆紧急刹车，一般可以产生7.5～8.0 m/s2的制动减速度[9]，本文amax取7.5 m/s2。

式(1)假定前车以最大减速度减速的极限条件下，在保证安全行车距离的同时实现跟车舒适性，设置舒适性减速度ac，并对其值进行约束。本车车速大于72 km/h时，减速度ac上限为3.5 m/s2；车速小于18 km/h时，减速度上限为5.0 m/s2；两车速之间，减速度线性变化，如图3所示。

图3 ac约束值

1.3 滑模控制算法设计

1.3.1 滑模面设计

滑动模态可以设计且与对象参数和扰动无关，能够快速响应，对参数变化和扰动性不灵敏，即鲁棒性较好，同时无需系统在线识别，物理实现简单。

跟车巡航控制中，在保证两车实际距离达到理想跟车距离的同时，后车车速也需要稳定快速跟随目标车速。设计滑模变结构控制算法，使距离偏差ζ和速度偏差vr都趋向于0[10]。根据这2个约束条件，设计滑模切换函数s为

s=ζ+λvr

(2)

λ为滑模切换面系数；s=0即为系统滑模切换面。距离偏差为

(3)

L为两车实际距离。两车速度偏差，即相对速度vr为

vr=vf-vx

(3)

根据这2个约束条件，获取后车跟车的理想加速度，实现车辆驱动扭矩和制动器的逆向控制。

1.3.2 趋近率设计

(4)

ε为等速系数；k为指数系数。将初步阶跃函数sgn(s)改进为包含阶跃函数的饱和函数sat(s)[11]。其表达式如式(5)所示，函数图像如图4所示。

(5)

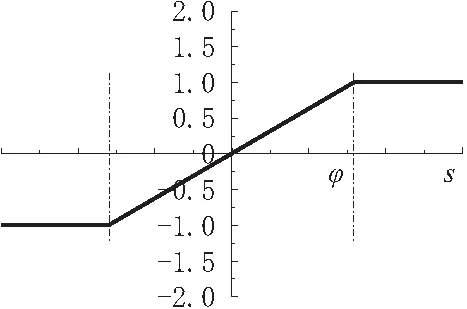
图4 饱和函数sat(s)

φ为变化区间值，由图4可知，状态在距滑模面的距离越来越小时，速度随之减小直至为0，有效缓解抖振。但线性过度不够平滑，为此将线性过度区域改为双曲正切函数，修改后的饱和函数如式(6)所示，图像如图5所示。

(6)

图5 饱和函数sato(s)

最终优化后的趋近率为

(7)

建立滑模控制方程，将式(2)与式(7)联立得

(8)

综上推导，后车跟车理想加速度ad为

(9)

1.4 发动机逆模型

需求加速度的计算最终转化为发动机的扭矩和制动力，并作为Carsim仿真软件的输入信号实现控车。根据汽车行驶运动力学分析，可得汽车行驶纵向方程式为

Ft=Ff+Fw+Fi+Fj

(10)

Ft为驱动力；Ff为滚阻助力；Fw为空气阻力；Fi为坡道阻力；Fj为加速阻力。假设汽车无转向且在平直无风道路行驶，式(10)可分解为

(11)

(12)

R为车轮半径；ig和ir分别为变速器和主减速器传动比；ηt为传动系统机械效率。

依据仿真工况中Carsim的发动机MAP图构造发动机逆模型，通过查表获得期望节气门开度。节气门开度的函数表达式为

αd=f-1(Teng,neng)

(13)

αd为目标节气门开度；Teng、neng分别为发动机扭矩与转速。

1.5 制动器数学模型

本车仿真制动器采用盘式制动器，通过理想加速度推导制动器压力，建立方程，可得

admReff=μbrAbrRbrPbr

(14)

Reff为有效轮胎制动半径；μbr为制动盘摩擦系数；Abr为制动盘接触面积；Rbr为制动盘制动力作用半径。添加响应滞后时间td，理想制动力Pbr为

(15)

1.6 节气门与制动器控制切换策略

本文采用车辆速度与加速度的关系设计发动机与制动器的工作门限曲线，并划分工作区间[12]。保证ACC自适应巡航控制车辆运动时，发动机与制动器工作不产生冲突。

利用Carsim软件，记录车辆在无节气门开度和制动压力的情况下，汽车带挡滑行的倒拖加速度ab。对曲线进行滤波处理，得到较为平缓的倒拖加速度曲线，即工作区域分界线，如图6所示。

图6 倒拖加速度曲线

当车辆加速度在曲线附近时，为防止发动机和制动器频繁切换，在曲线上下分别设置2个门限曲线，其与原曲线的距离为h=0.04 m/s2，两曲线之间为过渡层，改进后的切换曲线如图7所示。

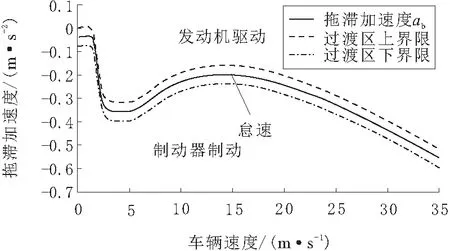
图7 带有过渡层的拖滞加速度

ACC巡航系统由决策层计算出目标加速度，一部分由发动机拖滞扭矩及传动系统摩擦产生的倒拖加速度抵消，因此发动机与制动器的工作切换策略如表1所示。

表1 加速度切换策略

2 仿真分析

在汽车仿真软件Carsim中建立仿真环境，添加车辆运动信息模块，设置本车初始速度和前车在不同工况下的速度。搭建Simulink仿真模型[13]，与Carsim联合仿真，形成闭环仿真系统。

2.1 加速度响应对比

根据实验数据对比[14]并调试发动机逆模型和制动器逆模型相关参数，使执行机构更符合真实响应状态。依托某汽车公司以PID实现ACC自适应巡航功能的量产车进行跟车实验，使用CAN工具与车身总线建立通信，实验设备及场景如图8所示。

图8 实验场景

将实验需求加速度作为仿真目标加速度，输出至执行器逆模型，同时联合Carsim获得仿真下的响应加速度，并与实验实际响应加速度对比，仿真结果如图9～图11所示。

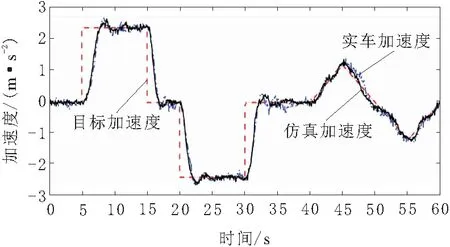
图9 实验与仿真的加速度对比

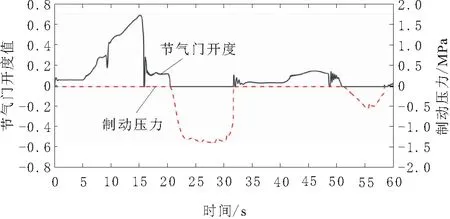
图10 节气门开度与制动力

图11 加速度偏差

实验车辆初始车速为30 km/h，目标加速度在-2.0 m/s2与2.0 m/s2的幅度下变化。因发动机与制动器切换策略，节气门与制动器转换处过渡平稳。节气门开度在稳定段波动幅度较小，在不稳定段略有震荡，制动器轮缸压力值较为平顺。由图11可知，仿真加速度与实验响应加速度的偏差基本保持在±0.2 m/s2以内，验证了下层执行系统的准确性与真实性。

设置仿真步长Ts，仿真参数如表2所示。

表2 仿真参数

2.2 目标车加速后匀速工况

设置目标车加速后匀速行驶工况，前车以由静止加速行驶，最终在达到60 km/h时匀速行驶，本车与前车初始距离为4.0 m，同样由静止开始跟车巡航。在Carsim建立相应工况环境进行仿真，记录仿真数据并与实验数据对比分析，两者数据对比如图12～图15所示。

图12 车速跟随

图13 加速度跟随

图14 理想车距跟随

图15 速度与距离偏差

由图12可知，前车在6.4 s开始加速，因系统迟滞，仿真车辆在其1.2 s左右后产生速度响应，较实验样车略快。在18.6 s和36.5 s左右，分别达到目标车的速度，时间上与实验车辆较吻合，且未产生超调，很好地完成了对目标车的速度跟随。

图13中，仿真样车实际加速度能够快速响应目标加速度，响应时间小于100 ms，且超调量较小。同时仿真目标加速度较实验目标加速度变化幅度小，加速度跟随稳定平缓，体现了滑模控制算法良好的鲁棒性。

图14中，依据理想跟车距离策略，前车车速大于本车车速时，目标跟车距离较小于实际跟车距离，加快了本车对前车速度的跟随，同时缩小车间距。结合图15中速度偏差，车辆达到稳态跟车巡航后，实际车速与前车车速间的误差小于最大限值2 km/h。距离偏差中，实际距离收敛至目标安全距离，偏差在1.5 m以内，符合设计要求。

2.3 高速下目标车加减速并停止工况

在跟车巡航中，前车变道切出后，根据传感器探测当前车道是否存在跟随目标，车辆完成定速巡航模式或新目标跟车巡航模式的切换。

设置目标车从60 km/h加速至100 km/h，随后减速至40 km/h，变道切出切入，最后减速直至停止。本车进行跟车巡航，定速巡航目标车速为110 km/h。仿真数据与实验数据进行比较，验证改进后的跟车功能在性能上的提升，如图16～图19所示。

图16 车速跟随

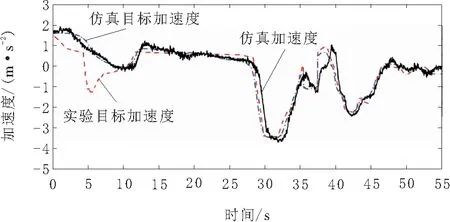
图17 加速度跟随

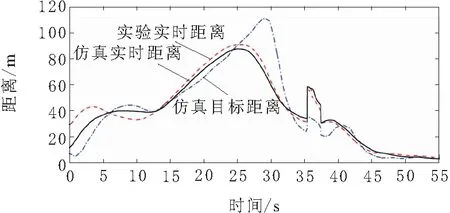
图18 理想车距跟随

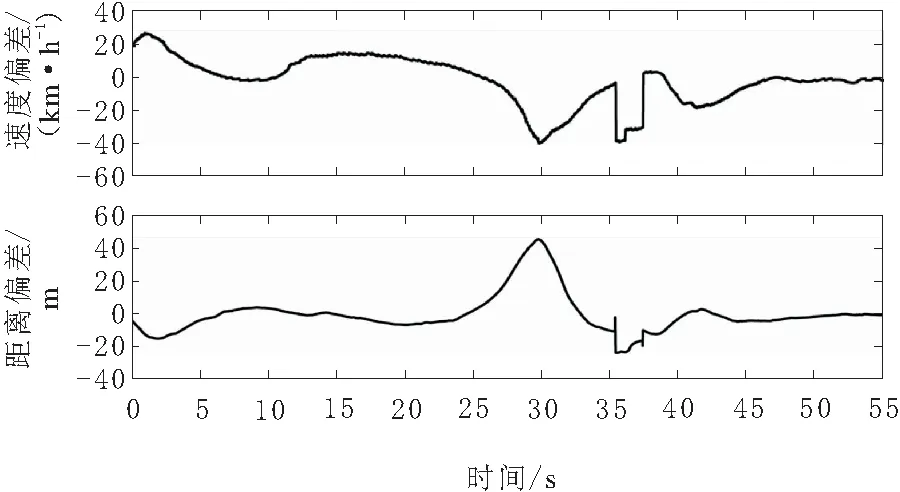
图19 速度与距离偏差

从10.0 s开始，实验样车与仿真样车同时跟随前车加速，由图16可知，仿真样车在27.5 s左右达到100 km/h，较实验样车快2.0 s。随后跟随前车急减速，在减速度段，依据跟车策略，仿真车辆车速略小于实验样车，保证了一定的安全性。在35.0 s处， 前车以40 km/h匀速切出本车道，2.0 s后以相同速度切入，两车都能够快速更新巡航目标，同时减慢车速降低碰撞风险。

图17中，加速阶段，仿真目标加速度由开始的较小值逐渐增大，与实车目标加速度相比，动态响应性更好。在急减速段，减速度未超过最大限值4.0 m/s2，仿真样车较实车减速度较大，因此速度较小于实验车辆，提高了跟车安全性。在加速度的约束下，保证了减速的舒适性。

图18中，当前车减速较大时，根据理想跟车策略，理想跟车距离急剧增大，使本车较快降速，防止碰撞。当目标车切入后，目标车车速高于本车车速，本车先加速再跟随前车减速直至停车。仿真样车跟停后与前车相距约2.8 m，与设计的跟停距离3.0 m相近。

根据图19可知，速度偏差和距离偏差在稳态跟车后都能够保证在相应约束条件中。本工况完成了在高速下的加速与急减速跟随，同时能够实现前车切入切出时的跟车巡航功能切换，并满足跟停。与实车控制策略相比，安全性略有提高。

3 结束语

本文以汽车自适应巡航控制系统中车辆跟车巡航速度控制为研究对象，设计了考虑制动距离和舒适性的理想可变车间据策略，同时对滑模控制算法进行改进，优化趋近率。仿真结果表明：设计的滑模控制算法能够很好地实现对前车速度和两车理想车间距的跟随，提高了跟随快速性及稳定性。并且通过对滑模趋近率的改进，有效减小了系统抖震，验证了算法的精确性和优越性；优化后的可变跟车距离策略在前车急减速的情况下后车能够舒适性减速，提高了车辆制动时的安全性和舒适性。