一种新型圆形掺杂光子晶体光纤负色散特性的分析
2023-02-14阮志强张磊赵欣瑜江兴方
阮志强, 张磊, 赵欣瑜, 江兴方
(常州大学微电子与控制工程学院, 江苏 常州 213164)
0 引 言
随着社会和互联网经济的发展,光纤通信已成为当今通信的主流。但是伴随着人们对信息传输速率和通信量要求的日益增高,限制光纤应用的两大难题(衰减和色散问题)也变得愈发尖锐,尤其是光纤密集型波分复用(DWDM)中的色散问题,极大地限制了光纤传输的容量。由于在同一介质中不同波长光波的传播速度不同,引起脉冲展宽而产生色散,DWDM 系统主要应用于波长1550 nm 处[1−3],需要利用色散补偿型光子晶体光纤(DCF)来进行色散补偿,从而改善传输效率。
近年来,很多研究人员研究了DWDM 中的色散问题。Maji 等[4]于2016 年设计了一种双芯的正方形包层的光子晶体光纤,发现其可在范围1400 ∼1600 nm 内实现有效的宽带色散补偿,色散系数可达到−2000 ps·nm−1·km−1左右;Zhang 等[5]为实现有效色散补偿,开创性地设计了正八边形的光子晶体光纤,其在传输波长1550 nm 处的负色散可以达到−1434.9 ps·nm−1·km−1左右。
本文运用有限元法对圆形结构的液体填充光子晶体光纤进行了色散补偿研究,针对波长1550 nm 窗口的色散补偿进行了详细的数值计算与模拟。
1 光纤结构与色散计算方法
本研究所设计的圆形双芯光子晶体光纤横截面结构如图1 所示,包层是分布在纯硅背景下的直径为d1的空气孔构成的圆形格点。从中心向外的第一层、第二层、第四层、第五层和第六层按圆形排列,旋转角度分别为60◦、30◦、14.4◦、12◦和10◦,Λ 表示空气孔层层间距,内芯为直径为d2的掺杂区,折射率nL= 1.753,外芯是移去第三层的空气孔的纯硅环。表征透明光学材料中随波长变化的折射率时通常采用Sellmeier 公式[6](也称为Sellmeier 方程或Sellmeier 色散公式),其典型的形式为
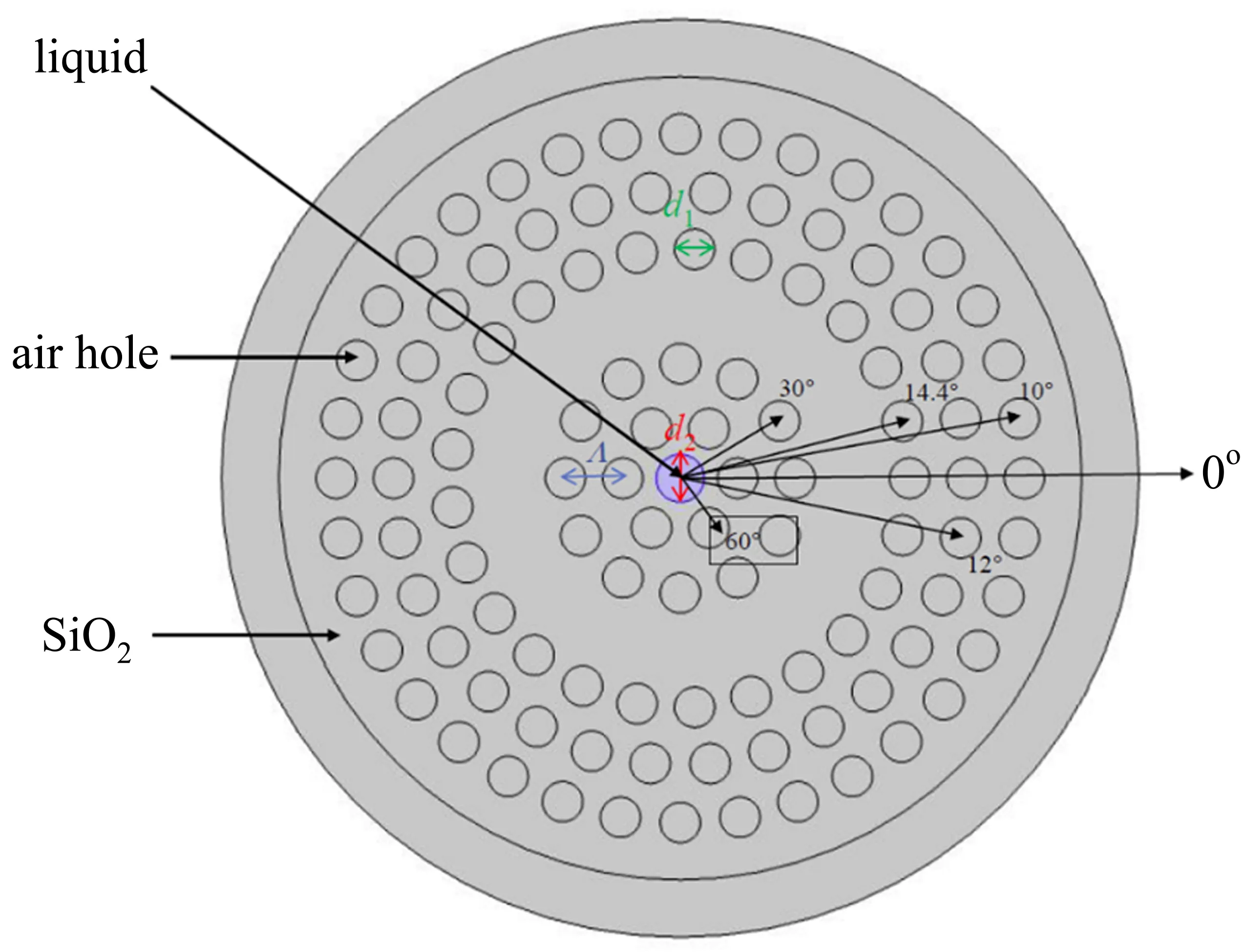
图1 圆形掺杂光子晶体光纤横截面Fig.1 Cross section of circular doped photonic crystal fiber

式中:n为折射率,λ 为波长,Bj和Cj为依据经验决定的Sellmeier 系数[7]。可以通过Sellmeier 公式计算出纯硅环的折射率为[7]

式中:B1、B2和B3分别为0.696166300、0.407942600 和0.897479400,C1、C2和C3分别为0.00467914826、0.0135120631 和97.9340025。
应用有限元数值分析方法[8−11],结合COMSOL Multiphysics 软件对所提出光子晶体光纤进行分析,只需要确定光纤的电磁参量和几何参量并输入对应波长,就能计算出光子晶体光纤的波导色散,可以表示为

式中:c为真空中的光速,λ 为工作波长,neff为有效折射率。光子晶体光纤的材料色散由Sellmeier 方程给出[6],总色散为材料色散和波导色散之和。
2 光纤的负色散特性及仿真分析
所设计双芯结构的光子晶体光纤之所以能产生负色散,是因为这种结构的光子晶体光纤支持两个超模,即基模和二阶模[12]。当工作波长小于某一波长λ0时,电场基本上集中在内芯传播,如图2(a)所示;当工作波长大于某一波长λ0时,电场主要集中在外芯传播,如图2(b)所示;而当工作波长在λ0附近时,电场在内芯与外芯之间都有分布,如图2(c)所示。这种传播现象使得光纤的有效折射率在λ0处发生转折,从而产生负色散。
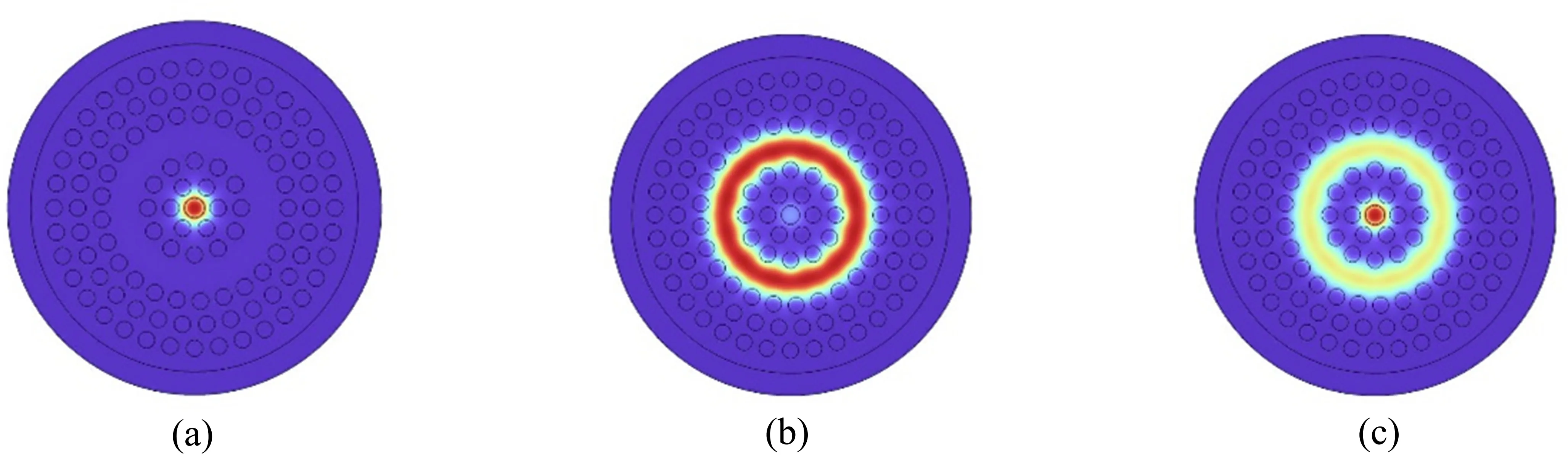
图2 三个传输区间的电场能量分布图。(a)耦合前;(b)耦合后;(c)耦合时Fig.2 Electric field energy distribution diagram of three transmission intervals. (a)Before coupling;(b)After coupling;(c)When coupling
2.1 空气孔直径d1 对色散的影响
固定空气孔层间距Λ=1550µm,固定中心孔直径d2(d2/Λ=0.833),中心掺杂液体折射率nL=1.753。改变空气孔直径d1与空气孔层间距Λ 的比值d1/Λ,可以得到有效折射率和波长的关系[图3(a)]以及色散与波长的关系[图3(b)]。由图3(a)可见:当Λ、d2和nL固定不变时,随着d1/Λ 的变小,有效折射率的最大变化率逐渐向长波长方向移动,这表明两区间的耦合波长值逐渐变大;由图3(b)可见:随着d1/Λ值的减小,色散的最小值向长波长区域移动,d1/Λ = 0.70 时在波长1550 nm 处可以得到约为−131960 ps·nm−1·km−1的大负色散值。
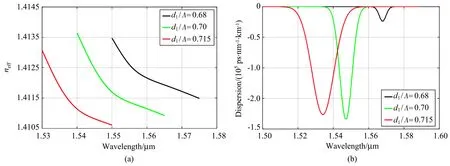
图3 改变空气孔直径得到的(a)有效折射率和(b)色散Fig.3 (a)Effective refractive index and(b)dispersion obtained by changing air hole diameter
2.2 中心孔直径d2 对色散的影响
固定空气孔层间距Λ = 1550µm,d1/Λ = 0.7,nL= 1.753。改变d2的大小,可以得到有效折射率与波长的关系[图4(a)]以及色散与波长的关系[图4(b)]。由图4(a)可见:当固定Λ、d1和nL,随着d2的变大,有效折射率的最大变化率逐渐向长波长方向移动,这说明两个传输区间的耦合波长值变大;由图4(b)可见,随着d2的变大,色散的最小值向长波长方向移动,d2/Λ = 0.833 时在波长1550 nm 处可以得到约为−132720 ps·nm−1·km−1的大负色散值。
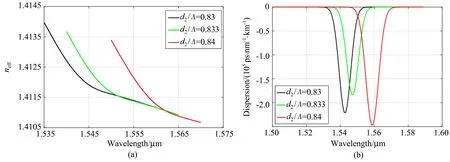
图4 改变中心孔直径得到的(a)有效折射率和(b)色散Fig.4 (a)Effective refractive index and(b)dispersion obtained by changing diameter of the central hole
2.3 中心掺杂液体折射率nL 对色散的影响
固定Λ = 1550µm,d1/Λ = 0.7,d2/Λ = 0.833,改变nL的大小可以得到有效折射率与波长的关系[图5(a)]以及色散与波长的关系[图5(b)]。由图5(a)可见:当固定Λ、d1和d2时,随着nL的增大,有效折射率的最大变化率逐渐向长波长方向移动,这说明两个传输区间的耦合波长值变大;由图5(b)可见:随着nL的增大,色散的最小值向长波长方向移动,nL= 1.753 时在波长1550 nm 处可以得到约为−131960 ps·nm−1·km−1的大负色散值。

图5 不同液体折射率对应的(a)有效折射率和(b)色散值Fig.5 (a)Effective refractive index and(b)dispersion corresponding to different liquid refractive index
3 结 论
设计了一种新型圆形掺杂双芯光子晶体光纤,采用有限元法并利用Comsol 软件研究其负色散特性。结果表明,通过调节光子晶体光纤的结构参数可以得到不同程度的大负色散值。固定层间距不动,随着空气孔直径的变小,色散最小值会逐渐向长波长方向移动;随着中心孔直径的变大,色散峰谷值会逐渐向长波长方向移动;当中心掺杂液体折射率逐渐变大时,色散峰谷值会向着长波长方向移动。并且当Λ = 1550µm、d1/Λ = 0.7、d2/Λ = 0.833 以及nL= 1.753,可得到−132720 ps·nm−1·km−1的高负色散值。可见,所设计的光子晶体光纤既能灵活地改变几何结构以便实际应用,又可以提供较大的负色散以用作色散补偿光纤。
