标记单光子源下探测器死时间的量子密钥分配
2023-02-14何业锋李丽娜白倩陈思昊强雨薇
何业锋, 李丽娜, 白倩, 陈思昊, 强雨薇
(1 西安邮电大学网络空间安全学院, 陕西 西安 710121;2 桂林电子科技大学广西密码学与信息安全重点实验室, 广西 桂林 541004)
0 引 言
量子密钥分配(QKD)[1]是量子通信的一个重要分支,其安全性主要依赖于量子力学基本原理而非传统密码学中的计算复杂度,具有绝对安全性。随着BB84 协议的提出[2],研究人员致力于研究使通信距离更远、密钥生成率更高的方案。在实际通信系统中由于光源和测量设备的不完美性而存在许多类型的攻击。例如,致盲攻击[3]、时移攻击[4]、伪态攻击[5]、光子数分离攻击[6]、波长攻击[7]和雪崩过渡区攻击[8]等。鉴于QKD 系统中的大多数攻击都是针对探测器漏洞的。2012年,Lo 等[9]提出了与测量设备无关的量子密钥分配(MDI-QKD)协议,有效地解决了针对探测器侧信道的攻击问题。随后,国内外研究人员对MDI-QKD 协议展开研究并取得了一系列成果[10−15]。
在实际的MDI-QKD 协议中,一般使用弱相干态(WCS)光源来代替理想单光子源。Wu 等[16]基于WCS 光源在MDI-QKD 协议中引入探测器品质因子作为实验模拟参量,得到了探测器品质因子和密钥生成率之间的关系。但由于WCS 光源中单光子脉冲所占比例较小,导致密钥生成率降低。Fasel 等[17]用标记单光子源(HSPS)来代替MDI-QKD 协议中的WCS 光源,因为HSPS 光源中的单光子脉冲占比相较WCS 光源中的更大,所以得到的密钥生成率更高。Zhu 等[18]将基于HSPS 光源的MDI-QKD 协议和诱骗态理论相结合,得到了安全密钥率和通信距离之间的关系。在诱骗态方案中,发送者除了要发送信号态之外,还要发送不同强度的诱骗态。诱骗态一般分为两种: 主动诱骗态和被动诱骗态。主动诱骗态是指Alice 需要主动制备诱骗态,被动诱骗态则不需要。Zhang 等[19]提出一种新的三强度诱骗态方案,该方案仅在X 基下制备诱骗态脉冲,同时采用了集体约束和联合参数估计技术,显著降低了量子误码率。Zhang 等[20]提出一种被动诱骗态的MDI-QKD 协议,利用内置的局部探测事件被动地产生不同的诱骗态。Zhou 等[21]探究了基于HSPS 光源的MDI-QKD 协议在通信者Alice 和Bob 探测效率取不同值时的安全密钥生成情况。
Rogers 等[22]提出随着光子传输速率的不断提高,探测器死时间的存在可能会影响安全密钥生成速率。Burenkov 等[23]进一步介绍了探测器死时间和主动窃听者存在的情况下改进的安全密钥筛选方案,并对这些安全筛选方案进行了分析和比较,最后计算和模拟了它们的安全密钥生成速率。
本文首先在考虑和不考虑探测器死时间两种情况下,对基于HSPS 光源的MDI-QKD 协议和基于WCS 光源的MDI-QKD 协议[24]的安全密钥生成速率进行了分析和比较;然后分析了探测器死时间τ=50,100,150 ns 时,基于HSPS 光源的MDI-QKD 协议的安全密钥速率生成曲线;最后,得出了安全密钥生成速率的极限值和探测器死时间之间的关系。
1 基本原理
HSPS 可以同时产生信号光子和闲频光子。由于这两种模式具有同步性,闲频光子可以用于精准地预测信号光子到达第三方Charlie 的时间和光子数。信号光子在完成编码后,由不可信的第三方Charlie对其进行贝尔态测量(BSM),其光子数服从泊松分布

式中:Pd和ηd分别表示探测器的计数率和探测效率,n为光子数。
基于HSPS 光源协议的模型如图1 所示,其中Alice 和Bob 为发送方,Charlie 为第三方,BS 为分束器、IM 为强度调制器、Pol-M 为偏振调制器、PBS 为偏振分束器。1H、2H、1V、2V 分别表示第三方Charlie 的单光子探测器。具体的协议步骤为:1)Alice 和Bob 基于指示单光子源分别制备一对纠缠光子,首先将闲频光子发送给触发探测器a 和b 进行探测,然后根据探测结果对信号光子到达第三方的时间进行预测;2)信号光子通过偏振调制器Pol-M 选取X 基或Z 基进行编码。经过IM 将光子随机调制成三种光子态强度:µi和νj(i,j=0,1,2),且µ2>µ1>µ0=0, ν2>ν1>ν0=0,其中µi、νj分别代表Alice 和Bob调制后的光强,0、1、2 分别对应各自的真空态、诱骗态和信号态;3)第三方Charlie 在接收到来自Alice和Bob 发送的信号光子后对其进行Bell 态测量,并在光子传输结束后公布他的测量结果。Alice 和Bob中任意一个再根据第三方Charlie 公布的测量结果进行比特翻转,得出初始的密钥,最后通过对初始密钥进行纠错和保密加强等处理得到最终的安全密钥。
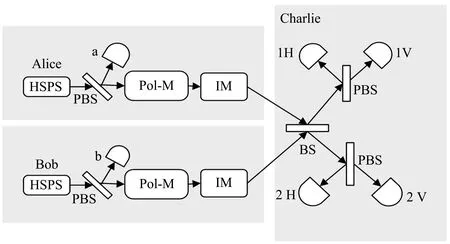
图1 基于HSPS 光源的MDI-QKD 协议模型Fig.1 MDI-QKD protocol model based on HSPS
2 密钥生成率分析
通信双方Alice 和Bob 通过基比对和隐私放大得到最终的安全密钥率[9]

当通信双方发送的信号脉冲强度分别为n、m时,总增益和误码率可以分别表示为

Alice 到Charlie 的距离记为LAC,Bob 到Charlie 的距离记为LBC。当LAC=LBC时,该信道被称为对称信道,系统传输效率为η=ηa= ηb=tηd,其中t= 10−αL/10为信道传输效率,α 为信道传输损耗率,ηd为探测效率。本研究中所使用的信道为对称信道,提及的协议均为MDI-QKD 协议。
3 高速MDI-QKD 与有限的探测器死时间
一般来说,安全密钥生成速率随着光子传输速率(单位时间内发送的光子脉冲数)的增大而增大。然而在实际的通信系统中存在探测器死时间,即当光子的传输速率过高时,探测器检测完一个单光子不能立刻进入检测下一个光子的状态,该时间间隔被称为探测器死时间[26]。如果此时窃听者在窃听密钥生成的过程中同时引入误码率,就可以获得一些关键信息,比如两个基下密钥的概率分布,这对安全密钥的生成会构成极大的威胁[24],引起较高的误码率。Rogers 等[22]分析了这个过程,提出了高效检测的想法并分析了高速QKD 协议的安全性。Burenkov 等[23]做了进一步分析,提出在考虑探测器死时间时,基于BB84协议的QKD 协议的有效检测概率为

式中:ηc=Qµ2ν2;k= ρτ,ρ 表示光子传输速率,τ 表示探测器死时间。在考虑探测器死时间的情况下,得到安全密钥生成速率的表达式
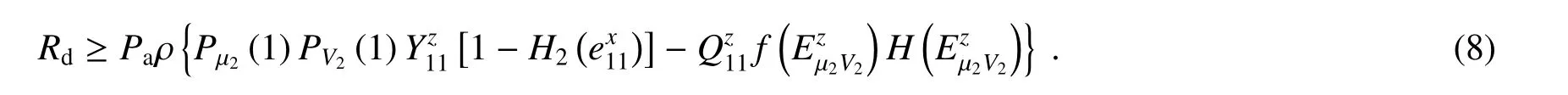
当光子在信道中传输的速率达到一个临界值时,恰好使得探测器死时间对系统产生影响,本研究将这一临界值称为光子传输速率临界值。将光子传输速率达到最大但对系统不会产生影响的值称为光子传输速率的最佳取值,即最优值。
4 仿真结果及分析
在分析光子传输速率和安全密钥生成速率之间的关系时,考虑脉冲为无限时的高速QKD 协议,即光子传输速率较高的情况。在仿真过程中,L= 100 km,µ1= 0.01, µ2= 0.36,Pd= 3×10−6, ηd= 0.9。将(1)、(5)、(6)、(7)式代入(8)式,令τ=100 ns、τ=0 ns,可以分别得到在考虑和不考虑探测器死时间两种情况下光子传输速率和安全密钥生成速率之间的关系,如图2 所示;将不同的τ 值代入(7)式,可以得到探测器死时间对安全密钥生成速率的影响,如图3 所示。
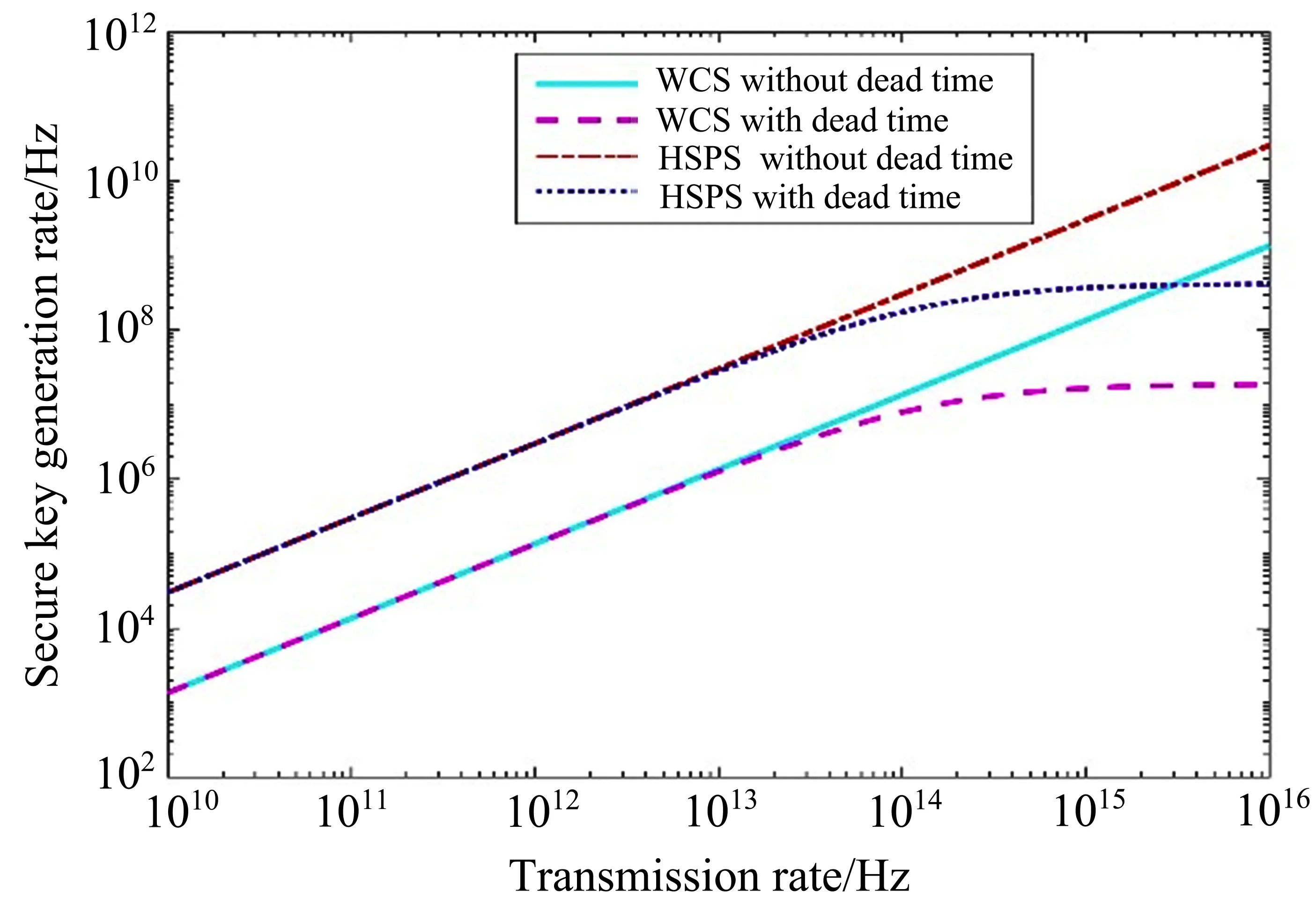
图2 不同协议下光子传输速率和安全密钥生成速率之间的关系Fig.2 Relationship between photon transmission rate and security key generation rate under different protocols
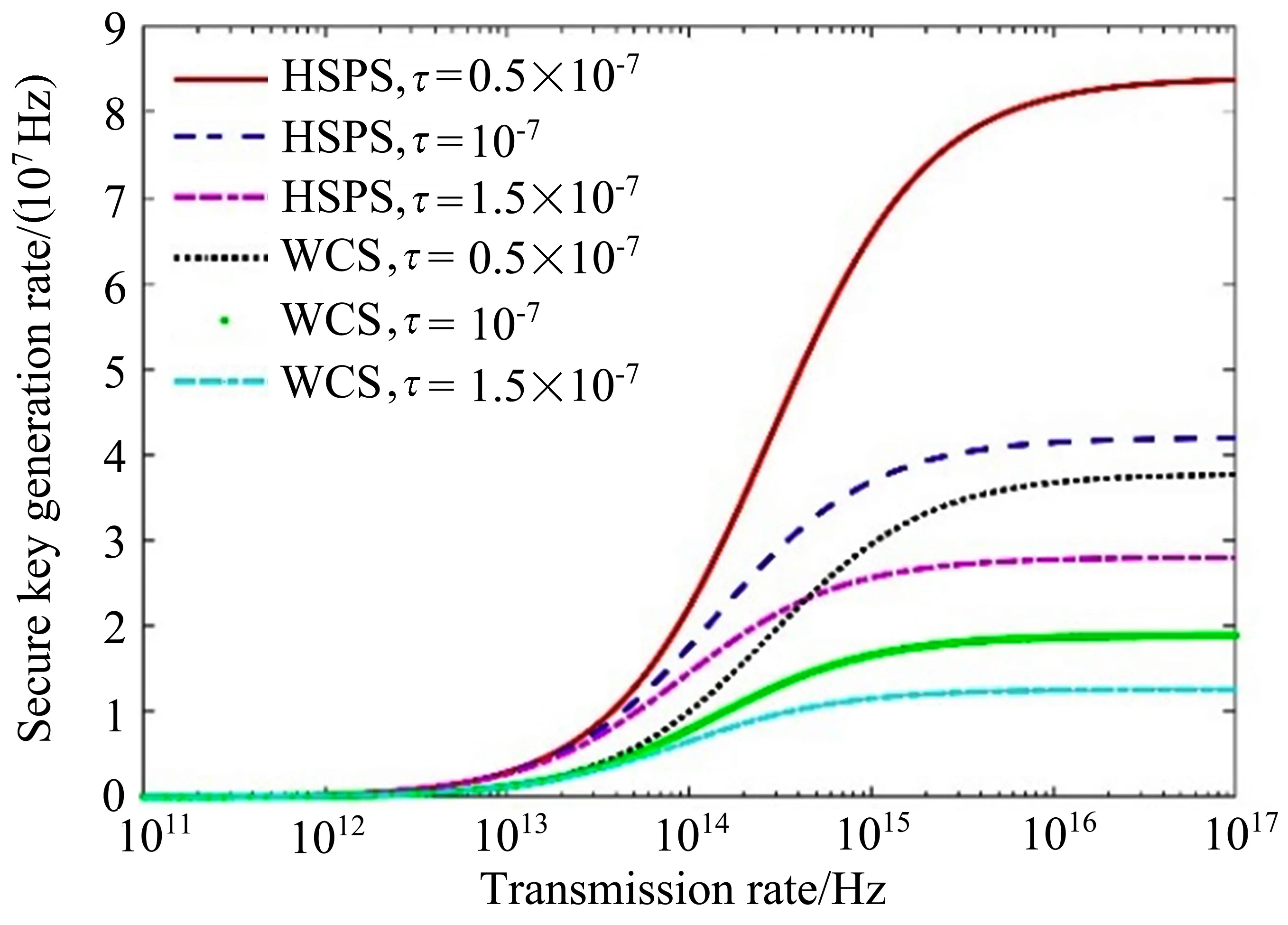
图3 探测器死时间取不同值时光子传输速率和安全密钥生成速率之间的关系Fig.3 Relationship between photon transmission rate and secure key generation rate under each detector’s dead time
5 结 论
在考虑和不考虑探测器死时间的情况下,探究了基于HSPS 光源协议探测器死时间对安全密钥生成速率的影响。结果表明:当光子传输速率过高时,探测器死时间的存在会对安全密钥生成速率产生影响。进一步比较了基于HSPS 和WCS 光源协议,在探测器死时间τ = 50,100,150 ns 时安全密钥生成速率的生成曲线。结果表明:在光源相同的情况下,探测器死时间越大,得到的安全密钥生成速率越低。在通信距离较远、触发探测器探测效率较高且探测器死时间相等的情况下,基于HSPS 光源协议的安全密钥生成速率要高于基于WCS 光源协议的。
