随机散斑图正交优化计算鬼成像

郭辉, 叶知秋

(阜阳师范大学信息工程学院, 安徽 阜阳 236037)

0 引 言

鬼成像(GI) 又被称为关联成像(CI), 是一种利用量子纠缠或光场涨落非局域获得物体图像的方法[1,2]。在成像过程中,散斑对目标物体进行连续照射,透射光或反射光经桶探测器测量并记录为没有空间分辨率的单像素强度序列,然后利用单像素强度序列与对应散斑的二阶关联运算对目标图像进行重构。2008 年,Shapiro[3]在理论上提出了计算鬼成像(CGI),利用空间光调制器调制激光预置热光场,代替以往光源制备中的旋转毛玻璃,将鬼成像的结构由原先的双臂简化为单臂。次年,Bromberg 等[4]利用计算机控制空间光调制器产生散斑图,完成了计算鬼成像实验,进一步提升了鬼成像的适用性。和传统成像方式相比,鬼成像具有不易被干扰、成像系统简单等优点,广泛应用于激光雷达探测[5]、光信息加密[6]、边缘检测[7,8]、运动物体检测[9]等领域,展现出十分广阔的应用前景[10,11]。

为改善鬼成像中目标物体的重构质量,研究人员提出了多种优化方案,如:针对光斑设计,人们设计制备了如正弦散斑图[12,13]、Hadamard 散斑图[14]等正交性散斑;针对鬼成像实验结构的改进,提出了差分鬼成像(DGI)[15]、归一化鬼成像(NGI)[16]等结构;根据图像原有的或在某种变换域下的稀疏性,将压缩感知引入鬼成像重构过程[17,18];随着数据量的急剧增长和计算机计算能力的快速提升,基于深度学习的鬼成像研究也取得了一系列研究成果[19−21]。这些研究在一定程度上促进了鬼成像的发展,但是针对随机散斑图模式下的计算鬼成像依旧存在成像质量差或算法比较复杂的问题。

针对随机散斑图计算鬼成像的成像效果问题,本文在原有计算鬼成像基础上,结合随机散斑图的协方差矩阵分析影响鬼成像中目标重构质量的因素,构造基矩阵将原有的随机散斑图通过矩阵映射为正交模式,使用重构的散斑图对目标物体进行照射,完成计算鬼成像目标重构过程。再结合重构散斑图协方差矩阵的对角线元素对重构结果进行补偿优化,从而提升重构物体质量,最后通过仿真验证了该方法的有效性。

1 随机散斑图正交优化计算鬼成像方案

图1 为随机散斑图正交优化计算鬼成像原理图,其中传统随机散斑图Ri(x,y),i= 1,2,··· ,N经正交优化后得散斑图R′j(x,y),j=1,2,··· ,N。重构散斑图由数字微镜器件(DMD)调制后对目标物体进行照射并由桶探测器测量得到一系列桶探测器值B′j,i= 1,2,··· ,N,将计算机记录的重构散斑图与对应桶探测器值进行二阶关联运算以获取目标图像,结合重构散斑图协方差矩阵对重构图像进行补偿优化。

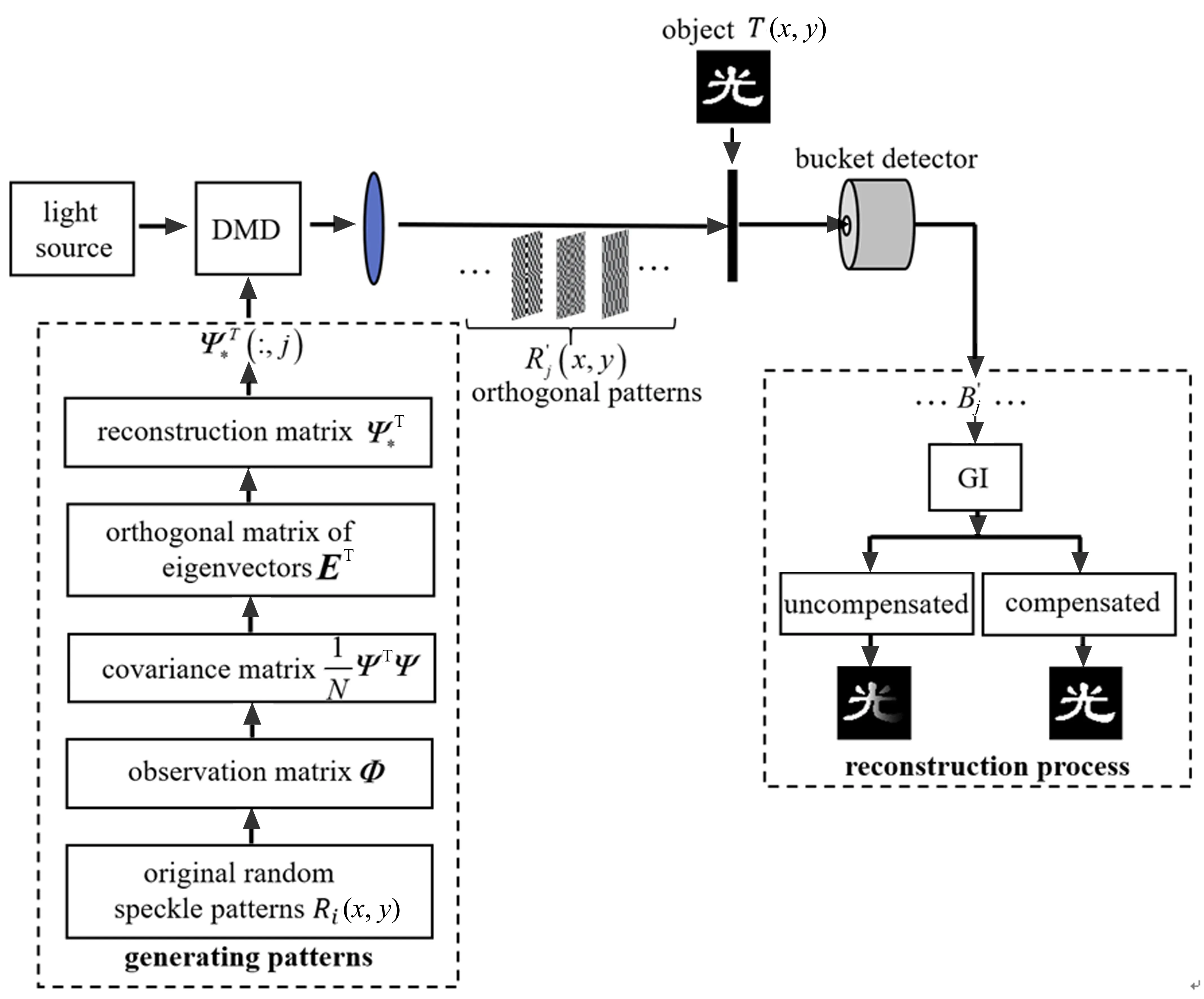
图1 随机散斑图正交优化计算鬼成像原理图Fig.1 Schematic diagram of orthogonal optimization of random speckle patterns for computational ghost imaging

传统计算鬼成像中,光源照射计算机控制的DMD 产生一系列随机散斑图Ri(x,y),i= 1,2,··· ,N,通过透镜聚焦在目标物体T(x,y) 后, 透射光由不具有空间分辨能力的桶探测器接收并记为Bi,i=1,2,··· ,N。该过程可表示为

为进一步了解影响计算鬼成像物体重构质量的因素, 假设目标物体的透射尺寸为p×q像素, 则T(x,y)可以表示为T=[T(1,1)T(1,2)···T(p,q)]T。由(1)式可知,随机散斑图对目标物体的N次照射,可以构造一个N×K(K=p×q)的观测矩阵Φ,表示为[22]

由(5)式可知当A为一个对角线矩阵,并且对角线上的元素相同、非对角线值为0 时,可有效重构待测物体。由矩阵相关理论可知,对称正定矩阵A与对角矩阵Λ 满足

由(5)、(10)式可知,与原随机散斑图的协方差矩阵A相比,重构散斑图的协方差矩阵A∗由噪声干扰项构成的非对角线元素显著降低,因此重构散斑图具有更好的目标重构效果。此时对角线秩的衰减会导致重构图像的亮度衰减,将重构图像与向量[1/(λ1+k) ··· 1/(λN−1+k) 1/(λN+k)]点乘,对重构图像进行补偿,进而提升目标物体重构质量,其中k为非零常量。

2 数值仿真与结果对比

为客观准确地说明随机散斑图正交优化计算鬼成像的性能,引入峰值信噪比(PSNR,RPSN)[18],可表示为式中a(x,y)和b(x,y)分别代表原始图像数据和恢复后的图像数据,图像大小为m×n。

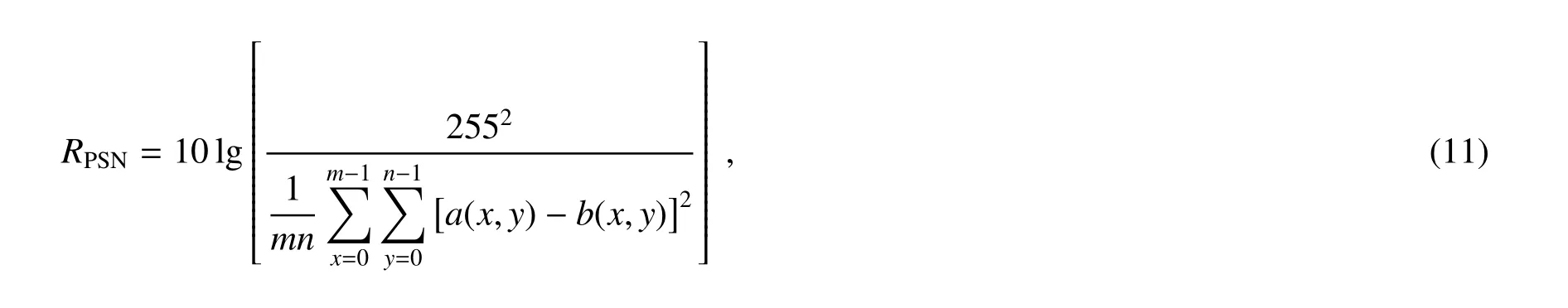
实验仿真平台为Windows10,CPU 为Core i7-8700K,软件为MatlabR2018a。数值仿真中,通过计算机构造64 pixel×64 pixel 的标准正态分布随机数矩阵来模拟实验中的随机散斑图。通过4096 次光斑照射,得到4096 pixel×4096 pixel 的随机散斑图矩阵。原随机散斑图的协方差矩阵如图2(a)所示,对随机散斑图进行正交优化后得到的重构散斑图的协方差矩阵如图2(b)所示。由图2(b)可以看出,相比于图2(a),重构散斑图的协方差矩阵非对角线上的噪声明显降低。虽然影响目标物体重构质量的协方差矩阵对角线元素存在一定的衰减,但是可以通过补偿提升所述方法的目标重构质量。

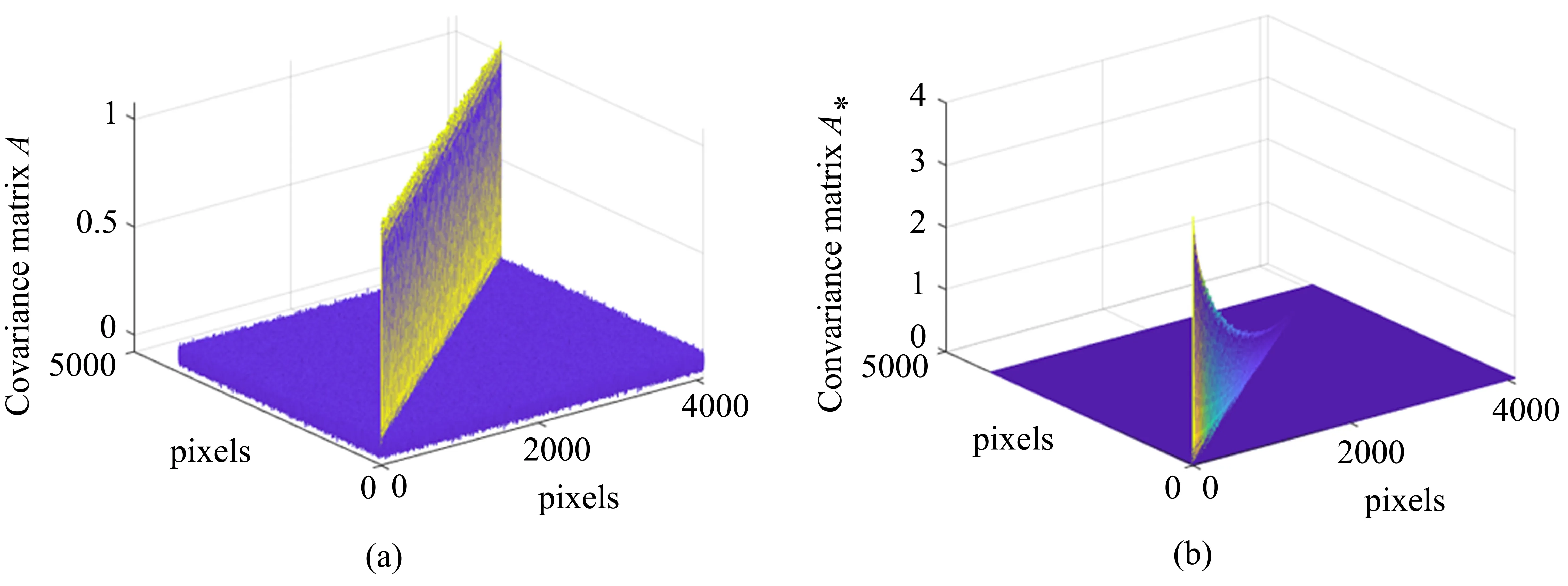
图2 散斑图协方差矩阵。(a)原始随机散斑图协方差矩阵A;(b)重构散斑协方差矩阵A∗Fig.2 Covariance matrix of speckle patterns. (a)Covariance matrix A of original random speckle patterns;(b)Covariance matrix A∗of reconstructed speckle patterns

为证明本方案的有效性, 选取64 pixel × 64 pixel 的五幅图像作为目标物体, 即三幅二值图像“光(Guang)”图、“NUPT”图、“鬼(Ghost)”图及两幅灰度图像即“Lena”图、“Cameraman”图,如图3(a)所示。图3(b)∼(d)分别为随机散斑图计算鬼成像、本研究所提方法(未补偿)、本研究所提方法(补偿)在4096 次散斑图照射下目标图像的重构效果,其中补偿向量中的参数k值为0.0002。由图3 可以看出相对于随机散斑图计算鬼成像,本研究所提方法无论在未补偿状态还是补偿状态下,均能有效降低散斑图的统计噪声对目标物体重构质量的影响,从而增强重构目标物体的清晰度。本研究所提方法在未补偿状态下,由于重构散斑图协方差矩阵对角线的衰减,使得重构物体左侧亮度高于右侧亮度。对于二值物体,若目标物体集中于观察区域的左侧,则对目标物体的识别影响较小;对于灰度物体,由于重构散斑图协方差矩阵对角线的衰减,使得重构图像丧失部分细节信息,但总体视觉效果依然优于随机散斑图计算鬼成像的重构结果。由图3(d)可知,与图3(c)相比,本研究所提方法在补偿状态下能够弥补重构物体的亮度衰减问题,具有良好的成像效果。

为定量评价随机散斑图计算鬼成像、本研究所提方法未补偿和补偿情况下的性能,参考(11)式计算重构图像相对于目标图像的RPSN,如表1 所示。由表1 数据可知,在未补偿状态下本研究所提出方法二值图像的RPSN比随机散斑图计算鬼成像的高,灰度图像的RPSN略低于随机散斑图计算鬼成像的重构结果。由图3(a)可以看出二值图像存在大量没有细节的区域,本研究所提出方法在未补偿状态下重构物体的亮度衰减对主信息的识别影响不大,而对于灰度物体右侧存在大量图像信息的情况,亮度衰减对目标物体重构质量的影响较大。表1 中的数值结果与图3(c)中重构图像的视觉效果相吻合。结合表1 数据可知,本研究所提出方法在补偿状态下对二值、灰度图像重构结果的RPSN与随机散斑图计算鬼成像相比均有明显提升,说明了本研究所提方法的有效性。

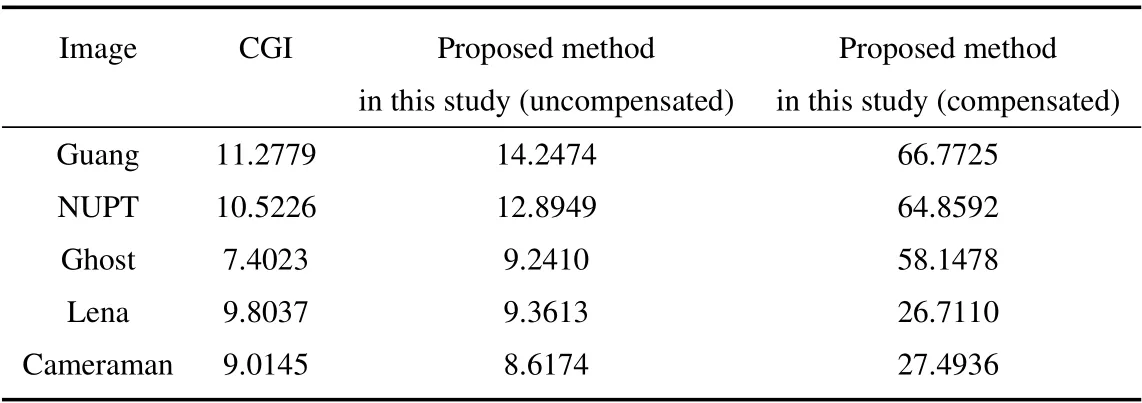
表1 CGI、本研究所提出方法未补偿和补偿下重构结果的RPSN (dB)Table 1 RPSN (dB)of reconstruction results of CGI,the proposed method(uncompensated)and the proposed method(compensated)in this study

图3 不同方法的重构结果。(a)原始物体;(b)CGI 重构结果;(c)本研究所提方法重构结果(未补偿);(d)本研究所提方法重构结果(补偿)Fig.3 Reconstruction results of different schemes. (a)Original images;(b)Reconstruction results of CGI;(c)Reconstruction results of the proposed method in this study(uncompensated);(d)Reconstruction results of the proposed method in this study(compensated)

鬼成像实验过程中,桶探测器数据采集往往存在一定的噪声,为进一步探究本研究所提出方法的有效性,在桶探测器的测量过程中引入加性高斯白噪声,研究RPSN−BD与图像重构质量的关系,其中RPSN−BD满足

式中:PS为桶探测器所探测的实际信号能量值,PN为噪声能量值。

分别以二值图像“光(Guang)”图、灰度图“Lena”为目标物体,考虑所使用的照射散斑图为随机散斑,各种方法均对目标物体做10 次重构测量并取RPSN的平均值,得桶探测器加入白噪声后目标成像质量的仿真曲线,如图4 所示。图4(a)为二进制图像“光(Guang)”不同RPSN−BD下各方法的RPSN效果图,由图4(a)可以看出随着桶探测器噪声的增大,所有方法的RPSN都在不断衰减。本研究所提出方法(补偿)对噪声敏感度较高,但在一定的噪声范围内,无论本研究所提出方法在补偿还是未补偿情况下均具有优于随机散斑图计算鬼成像的目标重构效果。图4(b)为灰度图“Lena”不同RPSN−BD下各方法RPSN的效果图,由图4(b)可知,各方法的RPSN在桶探测器噪声增大的情况下不断衰减。随机散斑图计算鬼成像的目标重构质量优于本研究所提出方法在未补偿条件下的结果,但低于本研究所提出方法在补偿条件下的结果,这与图3 和表1 中的结果相一致。综合图4(a)与图4(b)可知,虽然噪声对本研究所提出方法(无论在补偿状态还是未补偿状态)均有一定程度的影响,但在一定噪声大小范围内本研究所提出方法具有优越性。

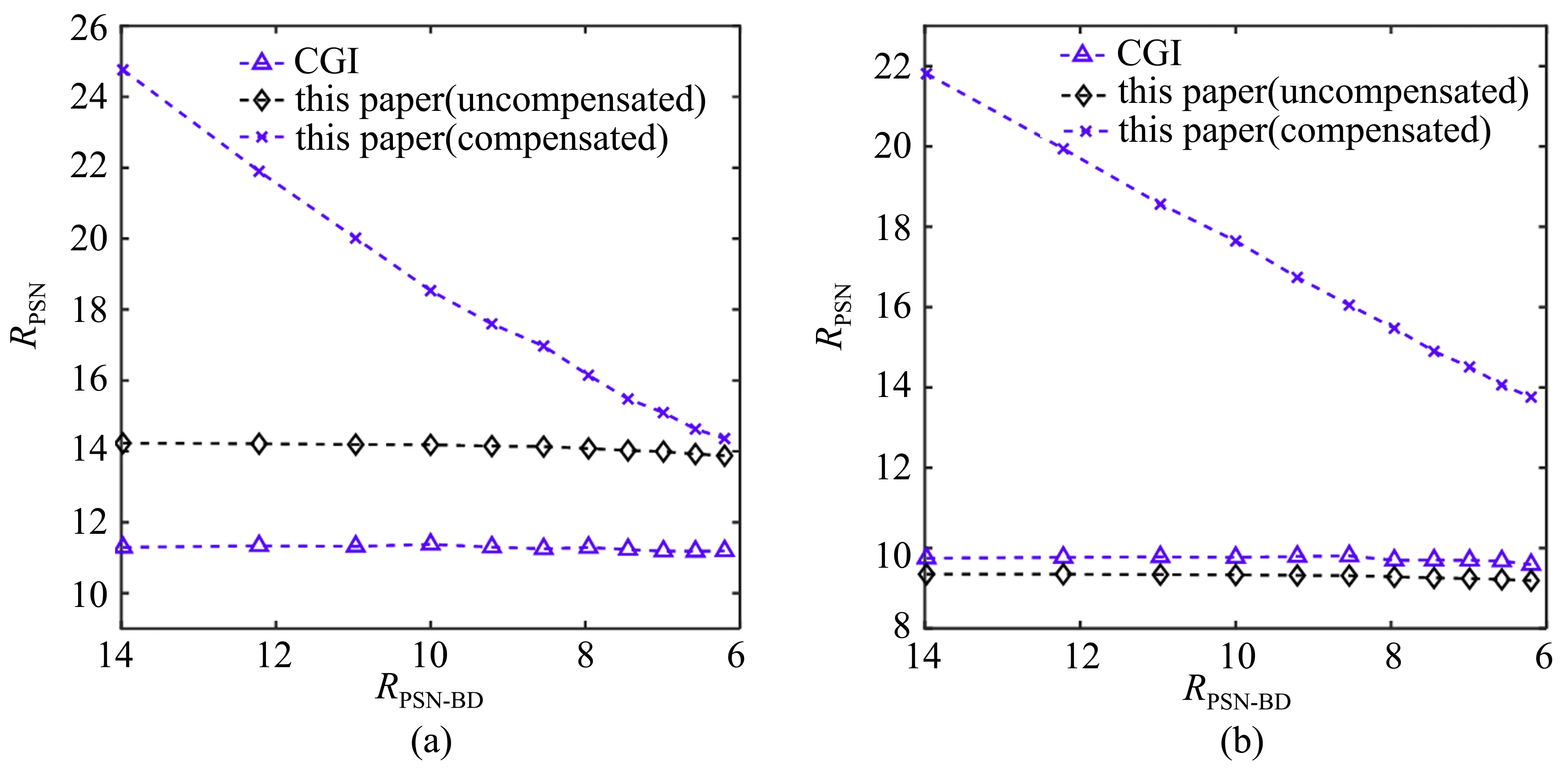
图4 不同方法下RPSN 相对RPSN−BD 的性能曲线。(a)目标对象为“光(Guang)”图;(b)目标对象为“Lena”图Fig.4 Curve of RPSN performance against RPSN−BD under different schemes. (a)The target object is picture“Guang”;(b)The target object is picture“Lena”

3 结 论

针对随机散斑图,提出了一种随机散斑图正交优化计算鬼成像方法,并将多组二值图像和灰度图像作为待测物体,采用不同方法进行重构比较,进而向桶探测器加入白噪声,对比研究不同方法下的RPSN相对RPSN−BD的性能曲线。理论分析及仿真实验都验证了本研究所提出的方法在改善随机散斑图计算鬼成像成像质量方面的有效性,与传统鬼成像方法相比,所提出的方法克服了散斑图矩阵的非正交性引入的相关性噪声,提高了成像质量。