基于PSO-SVR算法的工业机器人分级标定方法

薛祥儒，张承瑞+，胡天亮，陈齐志，丁信忠

(1.山东大学 机械工程学院,山东 济南 250061；2.上海新时达机器人有限公司，上海 201802)

0 引言

随着机器人离线编程技术应用越来越广泛，机器人的绝对定位精度成为评估机器人性能的重要指标之一[1-3]。标定技术可以通过软件算法提高机器人的定位精度，而无需改变其机械结构或设计，标定技术的经济性和有效性成为了提高机器人定位精度的有效方法。机器人的定位误差主要分为两类：①由几何参数因素引起的误差，包括关节角偏差、连杆长度偏差、连杆偏移误差、以及扭角偏差，该类误差大约占总定位误差的80%[4]；②非几何参数因素引起的误差，如关节柔性、连杆柔性、齿轮间隙以及摩擦等[5]。目前大多数研究都集中在基于运动学的几何参数误差的校准。

建模、测量、参数辨识和补偿是机器人结构参数标定的4个步骤。在建模方面，HARTENBER等提出了D-H模型[6]，但是当相邻两关节的轴线平行或者接近平行时，该模型不满足连续性。为了克服这些缺点，HAYATI等[7]提出一种修正的D-H(Modified D-H, MD-H)模型，通过增加一项绕y轴旋转的角度β，来解决相邻关节平行或接近平行时出现的奇异性问题。针对几何参数误差模型，陈绵鹏等[8]在建立时加入了减速比和耦合比误差，通过LM算法辨识出误差模型中的误差参数并补偿。陈宵燕等[9]建立了一种包含几何与柔性误差的完整刚柔耦合位置误差模型,并采用改进的LM算法进行求解。洪鹏等[10]提出一种利用空间网格来处理几何参数的误差模型，利用改进的LM迭代最小二乘法求出各网格对应的参数误差。但是，这些方法在求解过程中都没有考虑非几何参数因素对定位精度的影响。

针对齿轮间隙、摩擦、热效应等非几何误差因素问题，田威等[11]通过建立关节回差和减速比的误差模型，提出一种考虑关节回差的工业机器人误差相似度精度补偿方法。焦嘉琛等[12]提出一种分级补偿策略，通过耦合重力参数的运动学误差模型和空间网格的机器人刚度辨识方法来进行分级补偿。但是，以上方法对于非几何参数误差的考虑并不全面。因此，神经网络算法以及一些混合算法也被应用到非几何参数误差辨识补偿中来。花芳芳等[13]基于深度神经网络建立机器人误差模型，进而实现对误差的预测和补偿；WANG等[14]采用基于甲虫群优化算法的多层感知器神经网络(Multi-Layer Perceptron Neural Network, MLPNN)补偿非几何参数引起的残留误差；NGUYEN等[15]使用人工神经网络(Artificial Neural Network, ANN)来补偿由非几何误差源引起的机器人位置误差；GAO等[16]提出一种采用BP神经网络(Back Propagation Neural Network, BPNN)和粒子群优化(Particle Swarm Optimization, PSO)算法的新型混合算法，该算法运行过程中具有较少的迭代次数和更快的收敛速度。但是，神经网络算法在应用到小样本的数据建模及预测中容易出现过拟合的现象。相对于神经网络算法，支持向量回归机(Support Vector Regression, SVR)是基于统计理论的监督学习分类方法，具有坚实的理论基础，并且在小样本回归预测应用中能展现出较好的泛化能力[17-19]。

针对现有机器人标定过程中参数辨识以及误差补偿方法的不足，本文提出一种分级标定方法。首先，建立基于机器人MD-H模型和减速比、耦合比的运动学误差模型，采用LM算法辨识机器人的几何参数误差以及减速比、耦合比误差并计算得到残余误差。之后，将几何参数补偿后的残余误差输入到基于PSO-SVR算法建立的误差预测模型中，实现对非几何参数误差的预测和补偿。最后，通过激光跟踪仪和六自由度工业机器人来进行标定实验并验证提出方法的有效性。

1 机器人运动学模型

以六自由度工业机器人为研究对象，对机器人进行运动学标定，建立机器人运动学模型和误差模型。

1.1 机器人MD-H运动学建模

机器人的运动学模型是运动学参数标定的基础，由于MOTOMAN ES165D六自由度工业机器人关节2和关节3平行，运用D-H法建模存在缺陷，因此根据HAYATI等[7]提出的MD-H模型，建立机器人的坐标系，如图1所示。

根据建立的坐标系，机器人的MD-H参数表如表1所示。表中：连杆长度ai-1是沿Xi-1轴，将Zi-1移动到Zi的距离；连杆扭转角αi-1是沿Xi-1轴，将Zi-1旋转到Zi的距离；连杆偏置di是沿Zi轴，将Xi-1移动到Xi的距离；关节角θi是沿Zi轴，将Xi-1旋转到Xi的距离；βi表示相邻两轴绕y轴的旋转角度。

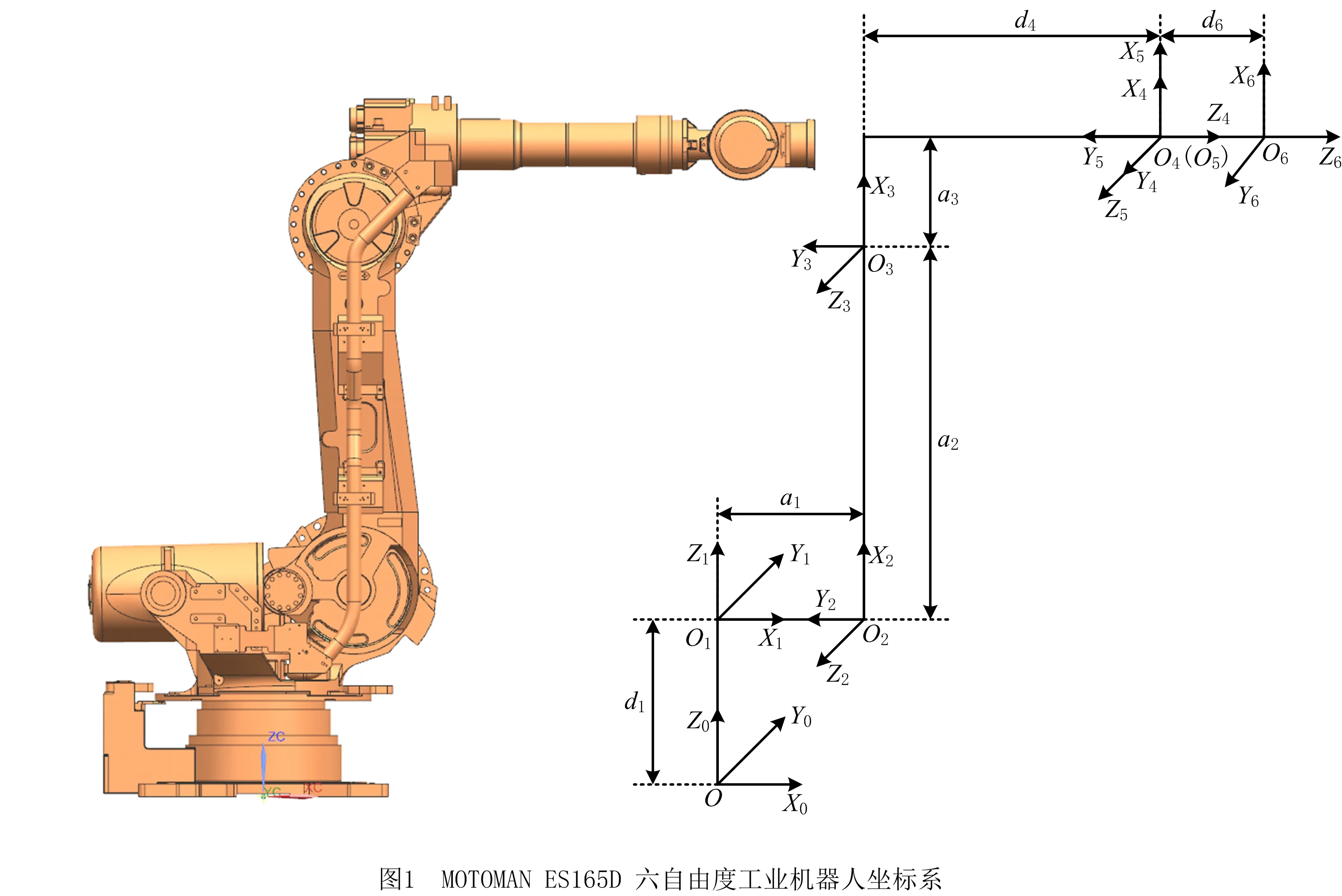
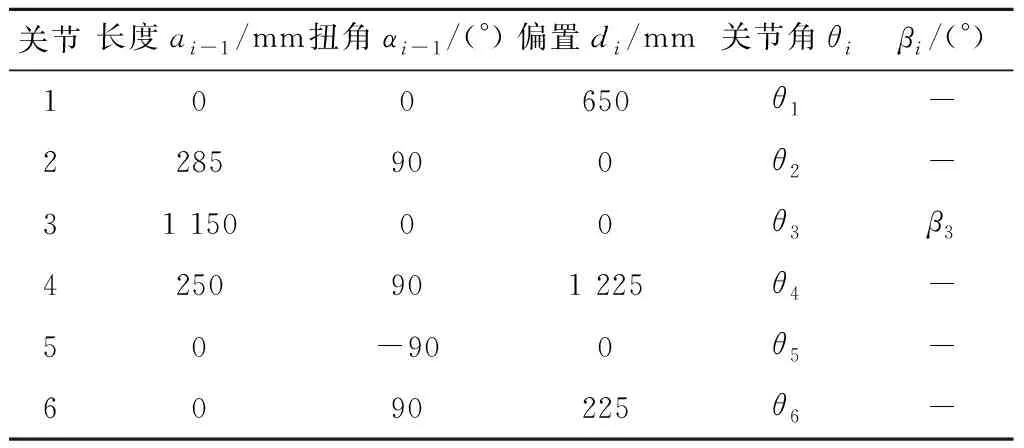
表1 MOTOMAN ES165D六自由度工业机器人MD-H参数表

根据空间坐标转换原理，相邻两个坐标系i-1和i的坐标转换方程可以用齐次变换矩阵的乘积形式来描述：

Tran(z,di)Rot(y,βi)。

(1)

展开即可得到相邻坐标变换方程的通用公式:

(2)

其中：cθi=cosθi，sθi=sinθi，式中其余情况以此类推。

对于n自由度的关节机器人，机器人运动学模型为：

(3)

1.2 减速比及耦合比建模

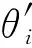
(4)

当两者没有误差时，ki=1。

由于机器人特殊的结构设计，出现跨关节的驱动布局，n轴的驱动路径超出n-1～n轴之间，就会出现耦合现象。对MOTOMAN ES165D六自由度工业机器人来说，5、6轴的电机并非固定到4、5轴结构件，而是安装在3轴结构件上，然后再通过传动机构传到5、6轴，这就导致机器人4、5、6轴之间存在耦合关系。当机器人4轴转动时，会造成5、6轴转动一定比例的角度，同时5轴转动时，也会导致6轴转动一定的角度，在标定过程中需要对该角度进行补偿。对于存在耦合的部分，同时考虑减速比的影响，机器人第5、6轴的指令角度和实际角度之间的关系为[8]：

(5)

(6)

式中rij表示第i轴和第j轴之间的耦合比。

1.3 几何参数误差建模

机器人末端位置误差可以用激光跟踪仪测得的机器人实际末端位置Pc与根据机器人模型求得的名义位置Pn之间的差值来表示，即

ΔP=Pc-Pn。

(7)

其中ΔP=(ΔPx,ΔPy,ΔPz)T。

考虑到Δθi，Δαi，Δai，Δdi，Δβ3，Δki以及Δr这些几何参数误差足够小，可以利用微分运动学模型来近似代替误差方程，即对运动学方程进行全微分处理，机器人末端的位置误差可以近似表示为：

(8)

在测量过程中，激光跟踪仪靶球的中心位置并不与机器人第6轴坐标系的原点位置重合，可以将靶球中心位置看作工具坐标系中心位置，即靶球的中心位置为机器人运动学方程右乘一个平移变换矩阵，即

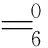
(9)

将式(8)写成矩阵形式即为：

ΔP=JδΔδ。

(10)

其中Jδ是一个3×34型矩阵，称为误差系数矩阵，即

Jδ=(Jθ,Jα,Ja,Jd,Jβ,Jk,Jr);

Δδ是一个由需要辨识的几何参数误差组成的34×1的矢量，即Δδ=(Δθ1,…,Δθ6,Δα0,…,Δα5,Δa0,…,Δa5,Δd1,…,Δd6,Δβ3,Δk1,…,Δk6,Δr45,Δr46,Δr56)。

2 几何参数误差辨识

在式(10)中，ΔP和Jδ都是可以通过测量和计算得出的已知量，因此34个几何参数误差Δδ求解问题就变成了求解矛盾方程组的问题。当方程组的数目大于几何参数的数目时，就可以用相应的辨识算法来求出各个参数的误差值。每一个测量点可以列出3个方程，则求解34个参数最少需要测量12个标定点，为了保证辨识算法的准确度，通常测量点的数量远大于最低需求点的数量。

(11)

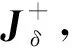
(12)

式中：μ为阻尼系数，μ>0；I为单位矩阵。

迭代过程中，LM算法通过调整μ值的大小来控制计算精度，使几何参数误差不断接近准确值。当μ较大时，算法接近梯度下降法，发挥全局特性，保证全局收敛;当μ较小时，算法接近Gauss-Newton法，发挥局部收敛。具体的参数辨识流程图如图2所示。

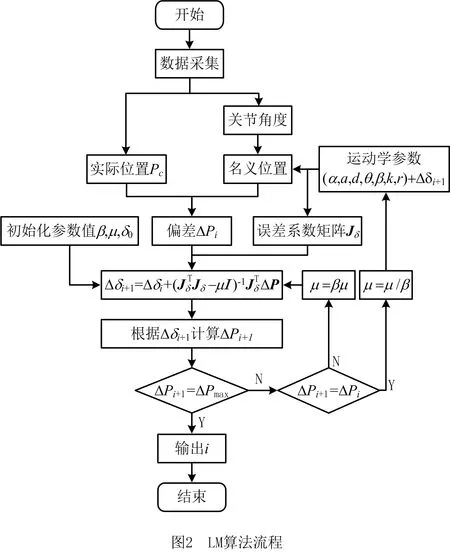
3 基于PSO-SVR的非几何参数误差模型建立及补偿

几何参数误差辨识并补偿后，机器人还存在较大的位置残余误差，该残余误差是由非几何参数误差引起，其误差模型构建存在难度。文中采用PSO-SVR混合算法来解决这个问题，通过SVR算法建立模型来预测机器人末端的非几何参数误差，同时采用PSO算法来优化SVR算法的参数取值，提高SVR算法建立的预测模型的准确度。

SVR拟合样本数据集{xi,yi}(i=1,2,…,n;xi∈Rd;yi∈R)，得到的回归函数为：

K(xi,x)+b*。

(13)

(14)

在SVR算法训练模型过程中，惩罚因子C、核函数系数γ和不敏感损失系数ε是影响SVR模型寻优能力的主要因素。惩罚系数C主要影响模型的复杂性和稳定性。不敏感损失系数ε主要控制回归函数对样本数据的不敏感区域的宽度，ε过大，容易导致学习精度不够；ε过小，容易导致模型过于复杂，甚至出现过拟合现象。核函数系数γ主要影响支持向量之间的相关程度。

经验法和试凑法是目前应用于这3个参数选取最多的方式，为方便可靠地找到最优参数组合(C,γ，ε)，本文选用PSO算法进行参数寻优操作。

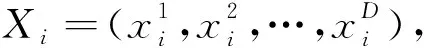
(15)

(16)

式中：i=1,2,…,m；d=1,2,…,D；r1和r2为(0，1)间的随机数;c1和c2为加速因子，取值范围大于等于0，主要作用为表征个体最优粒子以及全局最优粒子对当前粒子的影响;ω为惯性权重因子，表示上一次迭代搜索速度对下一次迭代搜索速度的影响程度，较大的ω有利于避免出现局部最优情况，较小的ω有利于提高粒子的区域搜索精度。为加快收敛速度，文中对ω值的选取采用自适应的方法，

(17)

式中：ωmax,ωmin为最大和最小惯性权重因子，取值为0.9和0.4；N为粒子群算法当前迭代次数；Nmax为粒子群算法总的迭代次数。

基于PSO算法对SVR算法中参数(C,γ，ε)进行优化，构建了PSO-SVR的混合优化算法，该算法的寻优步骤如下：

步骤1归一化处理要进行SVR模型训练的数据，并将数据分为训练集和检验集两部分。

步骤2确定粒子群算法参数。种群规模m，最大进化代数Nmax，最大、最小权重因子ωmax、ωmin，以及学习因子c1,c2。

步骤3随机初始化粒子群算法的初始种群。

步骤4计算当前粒子群各粒子的适应度。建立SVR模型，输入训练参数(C,γ，ε)，使用检验集数据检验训练的模型，并生成检验集的均方误差(MSE)，根据MSE计算出适应度值。

步骤5根据各个粒子适应度值的大小，更新个体最优粒子pi和全局最优粒子pg。

步骤6根据式(15)和式(16)进行迭代计算，更新粒子的位置、速度。

步骤7判断是否到达最大迭代次数，或者是否满足收敛条件，若达到最大迭代次数或者满足收敛条件则停止迭代，否则返回步骤4。

PSO优化SVR算法参数流程如图3所示。

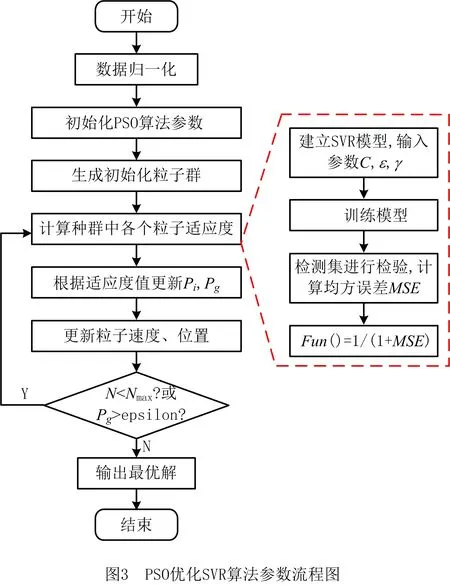
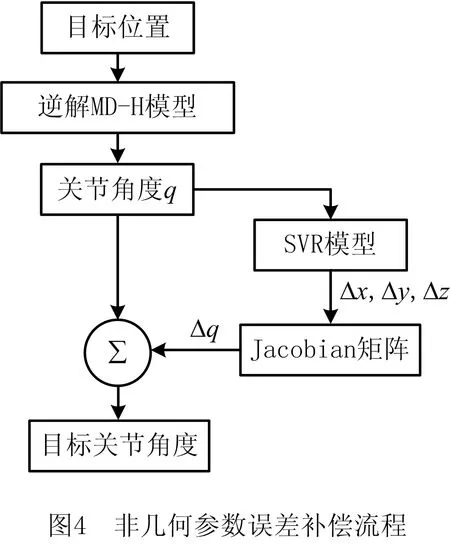
对于非几何参数误差补偿，将机器人关节角度输入到SVR预测模型中，该预测模型会输出机器人末端的定位误差。通过使用雅可比矩阵，将机器人末端的位置误差映射成关节角度误差，进而和逆解得到的关节角度q进行求和，得到目标关节角度。补偿过程如图4所示。

4 机器人标定实验

为了验证文中所述标定方法对六自由度串联工业机器人的绝对定位精度的标定效果，利用安川的MOTOMAN ES165D六自由度工业机器人和API公司的RADIAN Core型激光跟踪仪进行标定实验和精度验证试验，表2和表3分别为MOTOMAN ES165D六自由度工业机器人关键参数以及各关节运动范围参数，表4为API激光跟踪仪实验参数。激光跟踪仪的静态测量误差为10 μm+5 ppm(5 μm/m)，坐标重复性优于2.5 ppm，在实验过程中测量仪器和机器人位置的距离为1 m～3 m，则空间测量点的测量误差处在0.015 mm到0.025 mm之间，满足测量精度要求。

表2 机器人关键参数

表3 机器人各关节运动范围参数

表4 激光跟踪仪实验参数

激光跟踪仪的接收靶球固定在机器人的末端，以靶球的中心点作为机器人工具中心点(Tool Center Point, TCP)。在开始测量之前，需要将激光跟踪仪的测量坐标系转换到机器人基坐标系下，之后的所有测量数据都基于机器人的基坐标系，图5所示为试验现场。

在对SVR算法模型进行训练时需要用到大量的数据，为了进一步提高算法的准确度，应尽可能地增加测量点的数量。均匀地取分布在机器人工作空间内的630个点进行测量，图6为标定过程中测量的630个标定点。机器人控制器记录每个测量点对应的6个关节角度值，之后通过机器人正运动学计算出对应的笛卡尔名义位置坐标Pn，激光跟踪仪记录的每个测量点的三维坐标值作为机器人的实际位置Pc。在已知名义位置Pn和实际位置Pc的情况下，可以根据式(7)求得机器人末端位置误差ΔP。

4.1 几何参数误差辨识

为了验证辨识的效果，将所有的测量点分成两部分：一部分作为辨识点来辨识几何参数误差，另一部分作为检验点，只用来检验辨识效果。在630个测量点中随机选取500个作为辨识点，用来进行几何参数误差的辨识，剩下的130个测量点作为检验点。将500个点对应的机器人关节角度值以及实际位置Pc数据带入到LM算法中，利用算法程序迭代计算出辨识结果如表5所示。

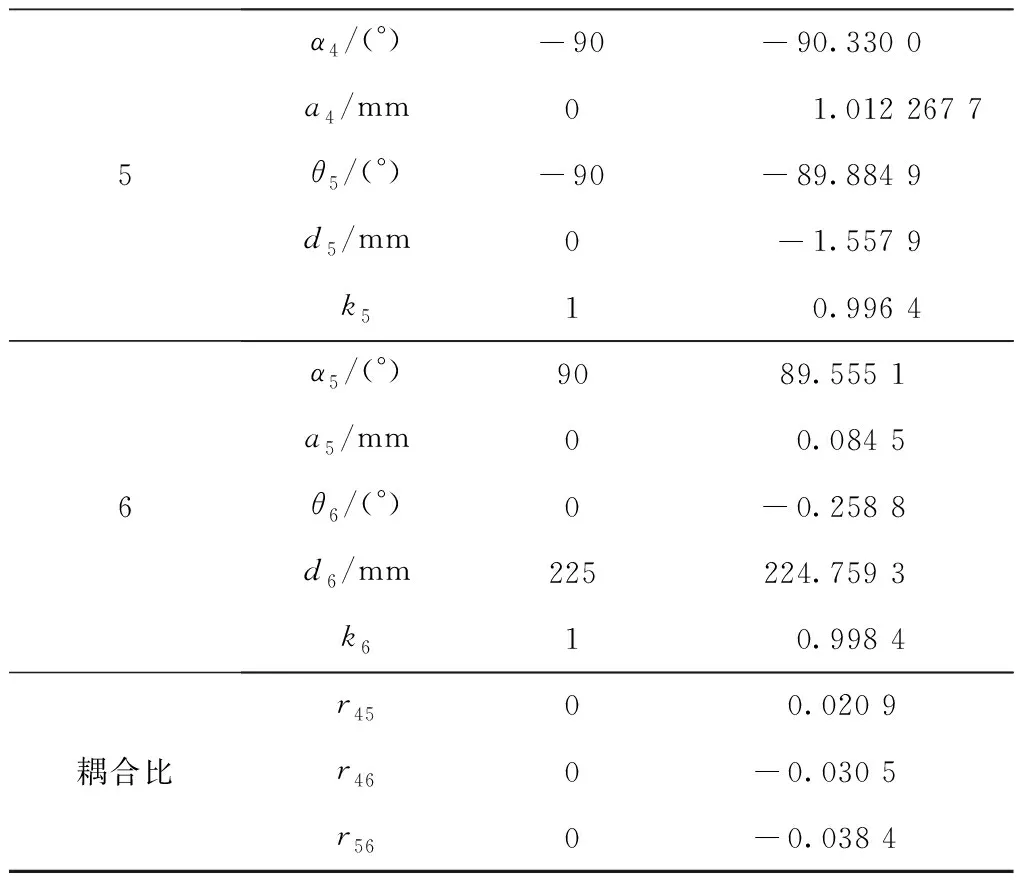
续表5

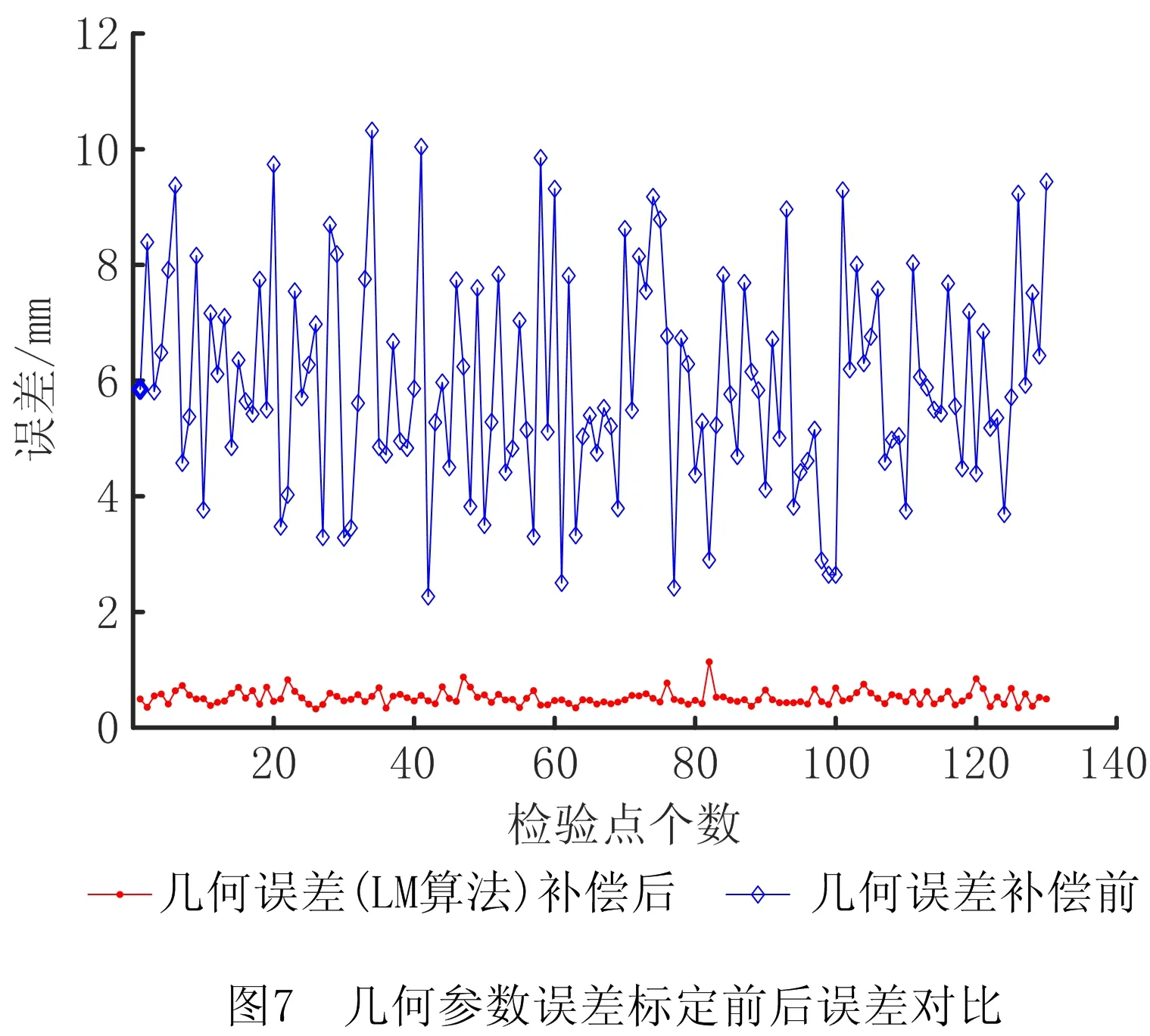
根据LM算法辨识得到的几何参数误差、减速比误差以及耦合比误差来修正理论模型，通过计算修正模型求出的130个检验点的理论位置和激光跟踪仪测量的实际位置的差值来检验几何参数标定效果，检验点误差如图7所示。经过几何参数误差辨识后，机器人的平均绝对定位精度相对于标定前的5.866 mm提高到了0.514 5 mm，有非常显著的提升。但是，标定后的误差依旧较大，存在进一步优化的必要性。

4.2 非几何参数误差辨识

在PSO算法对SVR参数优化的过程中，通过调节PSO算法的参数，可以最大可能地发挥优化能力。最终的参数设置如下：种群最大数量m=80，最大进化代数Nmax=100，学习因子c1=1.5,c2=2。另外，在PSO算法对SVR参数寻优的过程中，可以适当降低训练数据集在总数据集里的比例，来减少算法的优化时间，实验优化过程中的训练数据集占总数据集的比例为0.3。最终迭代寻优的适应度曲线如图8所示，PSO算法优化得到的SVR算法最优参数组合为：

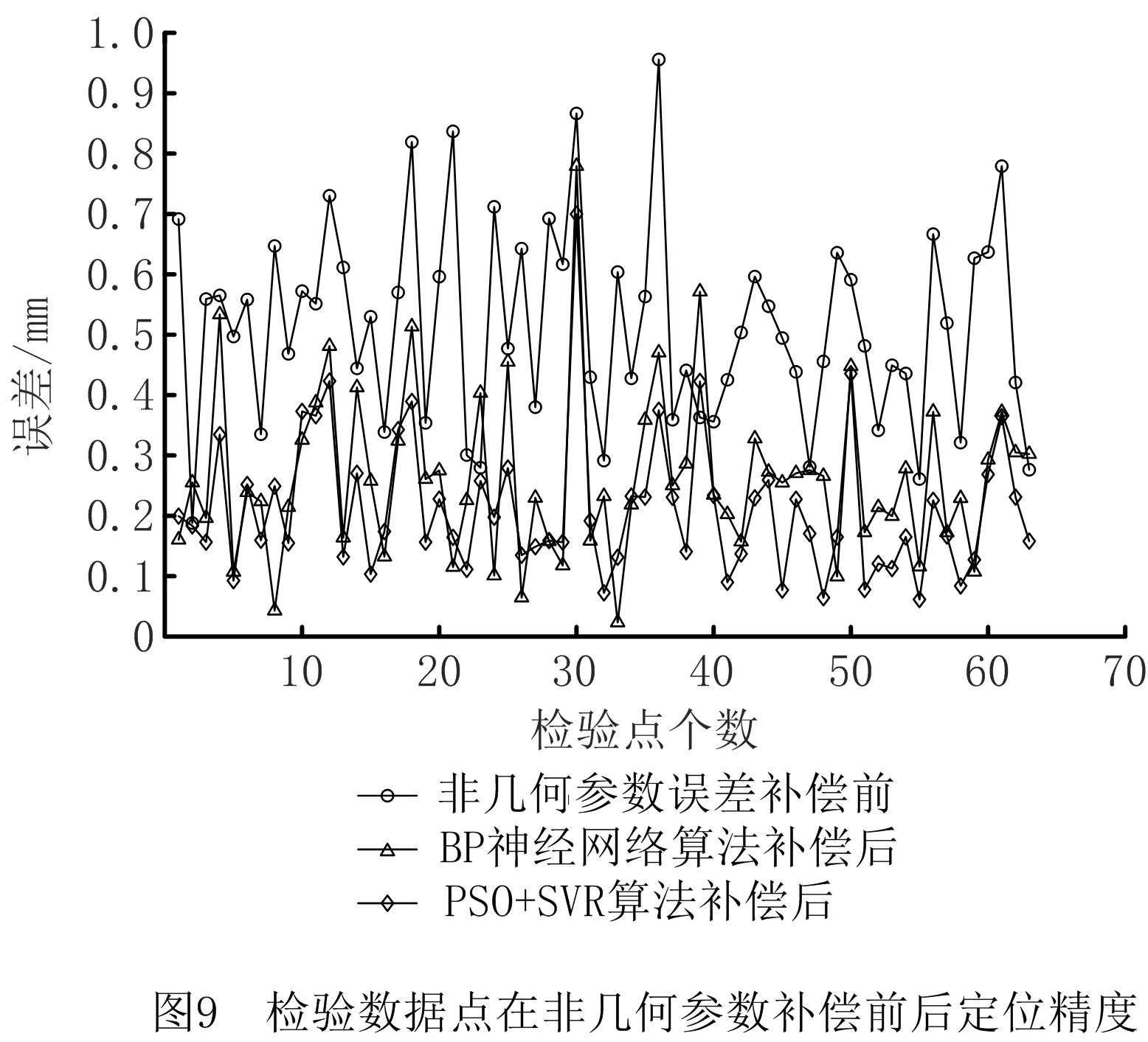
将PSO算法优化得到的惩罚因子C和核函数参数γ带入SVR预测模型，在模型训练过程中，从总数据集中随机选择567组数据作为训练数据，剩余的63组数据作为检验数据进行模型的验证，其中，检验数据不参与模型训练，来保证检验结果的有效性。另外，为了突出本模型的准确性，同时以相同的数据采用BP神经网络(BPNN)算法来训练模型。之后将两种算法得到的训练模型分别对机器人的非几何参数误差进行预测和补偿，并将补偿后的结果进行对比，如图9所示为检验数据点在非几何参数补偿前后的定位精度，从图中可以看出，PSO-SVR算法和BP神经网络两种方法相对补偿前都有着较为明显的精度提升，但是，PSO-SVR算法补偿后的机器人绝对定位精度相对于BP神经网络算法补偿后的精度提升更加明显，补偿结果也更趋于稳定。

为了对两种模型的补偿能力进行量化分析，选取误差平均值Mean、误差标准差Std以及误差最大值Max作为评价指标，各个指标参数值如表6所示。从表6可以看出，在相同的训练数据输入的情况下，PSO-SVR误差预测模型的平均绝对误差Mean=0.211 6mm、最大绝对误差Max=0.699 9mm和标准差Std=0.115 2mm都小于BPNN模型，误差平均值较小表明了PSO-SVR误差预测模型具有更高的准确度，最大误差和标准差较小主要体现了PSO-SVR误差预测模型具有更高的稳定性，表明PSO-SVR算法在面对小样本模型，处理过拟合问题上有更优秀的表现，验证了该算法的准确性和稳定性。

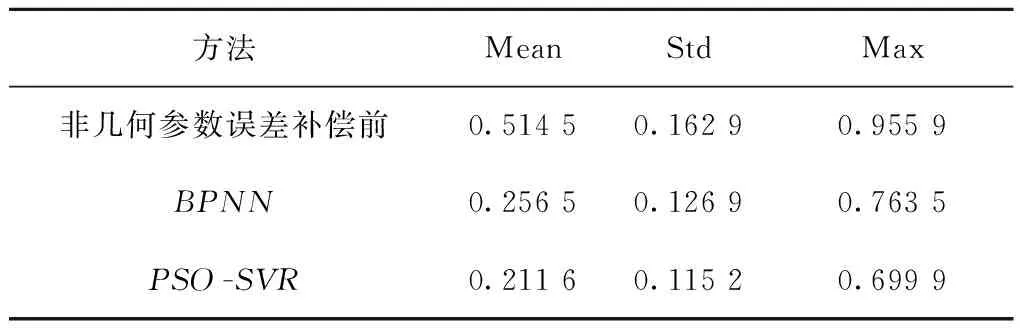
表6 两种模型性能评价指标量 mm

5 结束语

本文通过对六自由度工业机器人标定过程中几何误差和非几何误差模型的研究，提出一种分级的机器人标定方法。该方法通过两阶段的参数辨识和补偿：第一阶段建立了完整的工业机器人几何参数误差模型，采用LM算法实现了几何参数误差及传动误差的辨识；针对几何参数修正后的残余误差；第二阶段建立了基于PSO-SVR算法的残余误差预测模型，该模型综合考虑了非几何因素引起的残余误差，最后实现了工业机器人末端定位误差的高精度补偿。最后，开展了一系列工业机器人位置误差及标定实验，实验结果表明本文提出的方法能够准确辨识出工业机器人几何参数误差，同时提出的残余误差预测及补偿方法能够进一步提高工业机器人的绝对定位精度，经过分级标定后机器人末端中心点的平均位置误差由5.866mm减少到0.211 6mm，最大位置误差由10.322 9mm减少到0.699 9mm。文章主要分析和补偿了定位精度的位置误差，未来可以进一步将末端姿态的误差分析加入其中，从而进行全面的误差分析和补偿。