复杂动态环境下基于深度强化学习的AGV避障方法

蔡 泽，胡耀光，闻敬谦，张立祥

(北京理工大学 工业与智能系统工程研究所，北京 100081)

0 引言

自动导引车(Automated Guided Vehicle, AGV)因其自动化程度高、应用灵活等特点逐渐成为智能工厂物料运输的关键设备。在智能工厂中，工厂布局柔性多变、多AGV运行相互影响，使得AGV的运行环境更加复杂，对其动态避障能力有了更高的要求。

AGV避障路径规划要求AGV以合理的方式躲避障碍，安全高效地完成运输任务。早期的避障路径规划多采用集中式方法，由一个中央服务器决定所有AGV的运行，中央服务器可以获取工厂环境信息和所有AGV的运行状态，为多AGV同时规划无碰撞的路径[1]。集中式方法可以保证多个AGV安全运行，并能使路径达到近似最优，但这种方法严重依赖于实时通信和精准的状态感知，抗干扰和容错能力很差，不适用于复杂环境和有人参与的场景。与集中式方法对应的是分散式方法，分散式方法允许AGV只感知自身局部环境信息，不需要中央服务器。分散式方法中一种经典的方法是速度障碍法[2]，根据周围环境中障碍物的信息选择回避障碍的速度，基于此框架衍生出互惠速度障碍法(Reciprocal Velocity Obstacles, RVO)[3]、最优互惠速度障碍法(Optimal Reciprocal Collision Avoidance, ORCA)[4]等方法，但速度障碍避障方法需要对障碍的位置、速度和形状有精确感知，在现实应用中很难实现。

机器学习、大数据等人工智能技术的发展为AGV避障问题提供了新的解决方案，深度学习强大的表示能力与强化学习技术的结合，允许直接利用原始的传感器数据动态规划路径[5]。基于深度强化学习技术的避障方法通常采用端到端的模式，以传感器(如激光雷达、深度相机等)采集到的数据为输入，输出AGV的控制指令(速度、角速度、电机转速等)[6]，因为控制指令多为连续值，所以采用基于策略的算法[7]等。避障路径规划通常被设置为点到点的局部避障，AGV检测到障碍后从全局路径中选取一个路点作为局部目标点，无碰撞的运行到此目标点后视为避障结束[8]。避障过程被建立为适合强化学习解决的离散序列决策问题，在每个时刻根据环境的状态决策出运动控制指令[9]。基于以上模式，研究者开始探索在复杂环境中的避障方法。ZHU等[10]针对复杂室内场景(如迷宫等)中局部目标点难以定位的问题，将感知的第一人称环境图像作为输入，引导AGV运行；LONG等[11]针对多AGV场景下算法难以收敛的问题，提出多场景多阶段的训练方法，从简单到复杂的训练避障策略；CHEN等[12]考虑到人运动的随机性，融合多传感器评估行人意图，使AGV适应不确定运行环境。上述方法将局部避障视为点到点过程，以AGV是否到达目标点一定范围内作为避障结束的依据，该方式只关注了躲避障碍而没有考虑局部避障规划对后续运行的影响，避障结束后需要继续调整轨迹使AGV回到全局路径，影响了AGV的运行效率。

因此，为解决复杂动态环境下考虑全局路径引导的避障问题，本文提出一种基于深度强化学习的AGV局部避障路径规划方法。首先，将AGV避障问题表示为部分观测马尔可夫决策过程，详细介绍了观测空间、动作空间和奖励函数，在建立避障决策模型时同时考虑了路点位置和后续路径方向的引导作用；基于建立的决策过程，开发仿真环境并采用深度确定性策略梯度算法(Deep Deterministic Policy Gradient，DDPG)训练避障策略。最后，进行仿真实验，设置多种实验场景验证提出方法的有效性。

1 AGV避障问题描述与数学表征

1.1 问题描述与假设

在智能工厂中，设备布局柔性多变、多AGV同时执行物料搬运任务，AGV的运行环境更加复杂，为了安全、高效地执行任务，AGV需要有自感知与自决策能力。在运行过程中，AGV通过安装的传感器实时探测周围环境，当检测到附近存在障碍物时，需要自主规划出避障路径规避碰撞风险[13]；为完成搬运任务AGV通常采用全局与局部相结合的路径规划方法，在执行任务前先全局规划出从起点到任务目标点的全局路径，在运行过程中遇到障碍时进行局部路径规划。因此，局部避障路径规划既要满足无碰撞的要求，也要考虑任务的影响，在全局路径的引导下完成避障。在多AGV同时运行时，AGV需要躲避不同速度的障碍，因此局部避障路径规划需要具有应对动态环境的能力。

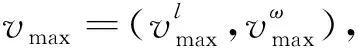
1.2 避障过程数学表征

局部避障路径规划可以表示为在等间隔离散时间点的序列决策问题，AGV上安装有感知周围环境的激光雷达，在开始时刻Ts(记时刻t=0)检测到有障碍物进入安全范围，AGV进入避障状态，从全局路径的路点中选择局部目标点；避障过程中，在每个时刻t(t=0,1,2,…)AGV接受传感器感知的环境信息、自身的位置姿态、运行速度等状态信息以及目标点的位置信息，AGV根据以上信息生成运动控制指令并执行，改变自身状态；每一步决策完成后时间推进ΔT，进入下一时刻t=t+1；当AGV无碰撞的到达局部目标点时完成避障，如果在该过程中与障碍物发生碰撞则避障失败。要解决的问题是得到局部避障策略πθ，在每个时刻t以观测到的信息为输入，输出运行控制指令。

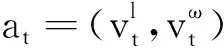
局部避障需要满足以下要求：①AGV在运行过程中不与障碍物发生碰撞；②局部规划以全局路径作为引导，避免过度偏离全局路径，避障结束后的运行方向与全局方向一致；③避障过程消耗的时间尽可能少；④确保避障路径的平滑性与AGV运行稳定性，控制指令不能大幅度变化。

无碰撞的要求表示为：在避障过程的每一个时刻t，AGV对任何障碍物都有R∩Bi=∅(i=1,2,…)，R表示AGV的几何形状，Bi为障碍物的几何形状。

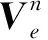
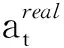
et=at-vt；

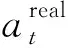
(1)

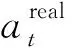
AGV在下一时刻的位置和姿态为:

(2)

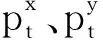
考虑到在实际运行中，局部目标点可能与障碍重合，因此判定AGV到达目标点不必严格要求AGV的位置与目标点位置重合或接近，只需整体运行轨迹与全局路径一致即可。结合上述全局路径引导的要求，AGV在Te时到达目标点可以表示为Vte·Ve>0、ΔVte·Ve>0，即AGV在全局方向上超过目标点、AGV的运行方向与全局方向一致。对观测信息做进一步补充，加入全局路径方向信息，同时将环境信息lt、引导向量Ve、位置向量Vt由全局坐标变换到以AGV位置为原点，以姿态方向为x轴的相对坐标系下，新的观测信息表示为ot=(lt,vt,Ve,Vt)。以最短时间完成避障表示最小化Te-Ts。

综上所述，智能工厂环境下的AGV避障问题可以转化为不确定环境下的从开始避障到结束避障的序列决策问题，优化目标为：

min(Te-Ts)。

(3)

决策变量为：

at=πθ(ot)。

(4)

约束包括：

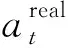
Vte·Ve>0；ΔVte·Ve>0。

(5)

2 部分观测马尔可夫决策过程构建

为了求解最优策略πθ，本文将局部避障问题构建为马尔可夫决策过程，由于观测数据ot只来自于对应的AGV，是对环境信息的部分观测，该决策问题属于部分观测马尔可夫决策过程(Partial Observational Markov Decision Process, POMDP)[15]。POMDP包含6个元素(S,A,P,R,Ω,O)，其中：S为环境的状态空间，包含AGV运行环境中的所有可能状态；A为动作空间，包括对AGV的控制指令；P为状态转移函数，表示执行动作后状态转移的概率；R为奖励函数，用来评价状态转移过程；Ω为观测空间(ot∈Ω);O为对环境状态的观测函数(ot=O(st))。在建立的模型中，AGV依据对环境的观测决策出控制指令，因此不需要考虑环境的相关元素，下面详细介绍避障问题中的观测空间、动作空间与奖励函数。

2.1 观测空间

AGV在时刻t观测到的信息ot包括周围环境数据lt、AGV运行速度vt、避障过程的全局路径引导方向Ve以及表示AGV位置与局部目标点位置的Vt，如图2所示。lt由布置在AGV前端的激光雷达扫描产生，可以探测180°的平面区域，角分辨率为1°，全部的雷达探测数据维度过高，不利于计算[16]，因此在每个时刻等间隔(15°)抽取13个数据(lt∈13)作为最终的输入，雷达测距半径为2.5 m；vt为AGV的运行速度，由AGV行驶的线速度和角速度表示(vt∈2)；Ve为表示全局路径方向的二维向量(Ve∈2)；Vt表示AGV与避障目标点的位置关系，同样由二维向量表示(Vt∈2)。

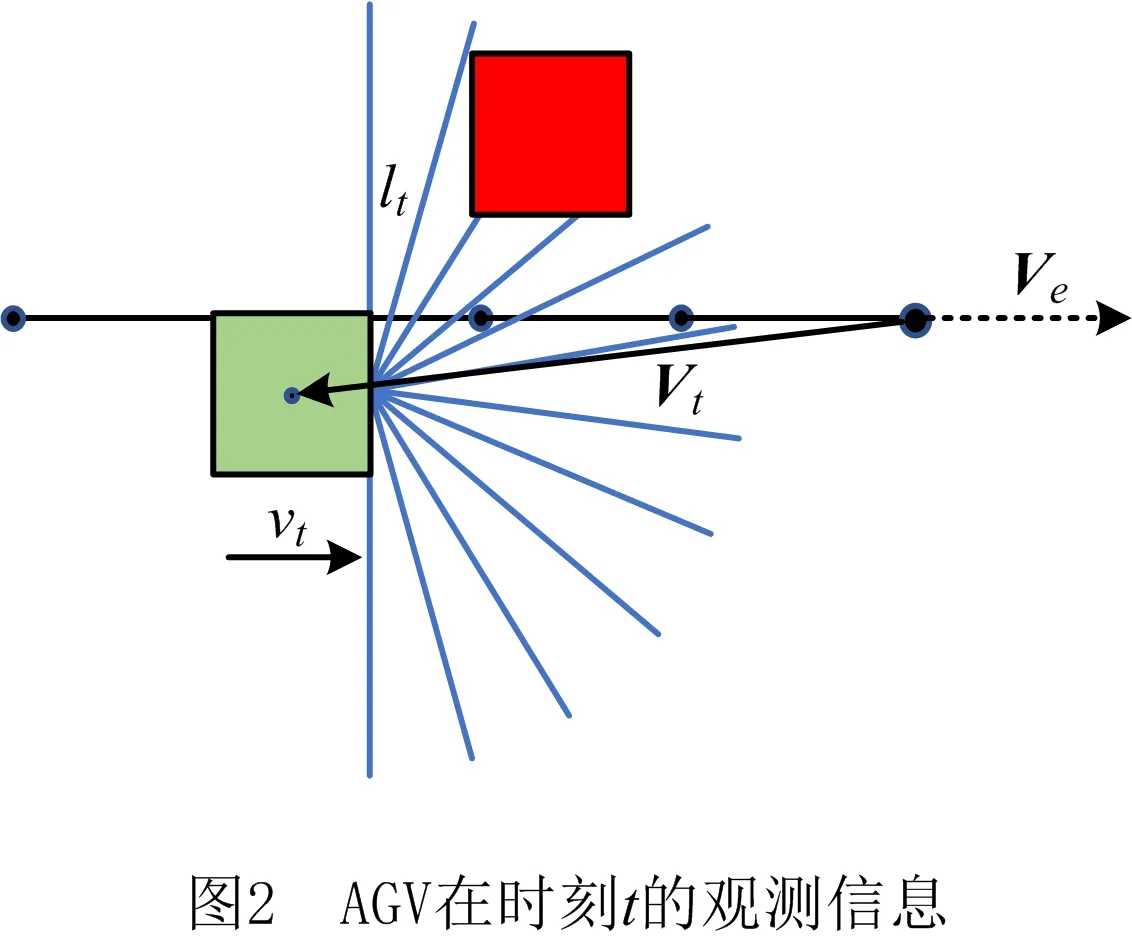
单次观测ot包含环境中障碍物的静态信息(如形状、位置等)，为了提高决策的有效性，需要利用环境中的动态信息，因此使用最近的N个连续观测值组成的观测序列ot=(ot+(-N+1),ot+(-N+2),…,ot)推测障碍的速度、运动趋势等信息。观测序列中的观测数量越多，包含的环境信息也越充分，可以提高决策的准确率，但过多的信息会影响计算的速度，对决策的时效性产生负面影响，综合考虑本文取N=3，即ot=(ot-2,ot-1,ot)作为观测序列。在开始避障的时刻t=0，观测序列取o0=(o0,o0,o0)。

2.2 动作空间

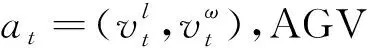
2.3 奖励函数

局部避障路径规划的目标是在无碰撞约束、全局路径引导约束、轨迹平滑约束下以最短的时间完成避障。上文通过对动作进行PID控制处理实现了轨迹平滑约束，下面介绍奖励函数的设置以实现优化目标与其余两种约束。

本研究的奖励函数设置为：

(6)

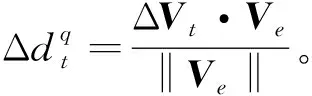
(7)

切向奖励根据切向距离的大小与固定奖励成比例。

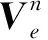
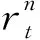
(8)

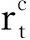
3 基于深度强化学习的避障策略求解

局部避障问题最终需要求解得到最优避障策略πθ(at|ot)，在建立的模型中观测状态ot属于高维连续输入，输出的动作at同样也是连续的，因此本文采用深度强化学习算法中的DDPG算法[17]训练确定性策略，在每一步决策出最优的动作。

3.1 网络结构

DDPG算法中包含动作(Actor)和评价(Critic)两种神经网络，分别对策略与价值近似表征。Actor网络以观测序列o为输入，输出动作a，控制AGV的行驶速度和方向，为AGV规划出避障路径，表征避障策略πθ(at|ot)[18]；Critic网络以观测序列o和动作a为输入，输出二者的价值Q(o,a)，对Actor网络的决策结果进行评价，使其能够不断优化。

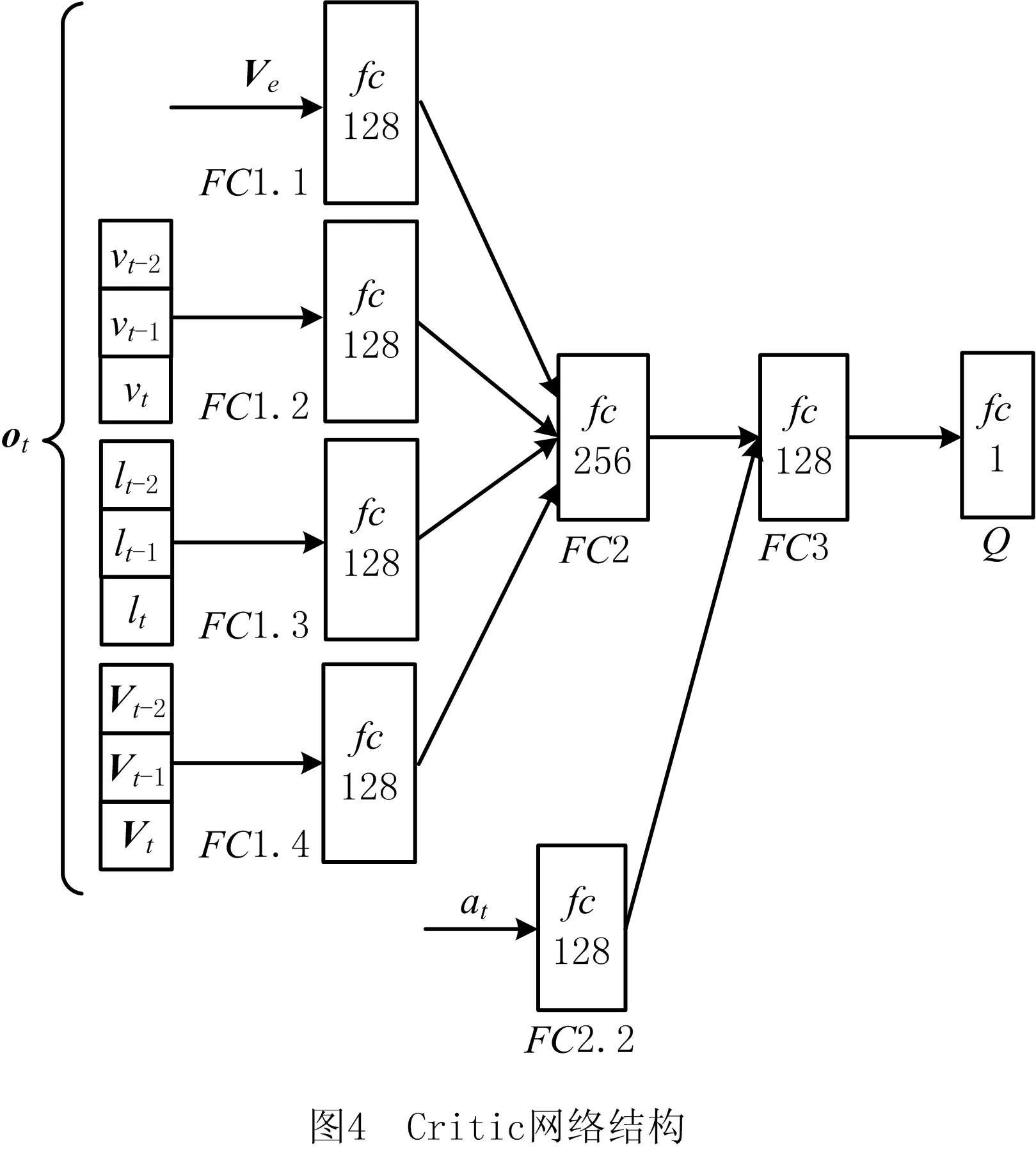
本文选取决策时刻观测数据和前两个时刻的观测数据组成观测序列，以多帧序列数据作为决策所需的输入数据。为了解决多帧序列输入的决策问题，本文针对Actor和Critic网络设计了如图3和图4所示的架构。

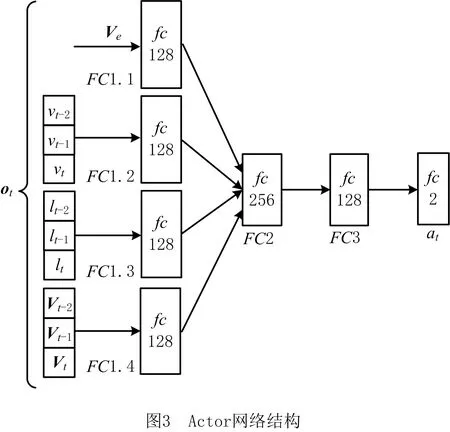
如图3所示为Actor网络，观测序列o被分为全局路径方向Ve、AGV速度序列(vt-2,vt-1,vt)、雷达探测序列(lt-2,lt-1,lt)和AGV位置序列(Vt-2,Vt-1,Vt)，单帧数据Ve连接全连接网络，3种多帧序列输入数据按照先后顺序堆叠为一维向量分别连接全连接网络，中间层及最后的输出层均为全连接网络，Actor网络的具体参数如表1所示。

表1 Actor网络参数

如图4所示为Critic网络，与Actor网络类似，Critic网络同样采用数据堆叠的方法处理多帧序列输入问题，因为Critic网络是对观测—动作(o,a)进行评价，所以还添加了动作处理层，Critic网络的具体参数如表2所示。两种网络中用到的激活函数包括：双曲正切函数tanh(x)和relu(x)=max(0,x)。

表2 Critic网络参数

3.2 算法流程

DDPG算法是基于Actor-Critic(动作—评价)网络的确定性策略梯度算法，算法使用经验回放与备份网络的方法提高数据利用率与算法稳定性。本文利用DDPG算法训练避障策略的流程如下：

(1)随机初始化Critic网络Q(o,a|θQ)和Actor网络μ(o|θμ)，初始化参数γ(奖励折扣因子)、τ(网络更新率)、l(学习率)；(2)复制Critic和Actor的网络参数，初始化目标网络Q′(o,a|θQ′)和μ′(o|θμ′)，θQ′←θQ，θμ′←θμ；(3)初始化经验存储池，容量为P，设置经验采样数M(M≤P)，设置训练回合数E；(4)训练E次：

1)初始化策略探索噪声aN;

2)AGV检测到障碍物，进入避障状态，时间步t=0，获取雷达扫描数据、AGV运行速度、全局路径方向以及AGV位置向量，构建初始观测ot=o0；

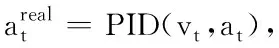
5)向经验池中存入状态转移过程(ot,at,rt+1，ot+1,isDone)；

6)从经验池中随机抽取M个状态转移过程；

7)使用两种目标网络Q′(o,a|θQ′)和μ′(o|θμ′)计算观测—动作的目标价值yi，

yi=ri+1+γQ′(oi+1,μ′(oi+1|θμ′)|θQ′)

8)采用梯度下降方法以学习率l更新Critic网络，目标是最小化对价值的评价误差，使Critic对价值的估计更准确，损失函数为：

9)采用梯度上升方法以学习率l更新Actor网络，目标是最大化价值，使Actor选择更好的动作，损失函数为：

10)更新目标网络

θQ′←τθQ+(1-τ)θQ′

θμ′←τθμ+(1-τ)θμ′

11)时间步更新t=t+1；

12)重复步骤3)～步骤11)，直到避障结束，此回合结束。

(5)训练结束。

在上述算法的每一回合中，Actor网络表示避障策略，输入观测o，输出控制指令at，在对at处理后由仿真环境中的AGV执行，AGV根据at改变自身位置和速度，仿真环境根据式(6)计算相应的奖励rt+1，并产生新的观测ot+1，同时判断是否完成了避障(isDone)。每一步可以表示为一个状态转移过程(ot,at,rt+1,ot+1,isDone)，并将其存入经验池中。当经验池中积累了足够多的状态转移过程后即可用来更新网络参数，优化网络。

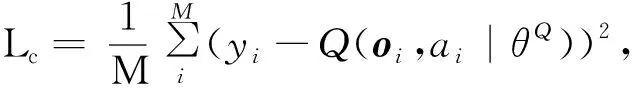
算法中的相关参数如表3所示：

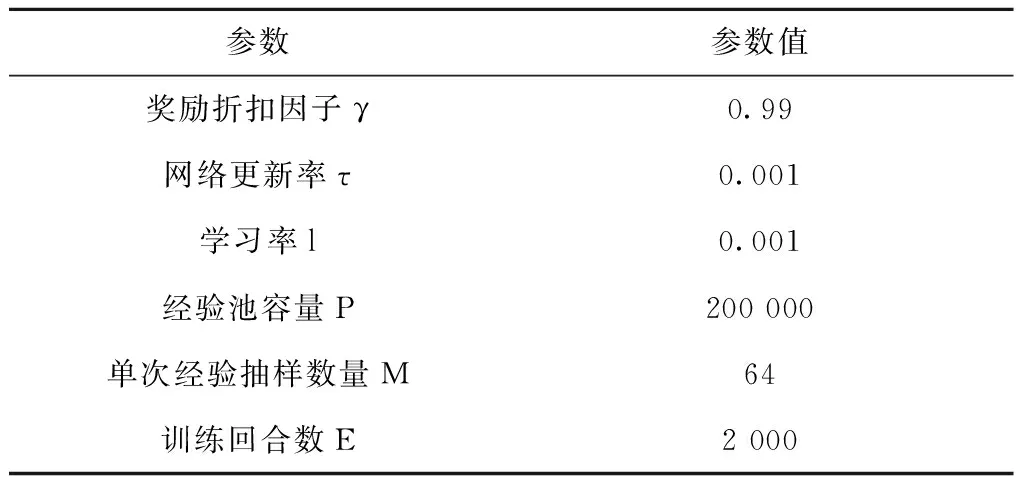
表3 算法参数设置

3.3 避障策略训练

本文使用编程语言Python 3.8搭建仿真环境，实现了AGV状态更新、雷达感知、AGV碰撞检测等功能，模拟AGV运行，使用Pytorch 1.9开发包编写DDPG算法，硬件采用AMD Ryzen7-4800处理器和RTX 2060显卡。

在训练避障策略时，每个回合随机设置静态障碍、AGV的引导路径及AGV的初始避障状态(包括位置、姿态、线速度、角速度)，设置多台AGV同时运行，每台AGV与环境交互生成经验并利用DDPG算法训练避障策略，同时也作为其他AGV运行时的动态障碍。策略训练仿真环境的相关参数如表4所示。

表4 避障策略训练环境参数设置

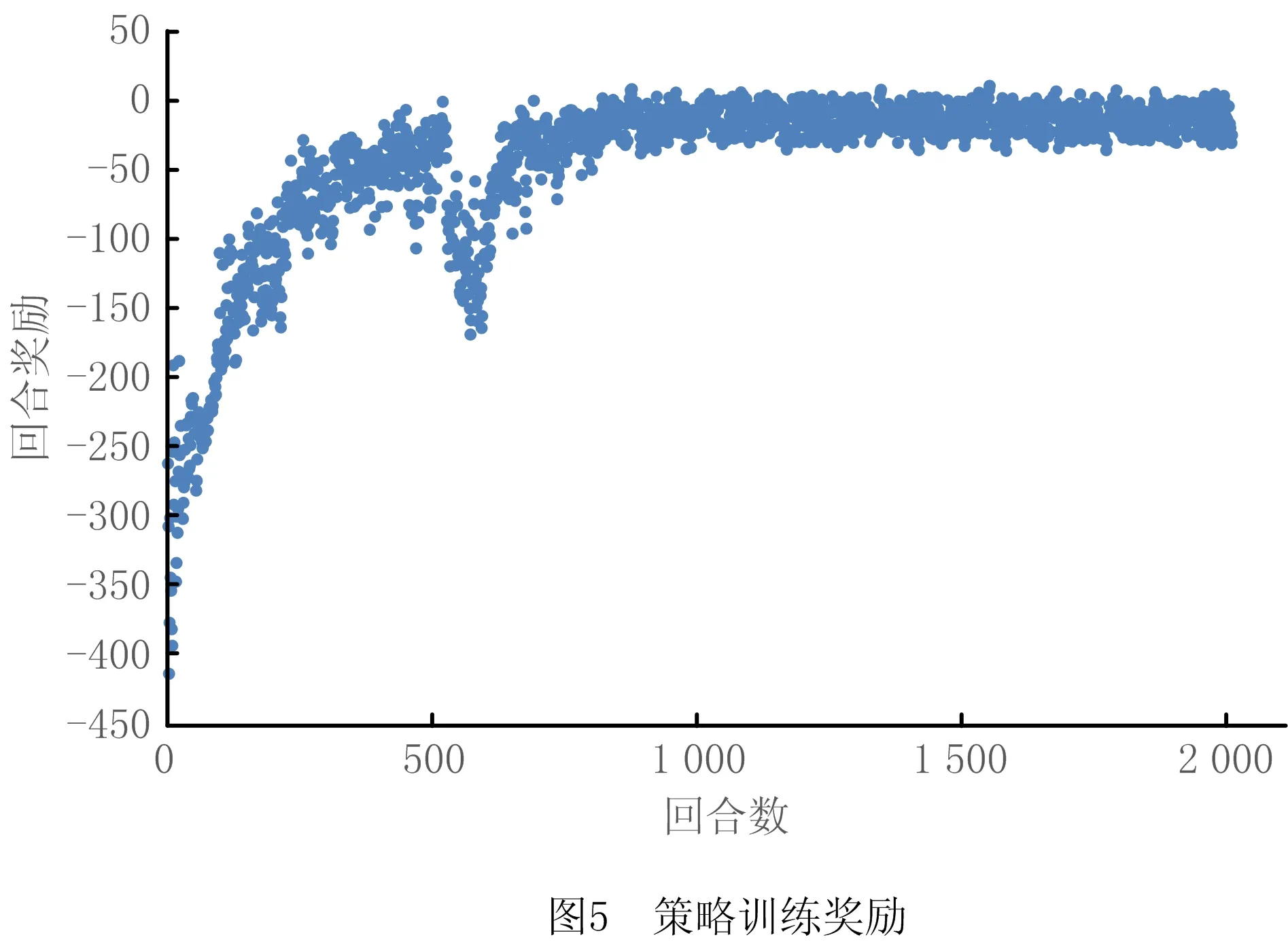
基于构建的仿真环境和3.2节的算法流程训练避障策略，训练过程中每个回合得到的奖励值如图5所示。由图5可以看到，训练后期可以获得较大奖励且奖励值保持平稳趋势，表明算法已经收敛。策略训练时每回合的障碍分布和多AGV状态随机设置，因此奖励值会出现微小波动。

4 仿真实验与分析

本文提出的方法在避障时考虑了后续路径方向的引导作用，因此对避障策略的避障性能与整体运行效率进行实验分析，并与现有的只以目标点作为引导，不考虑后续方向的策略[15]进行对比。基于3.3节介绍的仿真环境开展单次避障与长距离多次避障实验。

4.1 评价指标

本文采用以下3种指标对避障性能和效率进行评价：

(1)成功率αAGV成功完成避障次数占总避障次数的比率；(2)额外时间比teAGV完成避障消耗的时间除以预期时间，预期时间指AGV在无障碍环境下以最大速度到达目标点所需时间;

(3)额外距离比deAGV避障过程的行驶距离除以预期距离，预期距离指避障起始点到目标点的路径距离。

4.2 单次避障测试

在实际应用中，当AGV之间的路径重合或者交叉时即有碰撞风险[20]，本文设计了交替、交叉以及十字形3种实验场景，场景中包含4台AGV，如图6所示。

(1)交替场景 AGV路径重合，两端的AGV运行方向相反；(2)交叉场景 AGV路径垂直交叉，且交叉位置在路径中间部分；(3)十字形场景 同时包含路径交叉与重合。

在不同场景下进行1 000次避障实验，每次实验时为AGV在路径方向的位置增加随机扰动，使AGV的开始避障位置发生变化。分别采用本文得到的避障策略和文献[15]无方向引导的避障策略控制AGV完成避障实验，实验结果如表5所示，两种策略下的AGV避障轨迹如图6所示，图中不同AGV使用不同颜色标出，从开始避障到结束，AGV轨迹的颜色由浅变深。

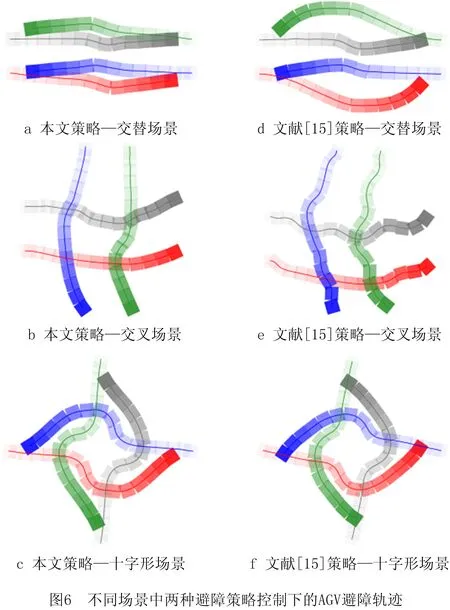
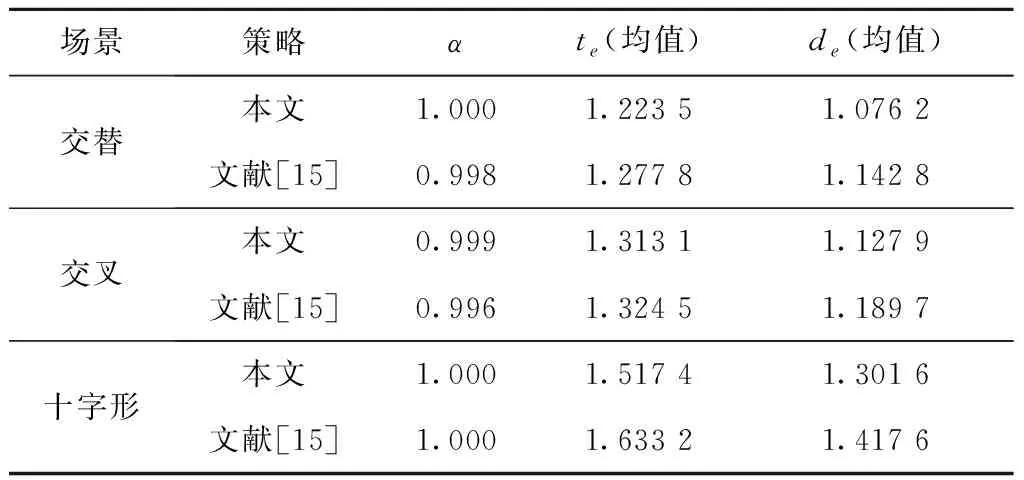
表5 不同场景下的避障结果

4.3 长距离多次避障测试

为了探究避障策略对AGV整体运行效率的影响，本文设计了长距离运行实验，在实验中AGV需要多次躲避障碍完成较长距离的运行。实验场景如图7所示，实验场景为40 m×3 m的矩形，场景中间设置0.6 m×0.6 m的矩形块障碍，AGV需要从左端运行到右端。设置不同密度障碍的实验场景，障碍的间距分别为5 m、4 m、3 m，对应的障碍数量为7个、8个、11个。

在每种场景下进行1 000次实验，每次实验时随机设置障碍物在竖直方向的位置，分别以本文策略和文献[15]的策略控制AGV运行，实验结果如表6所示，AGV运行轨迹如图7所示。

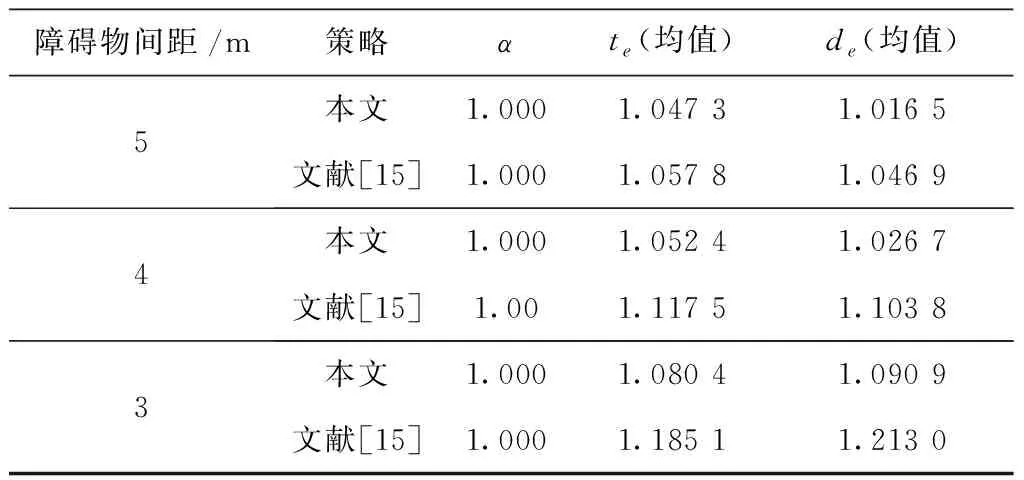
表6 不同障碍密度场景下的运行结果

4.4 实验结果分析

经过上述实验测试，本文提出的局部避障方法可以为AGV规划出有效的避障轨迹，保证AGV的无碰撞运行，避障成功率α已达或接近100%。在单次避障实验中，相比于不考虑后续方向引导的方法，本文方法使AGV在避障时偏离路径的程度更小，可以缩短5%左右的行驶距离。

在长距离多次避障测试中，本文方法可以使AGV避障结束后的运行方向与后续路径方向尽可能保持一致，在障碍物密集环境下可以有效提升运行效率，在实验中，当障碍物间隔为3 m时，行驶时间和距离分别缩短8.8%和10.1%。

由于是以避障时间最短为优化目标，AGV在避障时与障碍物的间距较小，运行轨迹对障碍的位置和形状敏感，在现实中可能会因为误差等原因导致安全问题，因此后续还需针对数据误差等问题做进一步研究，提升方法的鲁棒性。

5 结束语

本文针对智能工厂复杂动态环境下的AGV无冲突运行问题，提出一种基于深度强化学习的局部避障路径规划方法。主要研究内容包括：将局部避障路径规划问题表征为部分观测马尔可夫决策过程，考虑了后续路径方向对避障的引导作用，介绍了观测空间、动作空间和奖励函数；设计DDPG算法求解最优避障策略，利用多帧数据评估障碍物的运动趋势，使AGV可以应对动态环境；最后设计仿真实验对训练出的避障策略进行验证，实验结果表明本文所提方法可以为AGV规划出安全的行驶轨迹，相比于现有方法可以提升运行效率。

本研究提出的方法是以传感器观测到的外部环境数据作为输入，没有充分考虑AGV自身的参数，如尺寸、载重等，下一步的研究将尽可能全面地考虑影响避障的因素，提高AGV的避障能力。