自适应多种群Jaya算法求解绿色并行机调度问题

王建华，杨 琦，朱 凯

(江苏大学 管理学院，江苏 镇江 212013)

0 引言

在并行机调度问题中，设置操作长期以来被认为是可以忽略或被认为是处理时间的一部分，虽然这对于一些调度来说是合理的，但对于有些情况下是需要明确的[1]。例如，化工厂在加工一种混合物转换到另一种混合物时，反应器必须经过清洗，清洗时间取决于之前的工作和后续的工作。如果前一种化学物质影响后一种化学物质，可能需要很长的清洗时间，以相反顺序只需更短时间[2]。另一方面，当今社会环境问题日益严重，绿色制造研究备受关注。作为现代制造模式，绿色制造旨在保证产品功能与质量的同时减少能源浪费，实现经济指标和绿色指标的协同优化[3-4]。因此，形成了本文所研究的具有设置时间的绿色并行机调度问题(Green Parallel Machine Scheduling Problem with Set-up Time, GPMSP-ST)。

目前，解决并行机调度问题常用到精确算法、近似算法以及智能优化算法。精确算法包括分支界定，最速下降法等运筹学算法[5-6]，该类算法在小规模问题中能在短时间内获得最佳解，但面对较大规模问题时，求解时间较长，若问题具有非凸性，则不存在通用的最优解求解算法。基于动态规划的近似算法可以提出能够保证最优解不丢失的递推方程，在较长时间内能够保证算法获得最优解，但其本质上仍属于穷举法，时间复杂度基本为指数型，且只能应用于能提出相应规则的简单并行机调度问题[7-9]。相较于前两种算法，智能优化算法具有求解速度快、普适性强、求解质量高等优点，近年来得到了广泛研究。轩华等[10]基于遗传算法和禁忌搜索算法提出一种混合启发式算法求解了每阶段含不相关并行机的多阶段混合流水车间问题。宋强[11]以异构并行机为研究对象，提出混合多目标教与学算法解决了最小化makespan和提前、延误惩罚总成本的多目标问题。时维国等[12]以最小化最大完工时间为单目标，提出一种改进灰狼算法，有效解决了带相同并行机的混合流水车间调度问题。付亚平等[13]针对生产中存在的串并联共存的布局环境，研究了特殊的混合并行机调度问题，并提出一种改进的非支配遗传算法进行求解。张洁等[14]构建了一种两阶段蚁群并行搜索算法，对于非等效并行机车间调度问题，明显提高了获得较优解的概率。以上文献并未涉及工序间的设置时间，当加工不同工件由于设置操作产生序列相关准备时间时，设置时间就必须明确。胡大勇等[15]以最小化最大完工时间为目标，研究了设置时间与顺序相关的等同并行机调度，对建立的数学规划模型所求问题下界评价了遗传算法所得近似最优解的质量。何雨洁等[16]验证了所提出的混合离散教与学算法可以有效解决广泛存在的复杂并行机调度问题，即带到达时间、加工约束、多工序和工序间设置时间的并行机调度问题。李作成等[17]针对带工件加工约束和序相关设置时间的异构并行机调度问题，提出一种分布估算方法并验证了其有效性和鲁棒性。FANJUL-PEYRO等[18]提出了新的混合整数线性规划和基于数学规划的算法，经过测试比较现有模型和算法，证实了该算法在具有作业序列设置时间的不相关并行机调度问题上的求解效果更好。VALLADA等[19]针对带工序设置时间的异构并行机问题，提出一种性能优异的增强局部搜索的遗传算法。YEPES-BORRERO等[20]考虑了异构并行机中具有设置时间和设置中附带额外资源的情况，设计了3种元启发式算法，并证实了考虑资源约束的算法能产生更好结果。在关于并行机调度的研究中，基本以最小化完工时间这类经济指标为优化目标，近年来，逐渐有学者考虑能耗等绿色因素。李凯等[21]考虑了具有能耗成本约束的并行机调度问题，提出了改进的最早交货期优先(Earliest Due Date firstly, EDD)算法并验证了其有效性。

根据已有文献来看，在考虑设置时间的并行机调度问题上，考虑能耗、碳排放等绿色指标的文献尚不多见，且大多研究采用传统智能优化算法。VENKATA RAO教授[22]在2016年提出的Jaya算法相较于其他智能优化算法具有无参数控制、求解速度快、全局搜索能力强等优点。近年来，Jaya算法也逐步应用到车间调度领域，但大部分研究集中在流水车间调度问题领域，少有应用于并行机调度领域内。因此，本文建立了最小化最大完工时间与最小化机器总能耗的双目标优化模型，在Jaya算法的基础上，设计子种群数量可随搜索情况自适应改变的多种群策略，形成可以求解多目标的自适应多种群Jaya算法(Self-Adaptive Multi-Population Jaya algorithm, SAMP-Jaya)，经过测试分析，验证了该算法求解GPMSP-ST问题的有效性与鲁棒性。

1 具有设置时间的绿色并行机调度问题

1.1 问题描述

考虑序列相关准备时间的异速并行机调度问题由m台并行机器和n个工件组成，每个工件可以在任意机器上加工且每个工件只需加工一次。工件加工时间取决于机器的性能，在不同的机器上加工时间往往不同。同一机器上加工不同工件时，需要一定加工准备时间，不同工件间加工准备时间基本不同，处于加工准备时间时，机器为空载状态，能耗为空载能耗。绿色并行机调度问题在优化最大完工时间的同时，也需考虑机器能耗，保证经济指标与绿色指标的优化同步进行。

1.2 问题模型

为了构建当前调度的数学模型，现定义相关符号如表1所示。

表1 符号定义

根据上述定义，建立如下数学模型，优化目标为最小化最大完工时间和最小化机器总能耗。

(2)

s.t.

(3)

k=1,2,…,m;h=1,2,…,qk。

(4)

k=1,2,…,m;h=1,2,…,qk。

(5)

k=1,2,…,m;h=1,2,…,qk。

(6)

(7)

(8)

Xikh={0,1};i=1,2,…,n;k=1,2,…,m;h=1,2,…,qk。

(9)

其中：式(1)和式(2)为数学模型中的双目标函数；约束(3)表示每个作业都能调度到一台机器上；约束(4)确保每台机器同一加工位置只能加工一个工件；约束(5)保证工件一旦开始加工，则不能中断；约束(6)表示同一机器上相邻加工位置存在前后紧前关系；约束(7)表示每台机器加工时间起始时间为0时刻；约束(8)表示每台机器的第一个加工工件不需要设置时间；约束(9)表示Xikh只能为0或1。

2 自适应多种群Jaya算法

GPMSP-ST为离散型问题，对于求解连续性问题的Jaya算法而言，本文设计了一种排序机制将离散与连续结合起来。此外，为了提升初始种群的质量，随机选择两种机器分配规则中的一种。相较于固定种群，多种群方法可以将整个种群分为多个子种群并将其分配至整个搜索空间，每个子种群具有在不同区域搜索的能力，从而可以提高搜索多样性，有效检验问题的变化。GPMSP-ST为多目标问题，解的优劣性需要衡量多个目标值，本文采用非支配排序的方法给解划分等级，通过计算各等级拥挤度得到最优解与最劣解。SAMP-Jaya算法不需要调整特定于算法的参数，求解效果具有良好的鲁棒性。多种群的搜索有助于提升算法全局搜索能力，不易陷入局部最优。

2.1 编码与解码

GPMSP-ST可以分为工件排序与机器分配两个子问题。本文采用二维实数编码方式，可以有效映射问题的解空间。设每一个解矩阵X包含两个向量，分别为基于工件排序的向量X1和基于机器分配X2，现有一个9×3 GPMSP-ST的例子，X1=[1,5,4,9,8,2,6,3,7]，X2=[2,3,2,1,3,2,2,1,3]，表示工件1在2号机器加工，工件5在3号机器加工，以此类推。3台机器的加工工件顺序矩阵分别为Y1=[9,3]，Y2=[1,4,2,6]，Y3=[5,8,7]。编码示例如图1所示。

工件在各机器加工时间和工件间设置时间如表2和表3所示。

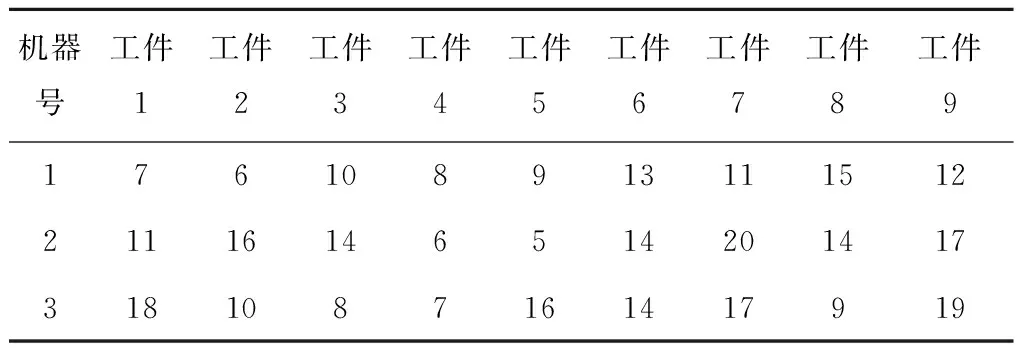
表2 工件加工时间

表3 各工件间设置时间

此例中，经解码后，其调度甘特图如图2所示。

2.2 多规则种群初始化

高质量种群有助于算法的寻优，但是为避免算法陷入局部最优，同时也要考虑种群多样性，因此本文采用多规则初始化种群，依然以2.1节中9×3的问题为例。

工件加工向量初始化：首先为加工工件序列创建数值为0～1随机值的位置向量Z1=[A1,A2,A3,…,A9]，然后将所有数值按降序进行排序，最后将位置向量数值所对应的原工件序列更换位置，具体步骤如图3所示。

机器分配向量初始化：每个种群个体初始化时会随机产生一个0～1的随机数，然后根据CALDEIRA等[23]提出的规则结合本文问题形成如下规则进行机器分配：

(1)随机规则 若随机数小于0.8，为每个工件随机分配相应的机器。

(2)工作量均衡规则 若随机数大于等于0.8，根据工件加工顺序逐一为每个工件分配机器，每当为一个新工件分配机器时，将统计所有机器被使用次数，优先分配尚未达到使用平均数的机器给待分配机器的加工工件，倘若有若干机器可供选择，随机选择一台机器。

2.3 种群的划分与合并

多种群相比于固定数量的种群，子种群的数目与选择将是算法性能的关键问题。为了满足种群的多样性，SAMP-Jaya算法将对VENKATA RAO等[24]提出的多目标Jaya算法(Multi-Objective Jaya algorithm, MO-Jaya)作出如下修改：

(1)根据解的质量划分多个子种群，使用子种群的数量将解分布在搜索空间上，而不是集中在某个特定的区域内，因此，算法有望产生最优解。

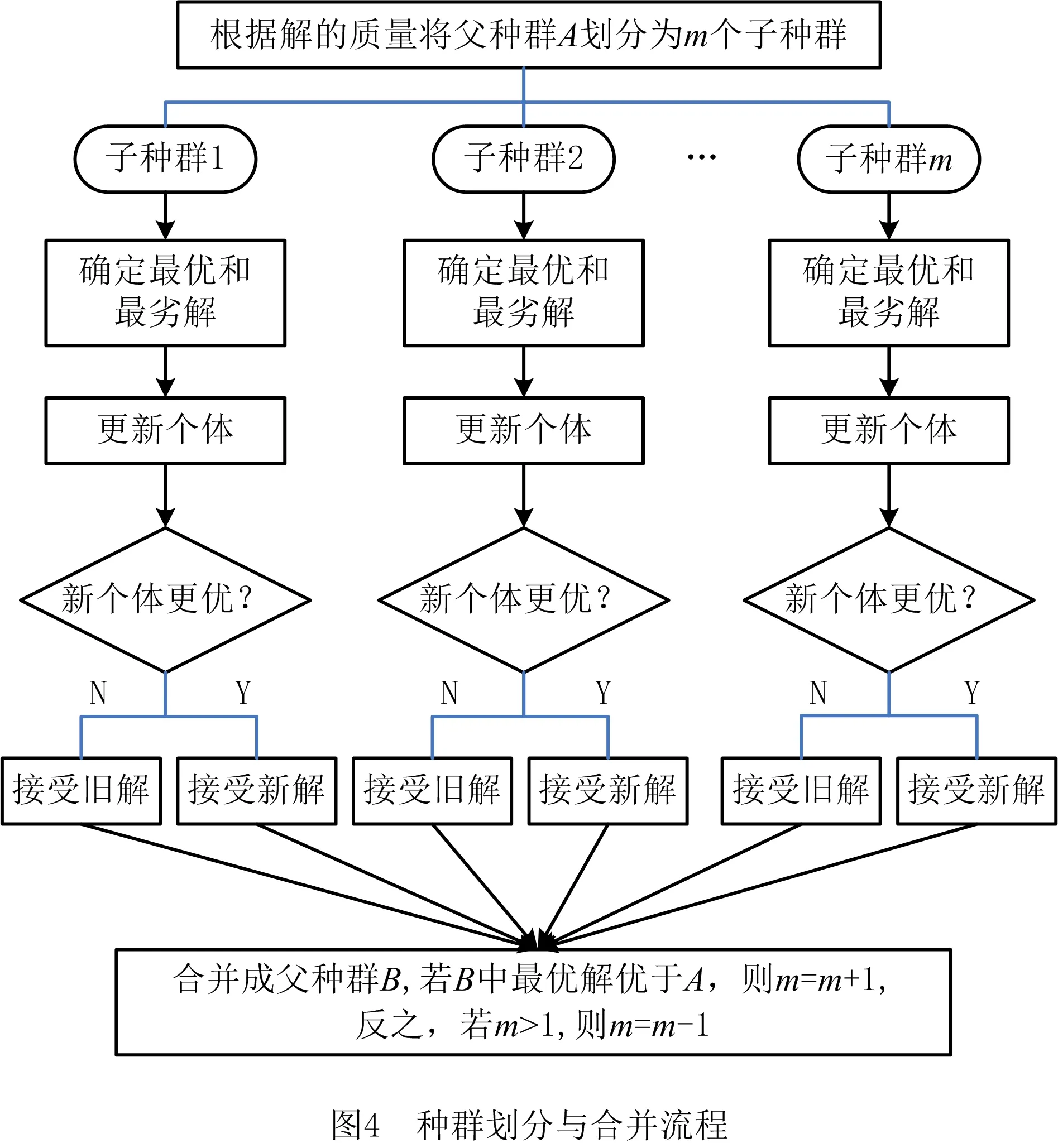
(2)根据解的变化情况自适应改变子种群数量，以跟踪最佳解决方案并改进搜索过程多样化，此外，重复解被新生解所代替，以保持算法多样性和勘探性。若第n代种群被划分为m个子种群，经过更新后形成新子种群并且合并成第n+1代新种群。当新种群的最优解优于旧种群时，则m=m+1，目的是为了增加搜索过程的探索特性，否则m=m-1，因为算法更需要开发性而不是探索性。

种群的划分与合并过程如图4所示。

2.4 Pareto寻优及个体拥挤度计算

在单目标优化的情况下，很容易根据解的适应度来判断解的优劣性。但是在存在多个冲突目标的情况下，很难从一组解中决定最优解与最劣解。为了有效处理多个目标，本文利用非支配等级以及个体拥挤度两种指标来评价个体解。基于优势概念可以将群体划分几个等级。其规则如下：设有两个解方案Xi和Xj，只有当Xi在所有目标方面不比Xj差，并且至少在一个目标上严格优于Xj时，解Xi支配解Xj，即解Xi具有更高的等级。等级高的解被认为优于其他的解。若两个解拥有相同的等级，具有较高拥挤距离的解被视为优于其他解[25]。这保证了从搜索空间的稀疏区域中选择解决方案，有助于提升解的多样性。拥挤度(Crowding Distance, CD)计算步骤如下：

步骤1对于每一个目标函数，将等级相同的解按相应目标函数值递增顺序排序。

步骤2设排序集合中有n个解，将边界解(第一个解和第n个解)分配最大拥挤距离CD=∞，对于排序集合j=2到n-1中所有其他解，拥挤距离为：

(10)

具有最高等级且拥挤度最高的为最优解，反之为最劣解。当二者确定后，新种群中每个个体将根据2.5节中更新公式进行更新。

2.5 种群个体变量更新策略

Jaya算法在每一轮迭代时会更新每个变量值，变量的值更新后，其新目标值将与旧值比较，只有更好的解才被考虑用于下一代。其更新公式如下所示：

H(i+1,k)=H(i,k)+r1(H(i,b)-

|H(i,k)|)-r2(H(i,w)-|H(i,k)|)。

(11)

式中：i，k分别表示迭代和候选解的索引；H(i,k)表示第k个候选解在第i次迭代后的变量值；r1和r2是[0,1]范围内产生的随机数，二者充当比例因子，确保解良好的多样化。与此同时，每次更新，候选解都尝试接近最佳解并远离最差解，因此，实现了搜索过程良好强化与多样化的同步性。

SAMP-Jaya算法继承了Jaya算法的更新思想，即试图接近成功(达到最佳解)，并试图避免失败(远离最差解)。并在此基础上设计了一种位置向量更新机制来解决离散型变量更新问题。工件加工顺序码更新过程如图5所示。

机器分配经过初始化规则后，其更新过程与图5类似。

2.6 SAMP-Jaya算法流程

SAMP-Jaya算法具体步骤如下：

步骤1根据2.1节描述设计变量，2.2节中的规则初始化种群，并设置迭代次数为终止条件。

步骤2计算种群中每个候选解的所有目标值。

步骤3基于解的质量，将整个种群划分为m个组(m的初始值为2)。

步骤4每个子种群使用2.5节描述的更新规则独立更新每个种群的解，每一个修改后的解只有比旧方案更好的情况下才被接受(修改后的解被支配)。

步骤5将所有子种群合并为一个整体，并根据2.3节描述修改m值。

步骤6检查终止条件。若搜索过程已经达到终止条件，则终止循环并输出最佳解决方案，否则返回步骤2。

3 算例测试与分析

3.1 测试准备

在频率为2.10GHz，内存4GB，AMDA8-5550MAPU的计算机上进行仿真，选用NetBeansIDE8.2进行编程，为体现实验结果的公平性，各算法相同参数设置为：种群大小为50，终止条件为迭代次数为200代。

3.2 SAMP-Jaya与两种智能算法比较分析

为了验证本文所提出的SAMP-Jaya算法的优越性，将SAMP-Jaya算法与ABREU等[26]提出的混合遗传算法(HybridGeneticAlgorithm,HGA)、何雨洁等[16]提出的混合离散教与学算法(Hybridmulti-objectiveTeaching-Learning-basedOptimization,HDTLBO)进行比较。根据上述两篇文献已有测试结果表明，取两种算法较优表现参数如表4所示。

表4 两种算法参数取值

以最大完工时间为单目标，测试算例是随机生成的，其中处理和设置时间是从U(50,100)和U(125,175)中两个均匀分布中随机提取。共有如下3种情况：①当处理和设置时间平衡(ProcessingSetupBalanced,PSB)时，它们都是从U(50,100)中提取的；②当处理时间占据主导(ProcessingDominant,PD)时，处理时间和设置时间分别从U(125,175)和U(50,100)中提取；③当设置时间占据主导(SetupDominant,SD)时，处理时间和设置时间分别从U(50,100)和U(125,175)中提取。测试问题的规模n和m的集合分别为{20,40,60,80,100,120}和{2,4,6}。将SAMP-Jaya算法运行15次，比较各算法的最优解与标准偏差(StandardDeviation,STD)如表5所示。表中粗体表示相同算例中优于其他算法的最优解。

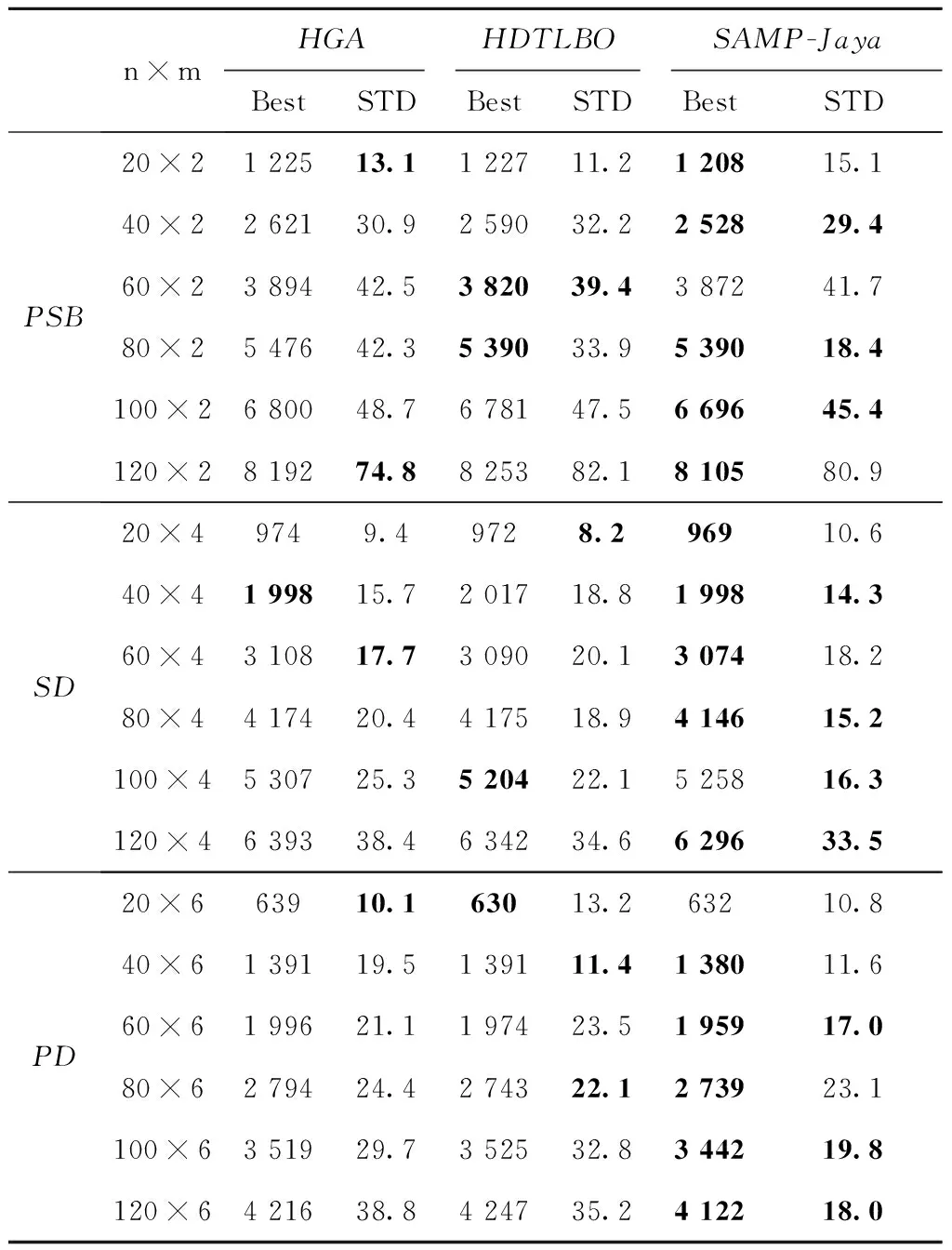
表5 各算法最优解与标准差对比

由表4中所有算例可以发现，相较于其他两种算法，SAMP-Jaya算法所得最优解次数总计为15次，只在3种规模的算例中未取得最优；在所有规模问题中均表现良好，在未取得最优解的3种算例中也接近其他算法的最优解，综合效果相较其他两种算法更加优越。所得标准差中，SAMP-Jaya算法所得结果在10次中获得较小值，HGA算法与HDTLBO算法分别在4种不同算例下取得最小值，所得结果表明SAMP-Jaya算法离散程度整体更加稳定，算法具有良好的鲁棒性。

以PD情况下40×6规模问题为例，如图6所示为其最大完工时间为1 380的最优调度甘特图,其中：括号内数字为工件号，其余数字均为加工或设置时间。

3.3 SAMP-Jaya求解GPMSP-ST性能分析

为了验证SAMP-Jaya求解GPMSP-ST问题的性能，本节以最大完工时间与能耗为双目标，在PSB情况下，采用20×8，40×8，60×8，80×8，100×8，120×8规模问题，单位加工能耗在(10 J,30 J)中均匀分布，单位空载能耗在(1 J,5 J)中均匀分布。比较SAMP-Jaya算法与MO-Jaya算法，以及MENG等[27]提出的变邻域结构遗传算法Ⅲ(Variable Neighborhood Structure Genetic Algorithm Ⅲ, VNSGAⅢ)在求解质量和收敛性能两个方面的效果。采用非支配解集数量(N)、非支配解集占参考解集比率(NR)、世代距离(GD)和反世代距离(IGD)4个指标来评价3种算法所求非支配解集质量的优劣，后3项指标定义如下：

(1)NR。该比率表示所衡量算法所获得的非支配解占参考解集的比率。较大的NR值表示算法可以获得更多最优解，其计算公式为：

(12)

(2)GD。表示所测算法中非支配解集各点与参考解集的平均距离，其计算公式为：

(13)

式中：di表示Dj中第i个解到到D*中最近点的欧式距离，n表示Dj中解的个数。GD越小，算法性能越好。考虑到两个目标量纲不同对指标产生的影响，对目标采用归一化处理如式(14)所示：

(14)

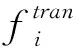
(3)IGD。为综合性测量指标，表示参考解集中各点到所测算法中非支配解集之间的平均距离，其计算公式为：

(15)

式中：xi表示D*中第i个解到到Dj中最近点的欧式距离，n*表示D*中解的个数。对所有目标值均采用归一化处理。

对于各测试算例，将3种算法均独立运行15次，所得各指标平均值如表6所示，3种算法所得最优指标加粗显示。

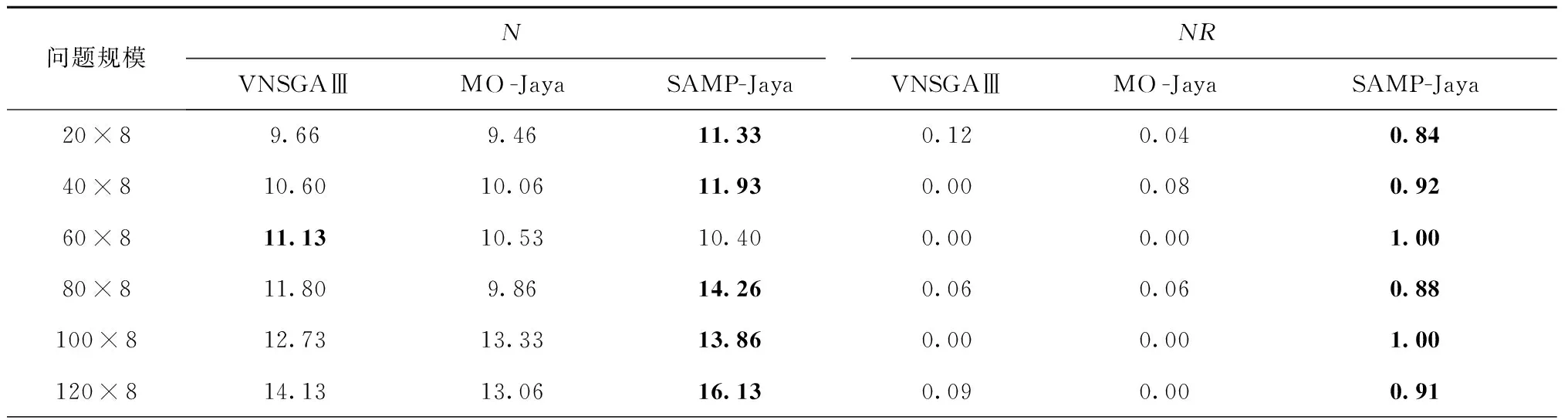
表6 3种算法4项指标对比

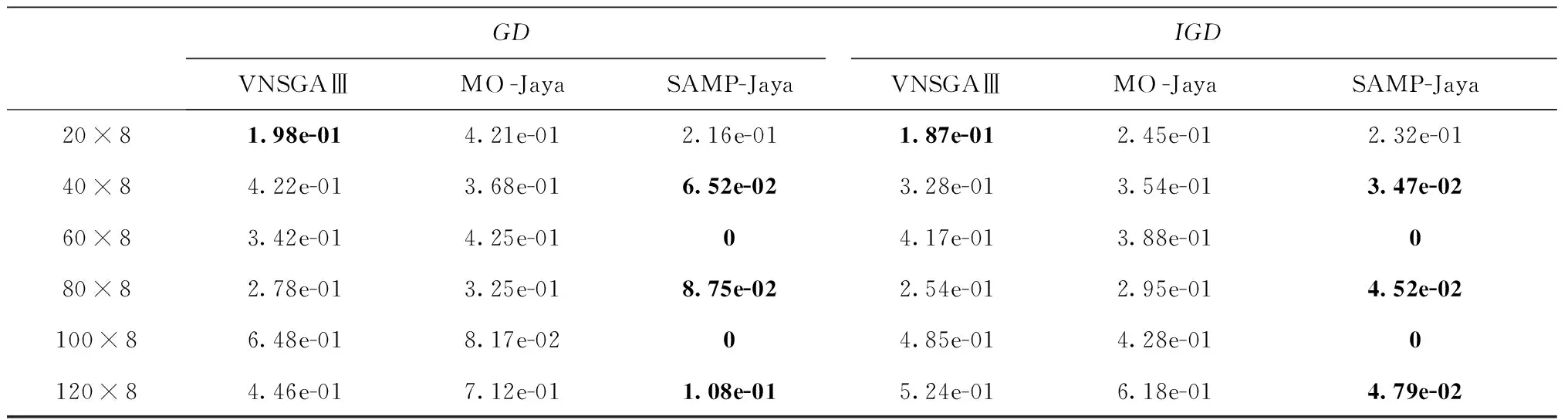
续表6

由表中测试结果可知，就N指标而言，SAMP-Jaya算法在5种算例中取得最优值，说明该算法全局搜索能力更强，意味着更多种方案可供选择；在NR、GD、IGD三种指标中，SAMP-Jaya算法均表现良好。就NR指标而言，SAMP-Jaya算法所有测试结果均等于或接近1，说明该算法在各算例中所得非支配解大多数优于其他算法的非劣解；以GD、IGD指标而言，SAMP-Jaya算法在5种算例测试结果中均为最小值，说明该算法所得非支配解集更加接近问题真实Pareto前沿，相较于其他两种算法收敛性能更佳。

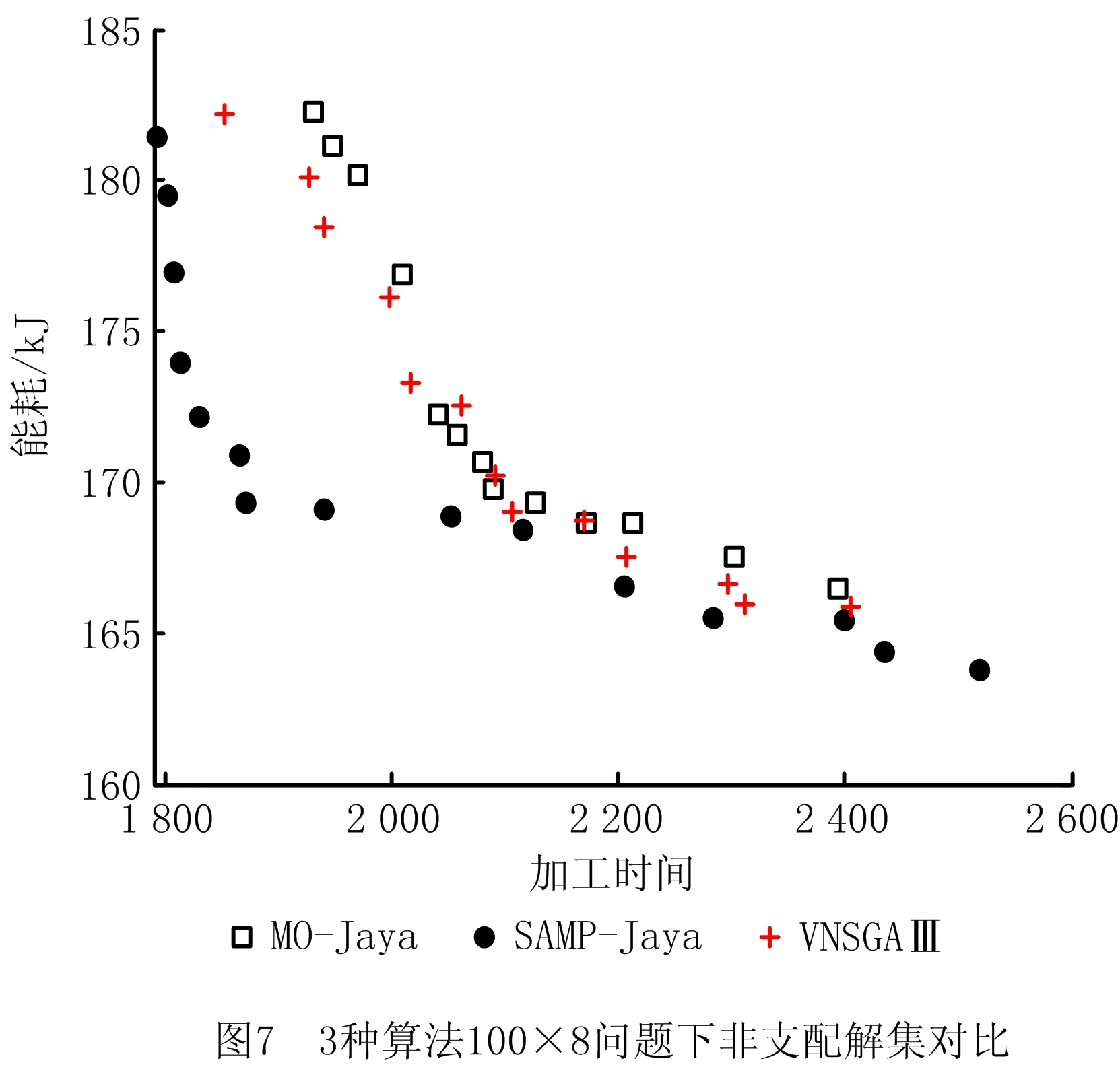
以100×8的问题为例，如图7所示为3种算法所得非支配解集，由图可知，相较其他两种算法，SAMP-Jaya算法所求非劣解集在分布面上更加广泛，分布均匀性更优；MO-Jaya算法获得13个非支配解，SAMP-Jaya算法获得15个非支配，且其极端解均优于MO-Jaya算法，说明所设计自适应多种群策略有助于提升算法的全局搜索能力。

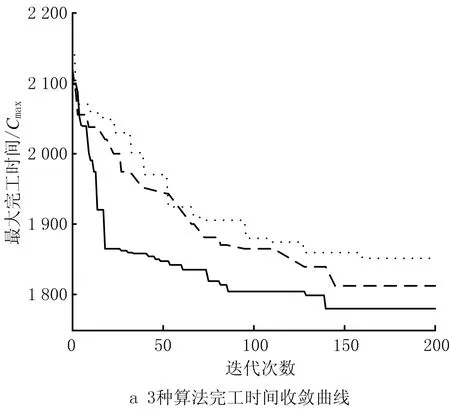
如图8所示为某次运行时3种算法各目标值的收敛曲线。SAMP-Jaya算法、VNSGAⅢ算法、MO-Jaya算法分别在140代左右、145代左右、160代左右时达到最优值；SAMP-Jaya算法的初始解为(2 098,180.25)优于VNSGAⅢ算法、MO-Jaya算法的初始解(2 120,180.88)、(2 150,180.96)，说明所设计多规则初始化种群可以提升初始种群的质量。综上所述，SAMP-Jaya算法两个目标值收敛速度更快，收敛性更为优异。根据图7和图8可知SAMP-Jaya算法的求解质量和收敛性能更好。

4 结束语

在如今提倡绿色制造的生产背景下，本文建立了以最大完工时间和能耗为双目标的带有设置时间的并行机调度模型。针对问题模型，运用一种二维实数编码方案。为有效求解问题，在Jaya算法的基础上设计以下3种策略形成SAMP-Jaya算法：①采用多规则初始化种群来提升初始种群质量；②提出多种群的策略提升算法的全局搜索性与局部开发性，自适应调整子种群数目提升算法收敛速度；③提出位置向量排序机制解决离散型变量更新问题。经过测试分析，从单目标而言，将SAMP-Jaya算法与HGA算法和HDTLBO算法比较，证明了SAMP-Jaya算法的优越性；进而运用SAMP-Jaya算法求解GPMSP-ST，并与MO-Jaya、VNSGAⅢ对比，验证了所设计策略有效地提升了算法求解质量和收敛速度。

未来将从以下几个方面展开进一步研究：①针对如机器故障，订单紧急插入等不确定性因素下对初始调度方案作出调整，形成动态调度；②本文所提种群初始化规则虽然改善了初始种群质量，但效果并不突出，未来可利用启发式规则作进一步改善；③本文问题模型中的工件仅需加工一道工序，针对多工序并行机问题还需深入研究。