基于小波包和反应谱的黄土边坡动力特征研究
2023-02-13梁庆国乔向进王丽丽
王 尚, 梁庆国, 乔向进, 王丽丽
(1. 兰州交通大学 土木工程学院, 甘肃 兰州 730070; 2. 中核四○四有限公司, 甘肃 嘉峪关 735106;3.中国地震局兰州地震研究所, 甘肃 兰州 730000)
0 引言
随着我国经济的发展和对交通基建工程的投入,大量公路、铁路穿越在我国西部的群山峻岭之间。据地震灾害调查显示,汶川地震时就出现了多处滑坡震害现象,地震造成的滑坡损毁道路、桥梁,给灾区的及时救援和物质运输带来了极大困难[1-2]。由此可见,开展黄土边坡在地震动力作用下动力响应特征的研究显得尤为重要。
近年来,国内外学者关于振动台试验已经做了一些研究:杨博等[3]为了研究地震过程中黄土边坡破坏的细观力学过程,以勘察和室内试验为基础,用强度折减法和数值模拟分析地震响应过程中颗粒位移、孔隙率、应力等要素,结果表明:在应力重分布阶段,坡肩处接触力增大,坡体中部土体被持续挤密而剧烈变形,最终滑动面贯通。李福秀等[4]通过振动台试验研究不同强度地震作用下含裂隙与不含裂隙黄土塬斜坡变形稳定特征,结果表明裂隙的存在降低了斜坡的抗震稳定性。王会娟等[5]通过振动台试验研究黄土高原某黄土场地的地震动放大效应,结果表明:在黄土场地中,地震波水平分量放大效应明显,垂直分量有较小的放大效应,PGA随高程增加呈非线性变化,卓越频率向低频偏移,放大系数也呈非线性特性。梁庆国等[6]通过研究大断面黄土隧道洞口段动力特性,得出隧道的抗震设防长度取5倍洞径较为合适。乔向进等[7]通过振动台试验研究桥隧相连体系隧道洞口段的破坏过程,结果表明:洞口段的破坏为拱顶处及以上部位坡面先出现裂缝,而后隧道坍塌。禹海涛等[8]对地下结构抗震中的加速度法进行分析,基于动力时程的方法评价不同工况的适用性,其提出的改进加速度法具有更高的精确性和普适性。许紫刚等[9]基于反应位移法理论总结出了广泛应用于地下结构抗震分析的方法,结果表明:此方法精度高,能在各种断面地下结构抗震中广泛使用。王兰民等[10]对黄土高原地震区滑坡活动规律进行分析,结果表明:地震动强度、地形、地层岩性、土层厚度和地下水等对滑坡活动有重要影响,应对地震高烈度区滑坡进行机理分析、风险评估、防范和治理。许成顺等[11]通过对可液化场地进行振动台模型试验,分析地基土在地震动过程中的破坏现象和规律,结果表明:地震动能量和持续时间越大,液化越明显。李萍等[12]将甘肃省内200多个黄土滑坡作为研究对象,进行极限状态下统计分析和可靠度模拟,研究了滑坡参数与稳定程度的关系。这些研究表明振动台模型试验可以有效再现地震引起的地下结构破坏过程,明确边坡工程等地下结构的震害机理,为地下结构抗震方法的发展起到推动作用。
通过上述分析发现,目前国外内学者、专家对边坡工程动力响应做了大量研究,但对于结合反应分析的纯黄土边坡的振动台试验研究相对较少。黄土边坡工程在我国西部地区广泛分布,且多处于地震高发区,在地震中存在较高的崩塌、滑坡风险。基于此,本研究拟采用小波包和反应谱分析的方法,分析黄土边坡大型振动台模型试验结果及其动力响应特征和破坏机制,以期为同类黄土边坡工程的抗震设防提供一定的参考。
1 小波包方法和反应谱方法简介
1.1 小波包变换过程
小波包分析是基于小波分析的一种信号处理方法。采用小波包分析方法对地震波进行分解时,分解的层数过高或过低均对结果分析不利,小波包分解层数可以根据式(1)确定[13]:
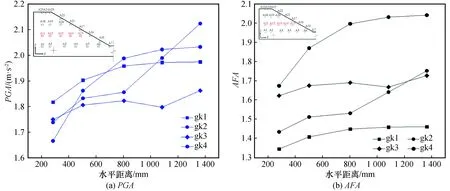
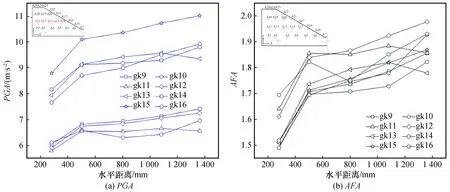
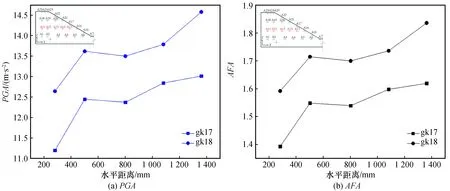
0 (1) 式中:Ls为信号长度;k为分解层数。 采样仪器每隔0.02 s记录一次,信号频率为50 Hz,地震波的持续时间为10~20 s,所以式(1)中的Ls一般是29~210,将其代入式(1)可得k介于0~9之间。在对精细程度进行考虑后,数据后处理时将k取为3[14]。结合Shannon采样定理[15],信号频率要小于采样频率的一半,因此将采样频率定为100 Hz。 小波包基函数的不同在于小波包分析过程中有其各自的优点及适用范围,Daubechies(db)小波具有较好的近似对称性、紧支撑性和光滑性等优势[16],因此优先在地震信号小波包分解中采用。dbN小波包基函数根据N的数值不同分为db1~db10小波,N的数值表示小波的阶数,小波在滤波器中的长度为N的2倍,N值越大,小波光滑性越好。根据本次对地震波信号的处理要求,N取5即可,因此选用db5的小波包基函数。 小波包分析过程中,运用Matlab运行程序,进行测点加速度信号的小波包变换,得出k=3时不同频段的分量,然后提取数据,绘出各频段量的占比图[14]。具体的加速度数据分析过程如图1所示。 图1 加速度数据分析过程Fig.1 Acceleration data analysis process 反应谱是将信号放在单质点系上的一种分析方法,展示了地震动过程中单质点的变化规律特征。反应谱可以记录不同测点的峰值加速度并显示其振动周期,具有较好的时效性,也可以用来探索质点的破坏过程。 试验采用兰州地震研究所大型地震动台,尺寸为 6 m(长)× 4 m(宽),采用刚性半密闭模型箱,其尺寸为2.8 m(长)×1.4 m(宽)×1.8 m(高)。模型设计为黄土边坡,试验用土为按原状黄土∶重晶石粉∶锯末∶水=0.835∶0.04∶0.015∶0.11进行配比后的重塑黄土,采用加速度时程对数据进行记录和分析[14]。 黄土模型边坡高度为96 cm,坡度为45°,坡顶长50 cm。模型采用分层填筑的方法,并逐层压实,在填筑过程中埋设25个加速度传感器,编号为A1~A25。边坡模型示意图如图2所示,图中A0作为参考。 图2 45°边坡模型示意图(单位:mm)Fig.2 Schematic diagram of 45° slope model (Unit: mm) 根据《铁路工程抗震设计规范》[17]和《建筑抗震设计规范》[18]要求,试验选用汶川汤峪波和El-Centro波作为加载波形,加载方式采用X向单向加载和X、Z双向耦合加载,加载过程共有18个加载工况(下文中工况均由gk表示)。 模型试验中,随着加载工况的进行,模型逐渐被震坏,具体破坏过程为:在gk1~gk8(对应的X向加载下加速度峰值XA=0.116g~0.235g)加载过程中,边坡模型上未出现表面可见的裂缝,此阶段定义为弹性阶段;在工况gk9(XA=0.465g)加载之后,在边坡的坡面中间及以上部位,以及边坡两侧开始有裂缝出现,随着加载工况的进行,坡面的裂缝逐渐发展,到工况gk16(XA=0.705g)完成后,坡面中上部位和坡顶几条裂缝逐渐贯通,此阶段定义为塑性阶段;在工况gk17~gk18(XA=0.935g~1.050g)加载过程中,边坡模型有一定程度的震动破坏,坡面与坡顶交界部位有一定的滑塌,坡脚部位出现明显的滑裂面,此阶段称为破坏阶段。具体加载方案和破坏过程如图3所示。 图3 边坡模型加载方案及失稳过程Fig.3 Loading scheme and instability process of the slope model 小波包分析选取模型中部的一组水平测点(A11~A15),提取18个工况下上述测点的E1和E2,E1是加速度信号的第一频段(0.1~6.26 Hz)能量占比;E2是第二频段(6.26~12.51 Hz)能量占比。低频成分(小于12.51 Hz)是主导地震过程中结构物破坏的主要原因,其中E1占主导成分。图4是不同工况下上述水平测点E1、E2变化曲线图。从图中可以看出各测点E1与E2随加载工况的进行呈现“你增我减,此起彼伏”的变化规律,上下部分沿中间水平线大致呈对称分布。随着加载工况的进行,E1呈逐渐增大的趋势,E2呈逐渐减小的趋势。根据图中测点不同工况下E1、E2的突变情况,将整个加载过程分为3个阶段:初始阶段(gk1~gk4),中间阶段(gk5~gk8),后期阶段(gk9~gk18)。由于模型在gk8后才开始出现塑性变形,因此初始阶段和中间阶段都在弹性阶段内。从图4中可以看出,在初始阶段(gk1~gk4),模型的E1和E2转化较为剧烈,原因是此时模型土中各细颗粒处于一个挤压密实阶段,模型内部结构变化急剧,是一个迅速压密的过程;中间阶段(gk5~gk8),模型在前期加载下已趋于密实状态,随着加载工况的进行,模型内部结构基本不变,各测点的E1和E2也变化甚微;在后期阶段(gk9~gk18),模型开始进入塑性阶段,逐渐向大变形至破坏状态过渡,模型内部结构变化急剧,此时E1和E2转化也较为剧烈。如图4所示,前一个阶段进入下一个阶段时,E1会出现突增现象,E2会出现突降现象。gk9下模型开始进入塑性阶段,坡面开始出现裂缝。随着加载工况的进行,裂缝逐渐发展,到gk17、gk18时,裂缝贯通,坡面土颗粒散落,部分塌陷。到gk17下模型进入破坏阶段,E1也出现了小范围突增,E2出现小范围突降。 图4 不同工况下部分测点E1、E2变化曲线Fig.4 Variation curves of E1 and E2 of some measuring points under different working conditions 为研究地震动过程中地震波加载对边坡坡面的影响,选取坡面上6个测点,在初始阶段、中间阶段、后期阶段各选择2个工况,提取各工况下各测点的E1和E2值,并观察其变化规律(表1、表2)。图5是部分工况下坡面测点E1、E2变化曲线图,从图中可以看出3个阶段的6组曲线两两之间有明确的界限和间隔,从而也证明了上述图4所划分阶段的真实可靠性。第一频段能量占比E1随坡面测点高程的增加呈减小趋势,而第二频段能量占比E2正好相反,随坡面高程的增加呈增大趋势,说明E1存在高程的弱化效应,而E2存在高程强化效应。随着加载工况的进行,曲线的倾斜程度变小,说明随着震级的加强,高程对于E1的弱化效应不再那么明显。各测点E1随震级的加强逐渐增大,E2随震级加强逐渐减小;E1最小值为62.79%,而E2的最大值仅为33.49%,依旧说明了E1为主频,E2为次频。 表1 gk1、gk2、gk6下部分测点能量占比 表2 gk7、gk10、gk11下部分测点能量占比 图5 部分工况下坡面测点E1、E2变化曲线Fig.5 Variation curves of E1 and E2 of measuring points on the slope surface under some working conditions 综合考虑,从低频成分能量占比(E1和E2)变化的角度来说,低频部分主要由E1、E2共同构成,所以不能仅从E1或E2单值的大小来判断边坡模型的破坏状态,需要从二者之和的角度出发。除gk2外,其余5个工况下E1+E2的最大值均位于边坡顶部位置,整体最大值出现在gk11下的A25测点(坡顶测点),其值为99.07%,而在实验中模型加载进入塑性阶段后也是先在坡顶位置出现裂缝,从而证明了量化数据分析与试验的宏观表象相契合。这表明在地震动力作用下黄土边坡上部和坡顶位置是最容易产生破坏的位置,建议在施工时应充分重视并加强边坡中上部位以及坡顶位置的抗震设防。 反应谱是边坡内测点加速度、速度随地震波加载时间变化的微观反映,清晰地再现了地震动过程中测点数值的变化情况。由于在岩土材料中只适合进行弹塑性阶段内的研究,因此选取弹塑性阶段的工况(gk1~gk12),对模型中部一组水平方向的测点A11~A15进行研究。图6(a)为不同工况下各测点加速度、速度特征周期的变化规律统计图。从图中可以看出,测点速度的特征周期明显滞后于加速度的特征周期,这也符合相关的物理学现象。前4个工况中,第1、2工况是汶川汤峪波加载,3、4工况是El-Centro波加载,后续每4个工况采用同类加载方式循环加载。12个工况中,汶川汤峪波加载下几个工况的加速度特征周期都维持在0.35 s,El-Centro波加载下几个工况的加速度特征周期都维持在0.46 s,地震动过程中El-Centro波加速度到达特征周期的时间滞后于汶川汤峪波。速度特征周期随工况的变化规律与加速度基本一致,即汶川汤峪波加载下几个工况的速度特征周期都维持在0.96 s,El-Centro波加载下几个工况的速度特征周期都维持在1.01 s左右,地震动过程中El-Centro波速度到达特征周期的时间也滞后于汶川汤峪波。加速度、速度的特征周期随循环加载工况的进行呈现循环变化,在弹塑性阶段,同一类型地震波加载下特征周期不变。 图6(b)是加速度、速度随加载工况变化曲线。从图中可以看出,加速度、速度的变化规律基本一致,都随加载工况的进行大致呈波浪式增大的趋势。在汶川汤峪波和El-Centro波循环加载下,曲线呈倒下的S形循环往复呈现,从初始阶段到中间阶段再到后期阶段变化幅值不断增大。同一阶段内,El-Centro波加载下的加速度、速度值均明显小于汶川汤峪波。图中量化数据显示,在进入不同阶段时曲线有明确突变,同一阶段中相同地震波加载下相邻工况的加速度、速度变化不大。 图6 不同工况下测点加速度、速度特征周期统计及变化曲线图Fig.6 Characteristic periods and change curves of acceleration and velocity of measuring points under different working conditions 综上所述,在加速度达到特征周期时,速度还未达到特征周期,速度的特征周期要滞后于加速度,这也符合物理学相关知识。不同工况下反应谱幅值变化曲线有明确分界,这也与3.1划分阶段一致。随着加载工况的进行,相同类型地震波在不同工况加载下特征周期基本不变,相近地震烈度下El-Centro波的特征周期总是滞后于汶川汤峪波。 为更加明显地展示不同工况下边坡模型水平方向的加速度变化规律,采用传统的研究方法:峰值加速度(PGA)分析和峰值加速度放大系数(Amplification Factor of Acceleration,AFA)分析。选取模型中部的代表性测点A11~A15。由于A16位于坡面上,而在地震作用下PGA及AFA存在临空面放大效应,为了避免临空面放大效应对不同工况下水平向加速度变化规律的影响,分析中不考虑测点A16。分别选取弹性阶段gk1~gk4(XA=0.116g~0.235g)、塑性阶段gk9~gk16(XA=0.465g~0.705g)、破坏阶段gk17~gk18(XA=0.935g~1.050g),对PGA及AFA沿水平方向的变化规律进行分析。 图7是弹性阶段边坡模型PGA及AFA的水平变化趋势图。从图中可以看出,前4个工况下PGA及AFA沿水平方向的变化趋势略有不同,但大致都随加载工况的进行逐渐增大,AFA表现较为明显,在每个工况之间有明确间隔。PGA及AFA沿水平方向随水平距离的增加逐渐增大,增长方式为先快速增长后缓慢增长。模型处于弹性阶段时PGA及AFA总体增幅较小,变化曲线较为缓和;在同一工况下PGA及AFA最大的点均为A15,是最靠近坡面的点。 图7 弹性阶段边坡模型PGA及AFA水平变化趋势图Fig.7 Horizontal change trend of PGA and AFA of slope model in the elastic stage 图8是塑性阶段边坡模型PGA及AFA水平变化趋势图。从图中可以看出,在相同工况下PGA及AFA沿水平方向的变化趋势也是逐渐增大,越靠近坡面的点,其值越大。图8(a)中,PGA在gk9~gk12下变化范围较小,曲线较为缓和,实验中在此工况范围中边坡模型开始出现裂缝,但裂缝较小且发展缓慢。在gk13~gk16下PGA变化范围较大,几乎呈斜直线增长,在此工况范围的模型实验中,裂缝开始急剧增加,且发展迅速至裂缝完全贯通。从图8(b)可见,在AFA沿水平方向的变化趋势中,裂缝出现阶段与裂缝迅速发展阶段分界范围不是特别明显,但曲线的总体变化趋势和PGA相同。 图9是破坏阶段边坡模型PGA及AFA的水平变化趋势图。从图中可以看出,随着裂缝的积累和发展模型开始进入破坏阶段,PGA及AFA在水平方向上增幅较大,且增长的速率不断增大。特别是在gk18中,随水平距离的增加PGA及AFA的增大趋势更加显著,变化幅度更大,此时模型从开始破坏进入到破坏阶段。破坏阶段模型PGA及AFA沿水平方向的变化规律基本一致。 图8 塑性阶段边坡模型PGA及AFA水平变化趋势图Fig.8 Horizontal change trend of PGA and AFA of slope model in the plastic stage 图9 破坏阶段边坡模型PGA及AFA水平变化趋势图Fig.9 Horizontal change trend of PGA and AFA of slope model in the failure stage 综上所述,边坡模型的PGA及AFA存在沿水平方向增大的趋势,即边坡中距离坡面位置越近的点其值越大,越容易破坏。这也与试验现象相契合,试验过程中,边坡坡面处先出现裂缝至最终坡面滑塌,在整个过程中虽然看不到边坡模型内部土体结构的变化,但从量化的数据分析可以验证宏观表象。现实生活中的“鞭梢效应”也可以解释这种情况,即在地震动过程中,由于P波、S波的作用,结构物在前后左右来回摆动的瞬间,越靠近顶端部位的点产生的加速度、速度和位移越大,就像甩动中的鞭子的尖一样。PGA及AFA存在水平向的放大效应,且随震级的加强越来越明显,建议实际工程中加强边坡坡面处的抗震设防措施。 (1) 弹性阶段可细分为初始阶段和中间阶段。初始阶段、中间阶段到后期阶段,加速度信号的第一频段能量占比(E1)和第二频段能量占比(E2)的变化呈现剧烈到缓和再到剧烈的一个过程。E1+E2的最大值位于边坡顶部位置,而实验中模型加载进入塑性阶段后也是先在坡顶位置出现裂缝。 (2) 相同类型地震波加载下,加速度、速度的反应谱幅值随加载工况的进行有所增加;速度的特征周期要滞后于加速度;弹塑性阶段,同种类型地震波不同地震烈度下到达特征周期的时间基本不变,El-Centro波到达特征周期的时间滞后于汶川汤峪波,且前者的加速度、速度反应谱幅值略小,不同工况下反应谱幅值变化有明确界限。 (3) 黄土边坡模型在地震动加载过程中经历了3个阶段:弹性阶段、塑性阶段和大变形破坏阶段;边坡模型在水平方向上存在PGA及AFA放大效应,说明在地震过程中距离坡面越近的位置越容易被破坏和先破坏,这种现象随着震级的加强越来越明显。 (4) 通过试验宏观表象和量化数据的分析,对边坡的动力失稳过程划分了几个阶段,考虑到试验过程的间断性与实际地震过程连续性的差别,失稳过程也难免会有所不同,因此对边坡动力失稳过程的阶段划分尚有待商榷。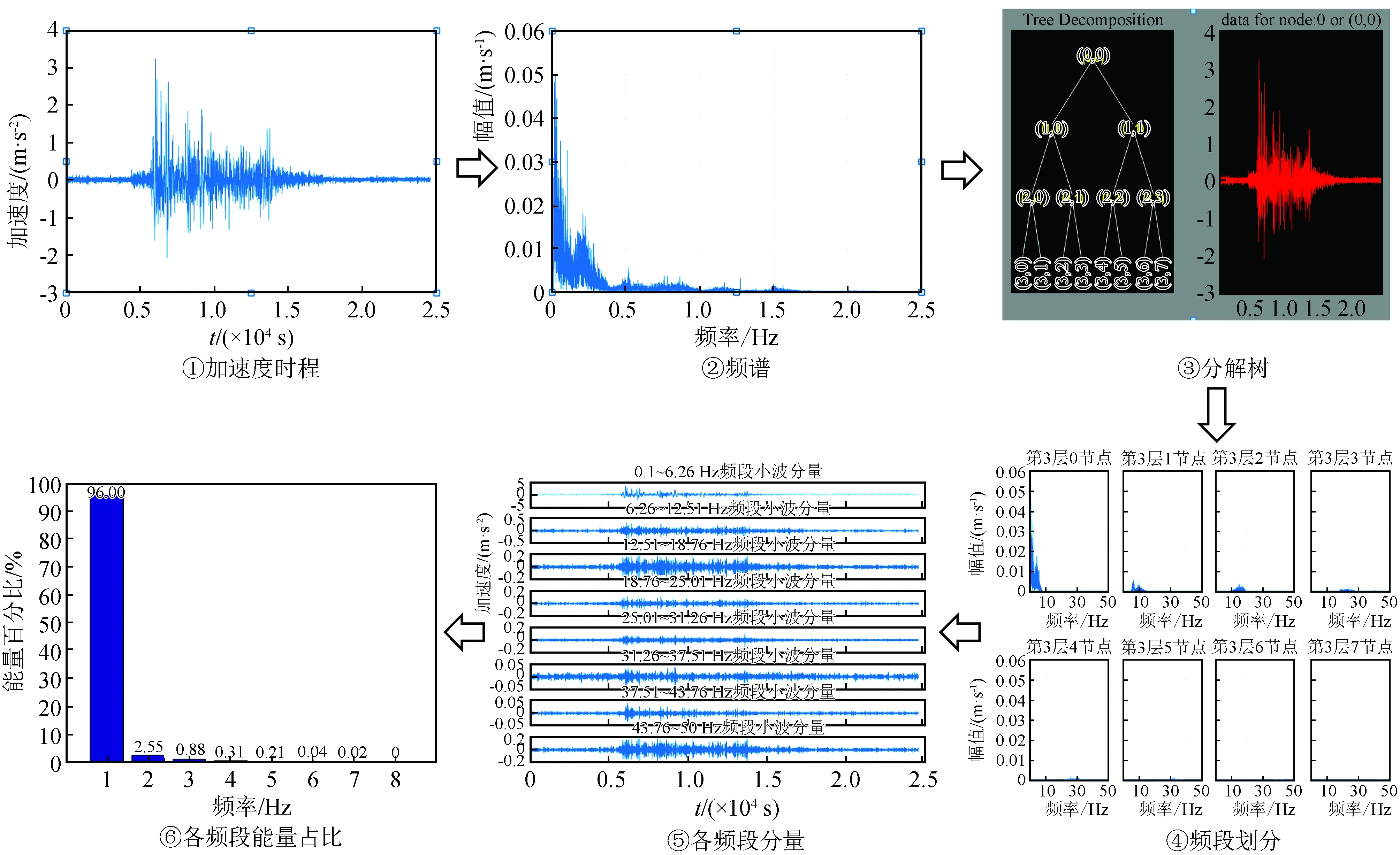
1.2 反应谱方法
2 振动台试验设计
2.1 试验布置及模型填筑
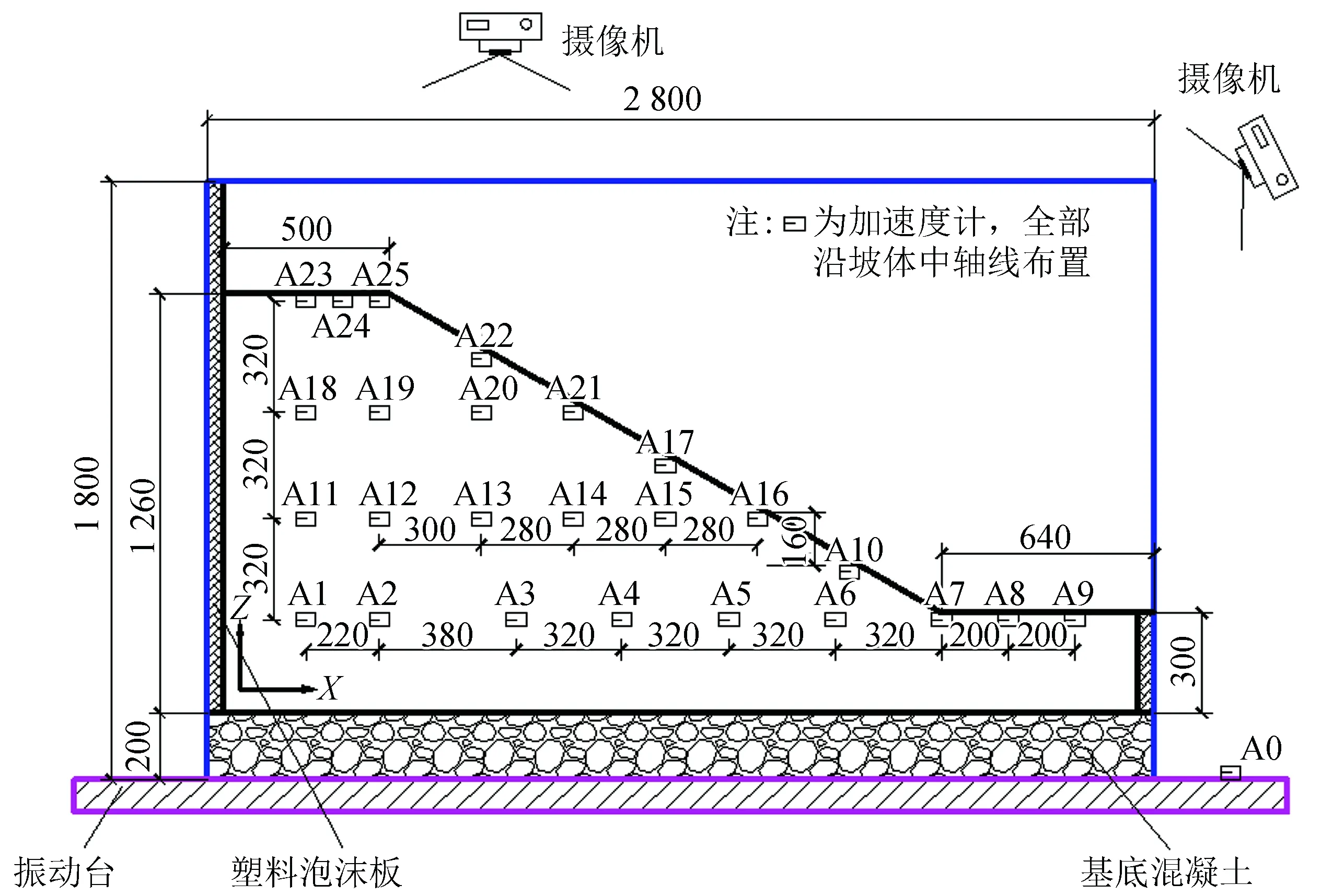
2.2 地震波加载方案与破坏过程
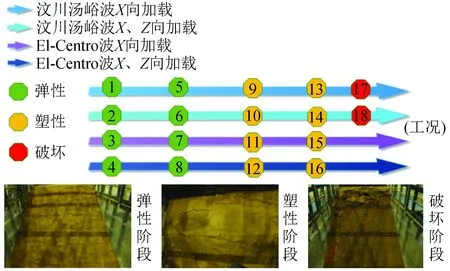
3 试验结果分析
3.1 响应加速度小波包分析
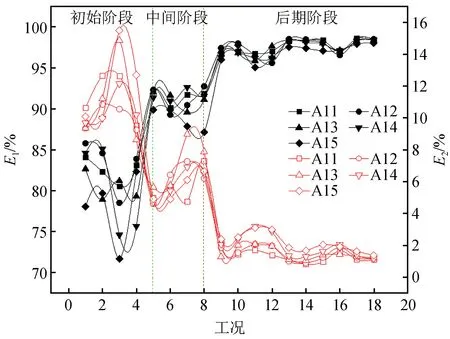
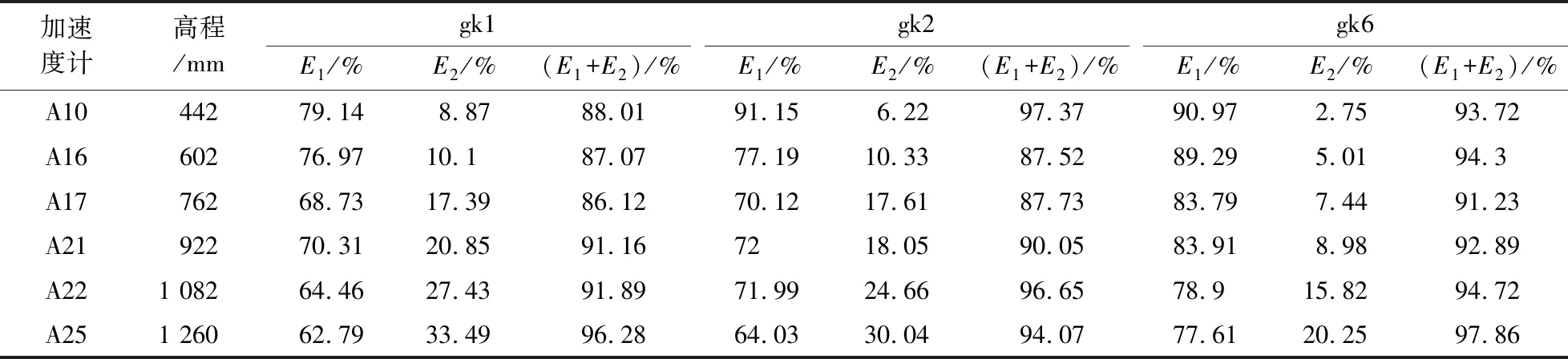
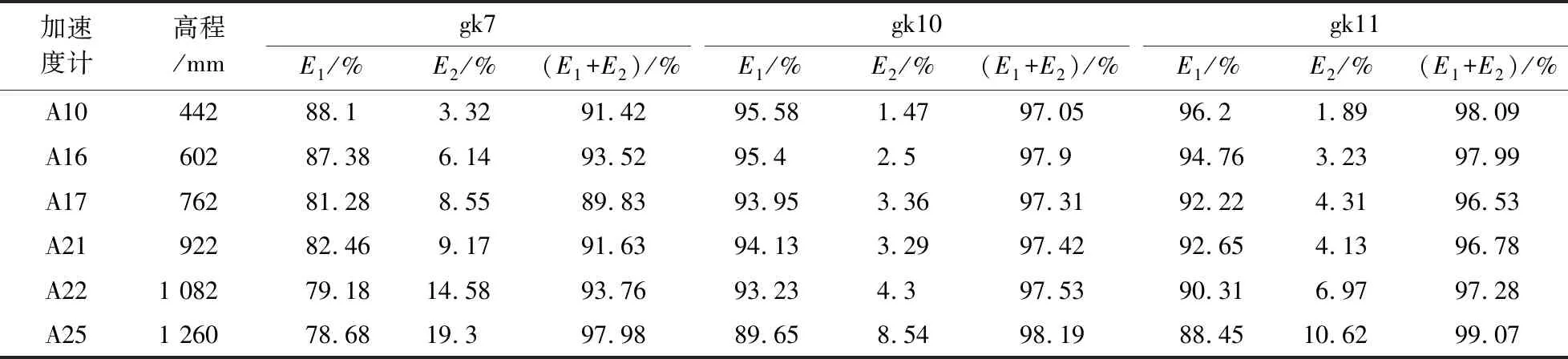
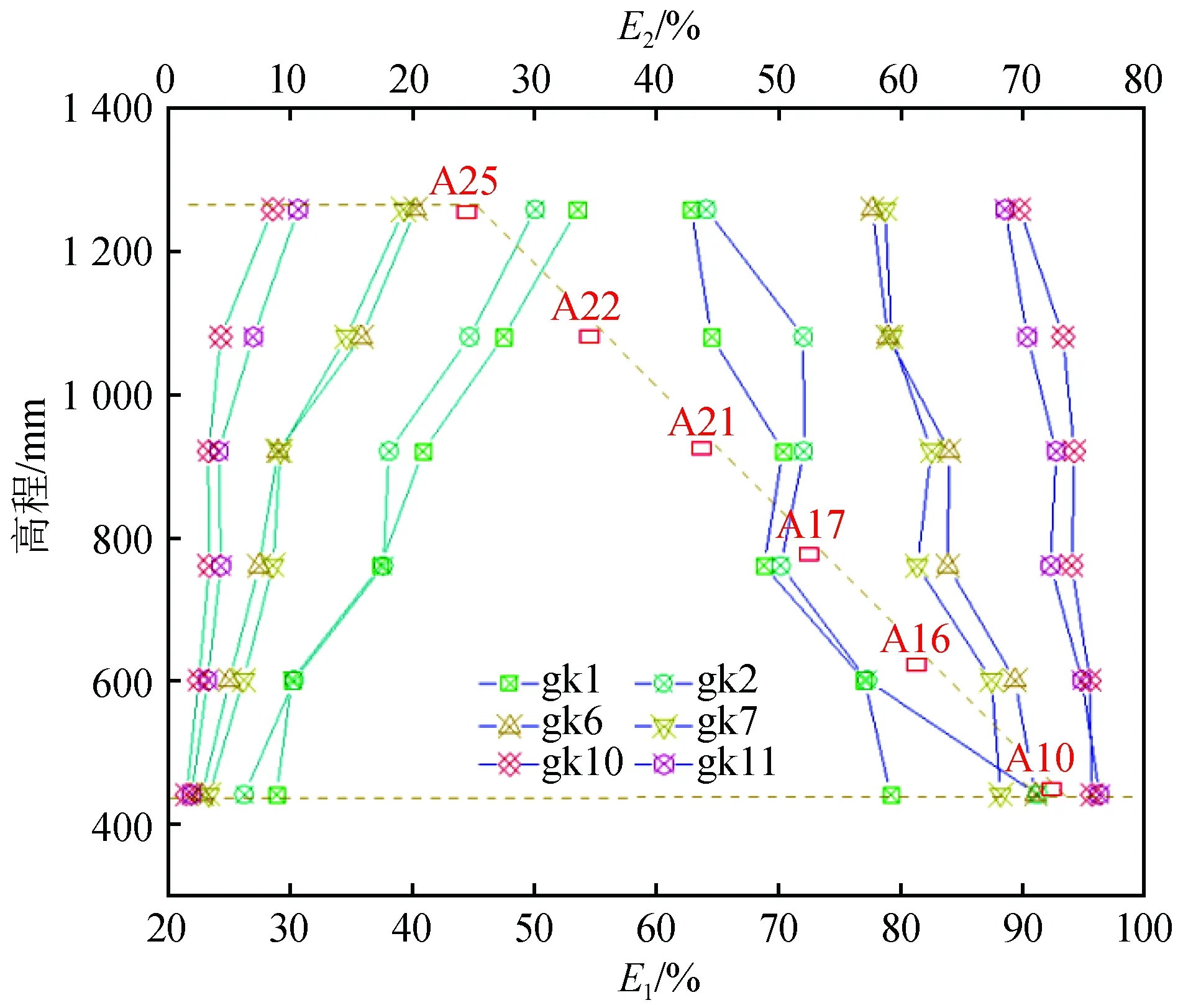
3.2 反应谱分析
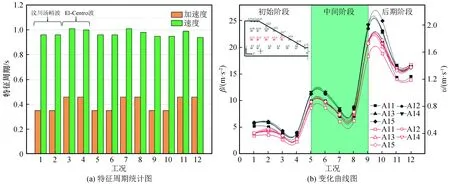
3.3 沿水平方PGA及AFA分析
4 结论
