高速铁路车站岔区高填方路基沉降组合预测研究

2023-02-13马学宁陈玉燕

铁道学报 2023年1期

马学宁，陈玉燕，王旭

(兰州交通大学土木工程学院，甘肃兰州 730070)

目前，我国高速铁路轨道主要采用全线无砟轨道或全线以有砟轨道为主，对于长大隧道或隧道群及其间桥梁常采用无砟轨道的形式。中兰铁路(甘肃段)处于湿陷性黄土区域，大部分车站岔区填方较大、轮轨系统相互作用较强且排水系统较为复杂，存在不均匀沉降影响隐患，且岔区在沉降后日常捣固、垫板起道等维修难度较大。为提高线路稳定性，减少日常维修量，针对中兰客专全线设计有砟轨道的特点，拟对车站岔区有砟轨道进行无砟化。为确定岔区路基工后沉降是否满足铺设无砟轨道要求及无砟轨道铺设时机，需对岔区路基工后沉降进行预测。

迄今，被广泛运用于工后路基沉降预测计算的有经验公式法、灰色系统法、数值模型法[1-4]。高路堤的沉降是与多种影响因素有关的发展过程，它与地基所处的特殊环境、地基土的应力历史、填料的工程性质、路堤的填方高度及施工方法等密切相关，针对不同的侧重点都有不同的预测模型。目前运用最广泛的是灰色系统模型和曲线模型，这类预测模型被称为单项模型[5-10]，每个单项模型的侧重点不同，每一种模型都能为预测提供相应的侧重点的信息。如果人为的选择一种预测模型进行预测，将不可避免的忽略其他一些影响路基沉降的因素，导致预测结果存在片面性[11]。为解决单个预测模型预测精度较低、预测结果存在片面性的问题，学者们试图通过组合模型来综合考虑每个单项模型的有用的信息，来提升预测的精度和可靠性，有些学者将其引入岩土工程领域用来预测路基沉降，目前运用较多的为单一的两模型组合模型[12-17]，即将两个单项预测模型按照某种组合方法进行组合，形成一种新的预测模型，然后将新模型的预测结果与每个单项模型的结果进行对比来分析各模型的优劣性，针对同时建立多个组合模型，平行研究各组合模型的性质的方法却鲜见报道，同时，对于由三个或三个以上单项模型组合的组合模型用于预测路基沉降的方法也鲜见报道。

本文在单项模型的基础上将多个单项模型进行最优组合，形成新的组合模型，可一定程度提高预测可靠性。本文针对中兰高铁某站场高填方路基，结合现场实测沉降数据，分别采用三种单项模型(双曲线模型(H模型)、灰色费尔哈斯模型(V模型)和邓英尔模型(D模型))，和其组合模型(双曲线-邓英尔组合模型(H-D模型)、灰色费尔哈斯-双曲线组合模型(D-H模型)、邓英尔-灰色费尔哈斯组合模型(D-V模型)、三模型组合模型(D-H-V模型))对路基沉降进行预测，并引入多个精度评价指标对每个模型的预测精度进行评价和比对，以期寻求适合车站岔区高路堤工后沉降的最优预测模型，以供此段客运专线或其他类似地段路基沉降预测借鉴和参考。

1 沉降预测模型原理

1.1 单项预测模型

(1)H模型

H模型近似认为路堤总沉降量与时间成双曲线函数的变化关系，可利用双曲线函数对实测的沉降量-时间曲线进行拟合，得到沉降量St随与时间t之间的经验公式，即可求得某个时间对应的沉降量，基本方程式为

(1)

式中：S0为t0时刻路基的沉降量；St为时间t时刻对应的沉降量；α、β为待定常数，可利用线性回归方程采用最小二乘法求解。

(2)V模型

V模型源自于Malthasia模型，Malthasia模型原为预测生物增长的模型，为指数型增长模型，随着生物数量的增多，后期生物繁殖影响因素变多，生物的繁殖速度减慢，生物繁殖呈现出“S”形增长趋势，Malthasia模型无法准确预测生物的后期繁殖。在此基础上，1837年德国数学生物学家对Malthasia模型进行了修正，得到了现在的V模型，为“S”形增长模型，与生物的“S”形增长趋势相符合。路基沉降随时间的变化也表现出“S”形的趋势，所以V模型可用来预测路基沉降随时间的变化关系。

(2)

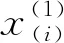
(3)

式中：a、b为待定模型参数，通过最小二乘法求解，具体求解过程见文献[7]。

解微分方程式( 3 )可得

(4)

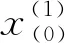
(3)D模型

D模型是由邓英尔在2005年提出的一种预测全过程沉降量的新模型[9]，能大幅度减小预测值与实测值的残差，其基本方程为

(5)

式中：b1、b2、b3、b4均为待求参数，当b4=1时为泊松曲线模型。

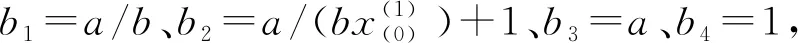
1.2 组合预测模型

组合预测模型的关键是确定各个组成组合模型的单项模型的权重。目前，定权重确定法和变权重确定法是确定单项模型权重的常用方法，因后者在确定权重时过程较为复杂，计算量大，不易操作，因此定权重确定法被优先采用[18-19]。本文在确定组合模型权重时也采用的是定权重确定法。对H模型、V模型和D模型三个单项模型进行最优化组合时，采用定权重确定法，选取目标函数为组合模型误差的平方和最小来求解各单向模型的权重，推导最优加权组合模型，具体建模过程如下：

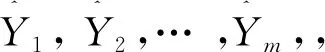
(6)

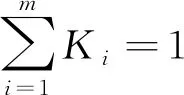
(7)

拟合误差矩阵E为

(8)

式中：i，j=1,2,…,m。

如果记该方法的误差平方和为W，即

(9)

式中：K为由ki所组成的矩阵，k=(k1,k2,…,kn)。

对式(9)利用拉格朗日乘子法求解，由d[KTEK-2λ(RTK-1)]/dk=0，式中R=(1,1,…,1)T，得

EK-λR=0K=λE-1R

(10)

由d(KTEK-2λ(RTK-1))/dλ=0得

RTK=1RTλE-1R=1

λ=1/RTE-1R

(11)

由式(10)、式(11)得最优权重向量为

K0=E-1R/RTE-1R

(12)

2 工程概况及沉降控制补强措施

2.1 工程概况

工点位于中兰客专平川车站，起讫里程DK122+994.15—DK125+053.58，路基以填方通过，最大路堤高度为16.33 m。工点位于山前冲洪积平原区，地形平坦、开阔，现多已开垦为农田，村落稀疏零星分布，地面高程在1 462～1 472 m之间，相对高差为10 m。

2.2 沉降控制补强措施

施工图设计时，该车站选用的轨道类型为有砟轨道。目前，车站两头岔区高路堤地基加固已做完，正在填筑路堤基床底层。结合现场施工情况，为尽量减少铁路运营后出现影响行车安全的路基病害，降低车站岔区路基工后沉降，减少后期养护维修工作量，将岔区有砟轨道变更为无砟轨道。因无砟轨道路基工后沉降控制标准远高于有砟轨道，所以必须在后续填筑过程中对路基进行补强，以便工后沉降能满足铺设无砟轨道要求，具体补强措施如下：

(1)岔区及有砟-无砟过渡段DK123+016—DK123+535及DK124+164—DK124+985正线路堤基床底层范围内横断面方向满铺两层单向高强TGDG120土工格栅，层间距为1.8 m，最下层距基床底层底面为0.3 m。基床以下填料组别及压实标准同基床底层。

(2)基床底层填料施工完成后采用冲击碾压追密，不得低于40遍。

(3)DK123+016—DK123+535及DK124+164—DK124+985段当基床底层顶面冲击碾压完成后，铺设一层复合土工膜(无需设置中粗砂缓冲层)，然后堆载预压，预压高度为3 m，时间不小于6个月，且经过一个雨季。

(4)卸除预压土层，填筑基床表层前，在基床底层顶面铺设复合土工膜进行隔水封闭。

(5)路堤坡脚至排水沟间采用C25混凝土现浇封闭，厚0.12 m。

(6)站场DK123+046.00—DK124+955.278段，基床表层为0.2 m采用级配碎石掺5%水泥+0.5 m的级配碎石填筑，厚度为0.7 m，基床底层厚度为2.3 m，采用B组及以上填料填筑。

2.3 沉降观测

工点范围内从DK123+010起，每隔50 m及路涵过渡段处设置沉降监测断面，沉降观测从2020年4月26日开始至2020年10月23日结束，观测持续180 d，共计观测43次，获得了42个断面的沉降数据。由于篇幅原因，在监测断面中选取填方高度较高的三个断面(DK124+790、DK124+840、DK124+890)路基中心沉降板数据进行分析，各断面实测填土高度-时间-沉降关系曲线见图1。

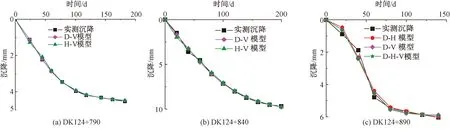
图1 路堤填土高度-时间-沉降关系曲线

由图1可知，三个测试断面随时间及路堤填筑高度的增加，总沉降量逐步增加，呈现出较好的平滑曲线形状，沉降已基本稳定且处于收敛状态。各断面路堤填高分别为11.2、11、11 m，最大沉降量分别为4.5、9.7、6.04 mm，分层填筑完成时各断面的沉降分别为4.0、7.9、5.8 mm，则路基填筑完成时各断面路基沉降量分别为当前总沉降的89%、80%、96%，可见，路基的绝大多数沉降发生在填筑阶段。

3 单项模型预测结果

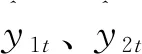
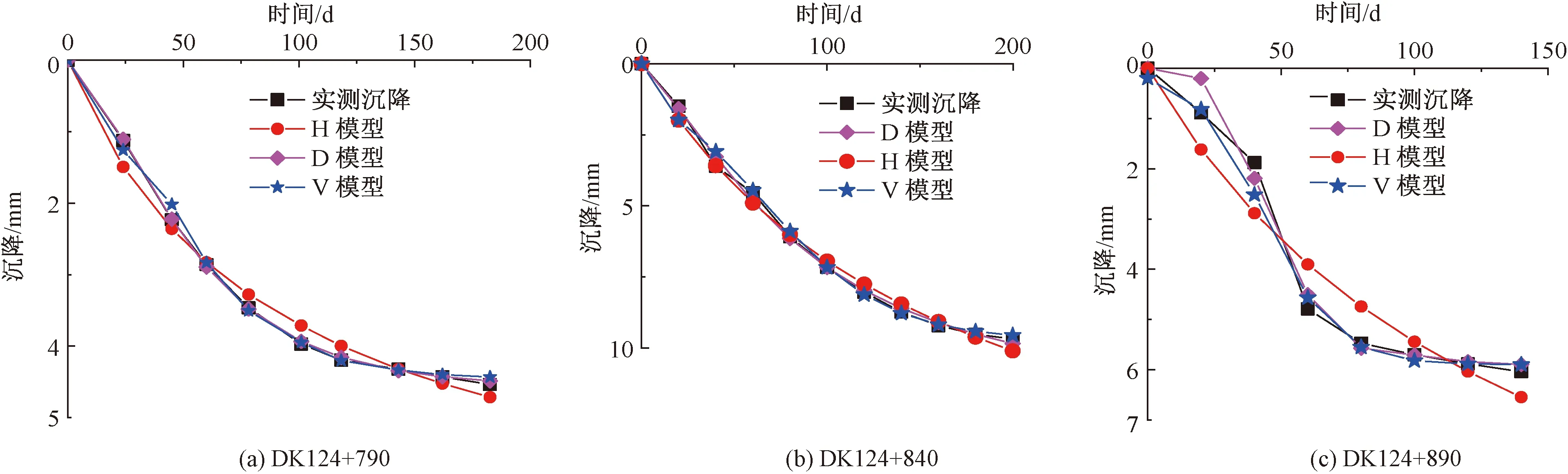
图2 单项模型沉降预测曲线

表1 不同预测模型表达式

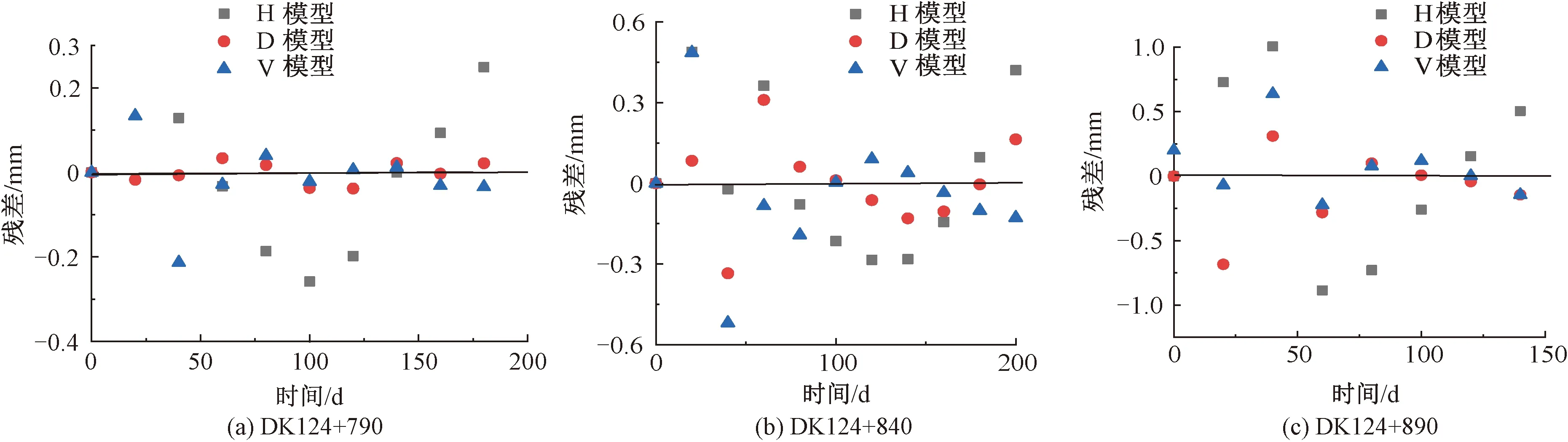
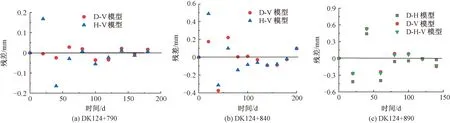
图3 单项模型残差

(13)

依据MAPE值的大小对模型精度预测等级划分表见表2，由式(13)计算各单项预测模型精度指标，见表3。

表2 MAPE预测等级划分

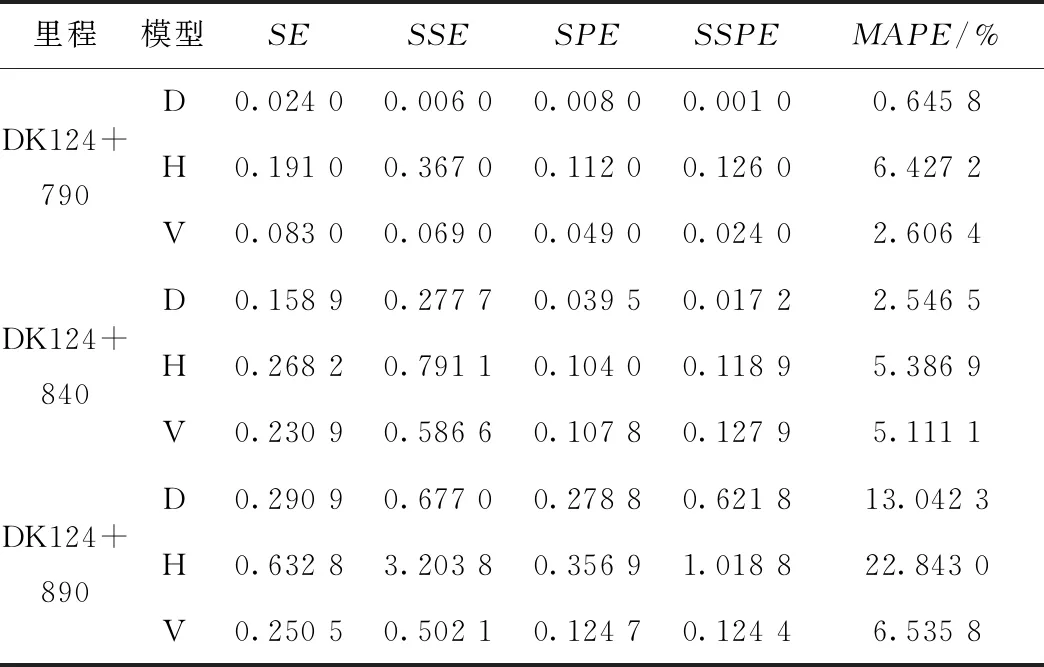
表3 单项模型精度指标

由图2、图3可知，随着时间的增加，三种单项模型在各个时刻各断面处的残差绝对值均小于1，说明三种模型在三个断面处拟合度都较好，H模型前期和后期残差较大，且后期每个断面处的预测值均大于实测值，例如，在最后一个观测点处，在DK124+790、DK124+840、DK124+890三个断面处的预测值比实测值分别偏大了0.25、0.42、0.51 mm。V模型前期残差较大，后期相对较小且V模型残差最大值分布较为规律，均在40 d时，V模型在断面DK124+790、DK124+840及DK124+890上的残差最大值分别为-0.213、-0.519、-0.638 mm。D模型前期在DK124+790和DK124+840断面处残差较小，在DK124+890断面处残差较大，但D模型后期在三个断面处残差都较小，预测曲线基本与实测曲线相重合，预测效果较好。

由表3可知，三种单项预测模型在断面DK124+790、DK124+840的MAPE值均小于10%，预测等级均为高精度预测。在DK124+890断面处，H模型的MAPE值为22.843%，预测等级为可行，D模型的MAPE值为13.042%，预测等级为良好，V模型的MAPE值为6.536%，预测等级为高精度。还可以看出，在断面DK124+790、DK124+840处，无论是SSE、SE还是评价模型稳定可靠性的指标SSPE和SPE及划分模型精度的指标MAPE，均有H模型>V模型>D模型，但在DK124+890断面处，上述各个精度评价指标却表现为H模型>D模型>V模型，结合图2(c)和图3(c)发现，造成DK124+890断面处D模型各精度评价指标大于V模型各精度评价指标的原因是早期邓英尔模型预测误差较大，还可发现，后期D模型残差较V模型小，由于此工程重点在于预测工后沉降，所以前期预测偏差可忽略。综上所述，单项模型预测效果优劣顺序为D模型>V模型>H模型。

4 组合模型预测结果

根据上述组合模型建模原理，将三种单项模型进行两两组合，建立三种新的两模型组合模型，再将三种单项模型同时组合，建立一种新的三模型组合模型。建立两模型组合时令未参与组合的模型的权重系数为0，根据式(12)，求得各组合模型的最优权系数，见表4。

羔羊肉营养丰富，品质上乘，受到众多消费者的青睐。由于其生产周期短，经济效益高受到生产者和市场的广泛重视。特别是肉羊业发达国家，羔羊肉生产己发展成为专门产业，在向企业化、专业化生产和经营格局发展[11]。近年来，青海省为缓解草场退化，重视种羊选育，开始推行羔羊经济，收益甚好，羔羊育肥出栏逐渐引起科技人员和农牧民的重视，以育肥出栏带动加工销售的羔羊产业化悄然兴起。多家龙头企业开始进行规模化、产业化生产羔羊肉。

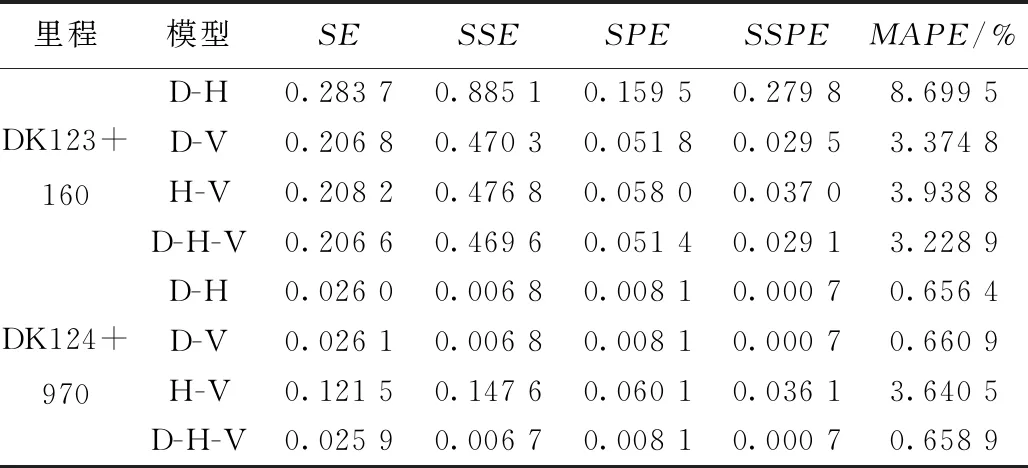
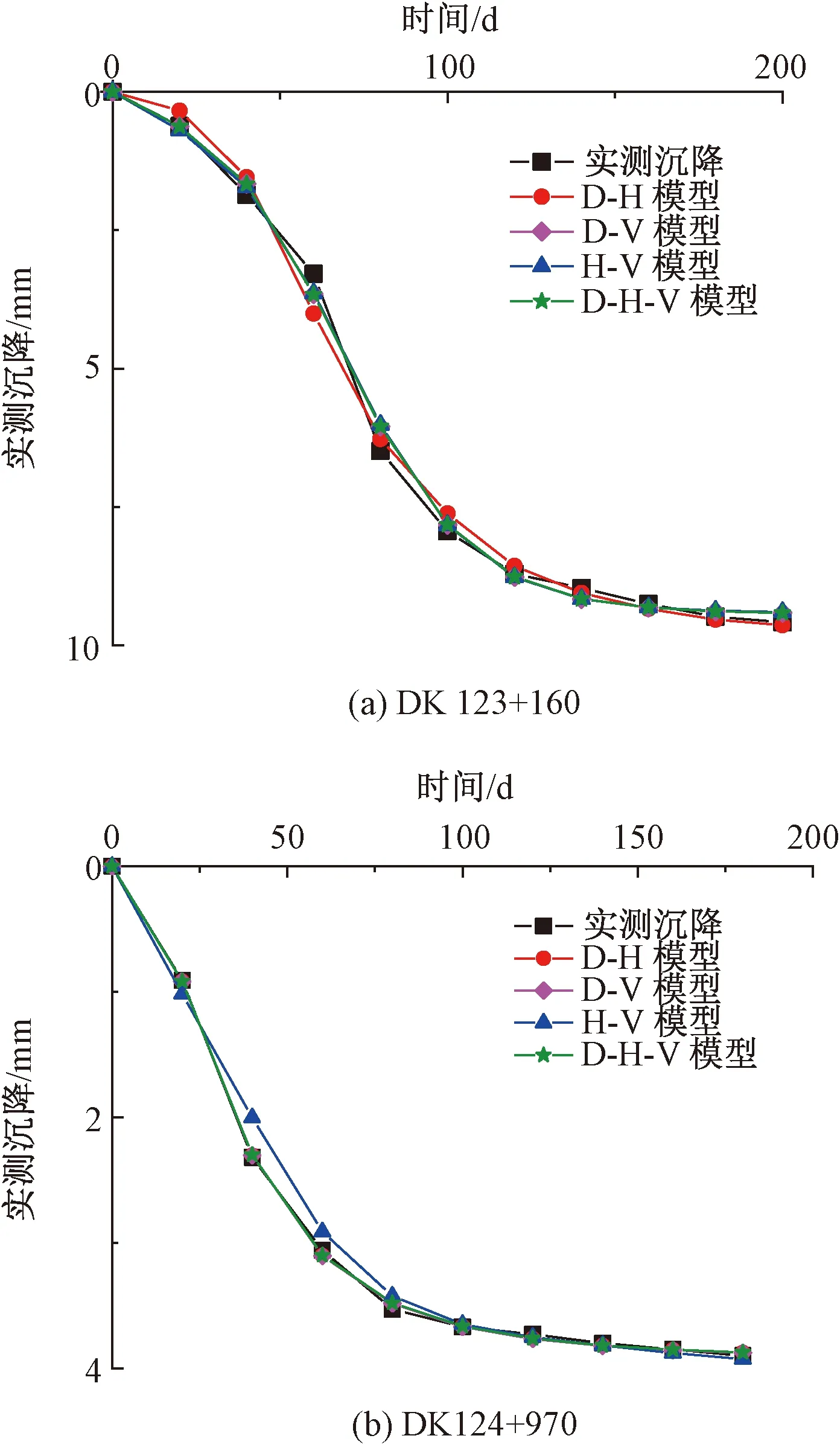
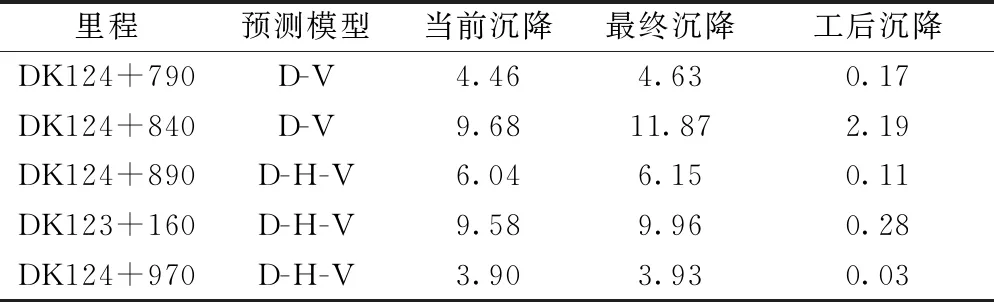
由表4可知，所求出的模型的最优权重系数中存在负值，因负权重是否有意义目前还存在争议，所以此处则认为存在负权重的组合无效，则DK124+790断面和DK124+840断面处有两个有效组合模型，为D-V模型和H-V模型，DK124+890断面处有三个有效组合模型，为D-H模型、D-V模型和D-H-V模型。结合表3发现，单项模型误差越小，组成的组合模型中此单项模型的权重越大，如在DK124+890断面处，D模型、H模型、V模型的残差分别为0.677、3.204、0.502，为V模型

表4 组合预测模型最优权重系数

组合模型预测曲线及其残差见图4和图5，其精度指标见表5。

图4 组合模型沉降预测曲线

图5 组合模型残差

表5 组合模型精度指标

由图4、图5可见，各组合模型在三个监测断面处的残差都比较小，尤其在沉降发展的后期残差基本接近于零，非常有利于预测工后沉降，且除DK124+890断面处的D-H模型的MAPE值为10.106%外，其他组合模型在各个断面的MAPE值均小于10%，均为高精度预测。对比表3和表5发现，任意一种组合模型的SSE和SE总是小于组成此组合模型的任意单项模型的SSE和SE，如在断面DK124+890处，D模型的SSE为0.677 0、H模型的SSE为3.203 8，均大于D-H模型的SSE(0.5323)，D模型的SE为0.290 9、H模型的SE为0.632 8，均大于D-H模型的SE(0.257 9)。由表5还可知，三模型组合模型的误差均小于两模型组合模型，但在本文选取的三个断面处只成功建立了DK124+890断面处的三模型组合模型，仅凭一个断面无法判断结论“三模型组合模型优于两模型组合模型”是否有普遍性，为验证此结论，在所有监测断面中再找出两个能够成功建立三模型组合模型的断面(断面DK123+160和断面DK124+970)，因篇幅有限，此处只给出误差分析结果，见表6。

表6 DK123+160和DK124+970预测精度指标

但要成功建立三模型组合模型的条件较为苛刻，建模不易成功。图6为DK123+160断面和DK124+970断面的组合模型沉降预测曲线。

图6 DK123+16和DK124+970断面组合模型沉降预测曲线

由图4、图6可知，当沉降曲线较平滑，无台阶和转折点时，单项模型和两模型组合模型都能很好的预测沉降，且精度很高，此时三模型组合模型不易建立成功。但当沉降曲线较为复杂(曲线发生转折、陡降或S型等)、规律性差时，三模型组合模型易建模成功，这是因为复杂的曲线较难用一个或两个简单的函数关系式表达，只有通过将不同的简单函数进行组合，才能更好的表达出复杂曲线的线形，这一点也恰好体现出了最优组合模型能够综合利用各单项模型所含信息的意义。

5 工后沉降预测

因高速铁路列车具有运行速度快，对轨下基础沉降要求严格的特点，规范对路基工后沉降提出明确的规定，其中对于无砟轨道路基工后沉降应符合线路平顺性、结构稳定性和扣件调整能力的要求，规定无砟轨道工后沉降不宜超过15 mm。采用各断面的沉降最优预测模型，对5个断面的沉降进行预测，见表7。由表7可见，各断面工后沉降均小于15 mm，符合铺设无砟轨道要求。同理，利用上述方法对其他断面工后沉降进行预测，发现其工后沉降也均小于15 mm，因篇幅有限，具体求解过程此处不再赘述。所以，可认为此段路基工后沉降符合铺设无砟轨道要求。