高速列车受电弓射流降噪仿真分析与风洞试验研究
2023-02-13苗晓丹袁天辰宋瑞刚
郭 璐,苗晓丹,杨 俭,袁天辰,宋瑞刚
(1.上海工程技术大学 城市轨道交通学院, 上海 201620;2.上海工程技术大学 机械与汽车工程学院, 上海 201620)
随着“复兴号”动车组在京沪高速铁路实现速度350 km/h运营,中国高速铁路运行速度成功覆盖200、250、300、350 km/h四个速度等级。高速列车行驶时,噪声主要来源于牵引噪声、轮轨噪声和气动噪声。当车速超过250km/h时,高速气流引发的气动噪声超越其他噪声源成为主导[1]。研究表明,行驶速度达到350km/h时,受电弓区域产生的气动噪声占比高速列车外场噪声源总声压级的7.1%[2]。因此,气动噪声控制是我国高速列车进一步提速所要解决的核心问题之一。
目前,国内外研究学者对受电弓区域气动噪声源特性及噪声控制方法展开了大量研究。文献[3]采用大涡模拟和FW-H方程,探究了湍流场中受电弓杆件的涡结构及气动声学特性。得出受电弓声源强度主要分布在底架、三绝缘子、平衡梁、上臂和下臂等部件,且占总声源能量的92%;影响声源强度的因素包括脱落涡位置、涡流强度以及是否位于涡结构尾流中,这为受电弓气动噪声优化设计提供了参考。针对噪声控制方法,被动降噪技术日趋成熟,例如将受电弓沉降式安装、加装导流板、引入受电弓导流罩设计等,亦或是通过优化受电弓结构外形降低噪声。文献[4]通过IDDES数值模拟和风洞试验相结合的方法,研究受电弓安装平台沉降高度对受电弓区域气动性能的影响,结果表明随着沉降高度增加,空腔前部区域的低速气流域分布变广;涡流吸入来自于车顶两侧的气流,使得作用于受电弓基架及绝缘子的气流速度降低,受电弓的气动阻力减小。文献[5]通过在受电弓两侧增加导流罩的方法来降低受电弓的噪声,并采用碳纤维复合材料对导流罩结构进行铺层设计,实现增加结构强度、刚度并减重的目的。文献[6]利用RNG k-ε模型、大涡模拟及FW-H声类比法对单碳滑板受电弓各部位的气动噪声贡献量、远场传播规律和频域分布规律展开研究,提出对受电弓弓头进行仿生降噪方法,在碳滑板和圆杆上施加前后对称椭球状凸起结构,当碳滑板凸起60 mm、圆杆凸起10.5 mm时,降噪效果最明显,在7.5 m远处整车总声压级降低了2.56 dBA。
然而传统的通过设计合理的结构外形、添加扰流装置或更改物体表面属性来提高列车气动性能的被动控制方法已趋于成熟,未来列车减阻技术主要方向为主动控制减阻,其在航空航天领域得到了广泛应用,成果丰硕[7]。文献[8]通过高速风洞试验,测试了某武器舱舱内的静压分布和脉动压力特性,提出空腔前缘多孔扰流板和前缘吹气两种流动控制变参数研究方法,结果表明吹气位置、吹气流量为流动控制效果的主要影响参数。文献[9]通过高速风洞静态压力测量试验,探究了基于脉冲射流激励器的飞机弹舱气动噪声抑制技术,结果表明空腔前缘布置主动脉冲射流激励器对剪切层施加激励,会改变武器舱上部剪切层的流动特性,对高强度的声载荷有一定的抑制作用。
综上所述,主动降噪技术应用于高速列车噪声控制的研究还较少。本课题组基于高速列车气动噪声主动降噪新方法开展了大量研究。文献[10]初步提出了一种基于射流的受电弓空腔主动降噪方法,得出结论:射流降噪对高速列车节能减排、减阻降噪具有重要意义,且顺向射流降噪效果较为显著。文献[6]进一步分析了复兴号受电弓进行了气动噪声源特性,远场噪声传播规律、频域分布规律研究。在此基础上,为确定最优射流参数,验证射流装置的实际降噪效果,本文通过建立受电弓空腔射流降噪装置,利用数值模拟与风洞试验相结合的方式,探究不同射流速度对空腔噪声的抑制效果。
1 高速列车受电弓气动噪声理论分析
1.1 受电弓空腔噪声发声机理分析
高速列车气动噪声产生于流体与几何体的相互作用或流体的自由运动[11]。一类主要集中在列车壁面的湍流边界层内,由湍流脉动引发;另一类集中在受电弓的圆柱结构,由周期性的脱落涡引发[12]。受电弓区域引发的涡流可划分为三个层:弓头区域、中部铰接区域和底部弓槽区域[13-14]。沉降式(沉降并加装导流罩式)受电弓由于车体表面几何形状突变形成的空腔部位亦为受电弓的重要发声区域。高速气流在空腔前缘产生分离,下沉气体在腔内形成涡流,并经历涡生成、发展与脱落[15]。脱落涡以一定速度向下游移动,与空腔后壁面发生碰撞,并引发向前传播的压力波,此压力波对空腔流动产生自激振荡,形成声波与流动相互作用的反馈回路,使得腔内气流的速度和压力等产生剧烈脉动,诱发强烈噪声[16]。空腔自激振荡示意见图1。
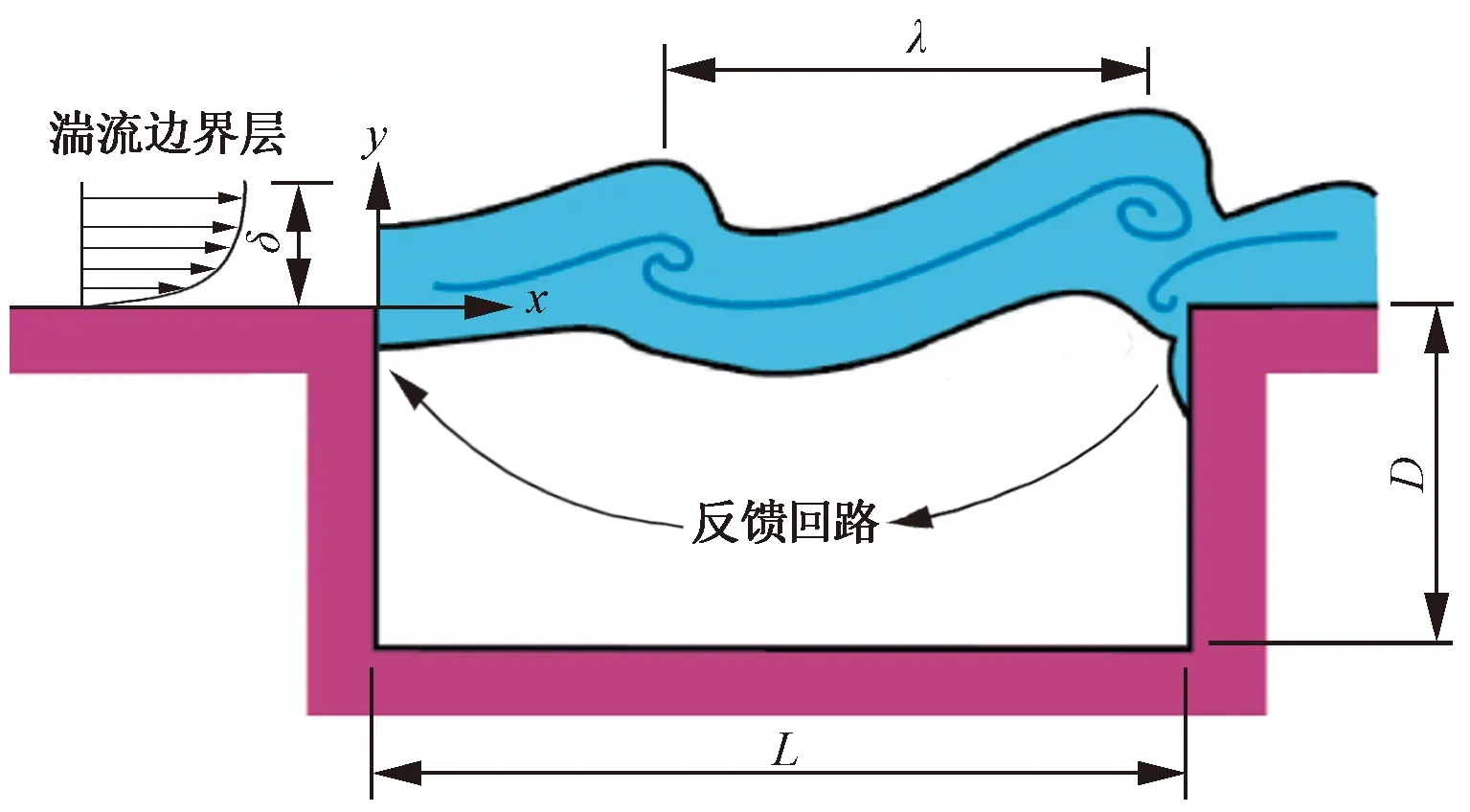
图1 空腔自激振荡示意[8]
1.2 气动噪声模型分析
本文采用大涡模拟LES和FW-H声比拟方程求解受电弓空腔部位湍流流场特性和远场气动噪声规律。大涡模拟解析了含能尺度的涡,通过滤波函数将大尺度的涡和小尺度的涡分离开。在不可压缩定常流动的假设下,用于LES的控制方程是过滤后的Navier-Stokes方程和连续性方程
(1)
(2)

在FW-H声比拟方程中,可将等式右端视作声源项:第一项是流场中湍流应力产生的四极子声源项,第二项是表面脉动压力产生的偶极子声源项,第三项是周期运动产生的单极子声源项。
(3)
式中:c为声速;t为时间;pα为声压;Tij为Lighthill应力张量;Pij为压应力张量;ui为流体在xi方向的速度分量;un为声源表面的法向流体速度分量;vi为xi方向的表面速度;vn为声源表面的法向表面速度分量;δ(f)为Diraclet函数;H(f)为Heaviside函数。
2 受电弓空腔射流降噪效果仿真分析
基于受电弓空腔噪声发声机理分析,建立受电弓空腔射流降噪装置模型。分别采用LES湍流模型和FW-H声学模型对受电弓空腔流场和声场进行求解,并从湍动能、涡量、表面声功率级及远场噪声值等角度分析射流对湍流流场的影响和对空腔噪声的抑制效果,确定最优射流参数。
2.1 几何模型及网格划分
针对含有受电弓车厢段的某和谐号列车进行受电弓空腔射流降噪装置1∶30模型缩比设计。模型包括绝缘子、导流罩、弓槽后壁面以及带有受电弓空腔的车体四个部分,整体外观尺寸为592mm×112mm×79mm(长×宽×高);喷嘴分两排布置在空腔前缘导流罩面板上,喷嘴出口直径d=2mm,见图2。

图2 1∶30射流降噪装置几何模型
计算域见图3,长L=900mm、宽W=320mm、高H=320mm,模型距计算域入口位置L1=188mm、出口位置L2=120mm。计算域入口设定为速度入口(与风洞入口速度保持一致,为40m/s),即:来流马赫数M=0.117;探究的射流速度v=10、20、30m/s;出口设定为压力出口,静压为0Pa;计算域两侧及顶部边界设定为对称面;底部边界设定为固体壁面。
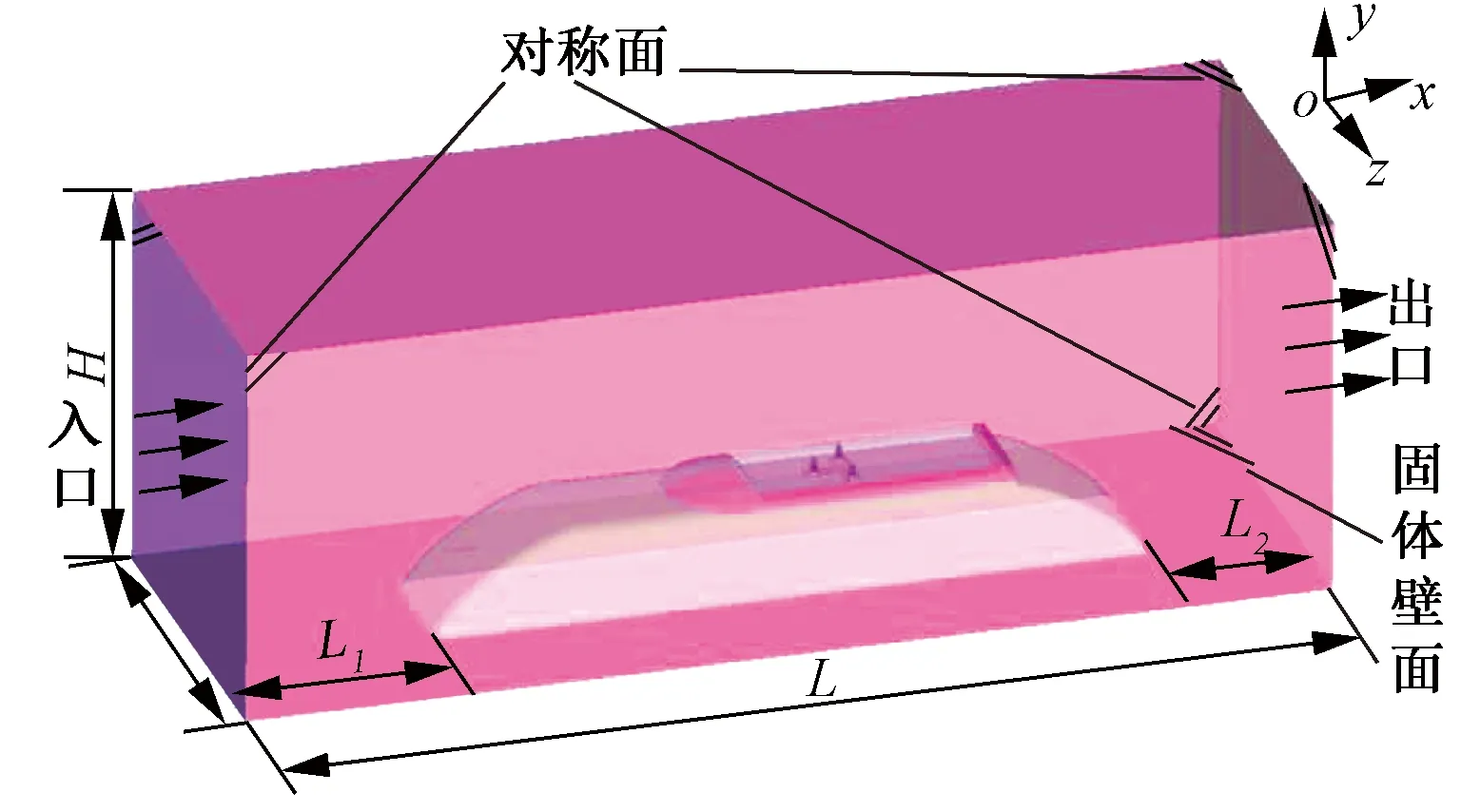
图3 计算域大小及边界条件
为确保网格精度与计算时间,仿真采用混合网格。当总网格数为33 138 683个时,受电弓表面的最大声功率级随网格数目的增加而无明显变化,验证了网格的独立性。具体划分细节包括:子计算域(Block1)采用非结构网格,最小面网格尺寸为0.4mm,位于射流喷嘴与绝缘子处,受电弓弓槽壁面网格尺寸约为0.8mm,子计算域最大面网格尺寸不超过2mm;计算域(Block2)采用结构网格,面网格尺寸约为2mm,见图4。
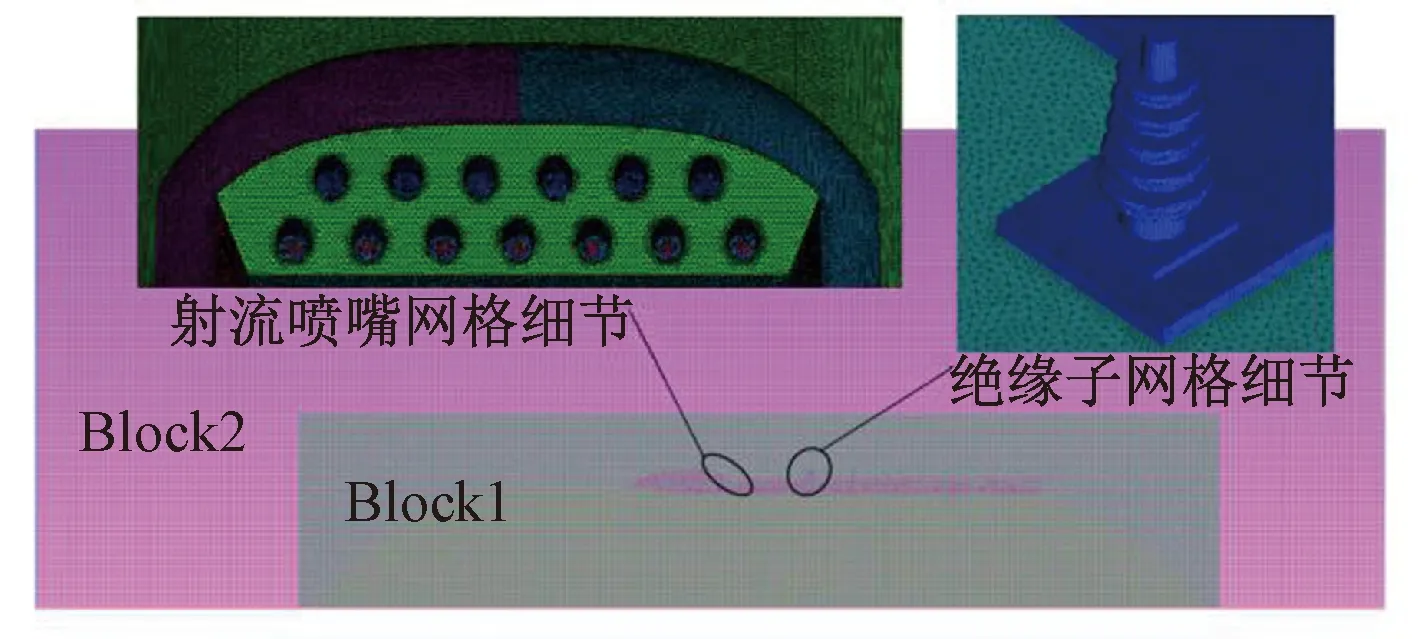
图4 混合网格划分
2.2 求解设置
首先采用标准k-ε模型进行稳态计算,迭代步数为1000步,使得流场充分发展;再进行瞬态计算:采用大涡模拟LES求解湍流流场,时间步长为1×10-4s,时间步数为2000步,每个时间步内迭代20次;采用FW-H声比拟方程求解远场噪声,时间步长为1×10-4s,时间步数为2000步,每个时间步内迭代20次;瞬态计算总时长为0.4s。
参考铁路噪声标准ISO 3095—2013可知远场噪声监测点位置[17],结合本文模型缩比大小,确定两处远场噪声监测点A、B分别位于受电弓弓槽(空腔)几何中心为2.5、8.333m处,距离地面高为1.167m,见图5。
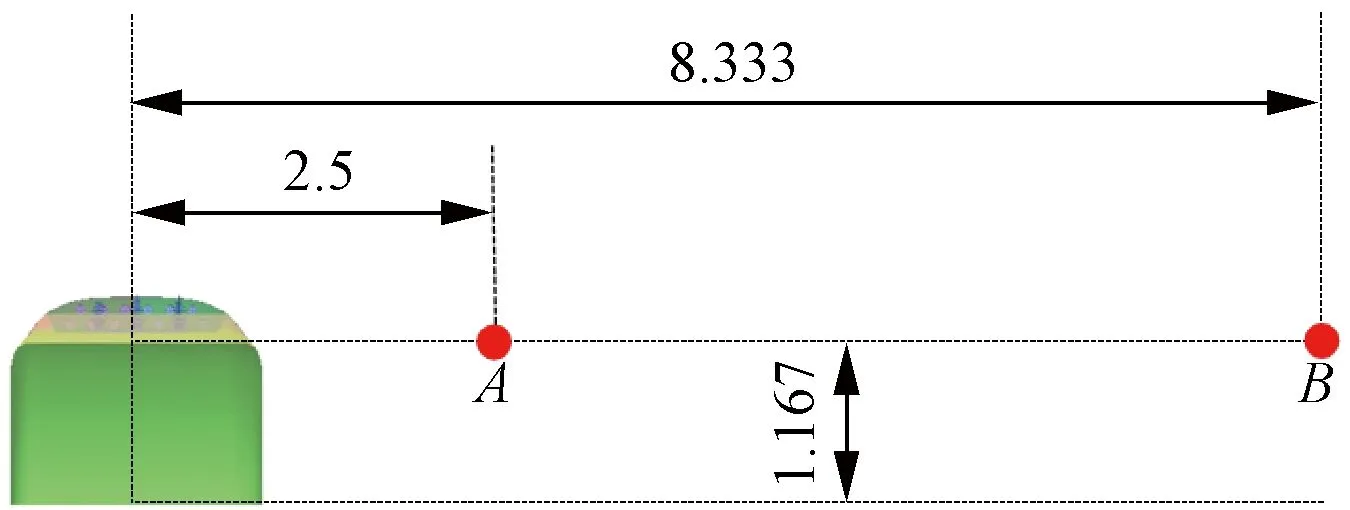
图5 远场噪声监测点(单位:m)
2.3 射流对空腔流场与声场的影响
基于上述空腔发声机理及仿真计算结果,讨论在来流马赫数M=0.117时,不同射流速度(v=10、20、30、40m/s)对空腔噪声的抑制效果,选取湍动能、涡量及表面声功率等物理量,分析空腔流场和声场的变化。
湍动能是表示湍流场中脉动能量的物理量,在一定程度上可以表征声源的分布及强弱[14]。为分析不同射流速度对湍动能大小及位置的影响,在受电弓空腔中部剖面,以弓空腔底部为y轴起点,射流口处为x轴起点建立坐标系,见图6,探究在x/L=5%、绝缘子迎风面、x/L=50%、x/L=95%及空腔后壁面五个站位处,四种射流速度对空腔湍动能的影响(每个站位可测得空腔y方向0~0.03m范围内的湍动能数据,采样点个数为200个)。空腔中间剖面各站位处湍动能曲线见图7。从图7中可以看出:
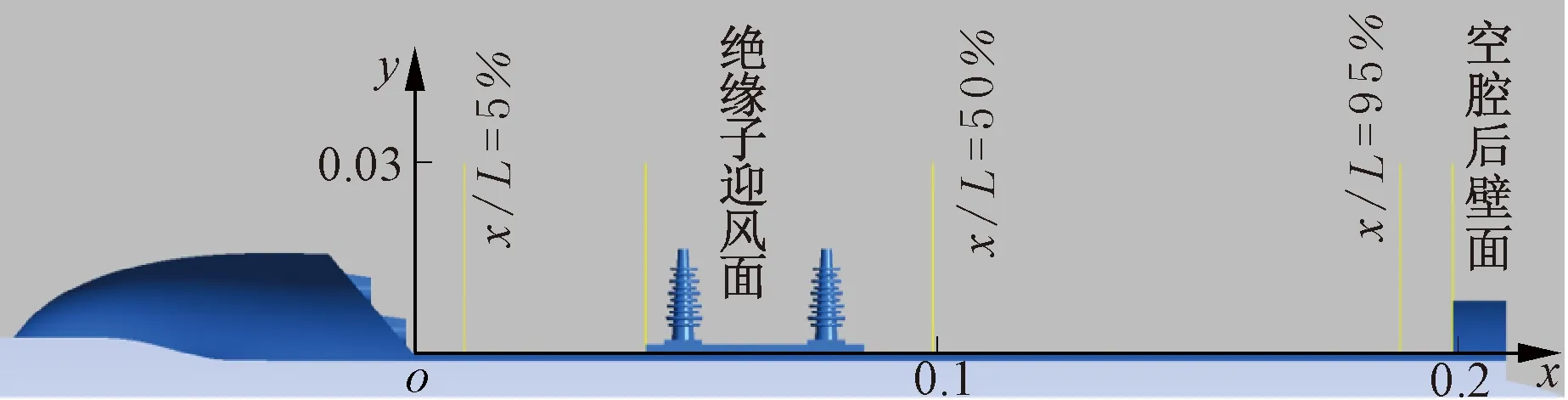
图6 空腔中间剖面各站位示意(单位:m)
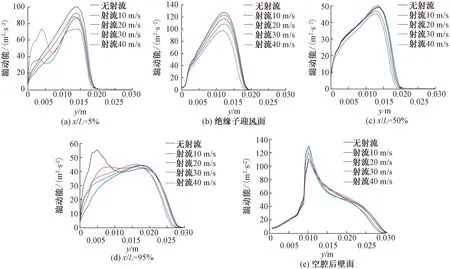
图7 空腔中间剖面各站位处湍动能曲线
(1)在x/L=5%、绝缘子迎风面两个站位处,射流可以降低空腔湍动能,且随着射流速度的增加,湍动能随之减小。在x/L=5%时,距空腔底部上方0.143m处,湍动能最大减小26.68m2/s2;而在距离空腔底部上方0.003~0.004m高度范围内(射流口位置),与无射流相比,射速30、40m/s的湍动能有所增加,这是由射流口处局部能量突增引起。在绝缘子迎风面,距空腔底部上方0.012m处,湍动能最大减小30.51m2/s2。
(2)在x/L=50%站位处,与无射流相比,射速10、20m/s增加空腔湍动能,而射速30、40m/s可降低空腔湍动能;在40m/s射速下,距离空腔0.014m位置处,湍动能最大降低4.63m2/s2。
(3)在x/L=50%站位处,射流增加了距离空腔0.01~0.02m范围内的湍动能,降低了距离空腔0~0.01、0.02~0.03m高度范围内的湍动能。
(4)在空腔后壁面站位处,射流仅增加了距离空腔0.008~0.01m范围内的湍动能,对其他高度范围内的影响不大。
为进一步探究空腔流场复杂湍流运动,以下对涡量进行分析。图8为不同射流速度下,Q准则等值面(Q=0.01)、以速度着色的涡量云图。
从图8(a)中可以看到:(1)受电弓区域主要分布大尺度的涡,较小尺度的涡对流场结构影响很小。(2)在无射流状态下,气体在空腔前缘分离生成涡,而腔内的涡经历了从生成、分离、脱落的过程,这与前述噪声产生机理[15]相吻合,其中腔内包含两种形状的脱落涡,即月牙形脱落涡和带状脱落涡。
由图8(b)~图8(e)可见:与无射流状态相比,在30、40m/s射速下空腔前缘产生的涡更微小、稀疏,分布于空腔后缘的带状涡直径更小;而射速10、20m/s下,腔内涡流并无明显变化。因此,在30、40m/s射速下的流场性能优于在10、20m/s射速下的流场性能。

图8 不同射流速度下Q准则的等值面涡云图
无射流与不同射流速度下空腔表面最大声功率级及其变化见表1。与无射流相比,不同射流速度均可以降低空腔表面最大声功率级,当射流速度为40m/s时,表面最大声功率级可降低4.503 dB。
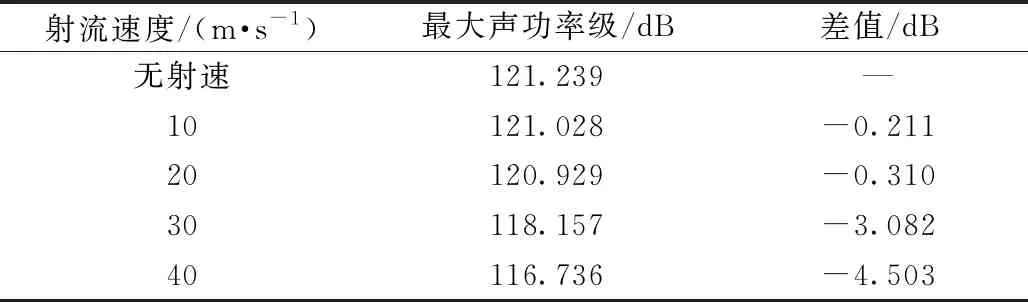
表1 不同射流速度下空腔表面最大声功率级
图9为无射流与射速40m/s情况下表面声功率级云图对比。
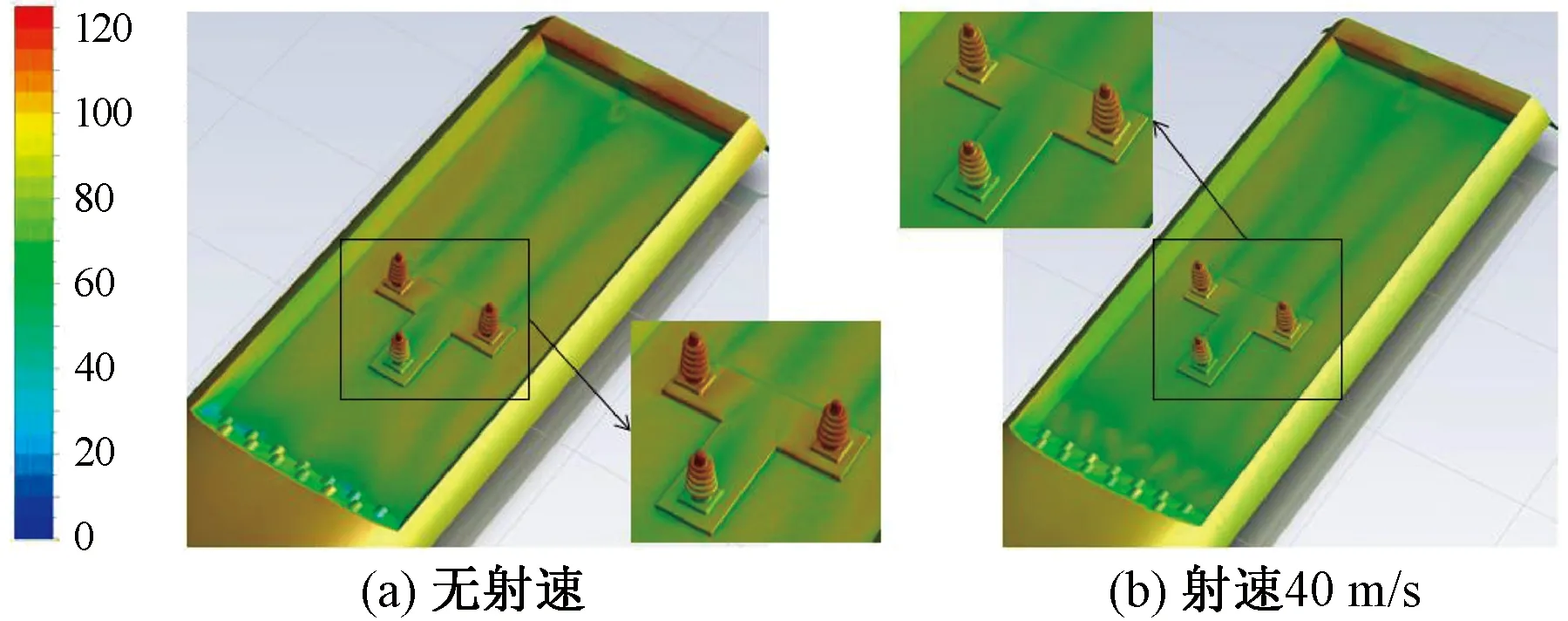
图9 表面声功率级云图对比
由图9可以看出:
(1)受电弓空腔表面最大声功率出现在绝缘子迎风面和空腔后壁面,进一步分析:来流气体与绝缘子迎风面直接碰撞,运动至空腔下游时,与空腔后壁面发生再次碰撞,气体粒子与固体壁面的相互作用,因而产生较大的噪声。
(2)与无射流相比,在40m/s的射流速度下,绝缘子迎风面最大声功率有所降低,空腔后壁面最大声功率级有所降低,且受电弓区域最大声功率出现位置即为空腔后壁面,从而可以认为受电弓区域表面最大声功率级是减小的,这与表1中的结果一致。
不同射流速度下,远场接收点A(8.33m)、B(2.5m)两处的噪声值,见表2。与无射流状态相比,射速10、20m/s在接收点A、B处的噪声值均有增加,而射速30、40m/s在接收点A、B处的噪声值降低;当射流速度为40m/s时,接收点A处有噪声最大减小值1.43 dB,接收点B处有噪声最大减小值1.16 dB。因此,30m/s为来流马赫数M=0.117时的最优射流速度,可实现射流对空腔噪声的抑制效果。
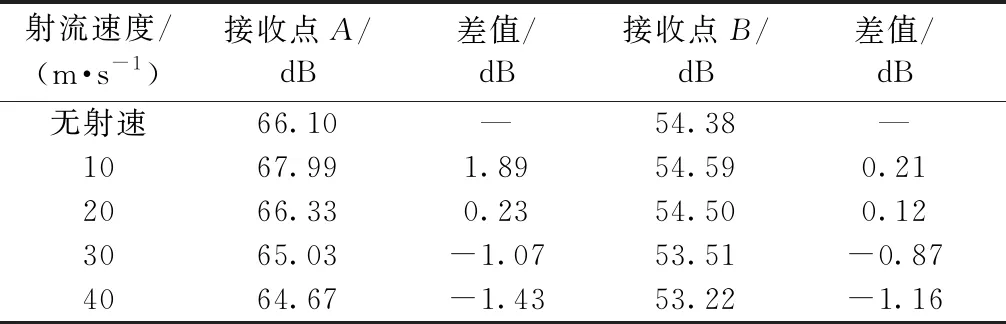
表2 不同射流速度下远场接收点A、B两处的声压级
综上分析湍动能、涡量、表面声功率级及远场噪声值,可以得出:射流速度接近于来流速度时,可实现射流对空腔噪声的抑制效果;且射流速度与来流速度保持一致时,降噪效果最佳。通过射流增加空腔前缘的局部能量,减缓气体下沉,提高了剪切层的稳定性,改善了腔内流场的湍流脉动情况。
3 1∶30缩比风洞试验验证
利用射流装置实物模型进行1∶30缩比风洞测压试验,测试空腔后壁面处的脉动压力。将数值模拟和风洞试验中的脉动压力数据进行傅里叶变换,获取脉动压力频谱特性曲线。根据总声压级分析射流前后、仿真值与风洞值的误差,验证本文气动噪声计算方法的准确性。
3.1 风洞平台及供气设备
HL3-2A-5A型低速风洞结构组成包括收缩整流段、装置安装段(试验观测段)以及扩散保护段;试验段腔体截面为正方形,截面面积为0.32m×0.32m,试验段腔体长度为0.9m,侧边开设一个长0.5m、宽0.3m的可开闭式门,用于被测物件的放置;最大试验马赫数M=0.147。在试验中[18],模型的长度小于试验段长度的70%,模型最大迎风面积与风洞试验段横截面积之比ε=9.5%,试验阻塞比处于阻塞效应不敏感区,这一区域的阻塞比小于10%[19]。
射流装置的气源采用VA-65型空气压缩机,排气量为0.08m3/min,额定排气压力为0.7/0.8MPa。空压缩机依次与调压阀、通气软管和导流罩气腔相连接,将气体引入至射流喷嘴。
3.2 测试设备及数据处理
试验选择测量湍流流场的脉动压力作为间接评价降噪效果的物理量,脉动压力与噪声值总声压级的关系为
(4)
(5)
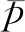
脉动压力测点布置在受电弓空腔(弓槽)后壁面上,包括后壁面中心位置(Point1)、边缘位置(Point2),见图10。
图10 脉动压力测点布置
测点的脉动压力通过德国汉姆HM91微型压力变送器测得,传感器测头直径为4.5mm,量程为-15~15kPa,输出信号DC 0~5V (三线制),测量精度为±0.5%FS,工作时需24V直流电源供电;利用AVANT MI-7016数据采集与信号分析仪采集处理数据,采样频率24kHz,采样时间10s。
3.3 误差分析
由第2节中数值模拟分析可知,射流速度为40m/s时,有最优降噪效果。以下选取无射流与射速40m/s两个案例,通过对比数值模拟与风洞试验监测得到的脉动压力数据,验证本文模型的计算结果。
将风洞试验和数值模拟中的脉动压力数据进行傅里叶变换,图11、图12显示了在300~5 000 Hz的频率范围内,监测点Point1和Point2分别在无射流和射速40m/s下脉动压力频谱特性曲线。由图11、图12可以看出:仿真与试验结果中压力的脉动幅度和降低趋势差别不大,验证了本文气动噪声计算方法的准确性;而在中低频率范围内(300~3200Hz)仿真的脉动压力大于风洞试验值,在高频范围内仿真的脉动压力大于风洞试验值。这是因为:数值仿真中选择的湍流模型为大涡模拟模型,无法精确捕获到小的涡结构,且略微高估了马赫数M=0.117处的大涡能量。
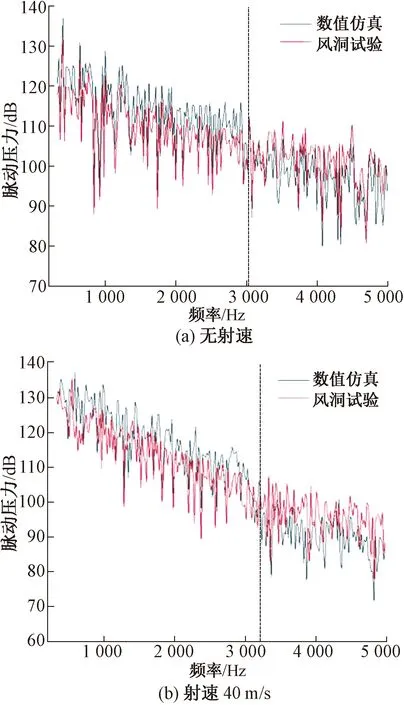
图11 监测点Point1处脉动压力频谱特性曲线
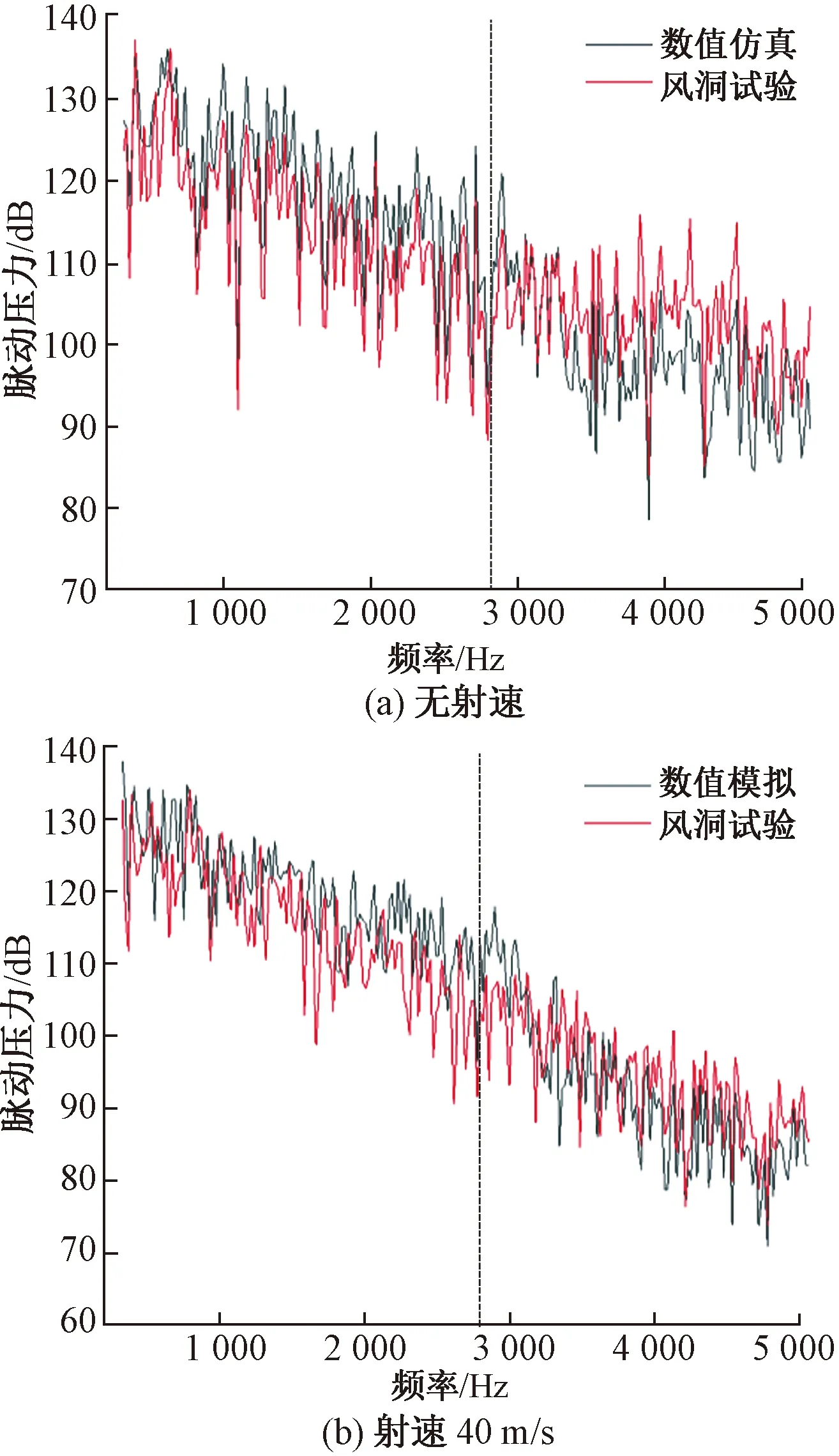
图12 监测点Point2处脉动压力频谱特性曲线
根据式(4)、式(5)计算出各监测点射流前后噪声值的总声压级OASPL,见表3。监测点Point1和Point2处总声压级仿真值与试验值的最大误差为3.54 dB,接近于文献[20]提出的高速列车复杂模型风洞试验的3 dB误差大小。与无射流相比,监测点Point1处总声压级的仿真值减小了1.09 dB,测试值减小了0.53 dB;监测点Point2处总声压级的仿真值减小了0.81 dB,测试值减小了0.49 dB。由于试验中存在壁面效应,未对脉动压力数据进行洞壁干扰修正,因而测试的降噪值与仿真的降噪值存在一定差距。
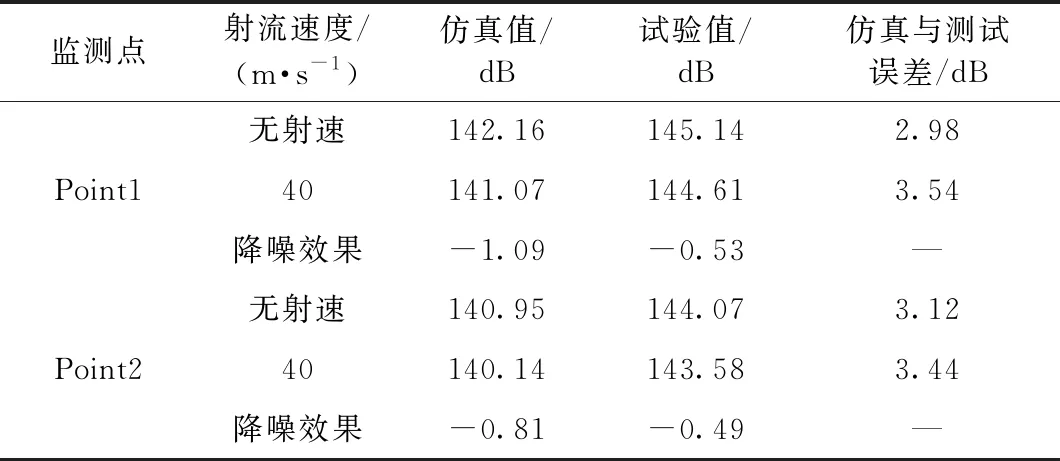
表3 监测点Point1、Point2处总声压级OASPL变化
4 结论
本文通过数值模拟,以空腔前缘无射流情况为参考,比较了不同射流速度(10、20、30、40m/s)对受电弓空腔流场和声场的影响,并进行了风洞试验验证,得到了以下结论:
(1)通过对比分析射流降噪模型的数值模拟结果与风洞试验验证及其他学者的计算结果,证实了本文所采用的LES湍流模型和FW-H声学模型能够准确地捕捉流场结构特点和计算声场噪声值,其仿真得到脉动压力在不同频率的变化规律也能够很好的吻合风洞测试数据。
(2)本文所设计的射流降噪模型能有效降低空腔噪声,其中射流速度为40m/s时,受电弓空腔表面最大声功率级降低了4.503 dB,远场噪声值在2.5m接收点处降低了1.43 dB,在8.333m接收点处降低了1.16 dB,达到了降噪设计目标。
(3)空腔的降噪效果与湍流脉动的剧烈程度有关。射流提高了剪切层的稳定性,抑制了湍流场中分离涡、脱落涡的产生,减少了与空腔后壁面碰撞的剧烈程度。
