石英包体拉曼偏移压力计
—— 一种变质压力计算方法
2023-02-13王美慧张立飞
王美慧,张立飞
(北京大学 造山带与地壳演化教育部重点实验室, 北京 100871)
高压变质作用研究对于揭示俯冲带的地质演化历史具有重要意义,而准确计算变质岩石的温度压力条件是确定是否发生高压变质作用的基础。目前,确定岩石变质温度压力条件的主要方法是基于矿物成分的热力学计算,如矿物对元素平衡温压计(Merecier, 1976; Krogh Ravna and Terry, 2004)、变质相平衡模拟(魏春景等, 2009; Whiteetal., 2014)等。然而, 俯冲带折返的高压-超高压岩石往往由于后期退变质作用叠加的影响,矿物发生不连续反应或者变质重结晶作用使峰期变质组合被抹掉,从而阻碍了传统热力学温压计对峰期变质条件的可靠估计。此外,矿物在高温高压变质条件下,其光谱振动属性(如拉曼光谱)会随着温度压力发生系统的偏移,因此,高温高压下矿物的光谱学振动特征可以用于确定其环境温度压力条件。激光拉曼光谱是一种可以在不破坏样品的情况下识别矿物微小包体的有效工具(Wangetal., 1999; Gilletetal., 2002; Zedgenizovetal., 2004)。通过激光拉曼位移标定矿物包体在常温常压下保留的残余压力,结合包体与寄主矿物的弹性物理特性(压缩性和膨胀性),能够定量约束包体被捕获时的温度压力条件。该方法是基于矿物物理性质的,基本不受化学平衡的约束,因此是示踪俯冲带受后期退变质改造的高压-超高压岩石形成条件的有效方法(Schimidt and Ziemann, 2000; Enamietal., 2007; Korsakovetal., 2009; Ashleyetal., 2014a; Kouketsuetal., 2014)。
目前,该矿物物理光谱学压力计已经被广泛用于不同的包体中,如金刚石-镁铬铁矿(Nestolaetal., 2019)、石榴子石-磷灰石(Ashleyetal., 2017)、石榴子石-锆石(Zhongetal., 2019)、绿帘石-石英(Cisnerosetal., 2020)、金刚石-蓝晶石(Nestolaetal., 2018)、金刚石-橄榄石(Nestolaetal., 2011)、金刚石-柯石英(Sobolevetal., 2000)、锆石/石榴子石-柯石英(Parkinson and Katayama, 1999)等。Nestola等(2019)应用金刚石-镁铬铁矿矿物对弹性压力计首次确定了俄罗斯西伯利亚金伯利岩中含镁铬铁矿金刚石的物源深度,其工作原理即将X射线衍射和傅里叶变换红外光谱数据与矿物的弹性模型相结合,从而获得包体的捕获压力。金刚石-镁铬铁矿体系在使用过程中局限性相对较小,因为: ① 金刚石的塑性变形相对较小; ② 镁铬铁矿晶体接近圆形,“几何效应”小(Mazzucchellietal., 2018); ③ 金刚石与镁铬铁矿均为立方体对称,近似弹性各向同性,而金刚石与镁铬铁矿间存在的流体边问题,则因其厚度很小,可以忽略(Nimisetal., 2016)。Ashley等(2017)提出了利用石榴子石中的磷灰石包体作为地质温压计的新模型。该模型评估了磷灰石964 cm-1特征峰的温度和压力敏感性,结果表明,磷灰石包体较小的特征峰偏移可能不太适合光谱测压法,尽管如此,磷灰石压力仍可以通过峰期拟合进行解析和量化。在温度敏感性方面,磷灰石的964 cm-1特征峰对于高温下的压力测定具有适用性,如在热液金刚石压腔中。而在应用锆石等温度敏感性较高的矿物包体计算压力时,则必须考虑温度的影响。同时,加热实验表明,基于磷灰石的弹性各向同性模型在计算捕获压力时不需要进行较大校正,但关于磷灰石复杂的化学成分对拉曼峰偏移的影响还需要进一步的研究。
石英作为一个近乎纯的端员,其拉曼峰偏移主要受到压力和温度的影响(Schmidt and Ziemann, 2000),且由于石英相对常见,寄主矿物石榴子石具有更高的可压缩性,当压力发生较大变化时,两者之间会保留较大的压力差,这种压力差会被拉曼位移所记录,因此石英包体弹性拉曼压力计是个潜在的地质压力计(Hemley, 1987;Schmidt and Ziemann, 2000)。目前已有几种石英包体弹性拉曼压力计的计算方法被提出,如EosFit-Pinc(Angeletal., 2017)、QuIB-calc (Ashleyetal., 2014b)、EntraPT (Mazzucchellietal., 2021)和Kohn (2014)发表的算法等。本文详细介绍了石英包体拉曼压力计的原理和计算方法,并利用4种不同的石英包体拉曼压力计[关系图法(Kouketsuetal., 2014)、EntraPT(Mazzucchellietal., 2021)程序、QuIB-calc(Ashleyetal., 2014b)、Eosfit-Pinc(Angeletal., 2017)]对石英包体样品进行计算,结合计算结果及不同方法的特点,总结了不同方法的适用条件与局限性。这对后续研究选择合理的石英包体拉曼压力计具有指导意义。
1 石英包体拉曼压力计的原理和方法


图 1 室温室压下α-石英的标准拉曼光谱(据Kouketsu et al., 2014)Fig. 1 Representative Raman spectra of α-quartz at atmospheric pressure and room temperature (after Kouketsu et al., 2014)
不同的矿物具有不同的压缩性和膨胀性,当包体被寄主矿物捕获并完全包裹后,随着温度和压力的变化,它们会表现不同的体积变化,此时在包体内部存在残余压力(Rosenfeld and Chase, 1961; Howelletal., 2010)。残余压力指在消除外力作用后,物体内部仍存在的保持自身平衡的内应力,它受温度、压力、矿物自身特性及相变影响(Rosenfeld and Chase, 1961; Barronetal., 2008)。矿物包体作为天然形成的封闭体系,与人工形成的金刚石压腔体系具有相似性,因此可以在高温高压实验条件下,利用金刚石压腔定量标定矿物包体拉曼频移压力计。Schmidt和Ziemann(2000)在静水压力场条件下,利用热液金刚石压腔测定了石英在23~800℃、0.1~2.1 GPa之间拉曼峰的偏移。结果表明, 石英206 cm-1特征峰的偏移与温压之间不存在明显相关性, 而464 cm-1特征峰的偏移则与压力呈拟线性关系, 石英包体的拉曼偏移随压力的增加而系统地增加, 斜率为9 cm-1/GPa, 在600℃以下没有观察到等温线斜率对温度的依赖性。在23℃等温线上, 石英拉曼谱峰的偏移与压力之间的函数关系(Hemley, 1987)可以用下列方程式表示:
p=0.360 79×(Δνp)4642+110.86(Δνp)464
(1)
其中,ρ为包体的残余压力(MPa); 0 cm-1<(Δνp)464≤20 cm-1;t=23℃。
而464 cm-1特征峰的偏移则与温度呈轻微的非线性负相关, 因此为扩大公式的适用范围, 消除温度对拉曼峰偏移的贡献, 需进一步通过内插法对温度进行校正:
(Δνt)464, p=0.1 MPa=2.501 36×10-11t4+1.464 54
10-8t3-1.801×10-5t2-0.012 13t+0.29
(2)
该式中t为温度(℃); Δν为拉曼位移(cm-1)。
捕获压力不等同于残余压力,而残余压力受控于包体被捕获时的温压条件和矿物的弹性物理特性(Zhang, 1998; Izraelietal., 1999)。因此,Kouketsu等(2014)基于矿物热弹性模型和数值模拟计算了石英被捕获时的温压条件与室温室压下残余压力的关系。首先基于线性弹性理论,利用包体与寄主矿物的相对体积变化,通过数值模拟确定体系的残余压力(Gilletetal., 1984; Zhang, 1998; Guiraud and Powell, 2006),其关系式为:
Vh(p,t)/Vh(p0,t0)=Vi(pi,t)/Vi(p0,t0)-
3(pi-p)/4μ
(3)
其中,p=0.1 MPa,t=25℃,pi代表室温室压下的残余压力(GPa);p0代表包体被捕获时的压力(GPa);t0代表包体被捕获时的温度(℃);h代表寄主矿物;i代表包体;V代表体积(cm3);μ为寄主矿物的剪切模量(GPa)(Guiraud and Powell, 2006)。然后利用状态方程(Holland and Powell, 1998)计算石英和铁铝榴石的体积,公式如下:
V(p,t)=V(0.1 MPa, 25℃)[1+α0(t-25)-20α0
4p]}1/4
(4)
其中,α0为热膨胀参数(K-1);p代表包体被捕获时的压力( GPa);t代表包体被捕获时的温度(℃);V代表体积(cm3);k为25℃时的体积模量(GPa)。将方程(4)代入方程(3)即可从捕获时的变质条件估计常温常压下的残余压力,再结合残余压力与拉曼位移的关系(Schmidt and Ziemann, 2000)获得石英拉曼光谱位移与任意温压条件的关系图(Kouketsuetal., 2014),通过这一关系图可以快速恢复变质信息。
2 不同石英包体拉曼压力计的特点分析
相较于将矿物的弹性参数设为常数的模型, Kouketsu 等(2014)提出的方法在利用石英和石榴子石状态方程计算残余压力时, 考虑了压缩性和膨胀性对温度和压力的依赖, 避免了根据残余压力估计变质压力的弹性模型过于简化而可能造成的压力误差。另外, 不同于仅通过464 cm-1拉曼峰的位移来确定残余压力, 利用ω和Δω来定义拉曼光谱的位移程度, 降低了可能的系统误差。同时, 根据构建的压力-温度-拉曼位移关系图(图2), 可以直观的分析测量到的残余压力及定量计算其变质压力, 省去了单独计算弹性参数或体积的需要。

图 2 石榴子石中石英包体的压力-温度-拉曼位移关系图(据Kouketsu et al., 2014)Fig. 2 Pressure-temperature-Raman shift diagram of quartz inclusion in garnet in the range of 0.1 MPa to 2.6 GPa at 25~600℃ (the grey areas represent the negative residual pressure ranges, after Kouketsu et al., 2014)
该关系图法的应用是基于包体和寄主矿物都是弹性各向同性及包体是孤立球体的假设,在这种条件下,包体处于一个均匀的静水压力场。然而自然界存在的矿物都是弹性各向异性的,包体实际上受到的是非静水压力场(Eshelby, 1957; Murrietal., 2018; Mazzucchellietal., 2018, 2019),因此包体拉曼位移与静水压力条件下的不同(Anzolinietal., 2018; Thomas and Spear, 2018)。Bonazzi等(2019)利用高温高压活塞圆筒实验证明,高压条件下,石榴子石中的石英包体在遭受各向异性的应变后会产生一个偏应力,从而使残余压力的偏差高达0.7 GPa; Murri等(2019)通过理论计算模拟也发现,非静水压力场下存在一个偏应力,这时基于静水压力场条件下对残余压力和捕获压力的估计不准确。采用声子模格鲁内森张量,应用stRAinMAN软件及EntraPT程序(Grüneisen, 1926; Barronetal., 1980; Angeletal., 2019; Murrietal., 2019; Mazzucchellietal., 2021)可以对非静水压力场条件下的残余压力进行校正,限定石英包体被捕获时的温压条件,正确解释石英的拉曼位移。
石英包体的拉曼位移随寄主矿物成分的不同而发生系统性变化,其拉曼位移与寄主矿物的弹性参数(体积模量和剪切模量)之间具有正相关关系 (Enamietal., 2007),不同矿物或同一矿物的不同端员的弹性参数具有较大差别(Wang and Ji, 2001)。在大多数模型中, 均假设石榴子石弹性模量参数为纯端员组分(铁铝榴石),然而天然石榴子石是一个由不同端员组成的固溶体矿物,在某些情况下这会导致计算出的压力具有偏差(>0.1 GPa, Ashleyetal., 2014b)。QuIB Calc程序采用一个简单的理想混合规则,使端员成分的弹性特性与它们的相对含量成比例混合,近似天然石榴子石组分的弹性模量参数,减小了计算误差(Ashleyetal., 2014b)。
在寄主-包体矿物体系中,计算残余压力的经典方法是基于矿物的线性弹性性质推导的(Eshelby, 1957),然而随着压力或温度的变化,两相矿物的弹性性质不是一个常数,这需要用非线性EOS状态方程来表达。此外,在俯冲带高压-超高压岩石的折返过程中,由于外界温压条件的变化或构造应力的作用,岩石体系将发生强烈塑性形变或脆性断裂,导致具有超压的包体矿物发生弹性弛豫,从而影响对包体温压条件的计算(Yamamotoetal., 2008; Korsakovetal., 2010)。Angel等(2017)建立了EosFit-Pinc软件,该程序给出了矿物的非线性EOS状态方程与弹性弛豫问题相结合的精确计算方法。
3 不同石英包体拉曼压力计的比较
本文利用4种不同的石英包体拉曼偏移压力计[关系图法(Kouketsuetal., 2014),EntraPT (Mazzucchellietal., 2021)程序, QuIB-calc(Ashleyetal., 2014b),Eosfit-Pinc(Angeletal., 2017)] 对来自西藏松多变质带的榴辉岩(Zhangetal., 2022)、新疆西天山哈布腾苏变质带的石榴角闪岩以及Bonazzi等(2019)榴辉岩相条件下合成的两种铁铝榴石中的石英包体进行了包体捕获压力计算,用合成实验和相平衡模拟获得样品的标准温压值分别为775℃、3.00 GPa, 800℃、2.5 GPa, 539℃、1.84 GPa和570℃、1.75 GPa(图3)。这4种计算方法分别考虑了矿物压缩性和膨胀性对温度和压力的依赖、弹性各向异性石英包体对非静水压力场的影响、寄主矿物成分对压力的影响及弹性弛豫对包体残余压力的影响。从图3中可以看出,对于样品Alm-1和Alm-2,由关系图法和QuIB-calc方法计算得到的压力偏高,其偏差最大可达0.90 GPa;由EntraPT程序计算得到的压力则偏低;最大偏差可达0.55 GPa;而由Eosfit-Pinc程序获得的计算结果则与标准值吻合度较高。样品Alm-1和Alm-2的峰期温度较高,在折返过程中可能会促使具有超压的包体发生弹性弛豫,引起应力释放,而Eosfit-Pinc程序基于非线性状态EOS方程对矿物包体压力计进行了弹性弛豫校正(Angeletal., 2017),这可能是导致不同压力计结果不同的原因。对于样品XL10和H17,其峰期温度较低, 受到弹性弛豫影响可能较小,然而自然界存在的矿物晶体都表现出弹性各向异性(Eshelby, 1957),同时天然寄主矿物往往具有混合的固溶体成分(Wang and Ji, 2001),这会导致计算的石英包体残余压力有较大差别,因此由Eosfit-Pinc获得的计算结果较其他3种方法误差更大。
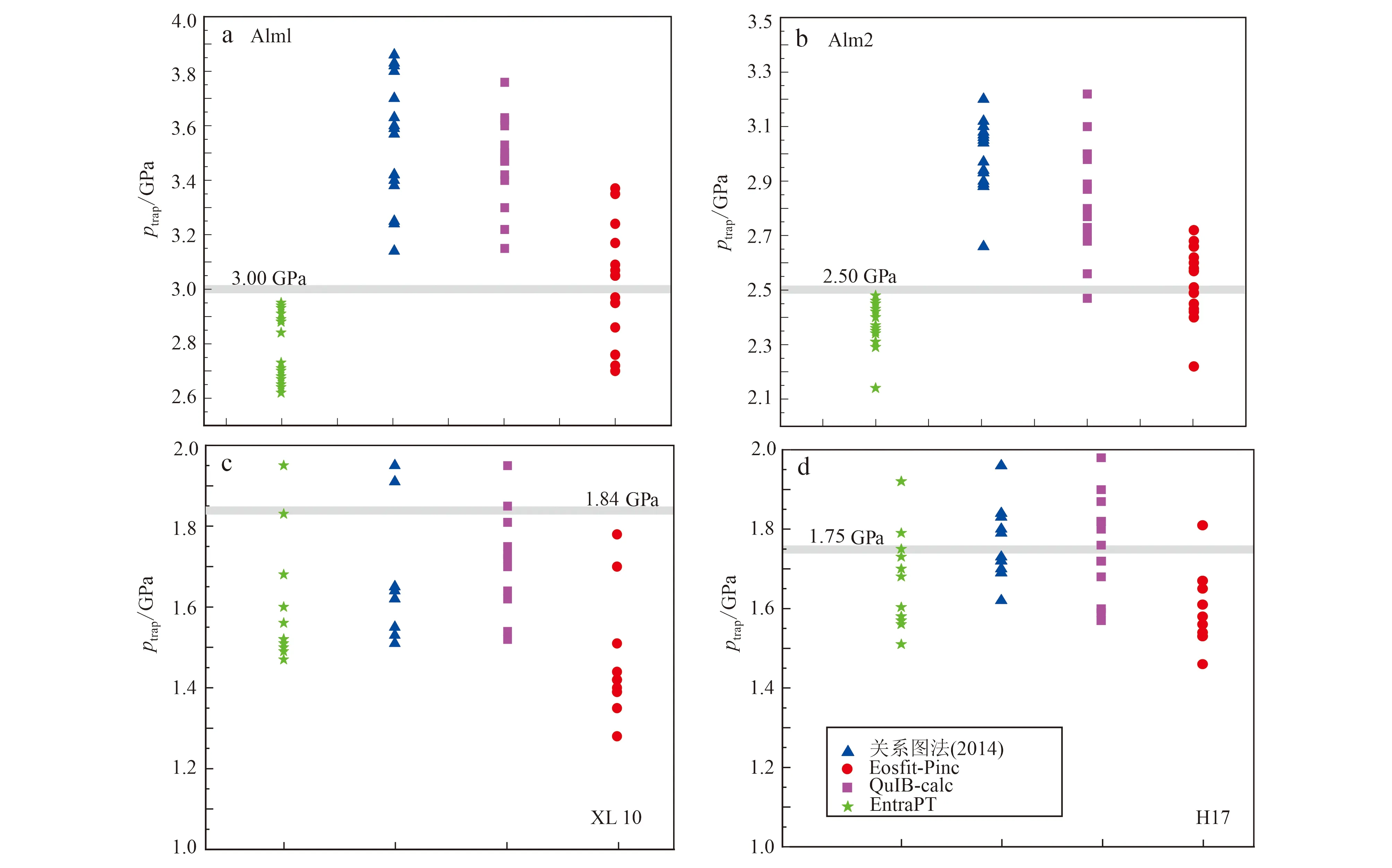
图 3 不同石英包体拉曼偏移压力计下石榴子石中石英包体的捕获压力Fig. 3 The entrapment pressure of quartz inclusions in garnet under different quartz Raman barometersAlm-1和Alm-2样品数据来自Bonazzi et al.(2019), XL10来自Zhang et al.(2022), H17来自本人的未发表数据; 灰色实线代表通过合成实验(Alm-1, Alm-2)与相平衡模拟(XL10, H17)获得的样品标准压力Alm-1 and Alm-2 are from Bonazzi et al. (2019), XL10 is from Zhang et al. (2022), H17 is from the author’s unpublished data; The solid gray line represents the sample standard pressure obtained by the syntheses experiment (Alm-1, Alm-2) and phase equilibrium modeling(XL10, H17)
相较于传统的热力学压力计,石英包体拉曼偏移压力计不受峰期变质组合保存状态的影响;对岩石地球化学成分特征依赖小;天然石英包体丰富,实验数据获取更加简单方便;针对不同的变质样品,选用合适的石英包体拉曼偏移压力计可获得与传统热力学压力计相吻合的结果。但是,这类压力计的应用是基于理想的两相矿物体系建立的,而天然的地质样品存在复杂性,如:天然矿物晶体都是弹性各向异性的,包体处于非静水压力场:高温-超高温条件会导致包体的弹性弛豫现象;寄主矿物的成分及包体矿物的大小和几何性质,这些都会对限定捕获压力产生影响。
4 结论
由于包体与寄主矿物具有不同的弹性性质,而且包体在折返过程会受到宿主矿物的限制,因此当温度压力发生变化时,它们会表现不同的体积变化,在包体内部形成残余压力。残余压力随着峰值变质压力的增加而增加,因此当其他指示物矿物缺失或被破坏时,包体的残余压力可以用来识别高压变质岩石以及恢复包体的捕获压力。本文介绍了一种利用石英包体拉曼位移进行变质条件约束的新方法。该方法考虑了矿物的压缩性和膨胀性对压力和温度的依赖,避免了由于弹性模型过于简化而可能造成的压力误差,可以较好地反映包体被捕获时的变质压力,是一个潜在的优质地质压力计。在利用石英包体拉曼偏移压力计时,要根据岩石特征选用合适的方法或程序,如Eosfit-Pinc更适用于高温下的压力测定,而EntraPT 程序和QuIB-calc则对于低温条件下复杂矿物成分体系的压力测定具有更高的准确度。随着实验技术的提高,这种物理与振动光谱学结合的方法将会应用到越来越多的天然样品中,具有广泛的应用前景。
