基于图卷积网络的柴油加氢生产软测量建模

冯子昊 梁 晨 谢忻南 唐 正 薛美盛

（中国科学技术大学信息科学技术学院自动化系）

柴油作为重要的石油产品，应用广泛。 近年来国家对柴油质量指标提出了更高的要求［1］。 为保障生产安全， 企业在提高生产效益的同时，需要严格把控产品质量，确保各个流程的指标符合国家标准。

精制柴油闪点（Flash Point，FP）和石脑油终馏点（Final Boiling Point，FBP）是柴油加氢生产最重要的质量指标，对保障生产安全具有重要的参考作用。 目前没有测量这两种指标的专用传感器或在线分析仪， 只能通过实验室化验法进行标定，而软测量是一种可行的替代方案。

软测量建模方法主要分为机理建模和数据驱动建模。 基于机理的软测量模型在内部反应机理明确的经典化工过程中广泛应用。 1978年，COLEMAN B B和MARTIN T对无法直接测量的质量指标设计了状态估计器［2］，首次提出了软测量的概念。 PRIYABRATA S和SANTOSH K G建立了丙烯聚合连续搅拌釜反应器的机理模型［3］，CHIC S等建立了聚乙烯反应过程的聚合产物成分软测量模型［4］，侯卫锋等研究了催化重整循环流程的机理建模［5］。

当过程变量严重耦合时，机理建模难以得到一个复杂系统的准确数学模型。 数据驱动建模是根据输入输出数据的变化规律建立软测量模型，不需要分析系统的反应机理。 因此，基于统计回归和经典前馈神经网络的建模方法逐渐取代了机理建模。 李春富等研究了使用偏最小二乘（Partial Least Square，PLS） 回归对间歇生产过程建立软测量模型的方法［6］。 CASEY K和STEVEN D B则融合随机森林（Random Forest，RF）建立了基于RF-PLS的脱丁烷塔软测量模型［7］。 黄锦等提出了基于支持向量回归的混合模型，预测了煤制乙炔浓度［8］。 LIU R L等基于模糊神经网络建立了系统过程参数、元素含量、气体浓度的软测量模型［9］。 VENKATA V S等提出了基于即时学习的广义回归网络软测量模型［10］。

随着深度学习的发展，深度神经网络大量应用在软测量建模中。 SHANG C等研究了基于深度神经网络的原油蒸馏装置重柴油95%点的软测量建模方法［11］。 WANG K C等基于卷积神经网络对互相关变量建立软测量模型［12］。 WANG Y L等基于注意力机制的动态堆叠自编码器网络建立了加氢裂化过程的软测量模型［13］。 YI L等基于集成深度学习对原油馏分产率进行软测量建模［14］。

柴油加氢生产过程较为复杂。 与闪点和终馏点关联的辅助变量多达数百种，过程变量存在非线性、强耦合等特点。 因此，机理模型和统计回归模型不能准确描述非线性系统内部的耦合关系。经典前馈神经网络的收敛速度慢，内部结构和训练机制简单， 不能实现有效信息的提取与聚合，影响软测量精度。 柴油加氢生产过程的质量指标数据都来源于实验室离线化验，数据采集时间长且数据规模小，使用深度网络建模容易出现过拟合现象，不能得到具有强泛化性的软测量模型。

针对上述问题，笔者采用机理分析法和数据可视化分析法选择辅助变量， 基于图卷积网络（Graph Convolution Network，GCN）［15］建立了精制柴油闪点和石脑油终馏点的软测量模型。 与传统前馈网络相比，图卷积网络收敛速度快，具有信息聚合能力和特征融合能力； 与深度网络相比，图卷积网络对小样本数据具有更强的泛化能力。

1 问题分析

1.1 柴油加氢生产系统概述

柴油加氢生产系统分为原料预处理系统、反应系统、高低分离系统、分馏系统、干气脱硫系统、辅助系统以及公用工程系统。 原料经过滤、缓冲、混合及换热等预处理操作进入反应器， 得到的反应产物经高压分离器进行气液两相分离， 分离的氢气进入脱硫塔实现循环利用。 低压分离器产出低分油之后送入汽提塔脱硫， 脱硫后的混合物输送至分馏塔进行分馏。 为确保产品的硫含量符合国家标准GB/T 19147—2016《车用柴油》的要求，分馏后的产品要经过干气脱硫系统再次脱硫。

柴油加氢生产工艺要求精制柴油闭口闪点不低于62 ℃，加氢石脑油终馏点不超过184 ℃。根据精馏原理， 柴油和石脑油的馏程存在明显差距，可以通过分馏实现产品分离。 作为分馏塔进料的重组分，精制柴油自塔底收集，经多个换热器和塔底空冷器送至精柴出装置。 塔顶油气包含石脑油，经塔顶空冷器冷却后进入冷回流罐。

1.2 质量指标软测量难点

柴油的闪点是指柴油在加热时，溢出蒸气与空气的混合物质在接触火焰时发生瞬间闪火所需的最低温度。 柴油混入的轻组分越多，沸点越低，馏程越低，蒸气压越高，越容易达到柴油爆炸下限。 因此，柴油的闪点越低，越易燃，其数值取决于柴油的馏程［16］。

石脑油是汽油粗制产品， 不同的分离产物对应石脑油不同的馏程。根据生产需求，选择具有相应终馏点的石脑油作为原料， 如果石脑油的质量指标不符合要求，就无法保证最终产品的质量［16］。

目前没有可以在线测量闪点和终馏点的仪器，只能通过实验室离线化验得到准确数值。 实验室分析一次柴油闪点需要约40 min， 完成一次分析之后必须等待仪器降温至所需温度才能进行下一次分析实验［17］。这会影响产品的调整周期，降低生产效率和产品质量，生产安全也不能得到保证。 因此，软测量是解决闪点和终馏点在线估计的可行替代方案。 柴油加氢生产系统涉及多个连续反应单元， 机理分析难以建立精确的数学模型。 闪点和终馏点在一定程度上存在耦合，相关过程变量多， 统计回归模型难以准确描述强耦合、非线性变量之间的关系。 传统前馈网络不能充分学习变量之间的关联信息，模型的收敛速度慢，影响软测量的准确性和快速性。 柴油加氢生产过程的质量指标化验时间长、 数据规模小，仅少量样本可以用于软测量建模，使用深度网络建立的软测量模型泛化能力差，过拟合风险高。

2 辅助变量的选择

辅助变量的选择和数据的质量影响软测量模型的精度。 辅助变量过多会增加模型的复杂度，降低运算效率；辅助变量过少会因信息缺失出现模型欠拟合现象，降低模型的准确性。 柴油加氢生产过程涉及的状态变量多达约260种，需要对辅助变量进行选择。

辅助变量的选择方法主要分为机理分析法和数据分析法。 只通过机理分析选择变量容易因经验和知识的缺乏忽略隐含的强相关变量，只通过数据特征选择变量可能忽略具有重要物理意义的变量。 因此，结合机理分析和数据分析选择变量能够提高输入信息的完备性，避免无关变量干扰主导变量的预测。

为选择关键变量，笔者首先分析了柴油加氢生产过程的机理，明确了变量的物理意义和影响因素。 其次，笔者对过程数据进行可视化，分析了辅助变量的分布特征和相关性，得到了机理分析无法确定的强相关变量。

2.1 工艺机理分析

在分馏系统中， 分馏塔进料的沸点随塔内温度和压力动态变化。 根据Clausius-Clapeyron方程［16］，某一单组分系统达到相平衡时，压强p随温度T的变化关系为：

恩氏蒸馏原理［16］表明，通过测量油品在加热过程中不同时刻的恩氏蒸馏温度可以得到准确的闪点和终馏点。 所以，温度和压力是影响闪点和终馏点的关键变量。 笔者结合柴油加氢生产过程机理分析辅助变量的直接影响因素，分析结果见表1。

表1 辅助变量的直接影响因素

精制柴油作为重组分从分馏塔塔底进行收集，塔底温度和液位会影响柴油的闪点。 重组分一部分来源于塔顶回流液的二次蒸馏，塔顶回流罐的状态变量也会影响柴油闪点，如塔顶回流罐压力、液位及流量等。 石脑油作为轻组分自塔顶收集，分馏塔的进料温度、塔顶温度、塔顶回流量及塔顶回流罐压力等变量都会影响石脑油的终馏点。

柴油加氢生产过程总是将两种或两种以上的变量保持一定比例关系，比例一旦失调，会直接影响生产甚至造成事故。 为提高模型输入信息的完备性， 笔者重构了8组基于实际变量比例关系的辅助变量，见表2。 例如，塔顶回流量和回流罐压力都影响闪点和终馏点，而塔顶回流量和回流罐压力存在关联关系。 因此，用回流罐压力和塔顶回流量的比值作为新的特征来衡量回流罐内的气液相平衡关系。

表2 辅助变量重构结果

2.2 辅助变量特征分析与数据可视化

箱型图是一种数据统计分布的可视化方法。箱长、 箱顶和箱底分别表示样本的四分位距、75%分位数和25%分位数，箱内分界线表示样本的中位数。从箱内分界线的位置可以判断样本的偏态程度，超出箱型图边缘的样本数据视为离群点。 经归一化的辅助变量箱型图如图1所示，存在较多离群值的辅助变量集为{A，H，J，L，O，P，Q，U，W}， 呈偏态分布的辅助变量集为{B，C，F，H，M，O，V}。

图1 归一化的辅助变量箱型图

方差过滤是一种特征选择方法。 辅助变量的方差可以反映数据波动情况和特征的信息量，低方差变量容易使模型学习到近似噪声的分布规律，降低模型精度。 笔者通过方差过滤保留了具有高方差的辅助变量，剔除了低方差特征。 如图2所示，辅助变量集{F，P，S，U}的方差均小于0.01，不能作为模型的输入。

图2 辅助变量方差分布

为分析辅助变量的统计分布， 需要对变量进 行 核 密 度 估 计 （Kernel Density Estimation，KDE）。 通过变量的分布直方图绘制KDE曲线，如图3、4所示，变量T的分布近似正态，变量H的分布则是偏态的。 根据变量的KDE可视化结果，变量集{A，D，E，G，J，L，N，R，T，W}呈正态分布，变量集{B，I，K，M，V}则出现偏态。 偏态分布使数据的样本均值和样本方差不独立， 干扰模型学习。 因此，在模型输入前，需要对呈偏态分布的数据正态化处理。

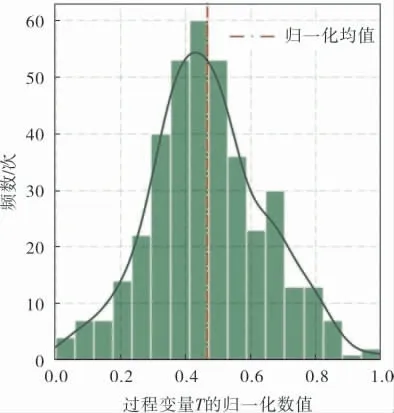
图3 变量T的KDE曲线

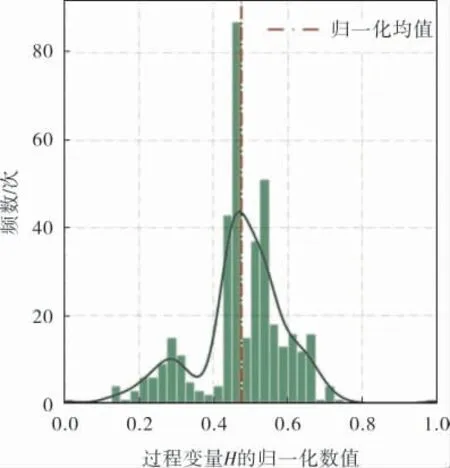
图4 变量H的KDE曲线

图5是基于Spearman系数的辅助变量相关性分布图， 以每个元素的热度表征了变量之间的Spearman相关性， 即相关系数。 矩阵元素的颜色越深， 则其对应的两个变量的正相关性越强；反之，负相关性越强。

图5 辅助变量的Spearman相关性分布图

2.3 辅助变量的选择结果

通过机理分析方法得到的辅助变量选择结果见表3。

表3 基于机理分析的辅助变量选择结果

通过特征分析方法得到的辅助变量选择结果见表4。

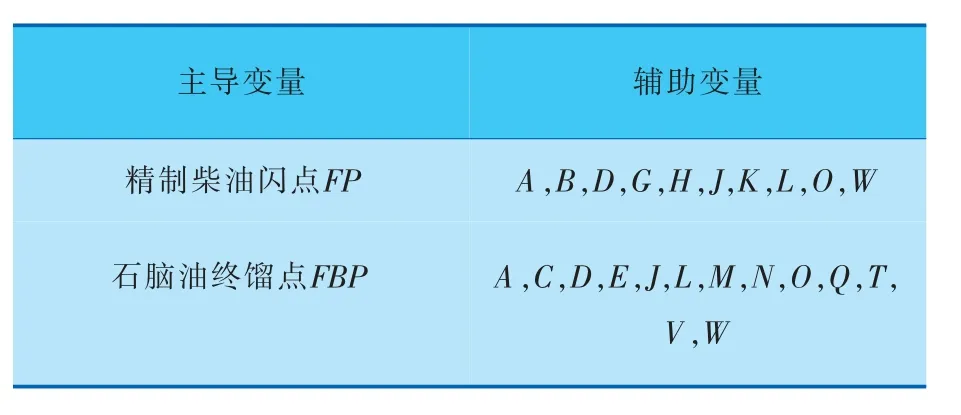
表4 基于特征分析的辅助变量选择结果

由于重构变量仅从机理角度考虑，可能存在不显著、低相关等问题。 因此，重构变量选择更侧重于数据特征分析的结果， 选择具有高方差、高相关、高信息量的重构变量作为软测量的辅助变量，如变量O和W。 基于机理分析和特征分析，精制柴油闪点和石脑油终馏点的变量选择结果见表5。

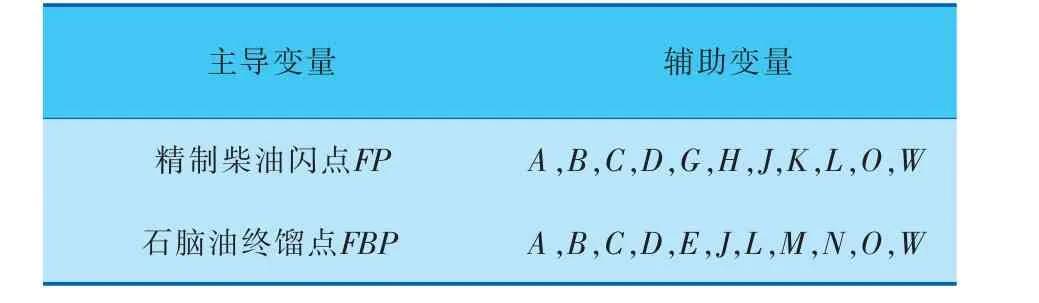
表5 柴油加氢生产过程软测量模型的辅助变量与主导变量

3 基于图卷积网络的软测量模型

在经典前馈神经网络的基础上，图卷积网络实现了信息聚合和特征融合，对小样本数据建模具有更强的鲁棒性。 笔者基于谱域GCN建立了软测量模型， 以处理后的变量作为模型的输入，以精制柴油闪点和石脑油终馏点的预测值作为模型的输出。

谱域GCN以无向图作为训练数据在神经元中传递，训练过程包括特征融合、信息更新和循环优化。 如图6所示，GCN的整体架构依然是由输入层、隐含层和输出层组成的，其中隐含层具有多个图卷积层。 仅通过无向图中结点的单一特征不能使模型充分推理该结点的类别，需要融合邻接结点的特征， 增强各个结点特征的表征能力。经一次聚合，结点融合了一阶邻接点的特征。 为得到更完备的特征信息，再经二次聚合，结点通过一阶邻接点已聚合的特征，间接融合了二阶邻接点的特征，循环迭代。 最后对每个结点的输出特征进行分类或回归， 计算损失并优化网络权值。 因此，每个图卷积层都是对输入数据进行特征扩散与聚合操作。

图6 图卷积网络的信息聚合机制

GCN对各个结点的度进行对称归一化，融合了自身结点的特征形成闭环，避免其他邻接点淹没了当前结点的特征信息。 若无向图具有n个结点，则GCN的特征传递机制表示为：

GCN的神经元传递了具有非欧氏结构的图表征数据，无向图中结点间的拓扑关系和连接强度是基于其邻接矩阵A-建立的数学描述， 连接强度量化了结点之间的信息梯度。 然而，在实际工业过程中，传感器采集的过程变量集合构成的是一种欧氏数据， 无法直接用邻接矩阵显式计算。因此，用基于过程变量的互信息量来表达其构成的无向图之间的连接关系是一种可行方案。

其中，EN（·）表示变量的Shannon熵；EN（·，·）表示两个变量之间的联合Shannon熵。

如果网格数是固定的， 则不同的网格划分方法能够得到不同的MI（DS｜G）。 基于最大互信息量计算最大互信息系数MIC（DS），并以此确定由过程变量所构成结点的初始特征， 代替了邻接矩阵A-，即：

4 仿真研究

4.1 数据预处理与特征提取

为消除数据量纲和数据偏态性对模型精度的影响，需要在输入前对数据进行归一化和规范化，即：

其中，Cov（u，v）表示随机变量u和v的协方差，σu和σv表示其对应的标准差。

经计算柴油加氢过程数据集辅助变量的Pearson相关系数矩阵，可以发现辅助变量之间存在多重共线性。 为避免多重共线性对模型精度的影响，需要对辅助变量进行特征提取。 笔者基于主元分析法减小了辅助变量之间的多重共线性，得到了低维且稠密的特征变量，以此作为软测量模型的输入。 主元分析法基于样本的协方差矩阵衡量特征的相关性，基于样本方差衡量特征的信息量。 为度量降维特征的信息量，笔者以累计方差贡献率（Cumulative Varian ce Contribution Rate，CVCR）作为主元个数选择的依据，即：

在模型计算量允许的前提下， 尽可能选择CVCR高的主元个数。 当CVCR＞0.95时，降维特征包含了原始特征的主要信息。 如图7、8所示，当两个辅助变量集的主元个数为8时，CVCR均达到0.95以上。 因此，笔者以8个主元的降维特征作为软测量模型的输入。

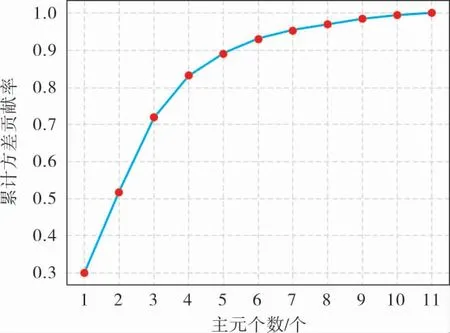
图7 精制柴油闪点的累计方差贡献率

图8 石脑油终馏点的累计方差贡献率

4.2 软测量建模仿真

本课题的软测量实验仿真数据来自某石化公司的柴油加氢生产过程。 数据经预处理和特征提取后，按照8∶1的比例划分为训练集和测试集，以软测量模型的预测结果ye与真实化验值y之间的均方误差（Mean Square Error，MSE）作为网络训练的损失值loss， 采用均方根误差 （Root Mean Square Error，RMSE）和最大绝对误差（Maximum Absolute Error，MAE）作为模型精度的评价指标，即：）

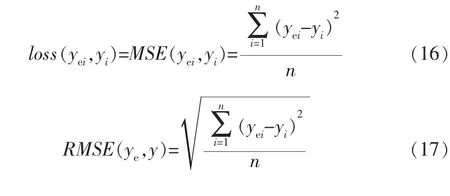
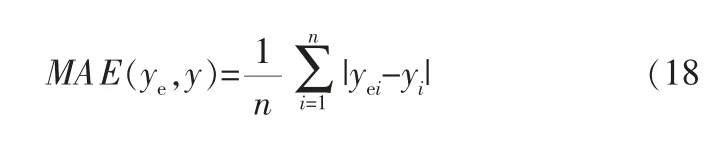
其中，yei表示在第i个采样时刻质量指标的预测值，yi表示在第i个采样时刻质量指标的离线化验值，n表示样本数量。

笔者使用最大互信息系数矩阵代替邻接矩阵作为GCN的训练数据，建立了基于GCN的软测量模型。 网络结构及其维度如下：

输入层 8

隐含层 1×3

隐含层 3×1

全连接层 8×1

网络配置参数如下：

迭代次数 2 000

学习率 0.01

损失函数 MSE

优化器 Adam

图9、10分别是精制柴油闪点和石脑油终馏点的真实值和软测量模型输出的预测值， 模型输出的预测值稳定在±5%的置信区间内， 并标注了闪点和终馏点的参考控制限（分别为62 ℃和184 ℃）。 基于GCN的软测量模型精度的计算结果见表6。

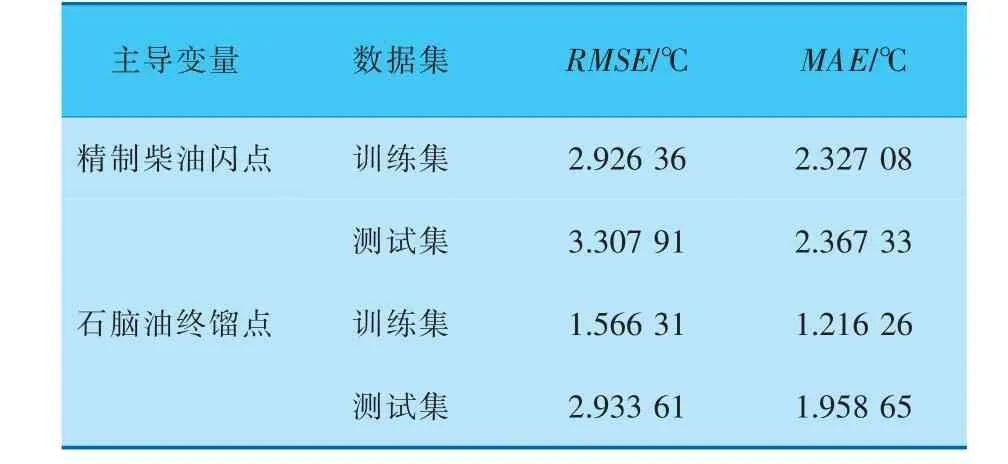
表6 图卷积网络软测量模型的精度评价指标

图9 基于GCN的精制柴油闪点软测量建模结果

图10 基于GCN的石脑油终馏点软测量建模结果

4.3 模型精度对比

为验证并比较基于GCN的软测量建模效果，笔者选择目前广泛应用的6种软测量模型进行仿真对比研究， 包括偏最小二乘 （Partial Least Squares，PLS）、 支 持 向 量 回 归 （Support Vector Regression，SVR）、 多 层 感 知 机 （Multilayer Perceptron，MLP）、 径 向 基 网 络 （Radial Basis Network，RBF）、循 环神经网 络（Recurrent Neural Network，RNN）和门控循环单元（Gated Recurrent Unit，GRU）。 基于精制柴油闪点和石脑油终馏点建立上述7组软测量模型之后， 计算各组模型的软测量精度，得到的对比实验结果见表7、8。

表7 精制柴油闪点软测量模型精度对比

表8 石脑油终馏点软测量模型精度对比

对比结果表明，相比于统计推理算法（如PLS和SVR）、前馈网络模型（如MLP和RBF）和循环网络模型（如RNN和GRU），基于GCN的软测量模型在精制柴油闪点和石脑油终馏点两个质量指标上都具有更小的RMSE， 说明了GCN在软测量建模中的有效性，并且GCN的信息聚合机制使软测量模型具有更高的平均精度，在两个不同的质量指标上都具有良好的表现。 MAE小， 说明基于GCN的软测量模型相比于其他6种模型而言，产生的最大误差更小，具有较好的鲁棒性，可以自适应地跟踪外部输入的剧烈变化。 因此，GCN有效地提升了精制柴油闪点和石脑油终馏点的软测量准确性和鲁棒性，具有更好的泛化能力。

5 结束语

笔者提出了基于图卷积网络的柴油加氢生产软测量方法，解决了精制柴油闪点和石脑油终馏点的在线测量问题。 首先从工艺机理的角度分析了辅助变量的物理意义和机理关系，从数据特征的角度分析了辅助变量的统计分布和相关性，完成了辅助变量的筛选和重构。 然后对图卷积网络软测量模型进行了仿真研究。 结果表明，相比于传统前馈神经网络和循环神经网络，基于图卷积网络的软测量模型具有更高的测量精度和更快的收敛速度，在实际应用中具有可行性、准确性和高效性。