基于鲸鱼算法优化深度极限学习机的锂离子电池剩余使用寿命间接预测
2023-02-13王海瑞朱贵富
郝 锐 王海瑞 朱贵富
(昆明理工大学信息工程与自动化学院)
锂离子电池是一种绿色高能充电电池,凭借能量密度大、自放电率小及无污染等优势[1]被广泛应用,如电动汽车、电子产品(手机、笔记本电脑)等领域。 随着锂离子电池应用的日益普及,其剩余使用寿命(Remaining Useful Life,RUL)预测也愈发重要。 在实际使用过程中,锂离子电池会随着循环充放电次数的增多、外部复杂工况及自身结构变化等因素,产生容量减少和内阻增大的现象,导致其性能逐渐退化,进而影响电池的正常可靠运行[2]。因此,对电池的RUL进行准确预测具有重要意义。
锂离子电池寿命预测方法主要分为两类:基于模型的方法和基于数据驱动的方法[3]。 基于模型的方法是通过一系列代数和微分方程的数学方法构建描述锂离子电池老化行为的模型,以此对电池RUL进行预测,如等效电路模型[4]、经验模型[5]等。 基于数据驱动的方法不需要分析电池内部的物理、化学反应过程,直接利用锂离子电池容量的历史数据来构建预测模型[6],主要方法有ANN、SVM、RVM等。 电池RUL预测的核心就是预测电池容量衰减到失效阈值时剩余的循环次数。然而,在实际应用中,由于诸多因素导致电池容量不易直接测量,若直接利用电池历史容量进行寿命预测,会因为历史数据有限而导致模型预测效果不明显,所以这种方法实用性不强。 因此,从恒流充放电过程中测得的电流、电压等参数中提取间接健康因子的间接预测方法被逐渐采用。 目前,利用健康因子(HI)进行间接预测的方法解决了直接参数不易测量的问题,更具实用性,如使用 等 压 降 时 间 间 隔[7]、电 池 端 电 压[8]等 参 数 单 独作为HI进行电池RUL预测,文献[9]选择等压降放电时间作为间接健康因子,构建基于ELM的间接RUL预测模型。 但是由于ELM算法的权值和阈值是随机生成的,没有对它进行优化,严重影响了预测效果。
本研究从恒流放电过程中提取出间接健康因子,分析其与电池容量之间的相关程度,并将其作为模型的输入,容量作为模型输出。 此外,提出采用鲸鱼优化算法优化深度极限学习机模型参数,构建WOA-DELM预测模型,通过锂离子电池数据集中的两个电池对该模型预测进行分析与验证。 最后与BP神经网络、 深度极限学习机(DELM)、PSO-DELM方法进行对比分析, 证实构建的WOA-DELM模型在锂离子电池RUL预测方面的优势。
1 算法原理概述
1.1 深度极限学习机
自动编码器(AE)经过训练可以将输入X复制到输出Y,并且训练过程是不受监督的[10]。 因此,将极限学习机(ELM)与AE相结合,引入AE的思想应用到ELM中, 同样将ELM的输入数据复制到输出,即Y=X,以此构建极限学习机-自动编码器(ELM-AE),网络结构如图1所示。

图1 ELM-AE网络结构示意图
当s>L,ELM-AE实现维度压缩; 当s=L,ELMAE实现等维度特征表达; 当s<L,ELM-AE实现原始数据的高维特征表达[11]。
将ELM-AE作为无监督学习的DELM基本单元对输入数据进行训练与学习。 DELM的特点是不需要进行微调,速度快。
因为在ELM-AE网络中输出等于输入,那么隐含层特征H的输出权值矩阵为:

其中,I为单位矩阵;λ为正则化系数。
每层输出的特征的计算式为:

其中,Hi表示第i层ELM-AE的输出;Hi-1为第i-1层ELM-AE的输出;g为隐含层的激励函数;β为输出权值。
学习到的特征Hi随隐含层层数的增加而呈递减趋势。 DELM结构如图2所示。

图2 DELM结构示意图
1.2 鲸鱼优化算法
鲸鱼优化算法(WOA)是一种新型启发式优化算法,模拟自然界中座头鲸的狩猎行为进行运算,其优点是操作简单、调整参数少和跳出局部最优的能力强[12]。
WOA算法分为3个步骤。
第1步 包围猎物。 为了描述鲸鱼的狩猎行为,用如下数学模型来表示:
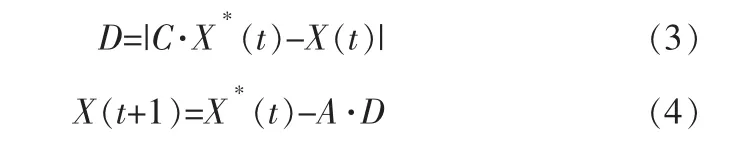
其中,D表示当前鲸鱼最优个体位置与其他鲸鱼个体位置之间的距离;A和C都是系数,A=2αR1-α,C=2R2,α=2-2t/TMax, 随 机 数R1、R2∈[0,1],α的值从2到0呈线性下降,TMax为最大迭代次数;t为当前迭代次数;X*为目前得到的最佳位置向量。
第2步 狩猎行为。 座头鲸采用收缩包围和螺旋运动同步发生的方式游向猎物进行狩猎。 假设选择收缩包围机制和选择螺旋模型来更新鲸鱼位置的概率都相等,均设置为0.5。 则狩猎行为的计算式为:
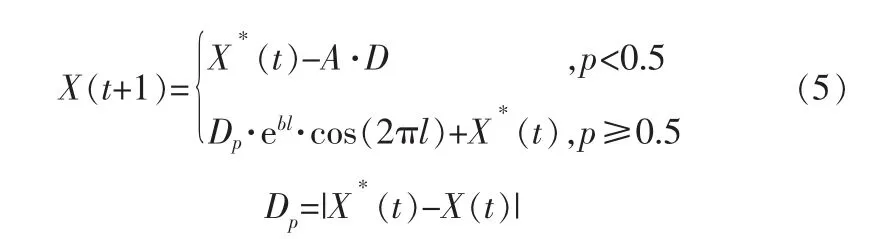
其中,Dp表示鲸鱼和猎物之间的距离;b为常数,它决定了对数螺线的形状;随机数l∈[-1,1];随机数p∈[0,1]。
第3步 搜索猎物。 该阶段与狩猎行为不同,座头鲸会随机搜索猎物。 根据随机选择的鲸鱼位置来更新其他鲸鱼的位置,以此找到一个更合适的猎物,这样可以加强算法的搜索能力,使WOA算法能够进行全局搜索[13]。 基于可变向量A,当|A|<1时属于包围捕食阶段,通过式(4)更新目前搜索代理的位置,因为在狩猎行为中的收缩包围机制在本质上也属于包围捕食阶段; 当|A|≥1时选择一个随机搜索代理Xrand通过式(7)更新目前搜索代理的位置,数学模型如下:
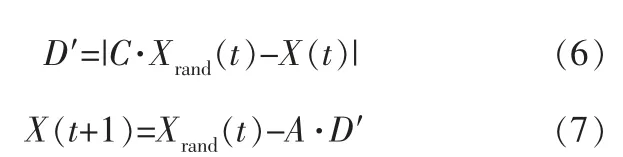
其中,Xrand表示随机选择的鲸鱼位置向量;D′表示随机鲸鱼与参考鲸鱼之间的距离。
1.3 WOA-DELM方法
DELM网络精度受各ELM-AE随机输入权重与随机偏置的影响,为此,本研究采用WOA进行这些参数的寻优,以提高DELM的预测精度。 基于WOA-DELM的锂离子电池RUL预测流程如图3所示。
基于WOA-DELM的锂离子电池RUL预测的主要步骤如下:
a. 提取健康因子和数据预处理,从电池数据集中提取间接健康因子并进行数据归一化处理。
b. WOA-DELM 模型参数设置, 种群数量popsize为30,最大迭代次数Max_iter为100,权值下边界lb为-1, 权值上边界ub为1;DELM参数,ELM-AE的激活函数ActivF为‘sig’,正则化系数λ为inf。

d.WOA优化DELM网络参数, 将鲸鱼优化算法获得的最优参数给DELM进行训练并预测,构建WOA-DELM预测模型。
e. 电池RUL预测,将测试数据、输出权值及ELM-AE隐含层数等输入网络进行预测, 实现电池RUL的预测并验证方法的可行性。
2 锂离子电池间接健康因子的构建
2.1 实验数据集
实验所用数据集来源于NASA艾姆斯研究中心。 电池是型号为18650的市售锂离子电池,额定容量2 A·h,额定电压4.2 V[14]。 该数据集有4个型号相同的锂离子电池 (B0005、B0006、B0007和B0018),在充电、放电和阻抗3种测试工况以及室温24 ℃条件下测得。 此外,规定寿命预测的失效阈值为1.4 A·h(即电池额定容量减少30%)。
观察图4所示的各电池容量的衰减曲线可以发现,B0007号电池在整个寿命循环周期中电池容量并没有降至失效阈值,为了方便实验对比分析,将失效阈值设置为1.44 A·h。

图4 各电池容量衰减趋势
由图4可知,随着放电循环次数的增加,电池容量总体呈退化趋势。 但是,局部会出现容量再生现象, 即在电池充放电结束后会短期搁置,在这个时间段内电池内部电极附近生成的减缓电池内部反应的聚集反应物会消散,使得下一充放电周期的容量会出现局部短暂增加的现象。
2.2 间接健康因子的提取
由于锂离子电池的直接参数(容量、内阻)难以直接测量, 在实际应用中存在很大的局限性。因此,本研究从可监测的间接参数着手,选择从恒流放电过程中提取等压降放电时间作为HI。 将锂离子电池每个恒流放电周期中电压从高电压放电至低电压所经历的时间称为等压降放电时间[15],其计算式为:


2.3 评估特征参数相关性
选择相关系数来分析两个变量之间的相关性R,其计算式如下:

当R属于0.8~1.0之间时,为极强相关;当R属于0.6~0.8之间时,为强相关;当R属于0.4~0.6之间时,为中度相关;当R属于0.2~0.4之间时,为弱相关;当R属于0.0~0.2之间时,为极弱相关;当R为0.0时,为不相关。
一阶偏相关系数就是在控制一个变量的情况下, 研究分析两个变量之间关系的一种方法。由图4、5可以看出, 锂电池的电池容量和等压降放电时间序列都与循环次数相关,所以在控制电池循环次数不变的条件下,利用一阶偏相关系数来分析等压降放电时间ΔT和电池实际容量Q之间的相关性[16]。 RΔTQ,c表示ΔT和Q之间的相关系数,其计算式为:
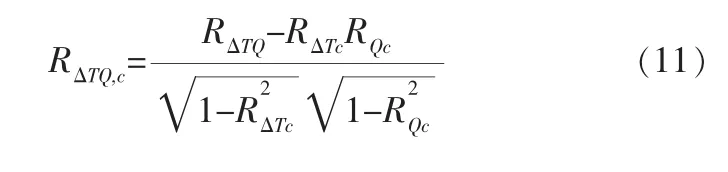
其中,RΔTQ表示电池实际容量Q与等压降放电时间ΔT的相关系数;RΔTc表示循环次数c与等压降放电时间ΔT的相关系数;RQc表示电池实际容量Q与循环次数c的相关系数。
3 实验验证与分析
本研究通过一阶偏相关系数分析方法计算出R=0.8524(R∈(0.8,1.0]),属于极强相关,验证了所提方法的可行性。 利用B0005、B0007号电池对所提预测方法进行验证与分析, 并且和其他3种预测方法进行对比分析。 各种方法的参数信息见表1。

表1 各预测方法的参数设置
B0005、B0007号电池预测结果如图6、7所示。
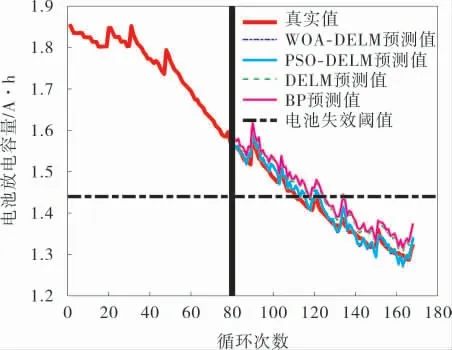
图6 B0005号电池在4种方法下的预测结果
为了能够更直观地查看各种方法的预测精度,实验中引入平均绝对误差(MAE)和均方根误差(RMSE)对实验结果进行评价分析,定义如下:
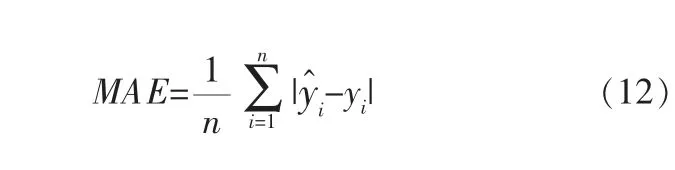

图7 B0007号电池在4种方法下的预测结果

其中,y^i表示第i次预测的预测值;yi表示第i次预测的真实值。
本实验采用B0005、B0007号电池分别在4种预测方法下测得各电池的预测数据见表2。
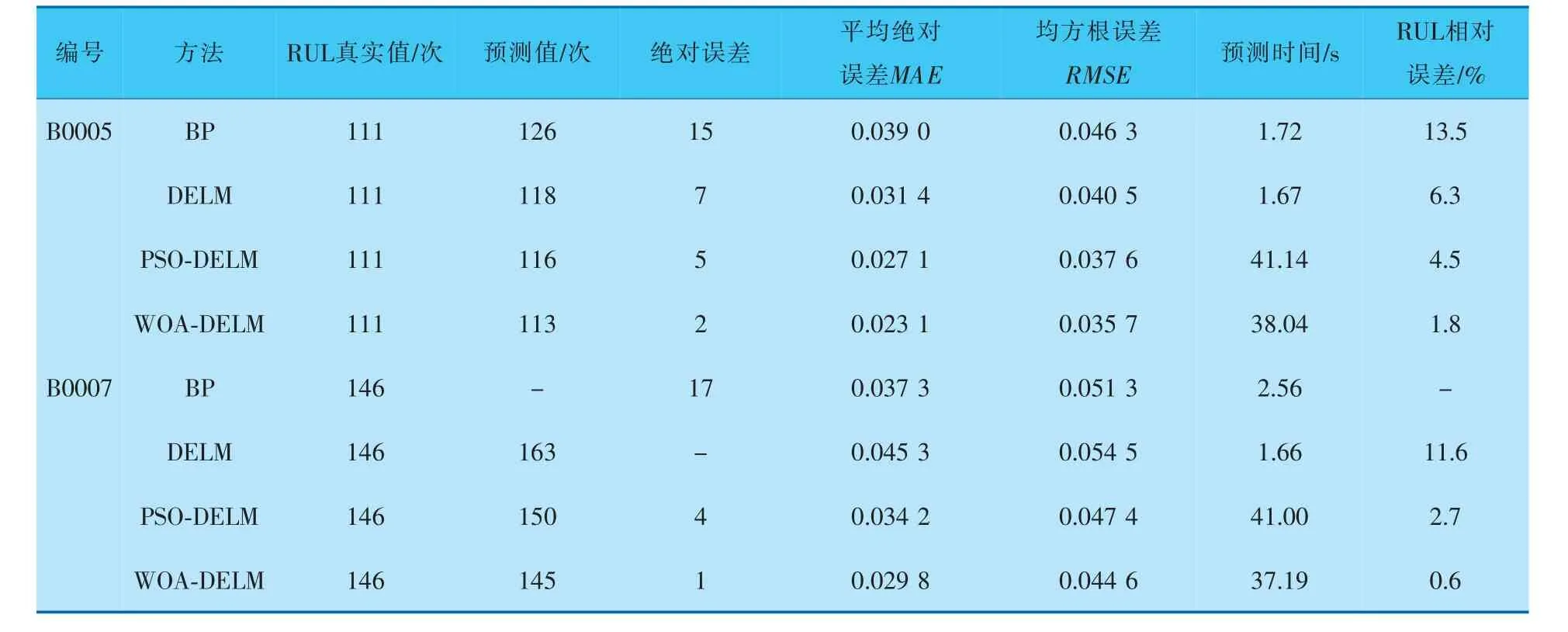
表2 4种方法的RUL预测结果性能分析
由表2可知, 对于不同编号的电池,WOADELM相比于BP、DELM、PSO-DELM方法, 其预测得到的MAE、RMSE、 绝对误差都比较小,说明其预测精度更高。 例如,在B0005、B0007号电池中,BP方法预测的绝对误差最大分别为15和17,WOA-DELM 方法预测的绝对误差最小,分别为2和1。
此外, 用不同算法优化DELM网络预测的误差和所花费的时间也不同。 在保证两种算法参数设置相同的情况下,这里用PSO优化DELM对比分析WOA优化DELM,从表2中可以看出,以B0005号电池为例,WOA-DELM预测的MAE、RMSE值分别 为0.023 1 和0.035 7,PSO-DELM 预 测 的MAE、RMSE值分别为0.027 1和0.037 6, 所花费的预测时间分别为38.04 s和41.14 s,表明WOA-DELM预测效果更佳。
从表2可以看出, 在B0005号电池中,BP方法测得的绝对误差、RUL 相对误差分别为15 和13.5%,DELM方法测得的绝对误差、RUL相对误差分别为7和6.3%,PSO-DELM方法测得的绝对误差、RUL相对误差分别为5和4.5%,WOA-DELM方法测得的绝对误差、RUL相对误差分别为2和1.8%。B0007号电池也类似,但特殊的是B0007号电池在DELM方法测试时预测值一直没有达到失效阈值。
从图6、7的预测结果和表2的预测数据中可以看出, 在两个不同电池数据下,WOA-DELM预测结果的绝对误差、RUL相对误差、平均绝对误差MAE、 均方根误差RMSE分别是各个对比实验组中最小的, 其预测误差范围都在±5%以内, 表明WOA-DELM预测效果明显优于其他3种方法。
4 结束语
通过研究NASA锂离子电池数据集, 从恒流放电过程中提取出间接健康因子,分析其与电池容量之间的相关程度;提出WOA优化算法,针对DELM网络存在的缺点为其寻找出最优参数,从而构建基于WOA-DELM的预测模型, 实现电池RUL的间接预测。 此外, 还利用BP神经网络、DELM和PSO-DELM方法进行预测结果对比分析,验证了所提方法的可行性。
