基于前馈补偿的永磁直驱电机低速抗扰动滑模控制策略
2023-02-13李晨曦卜飞飞秦海鸿
刘 佳,李晨曦,李 荣,季 飚,卜飞飞,秦海鸿
(1.南京航空航天大学自动化学院,南京 211106; 2.中国船舶重工集团公司第七二四研究所,南京 211106; 3.上海机电工程研究所,上海 201100)
0 引 言
传统伺服系统利用齿轮、齿条等零件作为传动机构来连接各部件,但齿轮、齿条之间存在齿隙公差,会造成传动系统精度低、易磨损、维护不方便等诸多问题[1],在精度和可靠性要求高的情况下可能达不到使用要求。与之相对,永磁直驱伺服电机由于取消了减速机等中间机构,直接连接负载,在控制精度和可靠性等方面远超于传统传动机构,在航空航天、数控机床等高精度控制场合有着更广阔的应用前景[2]。由于没有减速器等中间环节,齿槽效应、负载变化、高次电流谐波、机械摩擦等多种干扰,会直接作用在电机轴上,影响调速系统的运行精度和稳定性。如何提升系统的抗干扰能力,是永磁直驱伺服系统在实际应用中面临的关键问题之一。
在高精度电机控制领域,常规的PID控制会受到系统参数变化的影响,在非线性时变系统中表现欠佳,可能会造成放大器饱和即微分作用环节效果减弱等结果,在扰动等非线性因素影响较大的情况不适合使用或者单独使用这种控制方案[3]。针对电机负载扰动问题,国内外研究人员提出了比例谐振控制[4]、重复控制[5]、自抗扰控制[6]、模糊控制[7]、滑模控制[8]等扰动抑制方法。其中,比例谐振控制与重复控制需要具体的扰动信息,应用起来相对局限;未知转矩扰动的抑制方法,比如模糊控制、自抗扰控制,算法设计较为复杂。而滑模控制不依赖系统的数学模型,同时对于扰动及不确定因素的变化不敏感,算法相对其它扰动抑制算法结构较简单,易于实现,在工程应用中具有明显的优势[9-13]。
文献[14]利用分数阶微积分设计了一种分数阶滑模控制器,提高了永磁同步电动机非线性速度控制的鲁棒性,但分数阶滑模控制器的设计较为复杂。文献[15]提出了一种扩展滑模扰动观测器来估计和补偿扰动,可以达到较高的控制精度,但扩展观测器参数较多。文献[16]采用积分型的滑模结构,并同时添加了对转矩估计的龙伯格全维状态观测器环节,可以更有效地削弱扰动影响且使系统无稳态误差。但是全维观测器结构设计复杂,存在依赖系统状态参数的缺点[17-20]。
使用改进滑模控制器与观测器前馈补偿两种方法的组合是一种解决永磁直驱伺服系统扰动的良好方案,一方面提升了系统的扰动抑制能力,另一方面降低了控制系统对电机参数的依赖程度,同时降阶观测器的引入能够有效简化观测器的参数设计过程[21-22]。
基于上述背景,本文针对永磁直驱伺服电机运行时负载扰动的影响,研究了基于前馈补偿的永磁直驱伺服电机抗扰动滑模控制策略,通过优化指数趋近率设计,调整了不同趋近状态下滑模系统的趋近速度,以降低系统高频抖振问题;同时引入降阶状态观测器对系统进行扰动观测及补偿,较全维状态观测器设计简单,提升了系统的扰动抑制能力。仿真及实验证明,这种复合控制策略可以有效地减小抖振的影响,提高速度控制的鲁棒性。
1 永磁电机数学模型
本文的永磁直驱伺服电机为表贴式永磁同步电机。假设气隙磁动势正弦分布,不计电机涡流以及磁滞损耗,忽略电机电枢反应,采用id=0控制策略对系统进行解耦控制,电机励磁全部通过永磁体产生[23]。永磁同步电机电压方程:
(1)
转矩方程:
(2)
机械运动方程:
(3)
式中:ω为机械角速度;p为极对数;ud和uq为d和q轴的电枢电压分量;id和iq为电枢电流分量;Rs为电枢电阻;ψf为电机转子磁链;Lq为电机交直轴电感;Te为电磁转矩;J为转动惯量;TL为负载转矩;Ba为阻尼系数。
从式(3)可以看出,电机机械运动方程包含转矩及速度变化值,永磁直驱伺服电机极对数较多,电机额定转速较低。由于没有中间传动机构,扰动转矩如齿槽转矩、负载转矩直接作用在传动轴上,对于速度控制的平稳性会产生较大影响。以齿槽转矩为例,转速变化值近似等于转矩除以电机惯量对时间的积分,低速时速度波动会更加明显。因此,提升电机的扰动抑制能力对永磁直驱伺服系统具有重要意义[24]。
2 基于改进趋近率的滑模控制器设计
滑模速度控制器是对非线性不确定系统的一种有效的控制方法,具有其结构简单、鲁棒性强、对扰动参数影响不敏感、响应速度快等诸多优点,在电机抗扰动领域已经有诸多应用[25]。基于改进趋近率的滑模控制器构建过程中,需要设计系统滑模面及趋近率,来迫使系统按照预定“滑动模态”的状态轨迹运动。
2.1 微分型滑模面设计
本文采用传统的微分型滑模面,在指数型趋近率基础上,引入新型趋近率函数,以提高系统的抗扰动能力。
定义系统状态变量:
(4)
式中:ωref为电机的参考转速。TL视为扰动转矩Td,对式(4)求微分可以得到:
(5)
式中:Td为扰动转矩。
(6)
为了达到无超调稳态,设计如下滑模面函数:
s=cx1+x2
(7)
式中:c为设计参数。
对滑模面函数求微分,可得:
(8)
2.2 基于变趋近速度的趋近率设计
传统方案一般采用指数趋近率函数式(9),保证电机运行阶段的速度动态品质。
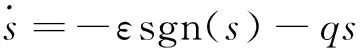
(9)
式中:sgn(s)为符号函数;ε,q>0。
结合式(8),可得滑模速度控制器表达式:
(10)
滑模控制器中包含不连续函数sgn(s),为了降低抖振,选择饱和函数sat(s)代替符号函数sgn(s),表达式转变:
(11)
其中饱和函数表达式:
(12)
式中:k为控制器增益,k>0。
为了使得控制系统扰动抑制能力更强,滑模面切换更加平滑,对趋近率的趋近速度进行重新设计。
传统滑模控制趋近率中,指数项为-qs,负责当系统远离滑模面时,将系统快速逼近切换面;等速项为-εsgn(s),负责系统到达滑模面附近时速度不为0,维持滑动状态,保证系统能够到达滑模面。结合引入的饱和函数,本文的改进趋近率:
(13)
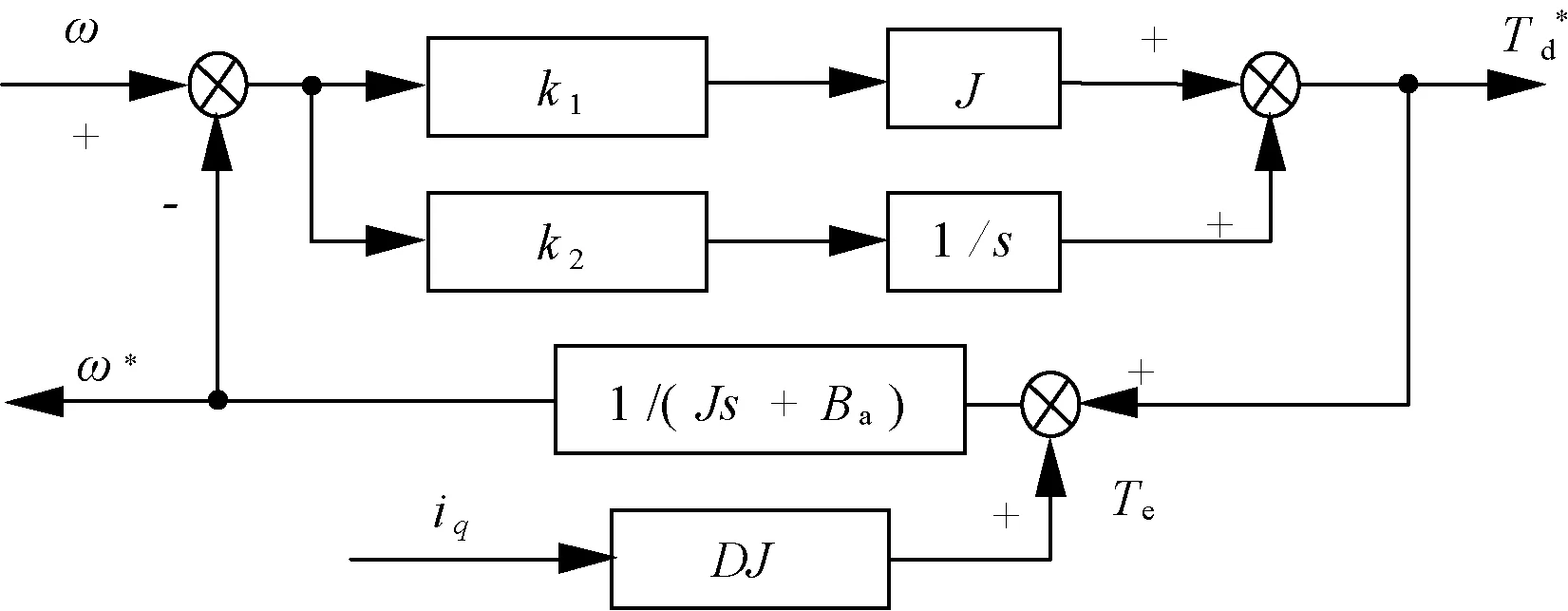
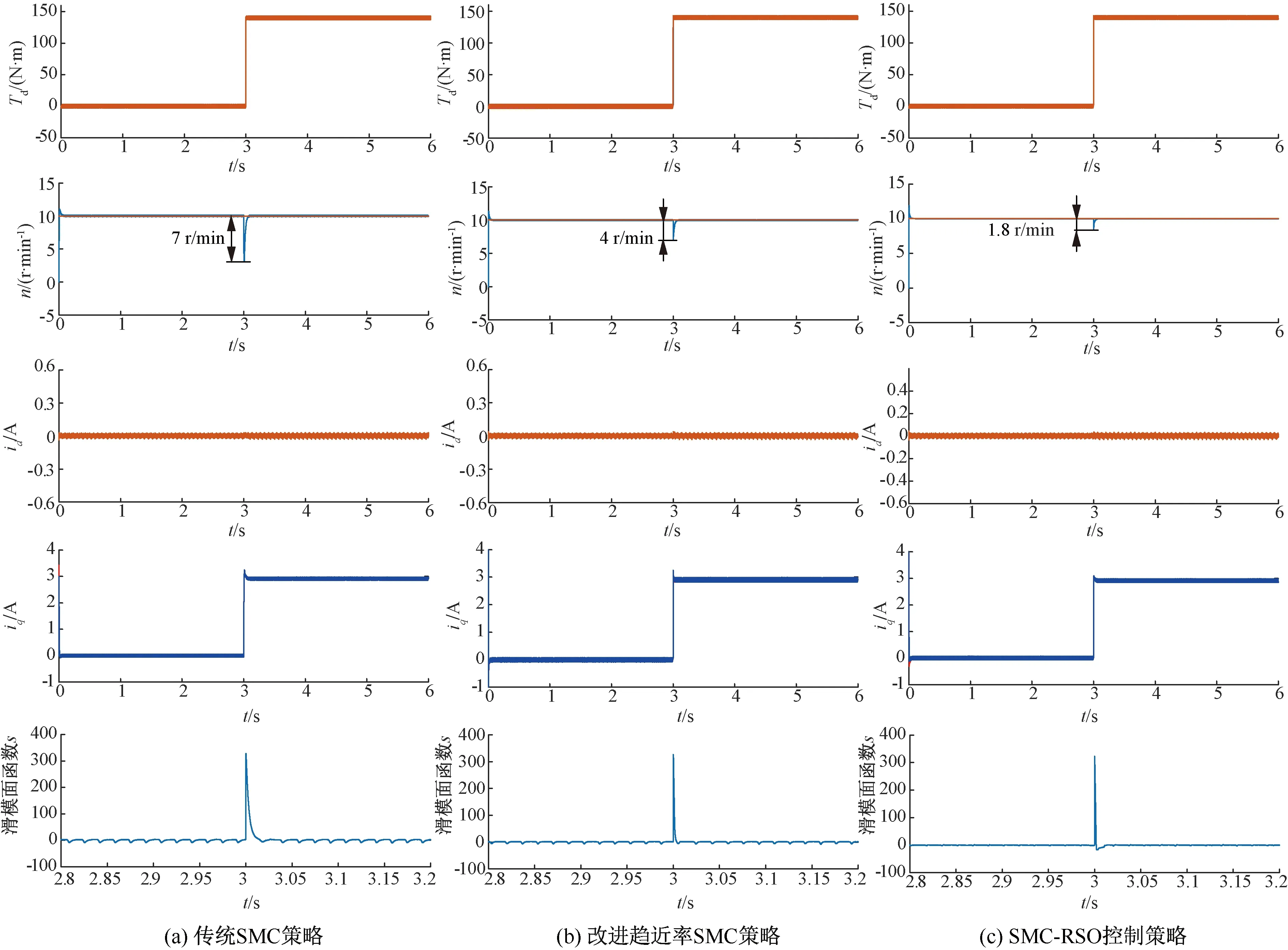
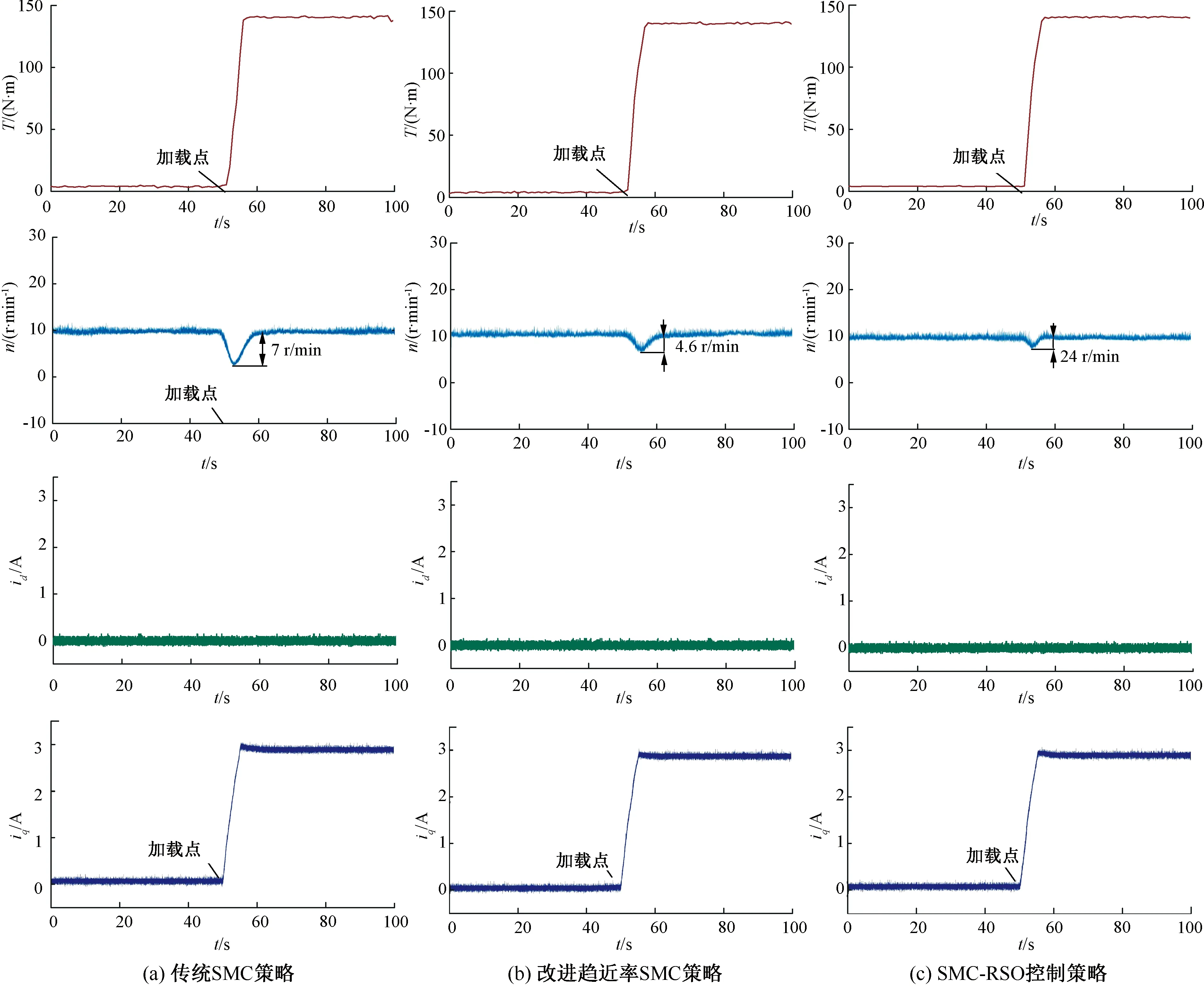
式中:0 (1)当系统离滑模面较远,即|s|→∞时,传统趋近率中指数项占主导因素,而在本文的趋近率中,此时f(s)→n,等速项趋近速度变为原本的n倍,同时指数项较传统趋近率增加为n倍,趋近速度大大提高,提高了系统趋近过程的快速性,使得系统发生扰动能够快速返回平稳状态。 (2)当系统接近滑模面,即|s|→0时,此时指数项接近0,趋近速率由等速项决定。由于m取值小于1,此时系统趋近率为原本传统趋近率的m倍,当系统在滑模面附近上下切换时,可以有较为平滑的切换过程,速度调节更加平稳,系统抖振降低。经过仿真分析,取值n=3,m=0.5。 此时表达式转变: (14) 如此,电机在速度控制的过程中能够获得更加平滑的滑模面切换状态。 -εsf(s)sat(s)-qs2f(s) (15) 当ε、q均大于零时,系统渐进稳定。 综上,设计滑模速度控制结构框图如图1所示。 图1 滑模控制器结构图 可以得出,设计的滑模观测器并不需要转矩扰动信息,结构设计简单,同时包含积分环节,能够有效降低抖振,消除稳态误差。 在调速控制时,电机的位置信号可以使用旋变或者编码器实测值,因此观测器设计过程中,只需观测电机的转速和转矩信息。采用降阶状态观测器(以下简称RSO)的方式,能够有效降低观测器设计时的参数复杂度。 (16) (17) 转子位置为转速的积分,因此在观测器设计环节可以不考虑对转子位置的观测,这样就可以实现降阶的目的。仅考虑转速和负载转矩的降阶观测器状态方程: (18) 将运动方程转化到s域中,可得: (19) 此时,基于观测器的状态方程在s域中改写: (20) 当状态观测器经过配置后,准确观测电机转速时,对照式(19)和式(20),得到: (21) 如此,便可实时观测电机负载转矩。同时,可以得到前馈电流iq2: (22) 综上,q轴电流参考值可以表示: (23) 图2为设计得到的RSO结构示意图,图3为与改进趋近率滑模控制结合后的永磁直驱伺服电机滑模与扰动补偿整体控制结构框图。 图2 RSO框图 图3 永磁直驱电机滑模控制策略框图 为验证本文提出的基于前馈补偿的永磁直驱电机抗扰动滑模控制策略,在MATLAB/Simulink软件中搭建了仿真模型,对扰动抑制控制策略进行了对比仿真,并在永磁直驱伺服电机系统实验平台上进行了实验对比研究。表1为仿真模型与实验平台的相关参数。 表1 仿真与实验平台参数 在3 s时对电机突加140 N·m负载转矩,电机给定转速10 r/min,仿真结果如图4所示。图4(a)给出了传统滑模控制(以下简称SMC)策略的抗干扰性能响应曲线,图4(b)给出了改进趋近率滑模控制策略的扰动抑制能力响应曲线,图4(c)则是提出的SMC-RSO控制策略下电机扰动抑制性能响应曲线。从图4可以看出: 图4 不同滑模控制策略的仿真结果对比 (1)在改进趋近率SMC策略时,相较于传统SMC策略7 r/min的转速跌落,电机转速波动得到更为明显的抑制,加载点速度跌落达到4 r/min,同时,滑模面函数在突加负载时恢复时间减少,有效提升了电机运行时的鲁棒性。 (2)在增加了转矩扰动前馈补偿之后,采用SMC-RSO控制策略的直驱控制系统具有更高的抗干扰性,与单独SMC策略相比,滑模切换面更为平滑,滑模面函数波动大大降低;加载时,转速掉落从4 r/min降低到1.8 r/min,同时d、q轴电流响应也能够准确跟随电流给定值。仿真结果证明,基于滑模与前馈补偿的控制方法可以有效地实现对扰动转矩的抑制作用。 为了对本文的转矩扰动抑制策略进行实验验证,搭建了如图5所示的永磁直驱伺服电机实验平台,主要包括磁粉制动器、联轴器、转速转矩传感器、测试用L钢架、增速机、冷却系统等。控制器硬件主要包括主功率电路、采样调理电路、保护电路、DSP控制电路等。 图5 实验平台实物图 首先对电机转矩扰动观测器性能进行实验,在电机闭环运行状态下对电机实际转矩进行观察,并与控制器输出转矩进行对比,所得扰动结果对比波形如图6所示。 图6 实际转矩与估测转矩比较 对电机扰动抑制策略进行验证,磁粉制动器加载,折算后电机负载转矩140 N·m左右,观察转矩传感器折算后输出曲线与电机估测转矩曲线,可以看到,控制器输出的估测转矩能够跟上负载转矩变化,验证了本文设计RSO的有效性,满足实验所需对转矩扰动进行前馈补偿的要求。 在相同给定条件下对传统SMC策略、改进趋近率SMC控制策略以及增加前馈补偿的SMC-RSO控制策略进行实验验证。图7给出了三种不同控制策略在相同扰动下的响应曲线对比结果。从上到下依次给出了施加的转矩、转速响应、以及d、q轴电流波形。从图7中可以看出,在电机受到磁粉制动器加载影响后,在滑模控制策略下,电机的转速跌落约为7 r/min,有较大的转速跌落情况;而在改进趋近率SMC策略下,电机的转速跌落约为4.6 r/min,与传统SMC相比,电机转速波动得到了有效的抑制;而在增加了前馈补偿之后,电机转速波动下降为2.4 r/min左右,电机正常运行基本不受影响。综合来看,采用SMC-RSO控制策略时,电机在扰动影响下的鲁棒性更强,验证了本文设计的SMC-RSO扰动抑制策略的可行性与有效性。 图7 不同滑模控制策略的实验结果对比 本文设计了永磁直驱电机的速度滑模控制器,通过改进系统趋近率设计,降低了抖振影响并使得滑模面切换更加平滑。在此基础上,引入RSO模块,对电机的转矩扰动进行了实时观测,并增加了前馈补偿环节,进一步提升了对电机转矩扰动的抑制能力。在永磁直驱伺服电机系统仿真与实验平台上,开展相关验证,获得以下结论: 1)通过对不同滑模状态下系统的趋近速度进行重新设计,提升了系统在滑模面附近切换时的平滑性,削弱了抖振影响,提升了速度控制的平稳性; 2)设计的RSO能够实现对系统复杂扰动下的扰动转矩准确观测,同时观测器参数设计较为简单; 3)通过设计改进趋近率与RSO前馈补偿组合的控制方案,提升了多种扰动下特别是负载突变时的扰动抑制效果; 4)仿真与实验证明,基于前馈补偿的永磁直驱电机抗扰动滑模控制策略是有效可行的,可以明显改善外部扰动下系统速度控制的平稳性。2.3 改进滑模控制器稳定性分析


3 降阶转矩观测器设计

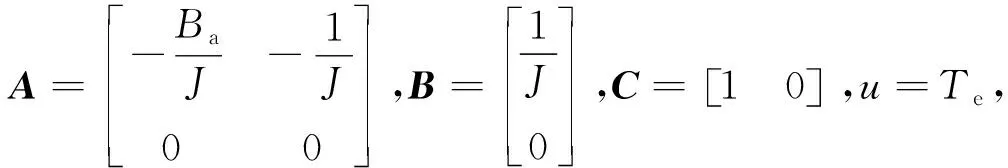

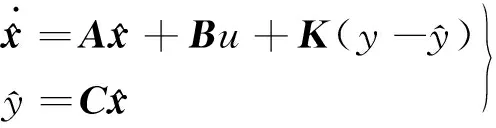


4 仿真与实验
4.1 仿真验证
4.2 实验验证


5 结 语
