基于功能安全的双冗余旋转变压器软件解码研究

李晓杰

(威迪斯电机技术有限公司，上海 201801)

0 引 言

随着世界能源和国际形势的日趋紧张，各国都在大力研究和发展新能源汽车，永磁同步电机因高功率密度等优越性，成为新能源汽车中的主流驱动电机。永磁电机控制的关键是需要强实时、高精度地获取转子位置，文献[1]对此进行了研究测试，验证了转子角度偏差对于永磁同步电机的运行性能有明显的降低。目前获取转子位置的主要方式有电涡流传感器、巨磁阻传感器、旋转变压器(以下简称旋变)，其中旋变相对于前两种方式表现出更强的抗干扰性和稳定性，被广泛地应用于车用永磁电机上。

根据功能安全的需求，扭矩安全的目标至少是ASIL(汽车安全完整性等级)C，甚至ASIL D。按照需求分解，对于角度传感器的安全等级往往是ASIL C。使用一块外置的硬件解码芯片和电机控制器MCU的软件解码算法是实现ASIL C安全等级一种较为广泛的方案，其中解码芯片多使用多摩川的AU680x系列，ADI的AD2S1210系列。正常运行时电机控制器使用MCU的软件解码得到的角度，同时使用硬件解码得到的角度进行校验，如果两者按照诊断算法认为失步，那么电机控制器根据条件进入安全状态。但上述的专用硬件解码芯片主要由欧美垄断，国产还是空白，国际形势的问题很容易引起缺芯停产，因此本文提出了一种不使用硬件解码芯片但符合功能安全需求的双冗余旋变解码方案，既节省了硬件的成本，也减少了芯片依赖性。

共因失效(Common Cause Failure)定义为由同一种应力(原因)导致的一个以上的相同部件、模块、单元或者系统发生的失效。如果单纯地通过冗余使用双路Δ-Σ ADC采样旋变反馈信号便会产生共因失效，比如Δ-Σ ADC内核出现[2]：基准电压断开连接/受损，输入/输出缓冲器/PGA受损，DC内核受损/饱和，内部稳压器电源不正确。此时，双冗余的Δ-Σ解码方式便串联失效了。鉴于此，本文通过Δ-Σ ADC和SAR ADC两种的不同ADC采样模块来实现双冗余旋变的软件解码。

1 Δ-Σ ADC旋变解码原理

旋变的激磁信号和反馈信号如图1所示，信号可以表示：

图1 旋变激磁信号与反馈信号

式中:Uamp为激磁经过旋变后的差分电压幅值；ω为激磁信号角频率；θ为旋变转子的角位置。

以英飞凌的AURIX单片机为例，Δ-Σ ADC首先通过SPWM波发生器产生载波频率为312.5 kHz、信号频率为9.765 625 kHz的SPWM波，随后通过截止频率15 kHz的板载IIR低通滤波器，即可得到周期102.4 μs的标准激磁信号。在反馈采样环节，首先通过高频的过采样模块采样瞬态的旋变信号的反馈幅值，再经过CIC滤波和两级FIR滤波将高频噪声滤除，即可得到信噪比较高的旋变幅值的瞬态反馈信号。在得到了旋变的瞬态信号后，再经过Δ-Σ ADC模块为旋变解码专门设计的整形器、积分器便可得到旋变的包络面。整形器的作用是根据旋变的激磁信号和反馈信号计算整个前馈通路的载波信号相位延迟，因为在激磁SPWM发出后经过了硬件的IIR滤波电路以及Δ-Σ ADC内部的三级低通滤波，必然导致了相位滞后。积分环节的作用是对激磁的一个周期的信号进行积分，将积分结果作为该激磁周期的旋变包络面[3-4]。

旋变解码的关键在于最后的整形和积分环节，如果整形相位不匹配，那么便会导致积分过程中的有效信号正负抵消，如图2、图3所示。图2的反馈信号能够完整地获取负半周信号，而图3只能获取部分负半周信号，这就导致积分后得到的包络面幅值变小，精度变低，相位也会发生变化。

图2 反馈整形过程

图3 整形错位波形

经过上述步骤之后便得到了旋变的正余弦包络面，可以总结步骤如下：

1)过采样旋变反馈的正余弦信号，一般至少过采样8倍以上；

2)对过采样的信号进行周期整形；

3)对整形后的信号进行积分。

2 SAR ADC旋变解码原理

由于和Δ-Σ ADC的采样原理上有较大的不同，并且SAR ADC没有硬件的整形器和积分器，所以本文提出了一种峰-峰值采样法进行旋变信号的软件解码。

如图4所示，在每一个旋变的激磁周期内，分别通过ADC采样旋变激磁信号的波峰和波谷值，随后以第一个采样值作为采样的符号基准，每隔一个取一个负号，随后两者相加作为当前激磁周期的正余弦反馈包络面。

图4 峰值采样法

考虑到旋变的频率在10 kHz，而电机低速时电频率要远小于500 Hz，在低速时可以取2～3个历史周期的值再进行平均处理，作为当前计算周期的正余弦包络面，这种解码方法对电机控制的主控芯片有极少的外设限制，通用性强，同时又通过类似于Δ-Σ ADC的过采样方式，能够提高采样的信噪比，提高解码后调度的抗噪性。

同样以英飞凌AURIX单片机为例，通过GTM的ATOM模块设置和旋变激磁周期同频的双边沿触发信号，每个触发信号均触发一次AD采样，在AD采样完成后触发DMA的搬运，DMA自动将AD采样结果搬运到指定内存区用于软件的计算，触发机制如图5所示。

图5 GTM和ADC触发机制

基于上述配置后，还需要通过离线标定的方式把ATOM通道的AD触发点和旋变反馈信号的波峰进行对齐，步骤如下：

(1)对GTM的ATOM通道按照步长逐渐从0开始设置触发点，例如ATOM通道按照100 MHz，计数周期为10 240，第一次设置触发点在计数器0和5 120处，记录当前的采样值，第一次设置触发点在计数器10和5 130处，记录采样值。如此递增，得到了512个采样值。

(2)遍历步骤(1)中得到的512个采样值，以采样最大值为ATOM通道和激磁信号的固定偏移量。

(3)将电机转子转过一定角度后重复步骤(1)和步骤(2)中的操作，多次取平均后写入GTM的ATOM通道内为最终的采样偏移量。

通过上述方法后即可得到抗噪能力较强的正余弦包络面。对比SAR ADC和Δ-Σ ADC获取包络面的方法，其本质完全相同，都是通过过采样、整形、积分三个基本环节实现了包络面的解析。

3 正余弦包络面的矫正

上述已经获得了正余弦的包络面，但考虑到实际旋变安装时的偏差、信号传递过程中的非对称衰减等因素，包络面必然存在一定的失真，不能直接送入锁相环。文献[5]提到了包络面的失真可能会导致锁相环的角速度存在低阶波动，以二阶波动为主，而作为角速度积分得到的电角度自然也存在着波动。而文献[6-8]提到的双二阶广义积分虽然能有效地剔除包络面的畸变，但算法过程复杂，同时车用永磁电机的转速范围很广，无法全范围提取并抑制负序分量。本文针对Δ-Σ ADC和SAR ADC分别提出了较为简单的包络面矫正方法。

3.1 Δ-Σ ADC的包络矫正

考虑到Δ-Σ ADC内部存在直流矫正且过采样率较高，包络面的失真主要来自于角度和电流采样点的时间延迟[4]，因此通过AURIX单片机的GTM模块的TIM通道分别捕获Δ-Σ ADC和电流采样点的时间差，再根据当前机械转速可以计算得到两者的相位差，随后根据三角和差公式进行相位补偿，如图6所示。

图6 Δ-Σ ADC包络面矫正环节

3.2 SAR ADC的包络矫正

SAR ADC是通过软件实现整形和积分，采样率也较低，但一般和相电流同时采样，所以SAR ADC的峰-峰值采样方式的包络失真主要在于幅值偏差和零位偏差。对此主要通过离线方式对幅值和零位进行标定，步骤如下：

(1)利用测功机将旋变对拖，保持在一个较低的转速，如500 r/min。

(2)软件将采样到的正余弦包络面先进行低通滤波，截止频率5 kHz。随后连续采样100个电周期后遍历采样的数据，获取正弦幅值的最大值、最小值，然后根据最大值最小值计算幅值和零位偏差：

式中：Amax、Amin为正弦幅值的最大值、最小值；A为幅值；O为零位偏差。

离线标定完成后将数据固化到程序中对SAR ADC的采样数据进行矫正，如图7所示。

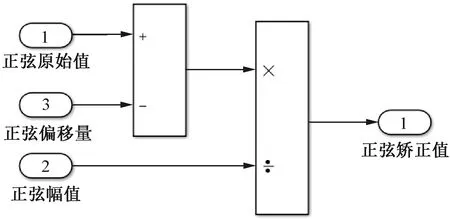
图7 SAR ADC包络面矫正环节

余弦的标定和矫正方式和正弦一致，不再赘述。

通过上述矫正之后，正余弦的包络面便可送入角度观测器进行锁相计算角度。

4 角度观测器设计

角度观测器有二阶和三阶观测器。二阶观测器参数整定简单、不容易积分饱和，但在电机加速运行过程中锁相角度和真实角度存在一个稳态误差；三阶观测器虽然参数整定较复杂，但能够在电机加速运行时依然无稳态误差地跟踪真实的电机角度[9-10]。因此，本文使用三阶观测器进行设计，三阶观测器的结构如图8所示。

图8 三阶观测器结构

当观测得到的α和包络面θ接近时，可认为sin(θ-α)≈θ-α，可推得闭环传递函数：

按照劳斯-赫尔维茨稳定判据，该三阶系统稳定的条件[8]：

该传递函数共有3个极点，按照一个复实数极点和一对主导极点进行设计，可以转化成如下的形式：

式中：ξ表示阻尼比；ωn为自然频率；K为负实数极点的位置调节系数。

取系数K=10，此时整个系统的响应接近于极点为相同主导极点的二阶系统，按照二阶最佳阻尼比ξ=0.707，此时可得：

自然频率和传递函数的带宽呈正比例关系，一般要求观测器带宽不低于电流环带宽即可，带宽过高会导致传递函数离散化后响应畸变甚至发散，这里取ωn=200π(rad/s)，零极点分布如图9所示。

图9 观测器零极点图

通过MATLAB仿真得到系统的阶跃响应如图10所示，响应时间为10 ms，超调量11.9%。角度跟踪结果如图11所示。

图10 阶跃响应波形

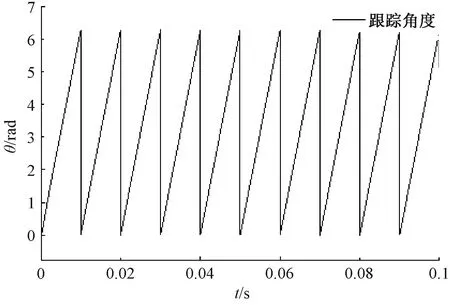
图11 角度跟踪波形

5 实验结果与分析

在完成上述设计和仿真工作后，本文的方案在台架上进行了验证，实验台架如图12所示。

图12 实验台架

为了验证软件解码的稳定性，另外增加了多摩川的AU6805硬件解码芯片。激磁信号统一使用英飞凌AURIX单片机产生的激磁信号，经过放大电路后送给旋变，经过旋变调节后，由本文的两种解码方式和硬件解码同时进行采样和解码，最后通过CAN报文将角度数据发出并处理。

测试方法：通过测功机将被测电机控制在稳定的转速，理论上在固定转速且固定的采样周期下，电角度的增量应该是相同的，通过考量固定周期下角度增量的稳定性可以定量分析解码的稳定性，数据如表1所示(表中角度统一折算到电角度0～360°，采样周期为50 μs读取一次解码角度，电机极对数为4)。

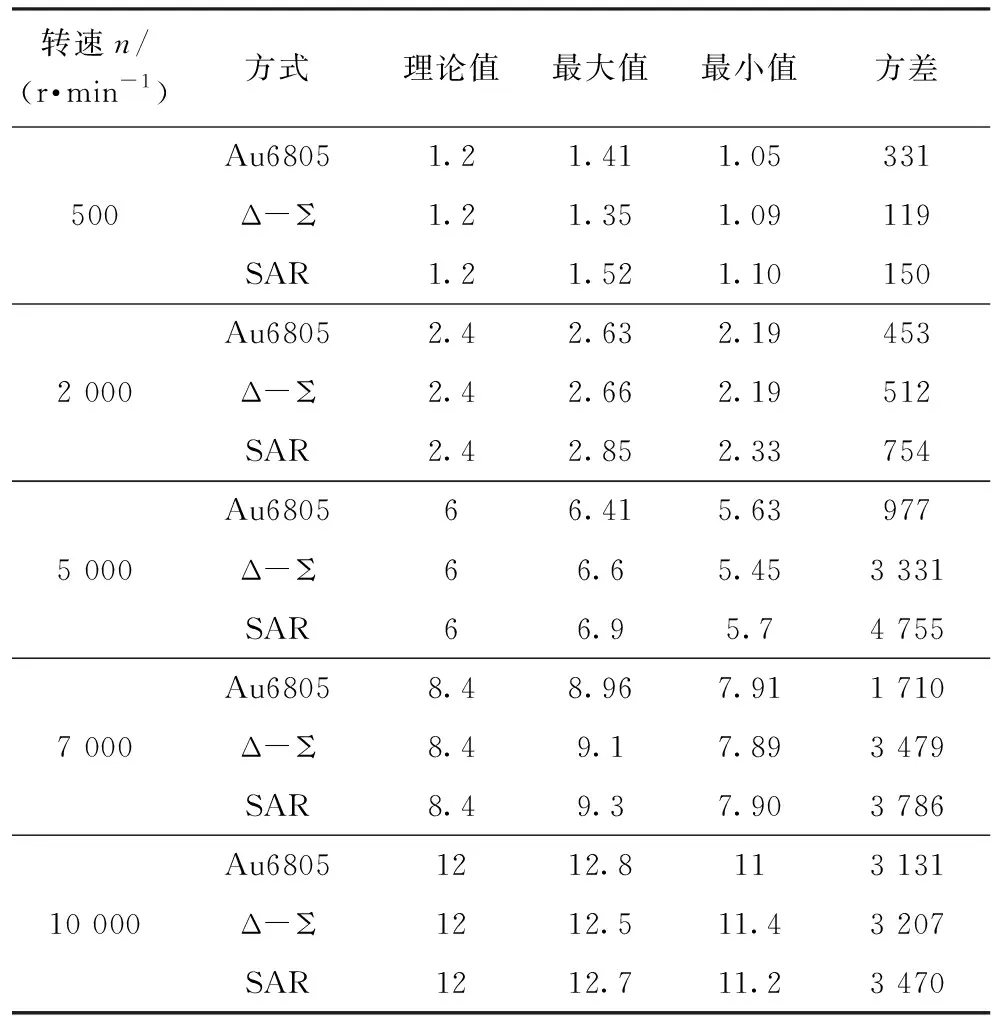
表1 解码效果对比数据

2 000 r/min下硬件解码与SAR ADC、Δ-Σ ADC的角度误差如图13、图14所示。

图13 2 000 r/min硬件解码与SAR ADC角度误差

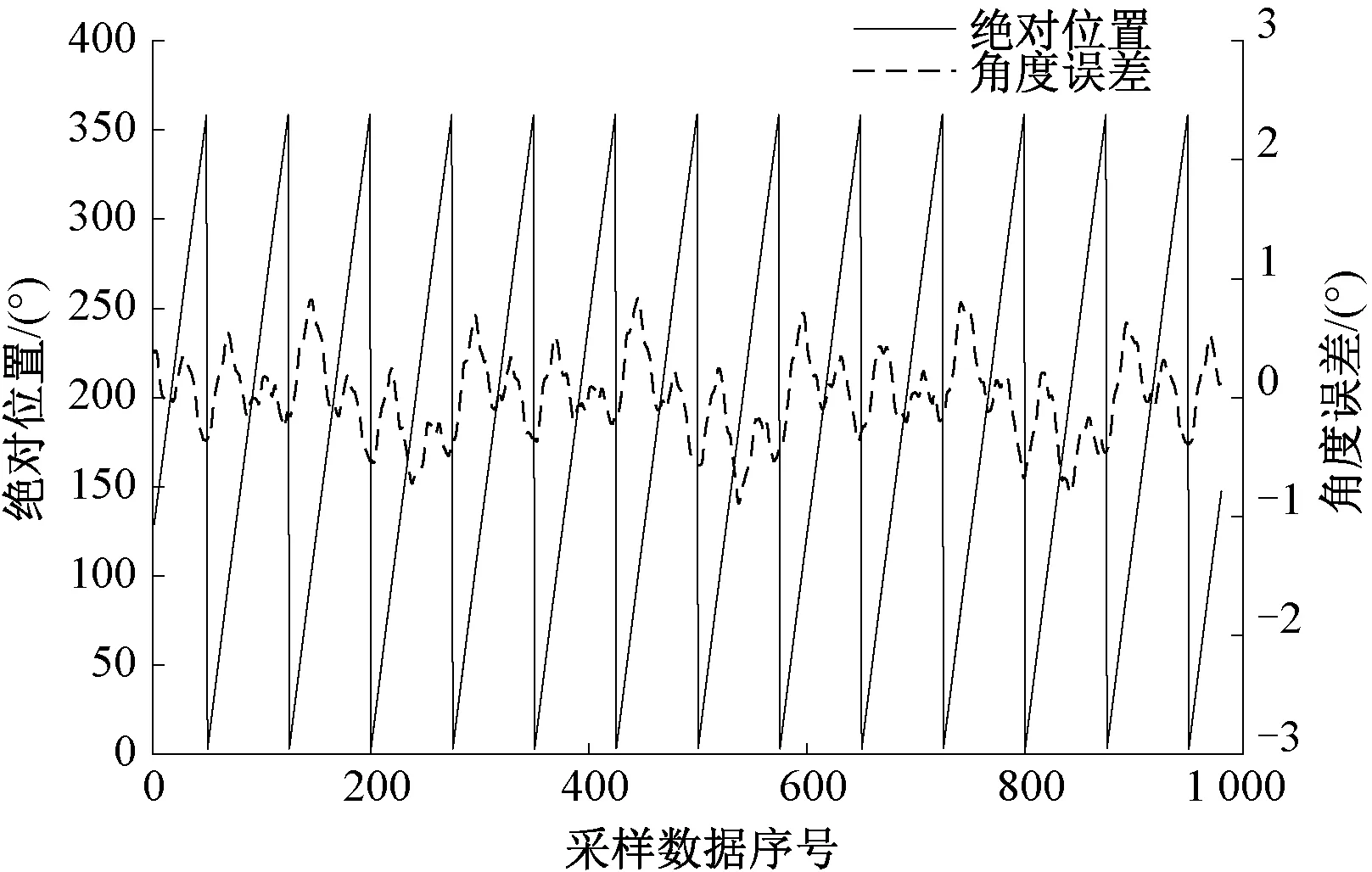
图14 2 000 r/min硬件解码与Δ-Σ ADC角度误差

6 结 语

在中低速段Δ-Σ ADC和SAR ADC两种软解码的稳定性要略差于硬件解码，但在高速段软件解码和硬件解码的性能几乎可以持平。

得益于硬件外设的先天优势，Δ-Σ ADC相较于SAR ADC的解码效果稳定性要更好。

在全转速段两种软解码的最大相对误差都能把相对的角度误差控制在1°以内，实际大部分时候均在0.3°以内，可用于稳定的永磁电机控制。

综上，本文的方案完全可用于有功能安全需求的电机控制系统中，通过两种解码方式的双冗余可实现更高的故障覆盖度，有较强的应用价值。