基于CSAEMD-KECA和角结构距离的齿轮故障识别方法*

高庆云,郭 力,陈长华

(1.杭州职业技术学院,浙江 杭州 310018;2.重庆交通大学 机电与车辆工程学院,重庆 400074;3.重庆长江轴承股份有限公司,重庆 401336)

0 引 言

由于机械设备的振动信号总是包含着丰富的信息,从中可以了解机械设备的运行状态。毫无疑问,基于振动信号处理的故障诊断技术对于监控关键结构或设备的健康状况至关重要[1]。一般来说,传感器用于获取机械振动信息,从这些信息中,人们可以获取机械设备运行状态的特征[2]。

在对机械设备进行智能故障诊断时,提取到的原始振动信号中通常会存在噪声的成分,需要一种模式分解方法对原始信号进行分解重构,从而减少噪声信号对智能故障诊断分类过程的干扰。

在机械设备原始信号分解方面,经验模式分解方法(empirical mode decomposition,EMD)是一种常用的信号分解方法。通过EMD分解,振动信号可以被分解成一系列的固有模态函数(intrinsic modal function,IMF)。MENG De-biao等人[3]采用EMD方法,对风电机组滚动轴承的故障信号进行了分解,然后对分解后的数据进行了时域和频域上的特征提取,提高了滚动轴承故障诊断的准确率。SUN Yong-jian等人[4]提出了一种基于EMD和改进切比雪夫距离的滚动轴承故障诊断方法,采用EMD方法,将其信号分解为几个IMF,然后利用改进的切比雪夫距离方法,实现了对轴承的故障诊断。HANG Dong-ying等人[5]提出了一种基于EMD、粒子群优化支持向量机(particle swarm optimization support vector machine,PSO-SVM)和分形盒维数3种方法相结合的故障诊断方法;该方法首先采用EMD,将齿轮原始振动信号分解成了若干个IMF,然后分别从时域、频域、能量域和分形域计算了其特征,最后将特征矩阵输入到PSO-SVM分类器中,进行齿轮故障分类,提高了齿轮故障分类的准确率。

然而,EMD分解是不稳定的,并且存在模式混合问题,这种问题导致某个IMF分量包含不同尺度信号,或者相似尺度信号存在于不同IMF中,使基于EMD的信号分解有可能丢失重要的特征信息[6]。

为了解决这一问题,ZHANG Xiao-bo[7]采用集成经验模式分解(ensemble empirical mode decomposition,EEMD),对小波包处理后的不同齿轮故障模式的信号进行了分解,得到了更为有效的故障信号,提高了齿轮故障诊断时的诊断精度和诊断效率。ZHAN Yu-jie等人[8]提出了一种基于EEMD和双向长短期记忆(bi-directional long short-term memory,BILSTM)的多轴承寿命预测方法;该方法先利用EEMD,将原始振动信号分解成了有限个IMF,然后通过相关性准则和峭度信号的重构,对重构信号进行时域和频域上的特征选取,最后在选取的特征集上训练BILSTM网络,实现了轴承的剩余寿命预测。MA Biao等人[9]提出了一种基于EEMD能量熵和SOM神经网络(SOM neural networks,SOM-NN)的故障诊断新方法;该方法首先利用了EEMD方法,将齿轮在各种状态下的原始振动信号分解为若干个本征模态函数IMF,并计算了每个IMF的能量值和信号的能量熵,然后选取IMF能量占比和信号能量熵,组成一组能够反映故障振动信号的特征,最后将这些特征值输入SOM神经网络中,进行故障分类,提高了齿轮故障识别的准确率。

EEMD是通过使用噪声来辅助信号的分解,从而缓解EMD中的“模式混合”现象[5]。但EEMD在背景噪声较强,且故障过早的情况下,其去噪效果并不理想。

为了尽可能地减少噪声信号在原始信号中的残余,陈克等人[10]采用在原始信号上加入了正负噪声的方法,以抵消信号中加入的噪声,减少了噪声分量的产生;此外,该方法也提高了其计算效率。这种方法被称为互补总体经验模式分解(complementary ensemble empirical mode decomposition,CEEMD)。

受加入噪声信号辅助分解思想的启发,笔者提出一种新的正弦波辅助分解方法(complementary sineassisted empirical mode decomposition, CSAEMD),通过对原始信号进行分解,即在原始信号上加入正负正弦分量信号,以此作为参考尺度,用来缓解模式混合。

在使用模式分解方法进行分解重构,获得了能够表征故障特征的信息特征后,机械设备故障智能诊断的一个关键环节就是,寻找一种准确率高、自适应强的故障识别方法。

在机械设备的故障识别方面,韩松等人[11]提出了一种基于主成分分析(principal component analysis,PCA)和支持向量机(support vector machine,SVM)的滚动轴承故障识别方法,提高了轴承故障识别的准确率。ZHU Jing等人[12]采用PCA方法,进行了滚动轴承的智能故障识别。LI Hua-ping等人[13]针对振动信号传输路径复杂,不同传感器位置对诊断结果影响较大,以及旋转机械故障诊断特征提取困难等问题,提出了一种基于PCA和深度信念网络(deep belief network,DBN)的故障诊断新方法。

PCA[14]是一种典型的线性降维方法,它将N维特征降维到k维上,用这些k维特征构成能够反映样本特征的新数据集。但是,由于齿轮的故障信号往往伴随着很多非线性特征,采用PCA进行齿轮故障模式的聚类识别时,往往会导致错误的聚类。

核主成分分析(kernel principal component analysis,KPCA)是通过引入核方法,将线性主元分析拓展到非线性的方法。KPCA的核心思想是将输入数据映射投影到高维特征空间,并通过分解其核矩阵,得到特征值和特征向量。KPCA常见的做法是选择特征值最大的前k个特征向量,然后进行后续操作。

然而,在选择特征向量时,KPCA方法通常以方差的大小作为标准,而方差的大小又取决于特征变量所携带的信息量。因此,在实际的应用中,采用这种选择方法并不能达到最佳的聚类效果。

核熵成分分析(kernel entropy component analysis,KECA)是JENSSEN R提出的一种新的特征提取方法[15]。与KPCA相同,KECA需要对输入数据进行分解,并得到其特征值和特征向量。与KPCA所不同的是,KECA选择对输入信号瑞利熵贡献值大的特征向量,并将输入信号投影到特征向量,形成全新的数据特征。KECA选取成分的过程中,不仅考虑了特征值的作用,而且考虑了对应特征向量的作用,因此,其考虑的因素更加全面。

利用KECA进行多种数据实验时,发现不同类别的数据间呈现明显的互成一定角度的特点(可称为角结构特点)。具体而言,在利用KECA进行多种数据分析时,不同类别的样本往往互相垂直,而相同类别的样本往往共线。

因此,笔者利用样本间的余弦值表征样本的相似性,进而进行聚类分析,称为基于角结构距离的聚类方法。

综上所述,笔者提出一种基于CSAEMD-KECA的齿轮故障识别方法。首先,采用CSAEMD对齿轮故障数据进行分解,去除原始信号中存在的噪声分量,并尽可能地保留其重要特征信息;然后,选择与原始信号相关最大的分量进行重构,获得能够表征齿轮故障特征信息的信号;接着,采用KECA方法进行特征提取,获得具有角结构特征的投影向量,并将CSAEMD分解重构后的信号向投影向量投影,得到包含齿轮故障信息的新数据集;最后,采用基于角结构距离的聚类方法进行聚类分析,实现对不同齿轮故障模式的聚类识别目的。

1 理论描述

1.1 EMD理论

经验模态分解(EMD)方法是由LEI Ya-guo等人[16]提出的。EMD可以把信号分解为多个IMF。IMF满足以下两个条件:

(1)极值的数量和零交叉的数量相差不能超过1;

(2)局部包络平均值为零。

IMF代表嵌入在信号中的简单振荡模式。基于任何信号包含不同的简单IMF的假设,笔者引入EMD方法将信号分解为IMF分量。

笔者对经验模式分解(EMD)方法进行研究。EMD方法的步骤如下:

(1)初始化r0=x(t),并且i=1;

(2)提取IMF分量ci,IMF分量提取的过程如下：

(a)初始化h(k-1)=ri-1,k=1;

(b)求h(k-1)的局部最大值和极小值;

(c)用三次样条线对局部极大值和极小值进行插补,形成h(k-1)的上、下包络;

(d)计算h(k-1)的上、下包络的平均最小m(k-1);

(e)hik=hi(k-1)-mi(k-1);

(f)如果hik是IMF,则设置ci=hik,否则转到步骤(b),然后k=k+1。

(3)定义冗余分量ri+1=ri-ci;

(4)如果ri+1仍然有2个极值点,然后执行步骤(2)i=i+1,否则分解结束,ri+1是冗余分量。

1.2 CSAEMD理论

正弦波辅助分解(CSA-EMD)方法是在EMD基础上进行改进的,其核心思想是构建一个复合正弦信号。其构造的正弦信号形式为:

(1)

式中:N—辅助信号中正弦波的数量;ci—第i个正弦波的幅值;fb—第i个正弦波的频率。

与CEEMD在原始信号上加入分布在整个频谱的高斯白噪声信号不同,CSAEMD加入正负两组与原始信号主要频率大致相等的正弦辅助信号,并进行分解,取这两组相同阶数的IMF平均值。如果只加入正的正弦分量,则会代入其他频率分量。

正弦波的设定标准如下:

因为CEEMD是根据准二元滤波器对齐IMF,以此来减少模式混合现象,同样也可以在原始信号上添加与原始信号主要频率大致相等的正弦分量作为参考模式,以提取出故障特征频率。辅助信号的频谱范围不能超过原始信号范围[flow,fhigh]。

相关研究表明[17],EMD相邻频率比大于1.4时,有较轻微的模式混合现象,因此,幅值信号的相邻频率比需要大于1.4。尽量将辅助信号的频率与原始信号的主要频率分量设为一致。当频谱的主要频率相邻频率比大于1.4时,则将正弦分量设为等于原始信号的主要频率;反之,则尽可能使其靠近原始信号的主要频率。

通过反复实验,结果表明:正弦波的幅值设定为原始信号平均幅值的6倍时,分解效果最好。

当正弦波振幅、频率确定,辅助信号即构造完成。其算法的具体步骤如下:

(1)首先使用快速傅里叶变换,分析原始信号的频谱,得到原始信号的主要频率分量;

(2)按相邻正弦分量大于1.4的标准,设定正弦辅助信号;

(3)将构建的正负正弦波信号分别加入原始信号中,使用EMD分别对加入正负正弦分量的两组信号进行处理;

(4)将两组信号分解得到IMF,按照对应阶数求其平均值,得到的IMF平均值,即为所求。

1.3 核熵成分分析理论

KECA的特征提取过程如图1所示。

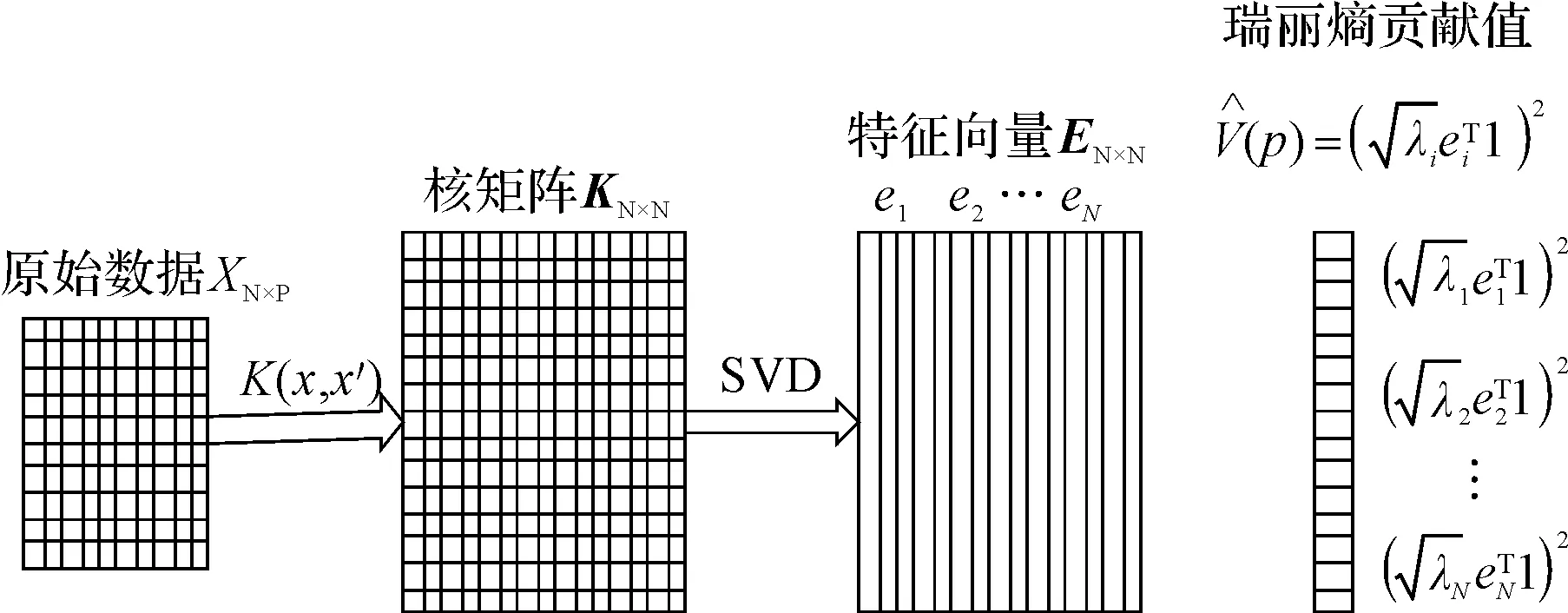
图1 KECA特征提取过程

从图1可以看出,KECA的具体步骤为:

(1)根据原始数据,确定核函数及其参数,计算原始数据的核矩阵K;

(2)由式K=EDλET对原始数据核矩阵进行分解,得到特征值和对应的特征向量(其中：Dλ—由特征值λ1,λ2,…,λN所组成的对角矩阵;E—对应的特征向量e1,e2,…,eN组成的矩阵);

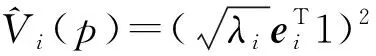
(4)计算主成分,TN×K=KN×NEN×K。

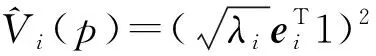
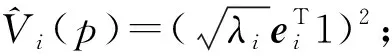
1.4 基于角结构距离的聚类方法

基于角结构距离的聚类过程如图2所示。

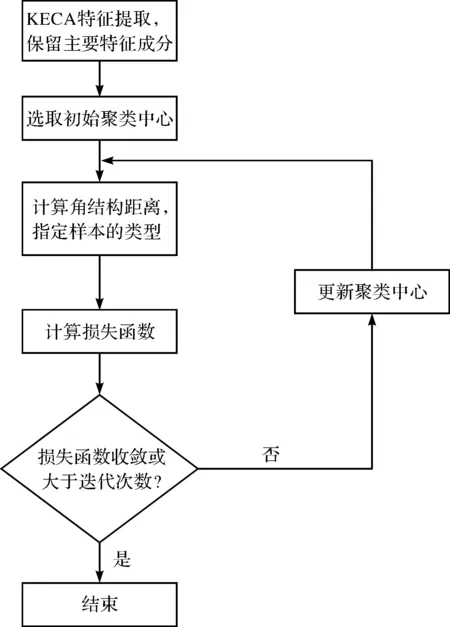
图2 KECA聚类流程图

从图2可以看出,KECA聚类的具体步骤为:

(1)利用KECA进行特征提取,即根据上述相关分析,计算特征成分,并获取主要的特征成分;

(2)初始化聚类中心mi,i=1,2,…,C;

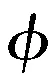
CS损失函数是测量核特征空间中数据集Φ的均值向量之间的cos值。例如,第i类样本的概率函数pi(x)和整体数据概率函数p(x)间的CS收敛函数可表示为:

Dcs(pi,p)=-logVcs(pi,p)

(2)

其中:

(3)

假设有来自于类别Ci,概率密度函数为pi(x)的Ni个数据点组成的数据集xi∈Di;来自于概率密度函数p(x)的N个样本组成的全体数据样本集。

在核特征空间中,基于角距离的损失函数可表示为:

(4)

(4)更新聚类中心mi,i=1,2,…,C;

(5)重复(3)和(4),直到收敛或者循环次数大于某一设定值(笔者设定收敛条件为J的变化小于10-3,循环次数的最大值为1 000)。

1.5 基于CSAEMD-KECA的计算流程

笔者提出的基于CSAEMD-KECA的齿轮故障识别方法,其计算流程如图3所示。

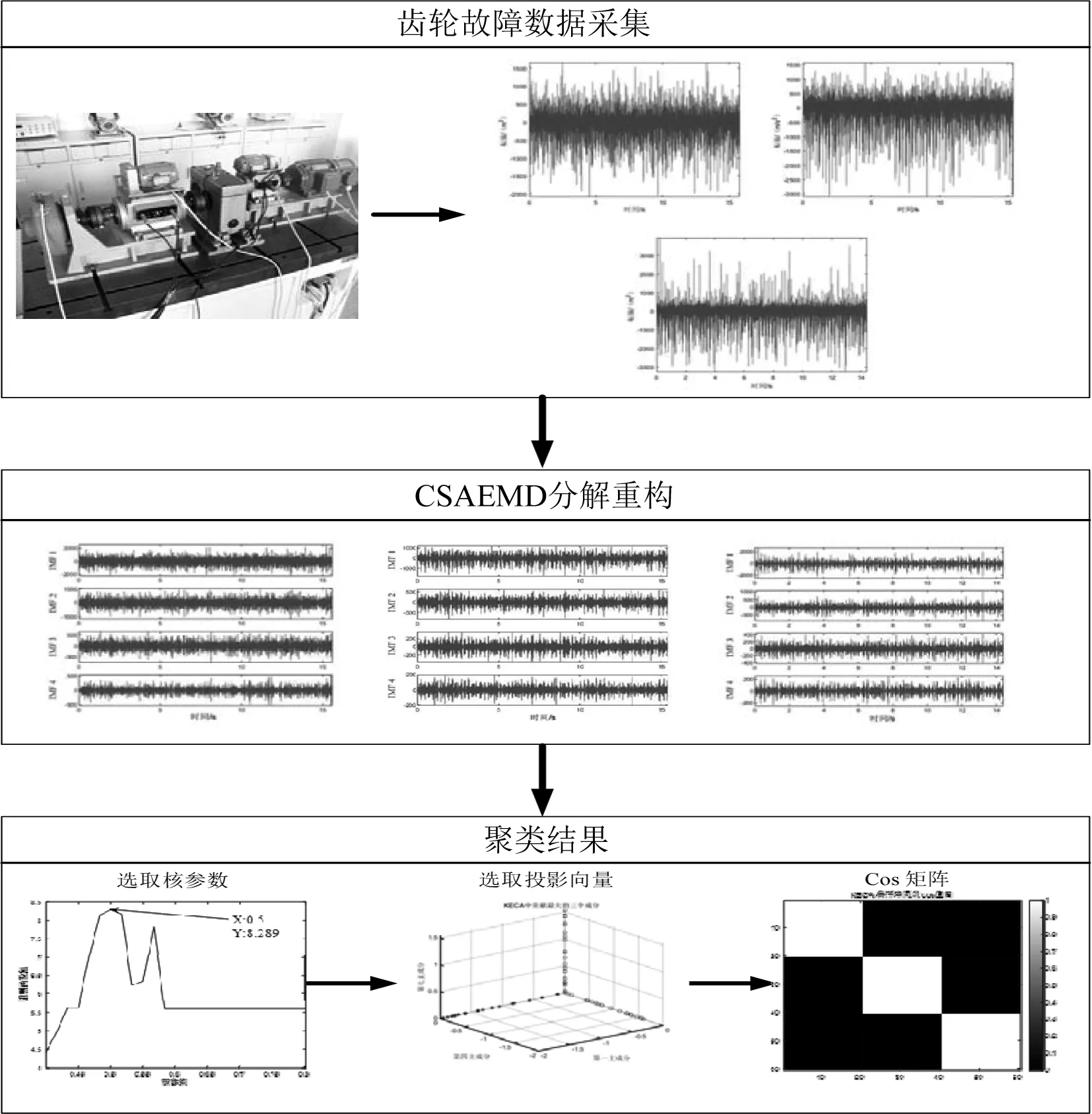
图3 基于CSAEMD-KECA方法计算流程

从图3可以看出,基于CSAEMD-KECA方法主要包括以下3个步骤:

(1)采用振动传感器采集不同故障状态下的齿轮振动数据;

(2)对采集到的齿轮振动数据,采用CSAEMD进行分解,选取相关最大的IMF分量进行重构;

(3)确定KECA的核参数,采用KECA对重构后齿轮的故障数据进行特征提取,并采用基于角结构距离的聚类方法进行聚类,以实现齿轮不同故障模式的聚类识别。

2 仿真分析

为了验证互补正弦辅助经验模式分解方法(CSAEMD)具有良好的分解性能,笔者对其进行数值模拟分析。

仿真信号由多个正弦分量和高斯白噪声组成,其具体形式为:

x1=sin(2×π×f1×t)x2=sin(2×π×f2×t)x3=sin(2×π×f3×t)x=x1+x2+x3+w(t)

(5)

其中,f1=45 Hz,f2=70 Hz,f3=110 Hz。仿真信号由3个正弦分量构成,为了使仿真信号符合实际要求在正弦分量信号上加入噪声信号。

仿真信号的时域图如图4所示。

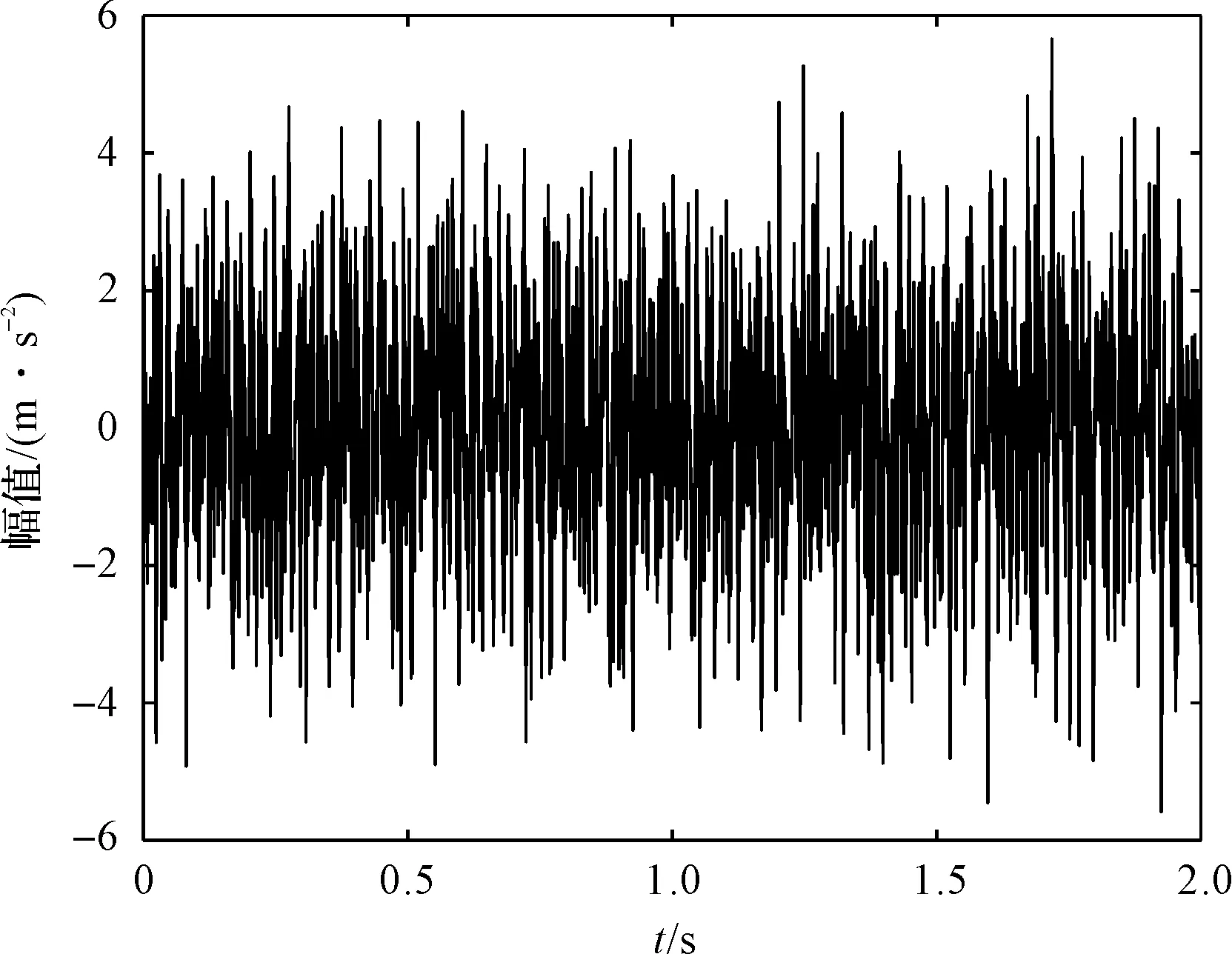
图4 模拟信号时域图

笔者采用EMD对模拟信号进行分解,得到EMD分解结果如图5所示。

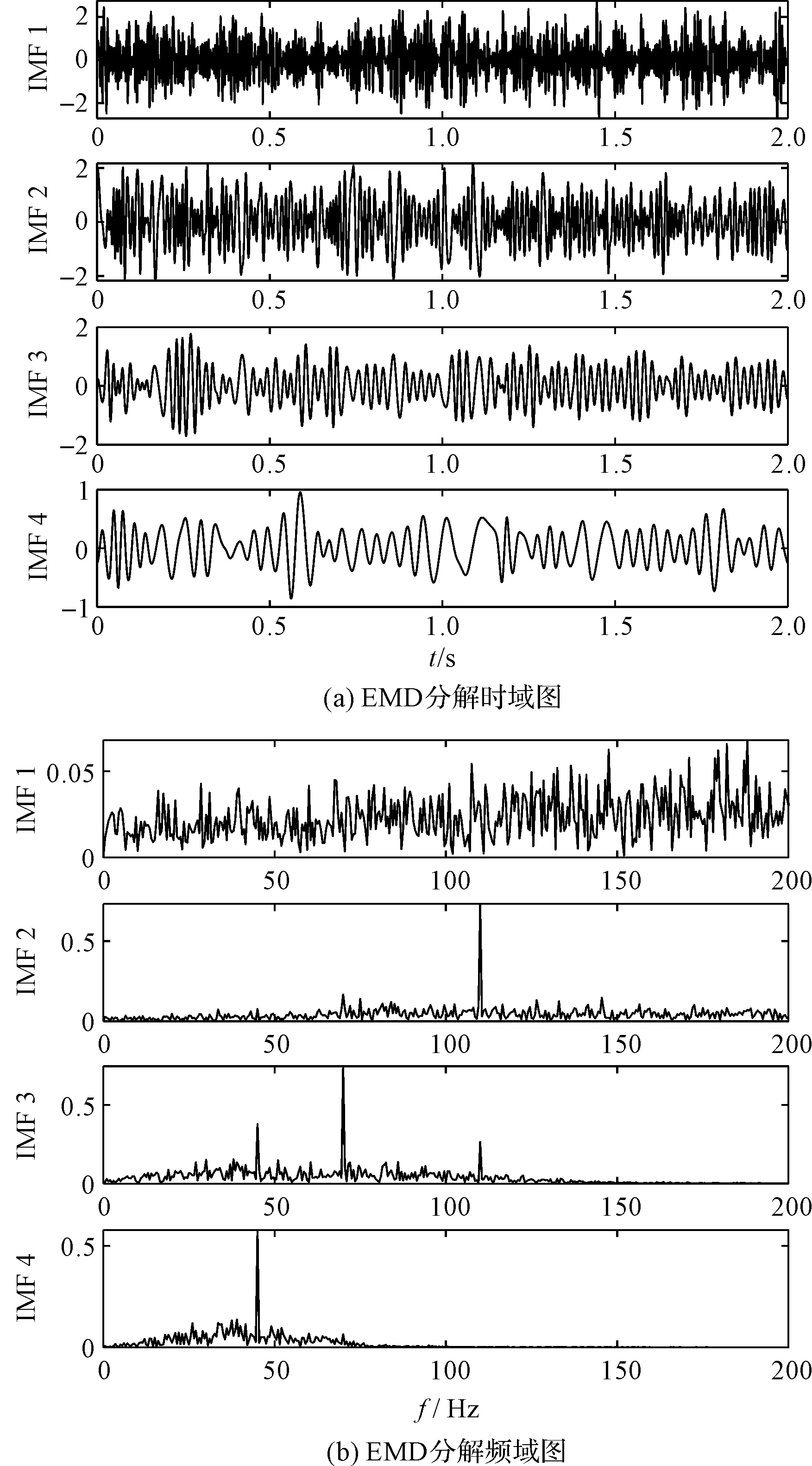
图5 EMD分解结果

由图5可知:通过EMD分解的IMF分量有较严重的模式混合现象;同时,IMF3和IMF4也包含频率45 Hz,频率110 Hz主要包含于IMF2,也少量包含于IMF3。

笔者使用CEEMDAN分解模拟信号,得到的CEEMDAN分解结果如图6所示。

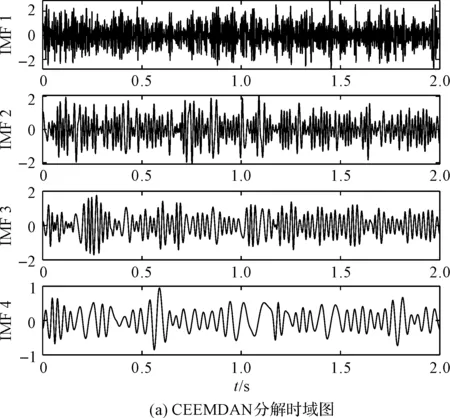
图6 CEEMDAN分解结果

从图6可以看出:CEEMDAN也有模式混合现象,IMF3和IMF2都包含了频率45 Hz,频率70 Hz既包含于IMF2,也少量包含于IMF1。

CSAEMD分解模拟信号得到CSAEMD分解结果如图7所示。

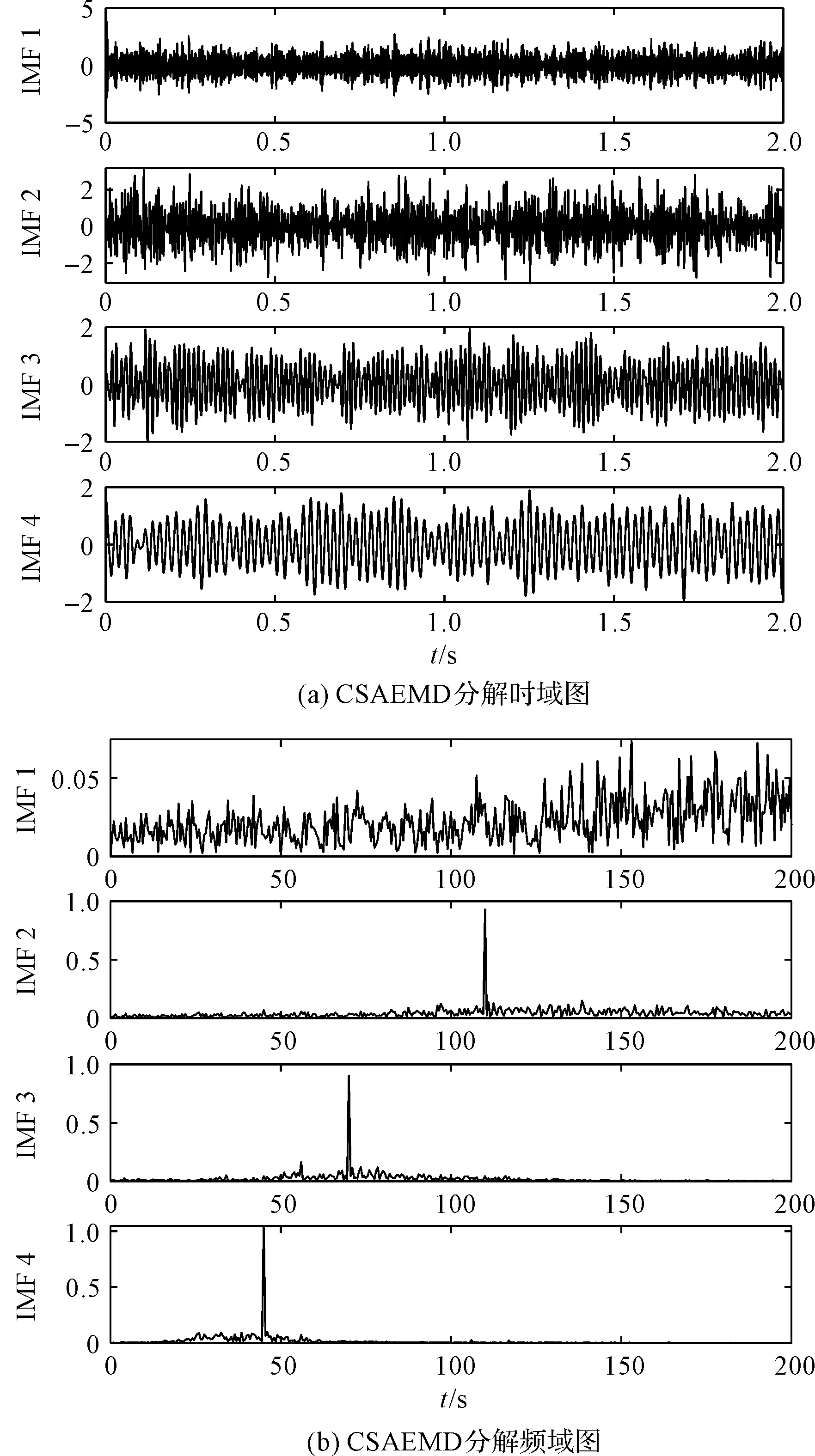
图7 CSAEMD分解结果

从图7可以看出:CSAEMD没有明显的模式混合现象,IMF 2、IMF 3、IMF 3分别包含频率45 Hz、70 Hz、110 Hz。

笔者通过仿真信号,验证了CSAEMD的优异分解性能,能减轻EMD存在的模式混合现象。

3 实验及结果分析

3.1 原始信号的分解重构

为了进一步验证上述方法的可行性,笔者搭建了故障模拟实验台,并在故障模拟实验台上采集实际数据。

故障模拟实验台主要由电机、联轴器、齿轮箱、轴承、制动器组成。

实验台的实物图如图8所示。

图8 齿轮故障综合实验台

实验台中的齿轮位于齿轮箱里面。笔者将振动传感器置于齿轮箱外面进行数据采集,主要采集正常状态、齿轮断齿、齿轮磨损3种不同故障模式下的振动信号。实验中的采样频率设置为2 000 Hz。

实验获得实际信号中,正常状态齿轮的时域图如图9所示。

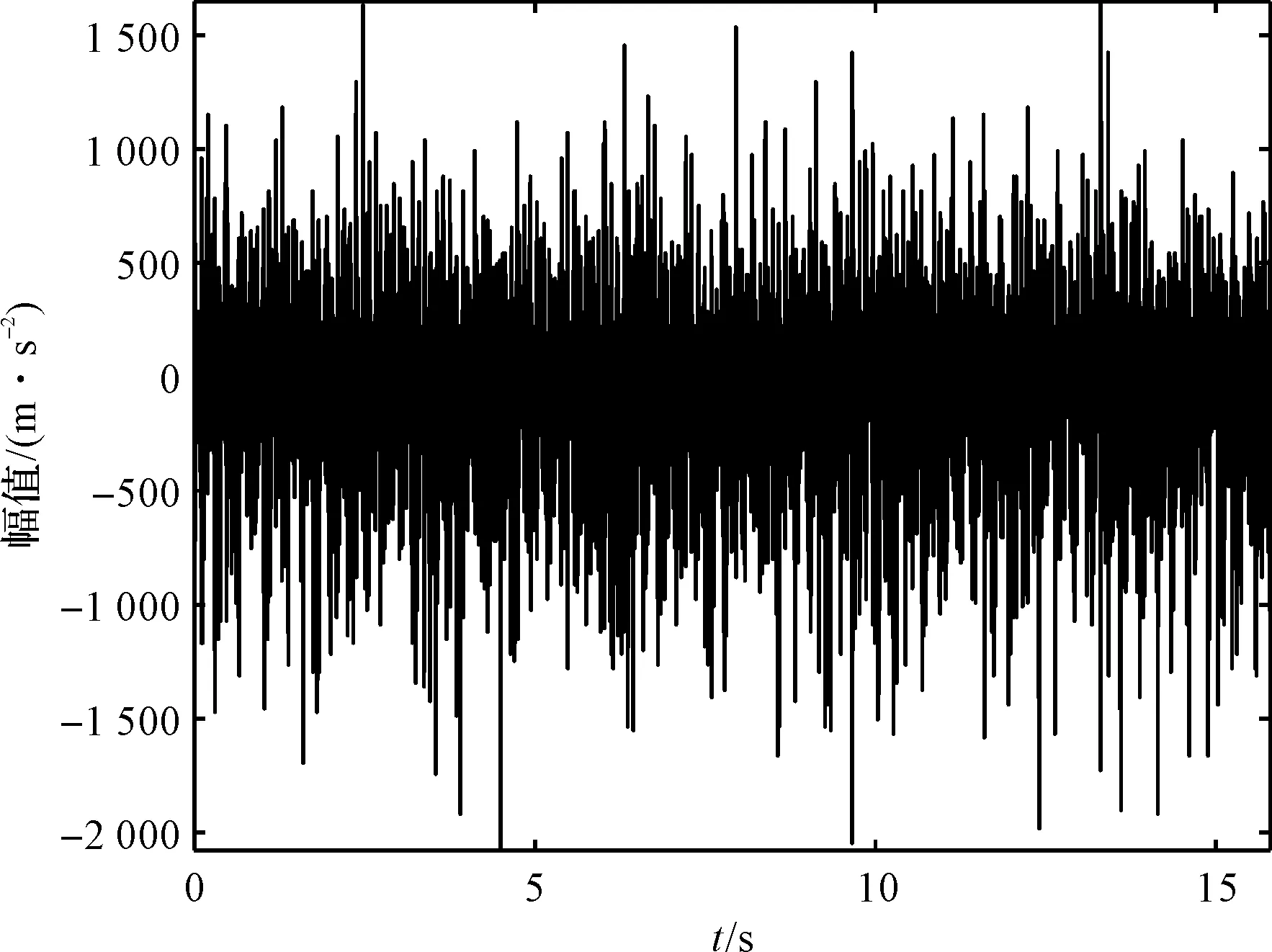
图9 正常信号时域图

实验获得实际信号中,磨损状态齿轮时域图如图10所示。

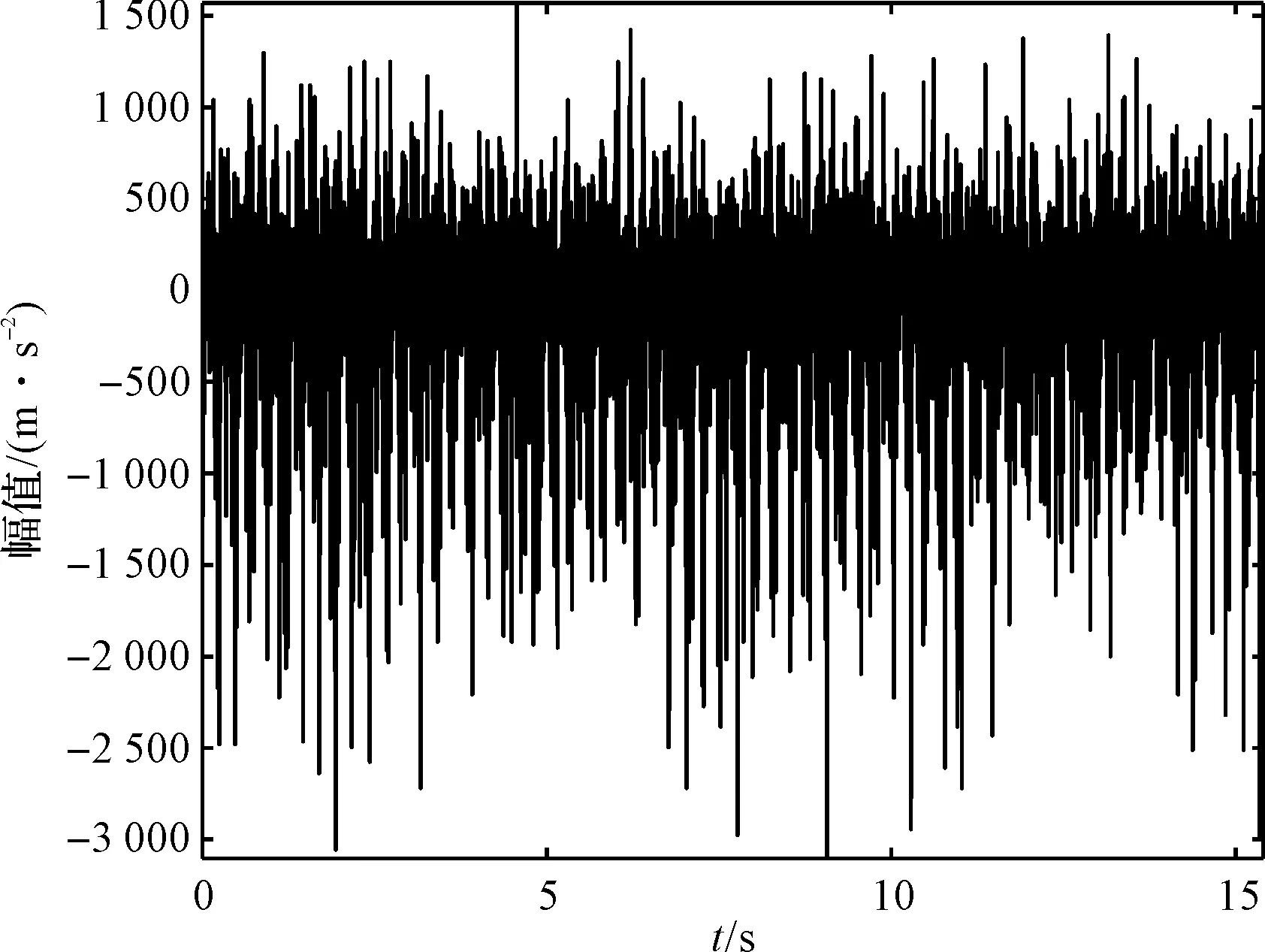
图10 磨损状态信号时域图

实验获得实际信号中,断齿状态齿轮时域图如图11所示。

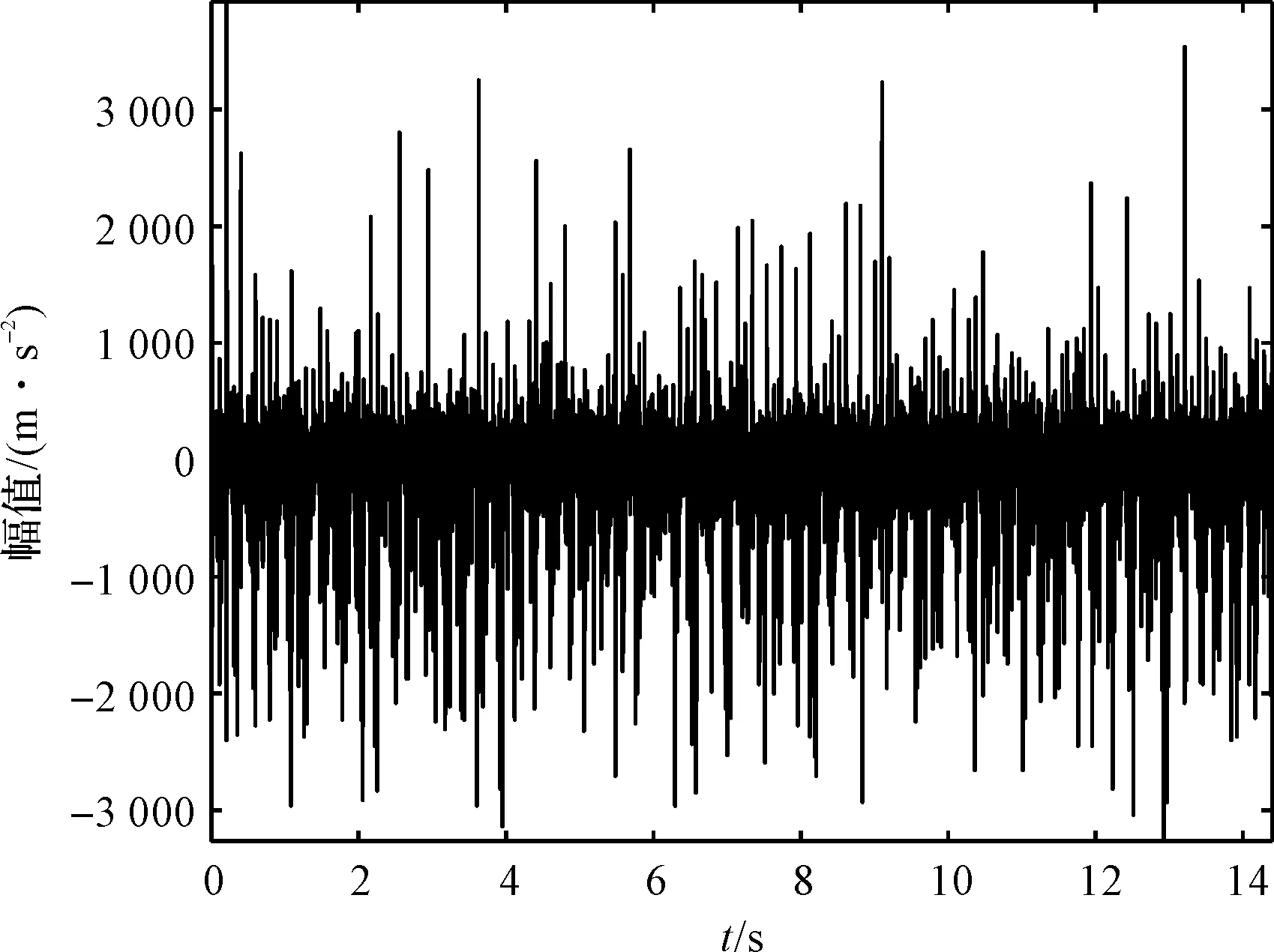
图11 断齿状态信号时域图

在正常状态、齿轮磨损、齿轮断齿3种不同故障模式下,笔者采用CSAEMD分解方法对其振动信号分别进行分解,并得到其分解结果的主要分量。

正常信号分解结果如图12所示。

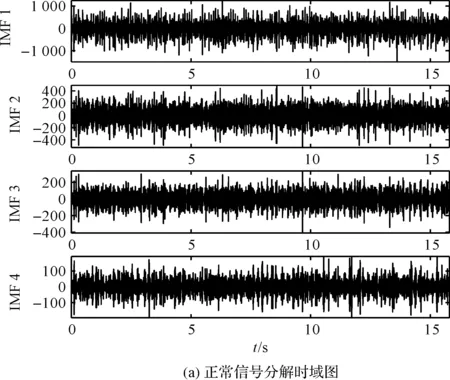
图12 正常信号分解结果

磨损信号分解结果如图13所示。

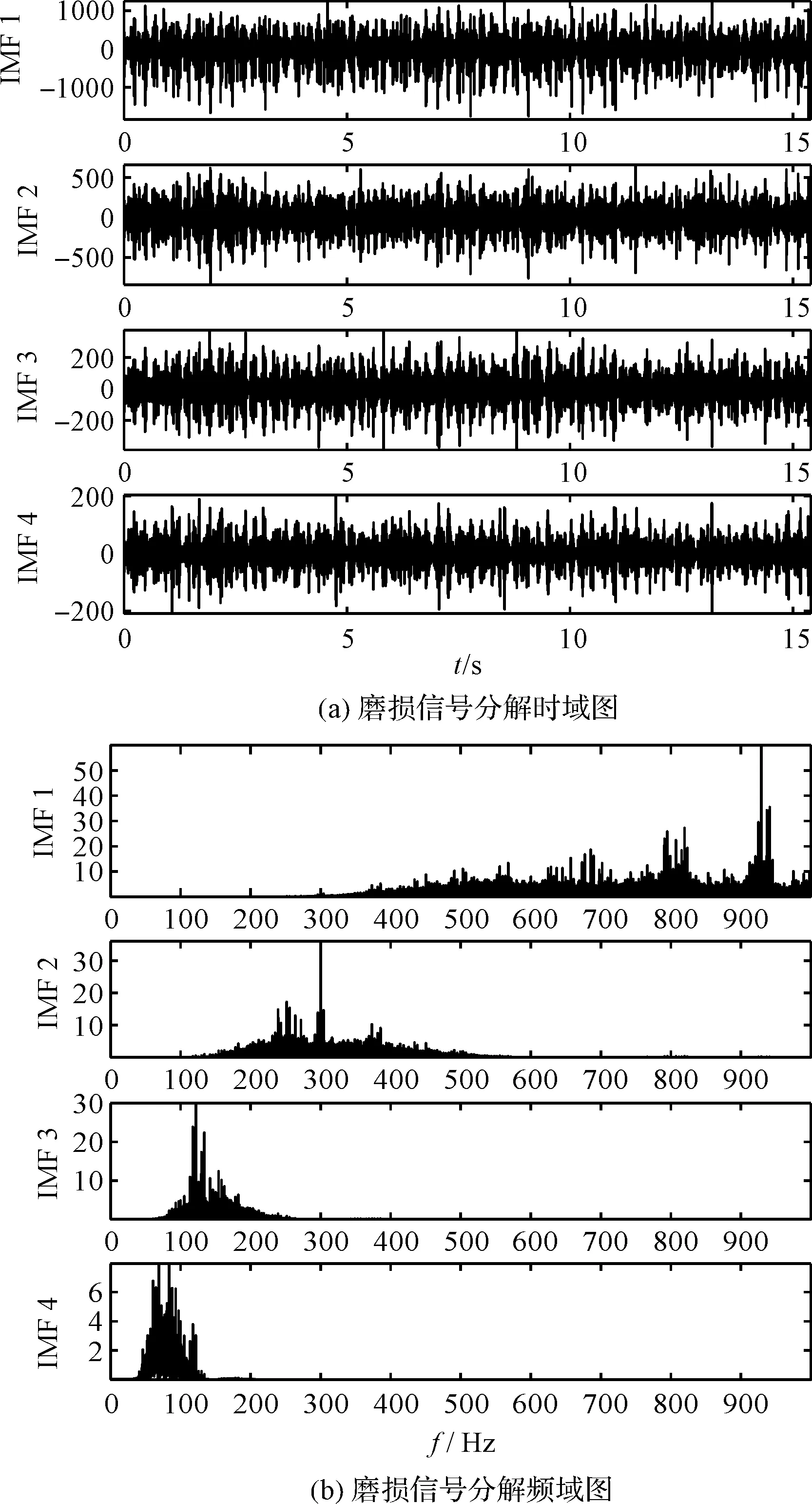
图13 磨损信号分解结果

断齿信号分解结果如图14所示。

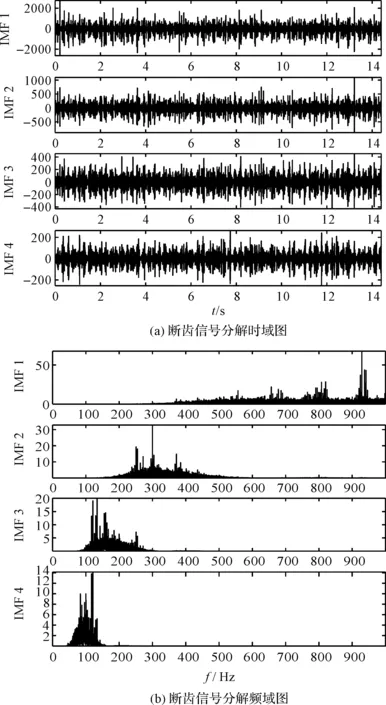
图14 断齿信号分解结果

3.2 核参数的选取

笔者使用CSAEMD对齿轮故障模式进行分解,并使用相关系数法,选择与原始相关最大的分量重构,再采用KECA对重构后的信号进行分析。

此处所采用的KECA中的核函数为高斯核函数,即:

(6)

式中:σ—高斯核函数的核参数。

核参数自适应选取的准则如下:

类内离散度为:

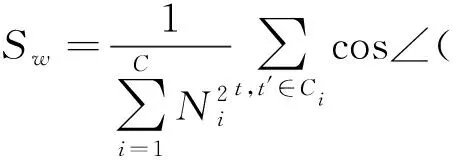
(7)

类间离散度为:

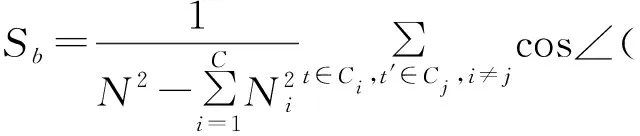
(8)

其中,Sw和Sb的取值范围为[0,1]。Sw表征同类样本基于角结构距离的相似程度;Sb表征不同类别样本间的相似程度。

在聚类分析中,目标是使类内离散度尽可能大,类间离散度尽可能小。因此,笔者采用基于角结构的类内和类间离散度的差作为选取的准则函数,即:

J=maxc,σ(Sw-Sb)

(9)

根据SHI J B和MALIK J[18]提出的核参数选取方法,首先要给出核参数选取区间(高斯核函数中的核参数通常取值为样本空间中欧式距离的中值的10%—20%),然后利用基于角结构的类内类间离散度的差为准则函数,自适应地选取合适的核参数。

此处,笔者选取正常状态、磨损、断齿3种齿轮故障模式各20个样本,进行聚类分析[19，20]。经计算,在经过CSAEMD分解重构后的样本空间中,欧式距离为4.004;因此,笔者选取核参数选择区间为[0.4,0.8];然后,利用基于角结构的类内类间离散度的差为准则函数,自适应地选取合适的核参数。

核参数的取值和准则函数值的对应关系如图15所示。

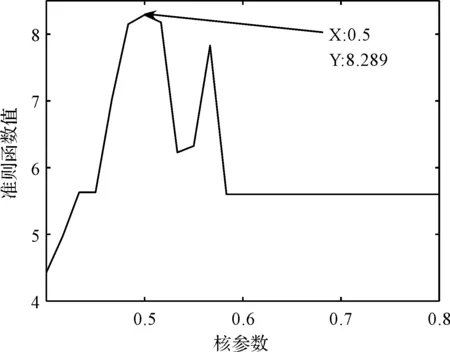
图15 不同核参数下的准则函数值

从图15可以看出:当核参数取值为0.5时,对应的准则函数值最大,为8.289。

因此,笔者选用0.5作为KECA中高斯核函数的核参数。

3.3 聚类分析

笔者运用样本间的cos值度量样本的相似性时,不同类别的数据间呈现明显的互成一定角度的特点(称为角结构特点)。在确定核参数和聚类数之后,采用KECA方法对数据进行分析,并引入KPCA进行对比(KPCA中核参数的选取方式及选取结果与KECA相同)。

经CSA-EMD分解重构后,齿轮故障数据(原始数据)的核矩阵如图16所示。

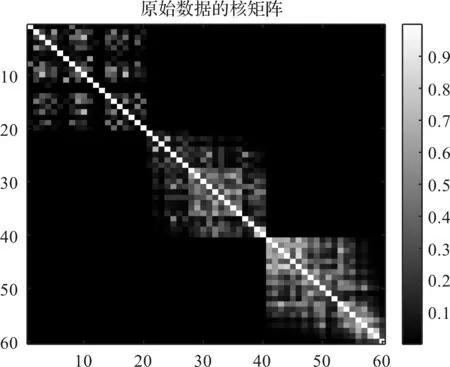
图16 原始数据的核矩阵

从图16可以看出:原始数据的核矩阵没有出现明显的分块结构。

为了进一步比较KPCA和KECA特征提取过程的性能差异,笔者利用选定最优核参数的KPCA和KECA,分别对原始数据进行特征提取,得到KPCA的核矩阵、KECA的核矩阵,如图17所示。

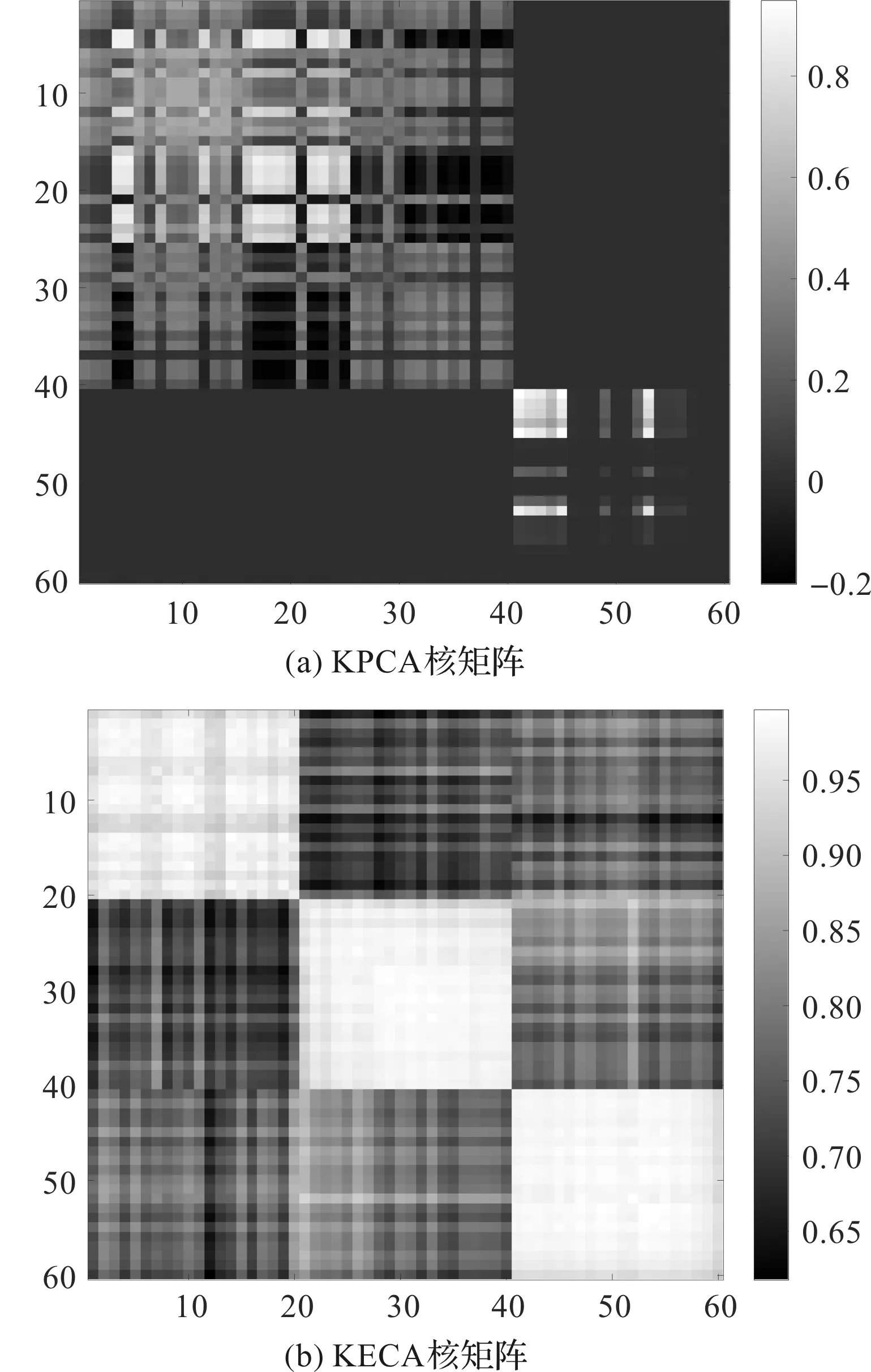
图17 不同方法下的核矩阵

从图17可以看出:KPCA的核矩阵没有出现明显的分块结构;

KECA的核矩阵出现一定的分块结构,这说明KECA的特征提取效果要优于KPCA。

为了评价KECA和KPCA选取特征向量的标准,笔者用KECA和KPCA分别对原始数据的核矩阵进行分解,得到的特征值和瑞丽熵值,如图18所示。

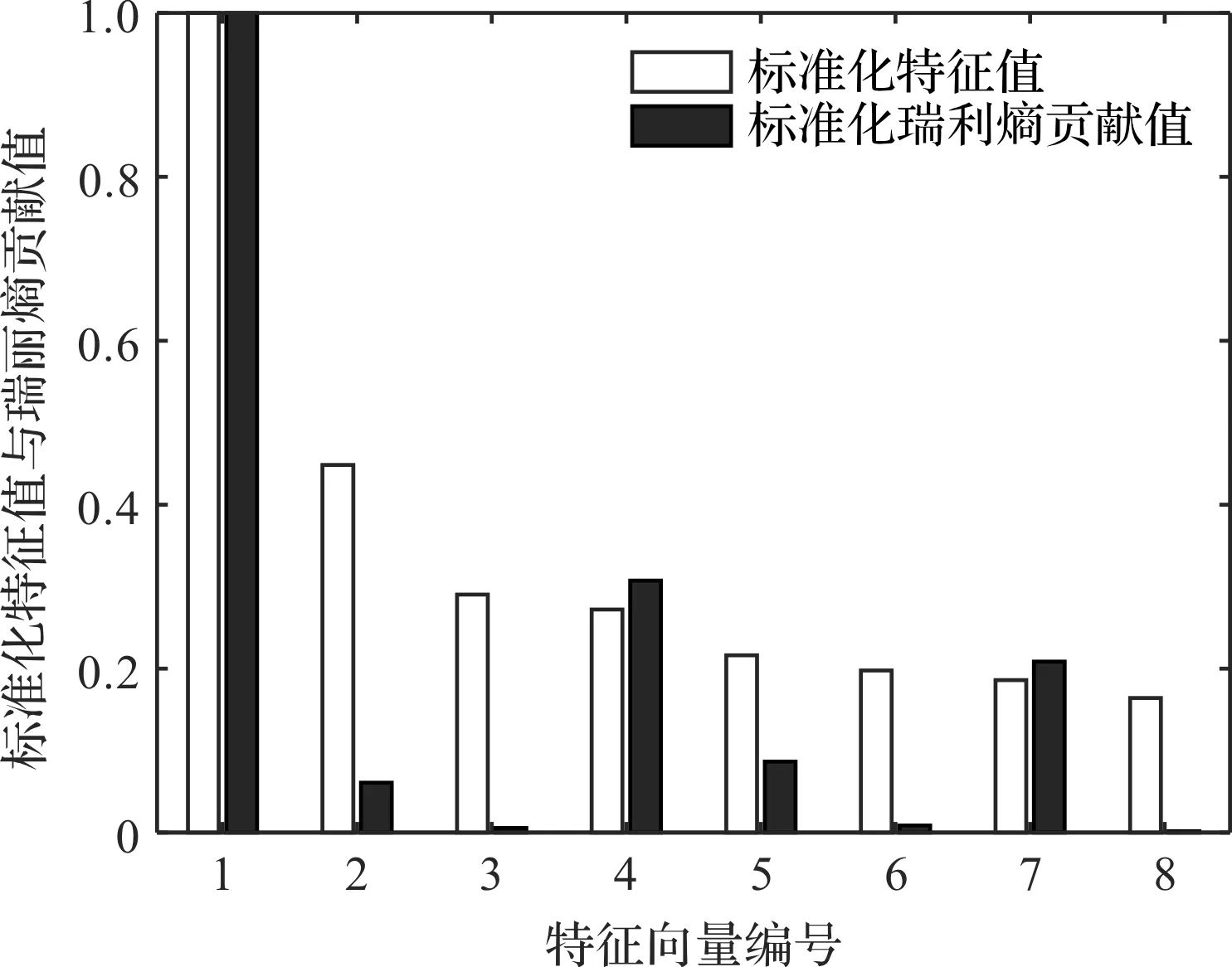
图18 标准化特征值与瑞丽熵贡献值

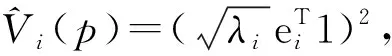
基于前3个最大特征值及其特征向量变换后的数据,以及基于前3个对瑞丽熵值贡献最大的特征值及其特征向量变换后的数据,笔者分别利用KPCA、KECA进行数据分析,得到采用不同方法选择的3个主成分,如图19所示。

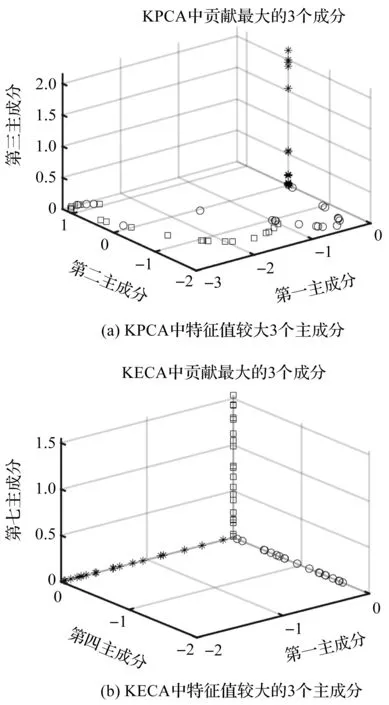
图19 不同方法选择的3个主成分

从图19可以看出:KPCA进行数据分析时,变换后的数据没有出现一定的角结构,这样会出现部分样本分类错误;

利用KECA进行数据分析时,变换后的数据在空间中基本上互相正交,具有明显的角结构特性。

从上述比较结果可以看出:在齿轮故障数据处理方面,相对于KPCA,KECA能够更有效地提取出齿轮故障数据的本质特性,利用角结构特性能够得到更好的聚类效果,从而实现对3种不同齿轮故障模式的聚类识别。

为了进一步说明不同算法的可靠性,笔者给出了PCA、KPCA、KECA的聚类结果。其中,PCA没有引入核方法,采用的是直接降维聚类;KPCA和KECA采用余弦矩阵进行聚类。

其聚类准则如下:通过两个方法进行特征提取后,不相似样本的特征向量在新的特征空间中是垂直的,而相似样本的特征向量是共线的,即不相似样本的余弦值为0,而相似样本的余弦值为1。因此,两个样本越相似,其余弦值就越接近1;两个样本越不相似,其余弦值就越接近0。

综上所述,样本间的余弦值可以作为聚类效果的度量。

采用不同方法得到的聚类结果如图20所示。

从图20可以看出:PCA用作齿轮故障模式聚类时,没有将相同的齿轮故障类别聚在一起,说明PCA的聚类结果不理想;

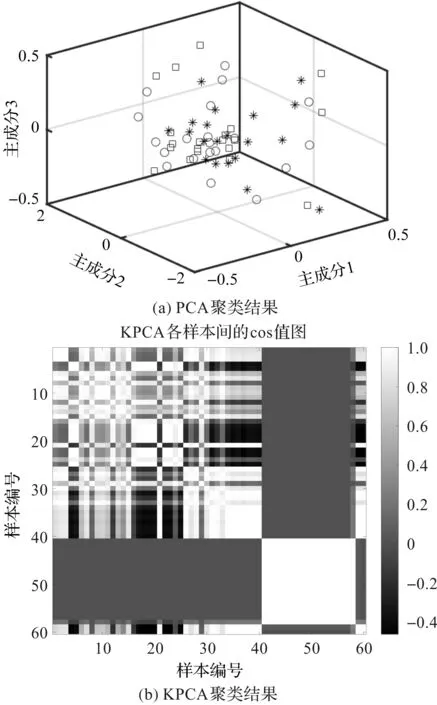
图20 不同方法聚类结果

当采用KPCA和KECA进行聚类分析时,cos值图的横纵坐标都表示样本编号,当聚类正确时,相同类别编号对应的cos值会无限接近于1,这时候,样本间的余弦矩阵就会呈现出明显的分块结构特点;

KPCA的余弦矩阵中第一、二类样本间没有明显块结构,第三类样本间出现较好的块结构特点,这表明KPCA仅实现第三类部分样本的聚类,聚类效果较差;

当采用KECA时,余弦矩阵具有明显的分块结构,实现三类样本的聚类。

实验结果表明,KECA在齿轮故障模式识别的聚类分析中具有良好的性能。

为了进一步说明KECA方法的有效性,笔者还计算了各个方法聚类的准确率。

采用不同聚类方法得到聚类的准确率如表1所示。

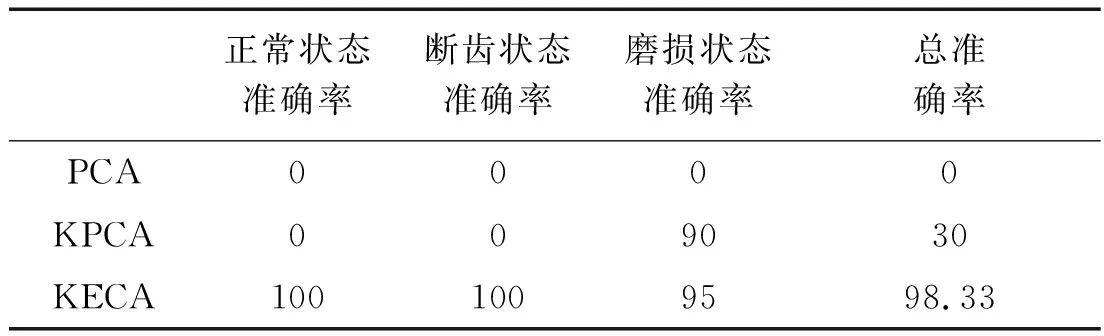
表1 不同聚类方法聚类准确率 (%)

从表1可以看出:PCA对于齿轮正常状态、齿轮磨损、齿轮断齿的聚类准确率都为0,聚类总准确率为0;KPCA对于齿轮正常状态、齿轮磨损、齿轮断齿的聚类准确率分别为0、0、90%,总准确率为30%;KECA对于齿轮正常状态、齿轮断齿、齿轮磨损的聚类准确率分别为100%、100%、95%,总准确率为98.33%。

以上计算结果表明:KECA方法在齿轮故障模式识别的聚类识别中的性能可靠。

综上所述,采用基于CSAEMD和KECA的方法,对齿轮故障进行模式识别是可靠的。

4 结束语

针对原始齿轮故障信号存在噪声分量,影响故障识别的问题,笔者提出了一种基于CSAEMD-KECA和角结构距离的齿轮故障识别方法。

首先,利用CSAEMD方法对原始齿轮故障信号进行分解重构,增强信号的鲁棒性,在去除信号中噪声分量的同时,尽可能地保留其原始特征信息;然后,利用KECA对重构后的信号进行特征提取,根据瑞丽熵贡献值的大小进行投影向量的选取,并构成新的数据集;最后,利用基于角结构距离的聚类方法进行聚类,实现对齿轮故障模式的聚类识别目的。

研究结论如下:

(1)利用CSAEMD方法对原始数据进行了分解重构,即在原始信号中加入与原始信号主要频率大约相等的正负正弦分量,减少了模式混合问题,使原始信号在去除噪声分量的同时,不会丢失重要的特征信息;

(2)利用基于KECA对CSAEMD分解重构后的齿轮故障信号进行了特征提取,选取了对样本瑞丽熵贡献值较大的3个特征向量作为投影向量,不同故障信号的投影向量互成一定的角结构。样本数据向投影向量投影，形成了特征数据集;

(3)利用基于角结构距离的聚类方法,对特征数据集进行了聚类分析,实现了对不同齿轮故障模式的聚类识别目的,聚类的准确率达到了98.3%。

在目前的研究中,仅是针对齿轮故障模式时域上的数据进行聚类分析,并没有考虑到频域数据所包含的特征信息,所以导致其所提取的特征不够全面。

在后续的研究中,笔者将考虑同时对预处理后的信号进行时域、频域、小波域上的特征提取,以进一步提高齿轮故障模式识别的准确率。