煤体裂隙非均质分布对注浆渗透扩散规律的影响分析

付中华

(山西省长治经坊煤业有限公司，山西 长治 046000)

煤炭在相当长时间内仍是我国能源结构的主要部分。在煤炭资源开采过程中，针对裂隙煤体(包括原生裂隙、采动裂隙等)的岩体稳定性控制是亟需解决的关键技术问题之一[1]。围岩支护技术不当将导致严重破坏事故[2]。裂隙煤体注浆是封堵裂隙及加固煤体的主要手段之—[3]，但是由于裂隙注浆属于无法直观监测的过程，煤矿井下难以获得煤岩中的浆液的注浆参数。现场注浆设计一般依据注浆规程，但注浆规程设计多来源于经验总结，滞后于现场需求，特别是针对破碎煤体的注浆设计规范不足，导致现场注浆设计大多凭经验设计，具有较大的盲目性，亟需完善注浆理论，指导设计注浆方案。

探明浆液渗透扩散规律是目前注浆理论研究中的一项重要内容，针对这一问题国内外学者已通过理论分析、实验室试验、数值模拟等方法开展了大量研究。在浆液扩散模型方面，如G.Lombardi[4]根据力的平衡，导出了裂隙注浆的扩散半径公式；阮文军[5]考虑粘度时变性推导了牛顿流体和宾汉流体的注浆扩散模型；郑玉辉[6]研究了牛顿流体和宾汉流体的注浆扩散模型在诸多影响因素下的变化规律；葛家良[7]建立了浆液在结构面中扩散的GJL模型。在裂隙岩体注浆数值计算及实验研究方面，杨米加[8，9]建立了裂隙网络下非牛顿流体渗流模型；刘健[10]研究了动水情况下浆液渗透扩散模型；李术才[11，12]等推导了C-S浆液在等开度单一平板裂隙中辐向扩散规律；王强[13]从微观角度研究浆液在裂隙中的流动；陆银龙[14]得出了微观角度下浆液与岩体黏结界面结构特征。

总体来讲，现有的煤体裂隙浆液渗透扩散研究成果中主要侧重于无限延伸单裂隙内流动的解析解和裂隙网络中的数值解，均属于理想的均质裂隙煤体模型。而实际工程中煤体内裂隙分布往往表现为复杂的空间非均匀分布形态，现有研究未能考虑这种裂隙非均匀分布对浆液渗透扩散规律的影响，因此迫切需要完善相关裂隙煤体注浆理论。

以山西经坊煤业3-边角091运输大巷巷道迎采送掘工程为背景，采用数字照相与数字图像处理技术精细识别煤体裂隙非均质特征，提出基于Weibull分布的裂隙非均质性表征模型，利用多物理场耦合软件COMSOL建立裂隙煤体注浆渗透扩散数值计算模型，探究不同煤体裂隙非均质特征参数下的浆液渗透扩散规律。与传统模型相比本研究模型更符合工程实际情况，为裂隙煤体注浆设计及裂隙煤体稳定性控制提供一定计算模拟依据。

1 裂隙煤柱注浆改性工程地质概况

1.1 工程地质概况

山西经坊煤业3-边角08工作面长1047～1166m，宽199.75～224.7m，平均埋深246m。3-边角08工作面煤层及顶底板岩层性质如图1所示，煤层厚度6.3m，属半亮型煤；直接顶为灰黑色砂质泥岩，厚1.2m；基本顶为浅灰色的细粒砂岩，厚度6.1m；直接底为灰黑色泥岩，厚度0.84m；基本底为灰色细粒砂岩，厚度3.85m。

图1 3-边角08工作面顶底板岩层性质

3-边角08工作面采用综采放顶煤采煤工艺，与相邻的3-边角09工作面间保留煤柱20m。3-边角091运输大巷巷道断面为矩形，宽5.2m，高3.1m，沿煤层底板掘进。由于矿井采掘接替紧张，导致3-边角091运输大巷巷道掘进与3-边角08工作面回采出现对穿现象，即“迎采送掘”。3-边角091运输大巷巷道原支护采用锚杆锚索联合支护技术，巷道矿压显现剧烈，煤柱破坏严重。

1.2 煤柱破坏情况

3-边角091运输大巷巷道属于综放强动压回采巷道，煤柱上的支承压力最大值可达5.6倍的原岩应力[15]，围岩结构与整体强度严重劣化与衰减，围岩二次应力影响区以及破裂损伤区的范围较大，巷道锚杆锚索对围岩锚固约束作用弱化[16]，巷道出现剧烈的顶板下沉、片帮、底臌等严重破坏现象，巷道维护困难。

进一步分析3-边角091运输大巷巷道煤柱表面裂隙分布特征，可以发现：巷道两帮煤体破碎，裂隙深入煤体，既存在开度较大、长度较长的主裂隙，也存在开度较小、长度较短，细密分布的次生裂隙；煤柱中裂隙具有复杂的空间非均匀分布特征。

2 煤体裂隙非均质性表征模型

2.1 基于Weibull分布的裂隙非均质性表征模型

煤体中原生与次生裂隙广布，从宏观上看是非连续介质，若将煤体视作连续多孔介质，则忽视了非均质性对研究结果产生的影响[17]。已有研究表明[18，19]，部分煤体物性参数的非均质特征可用Weibull分布描述。

以煤体裂隙率分布表征其非均质性，裂隙率定义为裂隙识别图像中面积S1与煤体单元面积S2之比，如图2所示。模型中煤体各单元具有不同的裂隙率，裂隙率数值大小的空间分布规律总体满足Weibull分布概率密度方程：

式中，φ为裂隙率；φ0为平均裂隙率；m为Weibull分布方程的裂隙率分布均质性指数。

图2 煤体单元裂隙率

2.2 煤体裂隙识别及非均质分布模型验证

由现场获得的煤体裂隙数字图像，采用数字图像处理技术可提取出图片中像素灰度值，进一步由阈值法可识别出煤体中裂隙，即利用图像像素灰度的强度差异(图像中灰度值较大的部分为裂隙)来提取裂隙的几何形态特征。3-边角091巷道帮部典型的裂隙数字图像识别如图3所示。由图3可知，图像处理结果与原裂隙相比形态一致，可识别出大裂隙与细小裂隙。

图3 3-边角091巷道帮部典型的裂隙数字图像识别

基于上述煤体裂隙识别结果与裂隙率定义，考虑将裂隙数字图像划分为50×50的像素单元，分别计算每一个单元中黑色部分(裂隙)的面积占比，即单元的裂隙率。基于图像识别的裂隙率分布统计结果与Weibull模型拟合结果对比结果如图4所示，可以发现拟合结果(平均裂隙率φ0=0.008、均质性指数m=8)与实际统计结果的相关性系数R2=0.95，表明Weibull模型能够较好地描述煤体裂隙非均质分布特征。

图4 基于图像识别的裂隙率分布统计结果与Weibull模型拟合结果对比

3 煤体裂隙非均质分布对注浆渗透扩散规律影响数值模拟

在对注浆过程的研究中，探究浆液在煤体中的渗透扩散规律是一项重要内容，传统研究将围岩视作连续均匀介质，忽视了煤体非均质性对浆液渗流扩散影响，对浆液扩散速度及浆液扩散距离等关键参数难以估计，造成计算的扩散范围与工程不符，导致设计参数不合理，进而注浆效果差。本节中基于前述提出的煤体裂隙非均质性表征模型，建立考虑裂隙非均质分布的煤体注浆数值模型，研究平均裂隙率及裂隙分布均质性指数对浆液渗透扩散规律的影响。

3.1 考虑裂隙非均质分布的煤体注浆数值模型

以经坊煤业3-边角091运输大巷巷道具体条件为背景，利用多物理场耦合软件COMSOL建立考虑裂隙率非均质性的二维平面浆液扩散数值计算模型(图5)。数值模型尺寸为5000mm×3100mm，注浆孔尺寸为42mm×1000mm。模型左边界为巷道表面，设定压边界浆液压力为0MPa；注浆孔深入煤柱内部注浆，模拟注浆实际情况，注浆孔作为浆液入口设为定压边界压力为3MPa，注浆时间为500s。注浆过程中设定监测线AB及监测点C，探究浆液渗透扩散规律。模型中浆液为普通水泥基浆液，水灰比1∶1，运动粘度为0.115Pa·s，浆液在煤体中渗透扩散控制方程[20]满足达西定律。

图5 煤柱注浆渗透扩散数值模型

浆液渗透扩散行为取决于模型中煤体的渗透系数，渗透系数与煤体裂隙分布几何特征参数密切相关(可假设满足修正立方定律)。根据前述煤体裂隙非均质表征模型，数值模型中裂隙率大小分布满足Weibull分布规律，每一单元的裂隙率通过Monte-Carlo随机模拟方法确定。

不同均质性指数下(m=1，5，10，∞；φ0=0.01)数值模型中裂隙率分布如图6所示。图中颜色的亮度表示裂隙率的大小，颜色越亮裂隙率越大，颜色越暗裂隙率越小。可以看出：当裂隙分布均质性指数为10时，相应的裂隙率分布图亮度要远大于裂隙分布均质性指数为1时的分布图。当裂隙分布均质性指数为1时，裂隙率的分布区间为0.003到0.015，而当裂隙分布均质性指数为10时，裂隙率的分布区间为0.008到0.012，可见裂隙分布均质性指数m越大，裂隙率分布区间更小，裂隙率更集中的分布在平均裂隙率φ0=0.01附近。

图6 不同裂隙分布均质性指数下裂隙率分布

为探究煤体裂隙分布非均质特性对浆液渗透扩散影响，建立两类数值计算模型：①研究不同平均裂隙率影响，取φ0=0.001、0.005、0.008、0.012；②研究不同裂隙分布均质性指数影响，取m=3、5、8、10。

3.2 平均裂隙率对浆液渗透扩散规律影响

不同煤体平均裂隙率(φ0=0.005、0.012)下浆液压力分布如图7所示，不同平均裂隙率下注浆结束时监测线AB上浆液压力分布曲线如图8所示，由图7、图8可知：不同平均裂隙率下，随距注浆孔距离增大浆液压力逐渐减小，且平均裂隙率越高，相同位置处浆液压力越大。根据浆液压力分布云图，可以确定不同时刻下浆液渗透扩散距离，本文定义浆液压力0.1MPa处为浆液锋面，沿AB方向其到钻孔距离即为当前时刻浆液渗透扩散距离。

图7 不同煤体平均裂隙率下浆液压力分布

图8 不同煤体平均裂隙率下监测线AB浆液压力分布

根据上述浆液渗透扩散距离定义，不同煤体平均裂隙率下浆液渗透扩散距离随注浆时间变化规律如图9所示，由图9可知：①不同平均裂隙率下浆液渗透扩散距离均随注浆时间逐渐增大，且注浆初始阶段(0～100s)浆液渗透扩散速率显著高于注浆中后期阶段(100～500)；②平均裂隙率越高，浆液渗透扩散速率越快，当平均裂隙率从φ0=0.001增大到0.012时，注浆初始阶段浆液渗透扩散平均速率从0.044cm/s增大至0.59cm/s，增大了13.4倍。

图9 不同煤体平均裂隙率下浆液渗透扩散距离随时间变化曲线

500s内浆液最大渗透扩散距离随平均裂隙率变化规律如图10所示，可以看出浆液最大渗透扩散距离随平均裂隙率变化且呈线性关系增长，当平均裂隙率从φ0=0.001增大到0.012时，浆液最大渗透扩散距离从0.16m增大至1.76m，增大了11倍。可见煤体平均裂隙率对浆液渗透扩散规律影响显著。

图10 最大浆液扩散距离(500s)随平均裂隙率变化规律

3.3 裂隙分布均质性指数对浆液渗透扩散规律影响

不同裂隙分布均质性指数(m=3，5，8，10)下浆液最大渗透扩散距离随注浆时间变化规律如图11所示，由图11可知：不同裂隙分布均质性指数下，浆液渗透扩散距离随时间变化特征相似，随着裂隙分布均质性指数增大，浆液渗透扩散距离有一定程度增大，当裂隙分布均质性指数从m=3增大到m=10时，浆液最大渗透扩散距离由1.14m增大至1.17m，增大了5.3%。

图11 不同裂隙分布均质性指数下浆液渗透扩散距离随时间变化曲线

监测点C在不同裂隙分布均质性指数下浆液压力大小随时间变化规律如图12所示，由图12可见：裂隙分布均质性指数越大，监测点C处浆液压力越大，当裂隙分布均质性指数从m=3增大到m=10时，C处浆液压力由0.28MPa增大至0.37MPa；当裂隙分布均质性指数达到一定程度后(m=8、10)，监测点C处压力同样为0.37MPa，因为此时模型中裂隙率分布趋近均匀，对结果影响较小。

图12 不同裂隙分布均质性指数下监测点C浆液压力随时间变化曲线

3.4 本文模型与传统模型对比

传统的浆液渗透扩散预测模型中未考虑裂隙非均匀分布特征的影响(属于理想的均质裂隙煤体模型)，故其模拟结果必然与实际存在较大差别。图13分别给出了本文模型(非均质模型)及传统模型计算得到的浆液压力分布云图(注浆时间为100s)，图14进一步给出了两种模型预测的浆液渗透扩散距离随时间变化曲线。由图13、图14可知：①传统模型中浆液锋面边缘光滑，压力分布均匀；而本文模型中浆液锋面边缘粗糙曲折，压力分布不均匀，与实际工程中浆液不均匀渗透扩散规律相符；②本文模型模拟的浆液渗透扩散距离相较传统模型模拟结果小16.9%，这是由于传统模型中未能考虑细小裂隙对浆液渗透扩散的影响，导致预测结果偏大，其应用于工程实际时将造成注浆材料、注浆参数等选取不合理，影响注浆工程质量。本文模型相比传统模型更符合工程实际情况，可为裂隙煤体注浆设计及裂隙煤体稳定性控制提供一定数值模拟依据。

图13 传统模型与本文模型预测的浆液压力分布云图对比

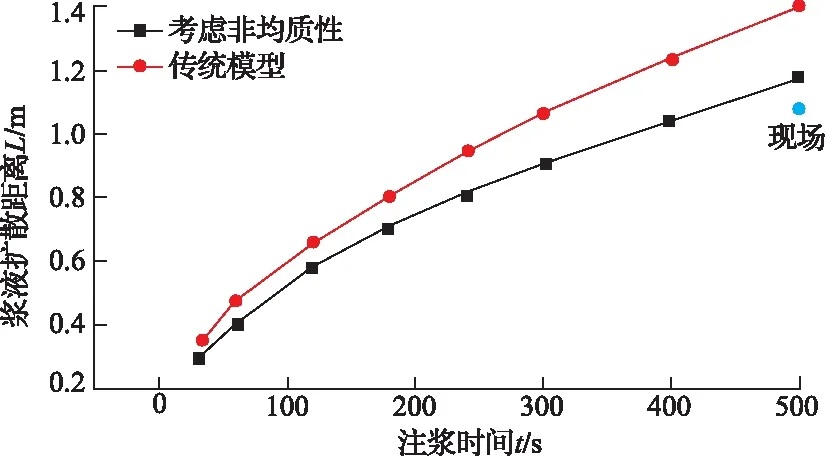
图14 传统模型与本文模型预测浆液渗透扩散距离对比

4 结 论

1)提出了基于数字照相与数字图像处理技术的煤体裂隙识别方法，建立了表征煤体裂隙非均质性的Weibull模型，结果表明Weibull模型能够较好地描述煤体裂隙非均质分布特征。

2)利用多物理场耦合软件COMSOL建立了考虑煤体裂隙非均质性的注浆渗透扩散数值计算模型，研究了平均裂隙率、裂隙分布均质性指数等因素对浆液在煤体裂隙中渗透扩散过程的影响。结果表明平均裂隙率越高，浆液渗透扩散速率越快，浆液最大渗透扩散距离越大，当平均裂隙率从0.001增大到0.012时，注浆初始阶段浆液渗透扩散平均速率从0.044cm/s增大至0.59cm/s，增大了13.4倍，相对应的浆液最大渗透扩散距离从0.16m增大至1.76m，增大了11倍；裂隙分布均质性指数越大时，浆液最大渗透扩散距离越大，当裂隙分布均质性指数从m=3增大到m=10时，浆液最大渗透扩散距离由1.14m增大至1.17m，增大了5.3%；煤岩中同一位置处浆液渗透扩散速率越快，浆液压力越大，但当裂隙分布均质性指数较大时，模型中裂隙率分布趋近均匀，对浆液渗透扩散结果影响较小。裂隙分布均质性指数越大，监测点C处浆液压力越大，当裂隙分布均质性指数从m=3增大到m=10时，C处浆液压力由0.28MPa增大至0.37MPa，增大了3.2%；当裂隙分布均质性指数达到一定程度后(m=8、10)，监测点C处压力同样为0.37MPa。

3)与传统模型(均质性模型)相比，本文模型(非均质模型)预测浆液锋面边缘粗糙曲折，压力分布不均匀，预测的浆液渗透扩散距离相较传统模型预测结果小16.9%，与实际工程中浆液不均匀渗透扩散规律相符，对于指导裂隙煤体注浆设计具有一定的参考意义。