基于蜜獾算法的破片序列图像多阈值分割

牛天利, 于丽霞，刘 吉,，武锦辉，牛雅昕

(1.中北大学 信息与通信工程学院，山西 太原 030051；2.中北大学 电子测试技术重点实验室，山西 太原 030051)

破片图像处理是静爆场破片参数测量的重要步骤之一，静爆之后的破片在运动过程中具有目标小、数量多和尺寸不一等特点，且在图像中还存在复杂的强火光背景和炸药未燃烧殆尽导致的运动破片灰度值相差较大等问题[1]。因此，在图像处理的过程中，将有效破片的运动区域和复杂的背景区域进行较高精度的划分有着重要的意义，图像分割是将其进行分离的重要步骤之一，分割的精度将直接影响到后期破片的检测和识别准确度。常用于图像分割破片目标的方法主要是基于一维灰度直方图的阈值门限法和改进的最大类间方差的方法等，但是这些方法更适用于具有单一目标、前景和背景灰度分布差别较大的破片图像中，而其余传统的图像分割方法，包括基于区域、图论、超像素和活动轮廓模型的方法，在实现过程中都存在时间复杂度较高的问题，实时性较差[2-4]。自卷积神经网络发展以来，基于深度学习的小目标分割也应运而生，但是基于深度学习的方法需要大量的数据集，并且在复杂的背景下算法的鲁棒性较差[5-7]。考虑到破片图像成像环境的复杂性和图像分割结果的特定应用场合，目前还没有普适的分割技术能够应用在处理这类图像中[8-9]。本文利用破片序列图像之间的相关性，采用帧差的方法对图像进行预处理后初步消除其背景[10-11]，采用蜜獾算法(Honey Badger Algorithm，HBA)优化的Tsallis相对熵多阈值图像分割算法对其进行较为精确的阈值分割。

1 HBA

1.1 基本原理

HBA是求解优化问题的新型元启发式算法之一。元启发式算法是在现实问题的复杂性和难度不断增加的过程中，为了适应不同的应用场合而不断发展的，具有灵活、无梯度机制、避免局部最优和计算成本低等优势[12-13]。

HBA是基于蜜獾的觅食行为发展而来的一种求解优化问题的高效搜索策略，是一种全局优化算法[14]。蜜獾的觅食行为可分为两种，一种是通过自身嗅和挖来寻找食物;另一种是通过跟随引导獾定位蜂巢。该算法将蜜獾的这两种行为分别设定为挖掘模式和采蜜模式，在算法实现中主要用于更新个体位置。HBA与大多数算法相同，都由探索和开发2个重要部分组成，探索将搜索范围扩展到搜索空间中较远的区域，开发是在搜索到的有效区域进行局部目标搜索[15-16]。探索和开发本质上是两种相互矛盾的功能，需要控制种群中的随机性确保两者功能的平衡[17-18]。HBA结构大体分为种群初始化、种群评估和更新参数3部分，其包括3个主要控制参数，分别为强度I、随机控制因子α和改变搜索方向的标志F。强度I用于调整由探索到开发过程以及避免局部最优。随机控制因子α在迭代过程中随时间衰减，减少种群的多样性，保证探索和开发阶段的平衡。改变搜索方向的标志F为给定的搜索空间的搜索提供种群的多样性。

1.2 算法的基本步骤

HBA的实现步骤如下。

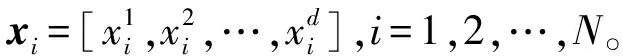
② 对种群大小和其位置进行初始化，xi=lbi+r1×(ubi-lbi)。r1为0～1之间的随机数；lbi和ubi分别为搜索空间的上边界和下边界；l和u分别为自定义数值范围的上界和下界；bi一般设为d维单位矩阵。

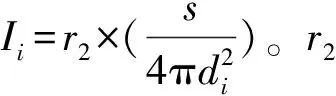
⑤ 跳出局部最优，使用标志F改变搜索方向，使得搜索个体严格扫描搜索空间，在实现过程中与步骤⑥相结合。

⑥ 更新个体位置xnew，分为挖掘阶段和采蜜阶段。在挖掘阶段，蜜獾的运动可用心脏线来表示，xnew=xprey+F×β×I×xprey+F×r3×α×di×|cos2πr4×[1-cos(2πr5)]|。xprey为目前全局最优位置；β≥1，表示蜜獾获取食物的能力，默认值为6；di为猎物与第i只蜜獾之间的距离，r3、r4、r5为0～1之间3个不同的随机数；F为改变搜索方向的标志，r6≤0.5 h时，F=1，其余时候F=-1；采蜜阶段是蜜獾根据蜂蜜向导寻找蜂蜜的情况，模拟为xnew=xprey+F×r7×α×di，在这个过程中蜜獾在猎物xprey附近搜索，搜索过程受密度因子α的影响。

2 Tsallis相对熵多阈值图像分割原理

Tsallis相对熵是在Tsallis熵和Kullback-Leibler散度的基础上提出的[19]，设两个离散有限概率向量A和B分别为A={a1,a2,…,an}和B={b1,b2,…,bn}，其中ai,bi≥0且a1+a2+…+an=b1+b2+…+bn=1，则Tsallis相对熵测度为

(1)

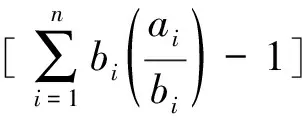
(2)

一维分布直方图情况下Tsallis相对熵的灰度级i对应的关于A1～AN+1的类概率为

(3)

式中：i=1,2,…,L；j=1,2,…,L；μj为分割后某一灰度级的类均值；σj为分割后某一灰度级的类方差。将分割后图像的灰度级用高斯模型进行拟合后表示为

(4)

式中：ri为对分割后图像高斯拟合后灰度级i在图像中出现的频率。将H和R对应的概率分布带入式(1)可得：

(5)

将式(5)作为图像多阈值分割的准则，由式(5)可知图像分割的最优阈值就是利用蜜獾算法取得式(5)最小值时对应的灰度值，则最佳分割阈值T由式(6)求得，使D(H|R)达到最小值时的灰度值的集合为

(6)

3 图像分割实验与分析

为了验证本文算法处理破片图像的精确性和有效性，需要将该方法与经典的阈值分割方法，例如Otsu法、最大熵法、最小交叉熵法对高速相机远距离拍摄的破片序列图像进行对比实验，对比其分割效果，之后利用遗传算法(Genetic Algorithm，GA)、蝗虫优化算法(Grasshopper Optimization Algorithm，GOA)和麻雀搜索算法(Sparrow Search Algorithm，SSA)与HBA进行Tsallis相对熵多阈值分割，验证HBA算法的优越性，其中任意选取的序列中的两帧图像如图1所示，在进行分割前需要对图像进行帧差反色预处理，帧差的目的在于将破片目标和运动背景进行粗略地分离。高速破片和复杂背景以不同的速度运动且利用高速相机在拍摄时帧率高、可拍摄到破片场局部变化等特点，选取两幅合适的间隔帧图像将相对应的灰度值相减，其复杂背景的运动速度比破片的运动速度小，帧差之后运动破片所在的区域与背景的差值会表现出较高的像素值，像素值越高，其运动趋势越明显，该像素位置的目标运动速度越快，而原背景运动速度较慢，帧差之后表现出较低的像素值。为了便于观察，对其进行反色处理，其结果由灰度值255减去当前值得到，反色后像素值越接近于0的部分表示该区域的破片运动速度越快，预处理结果图如图2所示。实验在MATLAB2018a上展开，Tsallis相对熵参数q设定为0.8。

图1 原始图像

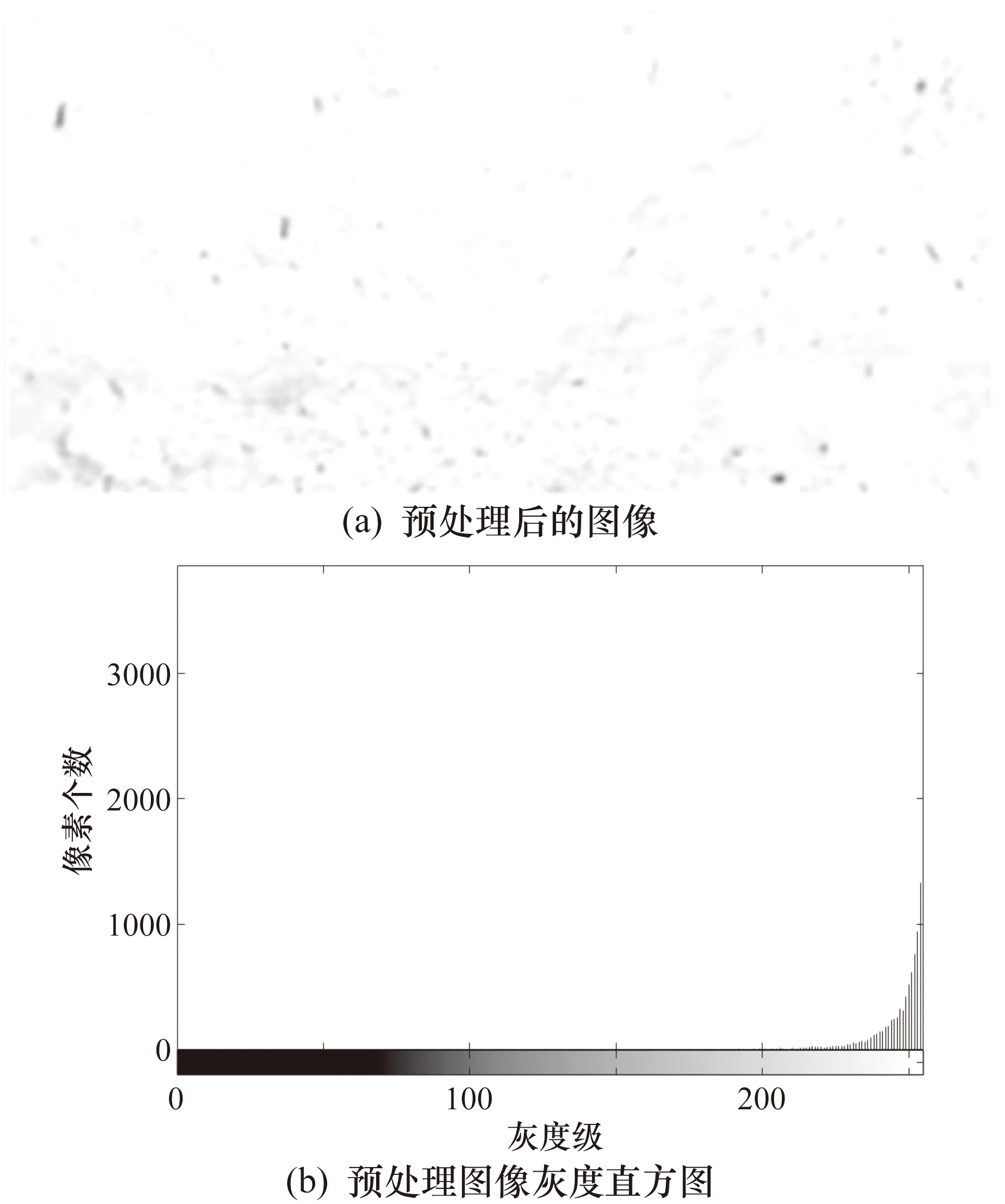
图2 预处理结果图

3.1 经典阈值分割法实验分析

利用上述的3种经典的阈值分割方法对预处理过的破片图像进行双阈值的分割，得到分割结果如图3所示。

在图像中灰度值越接近于0的部分表示其在实际运动中的速度越快，该部分是破片所在的像素点的可能性越大，因此分割出预处理后的图像中像素值最接近于0的部分至关重要。为了便于观察用JET映射的伪彩图对不同的灰度分布进行标记区分，其中蓝色部分表示分割后灰度值为0的部分，由图3可知，该方法能够将图像中破片所在的位置粗略分割，但是对于图像中左下角区域中较难分割的区域分割效果较差，为了清晰地观察到该区域的灰度分布，利用HBA的Tsallis相对熵多阈值图像分割对破片图像进行实验和分析。

图3 3种经典阈值分割结果图

3.2 HBA破片图像阈值分割实验与分析

3.2.1 阈值个数的选取

利用HBA对图2进行阈值分割，图像的灰度级为256，算法迭代次数为200，种群大小为40，分别选取阈值个数K=2、3、4，得到分割结果如图4所示。蓝色部分依然表示的是分割后灰度值为0的部分。分割结果表明，当K分别为2、3和4时，在左下角的局部区域总能观察到阈值分割后所需要的前景目标是不变的，K=2时的分割结果已经能明显看出所在目标，因此，后续对比分析的阈值个数K均取值为2。

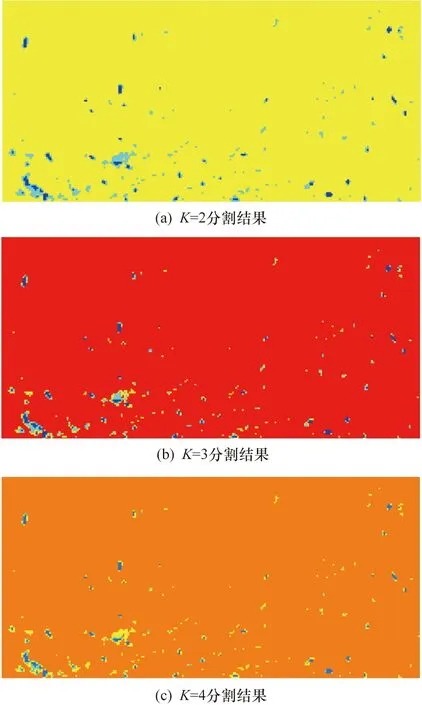
图4 基于HBA的多阈值分割图

3.2.2 GA、GOA、SSA与本文算法对比分析

在对破片图像的阈值分割过程中，为了比较HBA在阈值分割应用中的优越性，选取K=2，采用其余算法进行对比，其中GA、GOA和SSA分别代表遗传、蝗虫和麻雀搜索算法[23-25]，将其分别用于对破片图像进行Tsallis相对熵多阈值分割，选取每种算法迭代次数为200，种群大小为40，则得到GA、GOA和SSA的分割效果如图5所示。由图5可以看出，HBA的双阈值分割结果明显优于GA、GOA和SSA。

图5 GA、GOA和SSA双阈值分割图

为了对分割结果和算法性能进行客观描述，从阈值、熵值、实时性，以及算法的稳定性进行分析。根据Tsallis相对熵函数的式(3)可知，熵值越小，分割后的图像保留的信息越多。HBA收敛后得到的最小熵值即为最优熵值，求得最优熵值的阈值为最优阈值。算法的实时性也是检测该算法性能的重要性能指标之一，主要通过算法的运行时间来对比，运行所须的时间越短，其实时性越高[26]。算法的稳定性通常用算法多次计算结果的标准偏差(SD)衡量[27]，其公式为

(7)

式中：σi为第i次实验结束的Tsallis相对熵值；n为实验重复次数；μ为n次实验结果的均值，进行100次多阈值重复分割实验，验证算法的稳定性，标准偏差值越小，其算法的稳定性越高，4种方法的性能对比如表1所示。从表1可以看出，利用HBA进行图像分割后所得的阈值为5.14和254.17，5.14最接近0，可以更精确地分割出图像中灰度值接近0的像素点，将其作为单阈值分割的最终阈值；最优熵值3.56最小，相比于其他算法，HBA可以保留更多的信息；运行时间最短，在100次重复实验后求得标准偏差SD约为0，说明基于HBA的多阈值分割方法不但能有效分割出所须的前景目标，而且其实时性和算法的稳定性也最强。

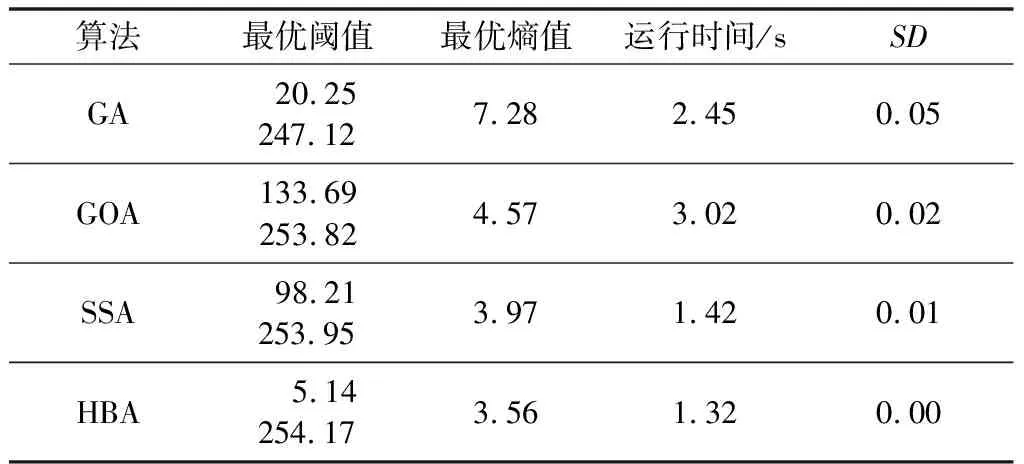
表1 4种方法的性能对比

4 图像分割结果验证

为了验证本文算法的有效性，首先,对高速相机拍摄到的破片序列图像进行帧差预处理，取帧间隔数为50;其次，利用本文算法对预处理过后的图像进行双阈值分割，选取双阈值中最小的阈值作为最终的分割阈值对图像进行分割处理，将分割出的目标作为破片识别的结果，并对其进行标记。由于破片目标较小，且形状不规则，因此，以破片目标的质心描述破片的全部信息。破片识别及质心标记结果如图6所示。

图6 破片识别及质心标记结果

根据高速破片运动轨迹的连续性和方向性，在已有的325幅序列图像中，分别对第1、51、101、151、201、251、301帧图像进行处理，检测到的破片个数如表2所示。

表2 检测到的破片个数

对多帧间识别到的破片目标进行轨迹拟合，每条轨迹的坐标数大于4为有效轨迹，根据轨迹的条数确定有效破片的数量，有效破片轨迹图如图7所示。

图7 有效破片轨迹图

图7中有26条连续的轨迹，即在所有识别到的破片中最终测得26个有效的破片。从表2中可以看出，每帧可识别到的破片平均约为31个，其识别率为

(8)

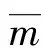
5 结束语

对破片图像的多阈值分割方法进行了研究，提出了基于HBA的Tsallis相对熵的多阈值分割方法，与经典的阈值分割方法相比，所提方法可以较准确地分割出图像中灰度值接近于0的部分，并通过对比GA、GOA、SSA的阈值、熵值、实时性和算法的稳定性等性能指标，说明HBA的性能优于其余3种算法。最后，根据分割出的目标绘制破片轨迹，确定有效破片的数量，结果表明，识别到的有效破片占总识别到的破片的83.8%，说明利用该阈值分割方法识别破片对视觉测试系统测量破片参数具有参考价值。