基于自适应采样时间MPC的自动紧急制动系统*

刘永涛，刘传攀，刘湘安，陈轶嵩，乔 洁

（1.长安大学汽车学院，西安 710064；2.中电科（宁波）海洋电子研究院有限公司，宁波 315000）

前言

根据统计数据，汽车碰撞在交通事故中占比高达70%，且大多数汽车碰撞事故都是追尾导致。其中驾驶人操作不当所导致的事故占比高达70%～90%［1］。自动紧急制动系统（AEB）作为重要的驾驶辅助系统，能够根据传感器检测到的环境风险信号自动执行相应的制动策略以辅助驾驶人制动，可以有效降低碰撞事故的发生，提高车辆行驶安全性［2］。

目前AEB 控制策略主要有基于安全距离和基于碰撞时间（TTC）两种。基于安全距离控制策略是发展最早也是发展较完善的一种控制策略，其核心是通过车辆制动时的运动学分析，结合驾驶人制动特性，通过运动学公式表达两车间的危险车间距并作为制动阈值。较为经典的安全距离模型［3-4］有Mazda模型、Honda模型、SeungwukMoon模型和Berkeley 模型等。以上模型均根据车间运动状态计算合适的制动减速度从而避免碰撞，但未考虑到驾驶人特性与舒适性。在此基础上，Francesco 等［5］利用驾驶模拟器进行驾驶人样本数据采集，并进行多元线性回归，建立了具有感知校准系统的安全距离模型，能够根据自车速度与相对速度大小进行自动调节；吕凯光等［6］通过对驾驶数据进行聚类分析，提出一种基于不同驾驶人驾驶风格的安全距离模型，在满足不同驾驶风格驾驶人个性化需求的同时提高了舒适性；Lee 等［7］则进一步研究了制动执行机构延迟对安全停车距离精度的影响并建立了相应的安全距离模型。此外，谈东奎等［8］在考虑预期功能安全的前提下，构建了自动紧急制动感知盲区安全距离模型，提高了车辆安全通过盲区的形式效率。

TTC 控制策略则根据两车相对运动状态，判断两车碰撞风险程度并进行相应制动，该策略以时间尺度衡量碰撞风险，更能体现驾驶人对于碰撞风险的观感与判断［9］。在此基础上，文献［10］中提出了一种基于自车与前车相对加速度的2 阶TTC 模型，解决了TTC 无穷大时系统无解的情况；裴晓飞等［11］采用碰撞时间的倒数作为评价指标，设计了基于危险系数的分级报警与主动制动的安全距离模型；兰凤崇等［12］利用分层控制提出了基于TTC的自动紧急制动系统分层控制策略；郭祥靖等［13］通过仿真手段构建紧急制动数据集，提出了一种基于BP网络预测TTC 预警时间和碰撞时间阈值的风险评估模型，提高了紧急制动时的安全性、舒适性和横摆稳定性。

目前学者们的研究大多注重于AEB 系统的安全性，对于驾乘舒适性讨论较少。Kyongsu等［14］较早提出考虑舒适性的制动控制策略，结合制动控制对车辆响应的影响与制动减速度突变对舒适性的影响，设计了能够减小制动冲击的加速度曲线，提高驾乘舒适性；黄城等［15］通过设置制动减速度变化缓冲区对制动减速度及其变化率进行限制，得到了满足舒适性条件的减速度控制曲线；Mahdi 等［16］则在利用轨迹规划进行车辆避撞研究时，将减速度与减速度变化率作为舒适性指标引入速度规划算法中，得到满足舒适性标准的加速度曲线，实现以平稳速度进行主动避撞。

上述研究主要聚焦于构建舒适的加速度曲线，但在实际运用过程中往往无法做到较好跟随效果，为能够将安全性与舒适性目标同时纳入到AEB 系统的决策过程中，本文中引入基于模糊规则的MPC算法，基于分层理论重新设计了AEB 系统，上层控制器根据车间状态信息与控制目标及约束条件计算出期望加速度值并传递给下层控制器，下层控制器通过期望加速度向车辆的制动系统发出控制指令，最后通过仿真试验与实车试验验证了控制器的效能并分析了试验结果。

1 基于MPC的AEB上层控制系统

1.1 车间动力学模型

上层控制器的任务主要是通过车辆采集到的前方车辆行驶信息与本车状态信息，对两车未来车间行驶状态进行预测并实时修正输出的期望加速度，因此建立的运动学模型只须能反映出两车的车间纵向运动学特性即可，故对模型作一定简化。在考虑安全性与乘坐舒适性的前提下，兼顾本车的加速度和加速度变化率，并将前车的加速度作为MPC 控制系统的扰动输入，建立车间纵向动力学模型，如图1所示。

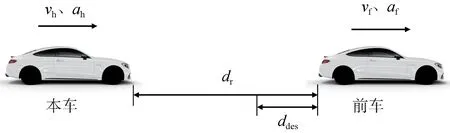
图1 车间纵向动力学模型

图中vh、ah，vf、af分别表示本车与前车的速度和加速度。根据两车的运动状态，可以建立本车与前车的状态关系模型为

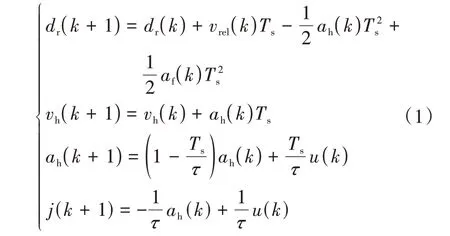
式中：dr为实际车间距；vrel为两车相对速度；Ts为系统采样时间；τ为描述本车期望加速度u与实际加速度ah的传递特性的1 阶惯性环节时间常数，一般取τ=0.53［17-18］；j为本车的加速度变化率。

1.2 基于模型的离散状态空间方程

将系统的状态变量定义为x(k)，选取上述4 项变量为系统的状态量，则

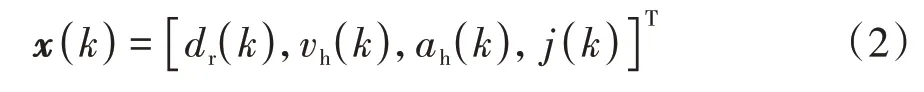
将前车加速度φ(k)作为状态方程的扰动量，以此提高状态方程的准确度与可靠性。由于控制目标是将车速降至0 并使最终车间距控制在安全距离内，所以将dr(k)、vh(k)作为系统的输出，由此可得系统的离散状态空间表达式为

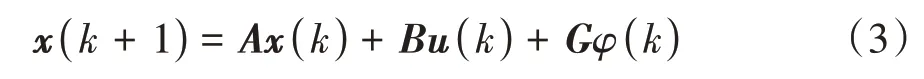
式中A、B、G均为系统的系数矩阵，结合式（1）、式（2）可得

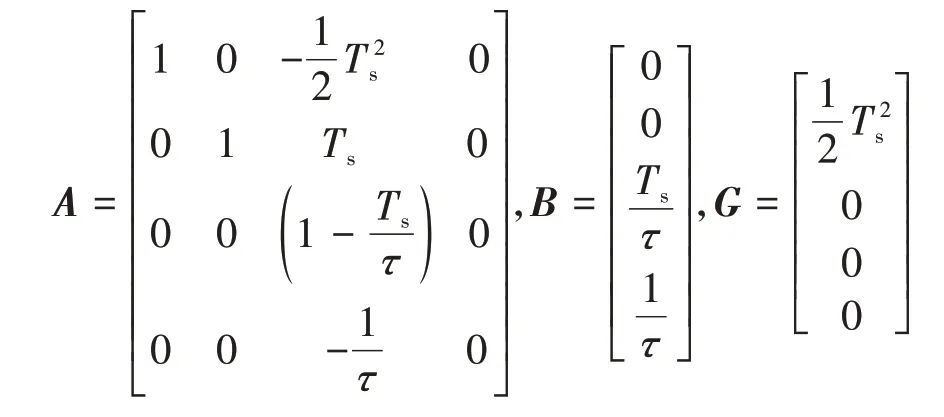
式（3）所表达的状态空间方程在考虑车间安全距离、车速、本车加速度、加速度变化率的前提下，将前车的加速度φ(k)作为系统的干扰量，使模型更加贴近于实际车间运动学关系。

1.3 AEB系统多目标控制性能要求与约束条件

为保证安全制动的前提下同时兼顾舒适性，定义车间约束条件为

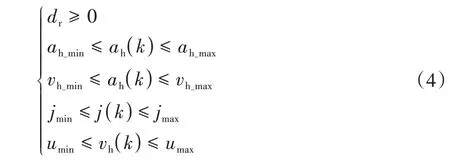
式中：vh-min、vh-max、ah-min、ah-max、jmin、jmax分别表示本车速度、加速度与加速度变化率的最小值与最大值；umin、umax表示期望加速度的最小值与最大值。

为尽快制动，应保证车辆速度能够降为0，并与前车保持安全的车间距，将优化目标表述如下：

式中ddes通常包含1 到2 个车身的距离，在自适应巡航系统中往往取一个车身的距离，考虑到自动紧急制动系统策略较为激进，故此处取0.8 个车身的长度。

选取车间距dr(k)，与本车车速vh(k)，本车加速度ah(k)及加速度变化率j(k)作为系统的输出变量，即

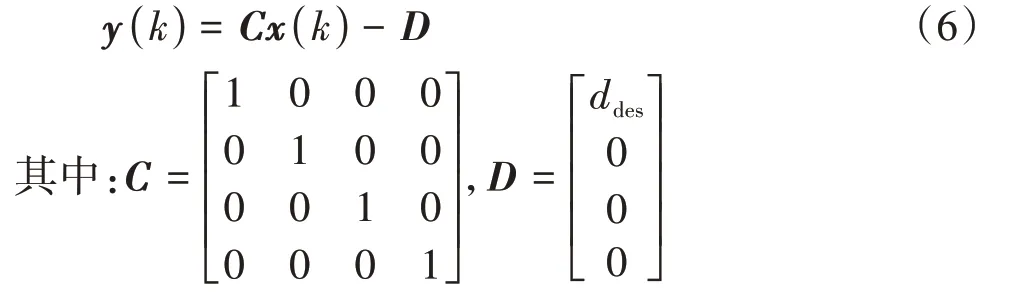
1.4 MPC控制器求解

根据式（3）和式（6）可建立如下模型：

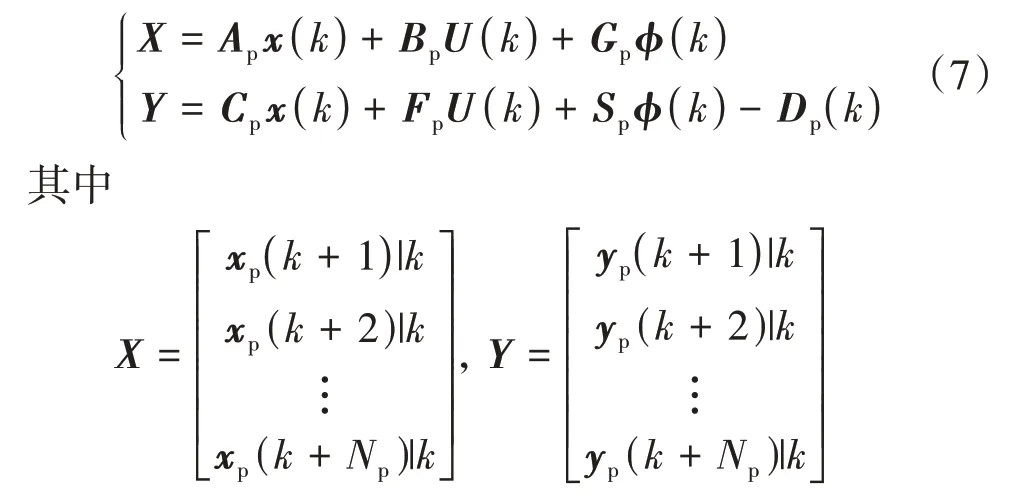
在设计MPC 控制器时，预测步长Np必须大于控制步长Nc，在控制时域内，能够得到相应的控制量对系统状态进行预测，而超出控制时域范围内的预测则假定控制量不再发生改变，可用式（8）进行描述：

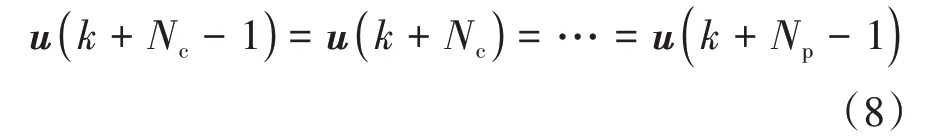
同时，为得到系统状态预测方程，认为前车加速度在预测步长内不发生变化，即

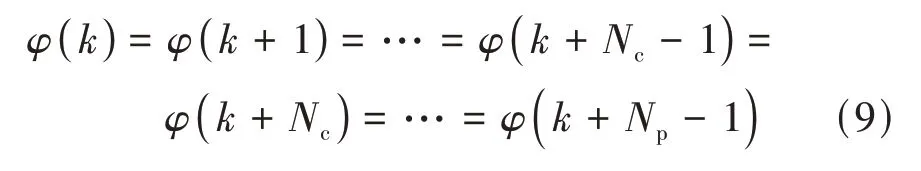
式（7）中的系数矩阵满足如下关系：

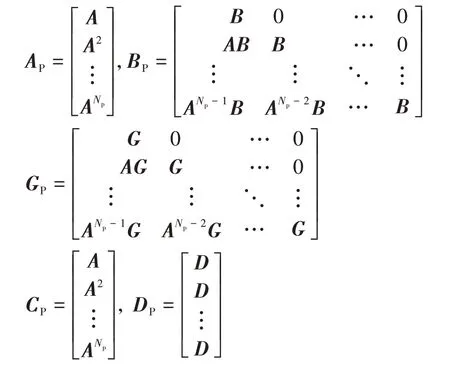
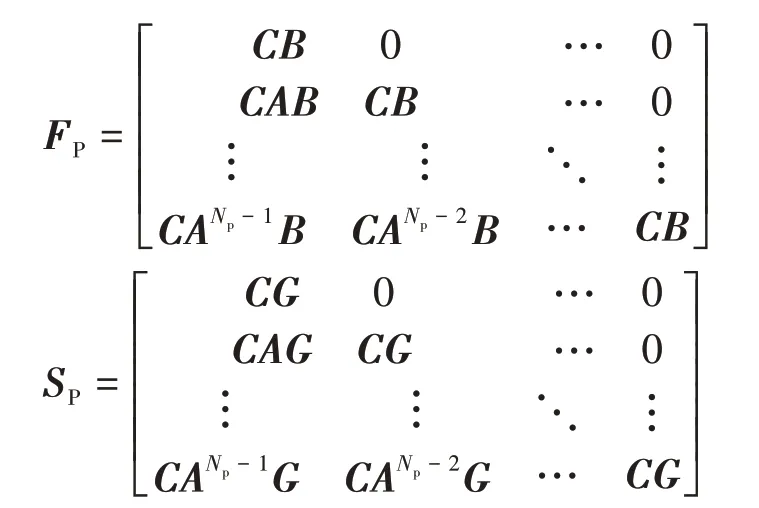
综合1.3节中对AEB 系统多目标控制性能要求的分析，将优化目标的评价函数定义为

式中：U为控制量；Q、R为权重矩阵，Q=中每个子矩阵代表每个状态量的权重因子，其值越大代表系统越趋向于减小其对应的状态量与参考量之间偏差；R=diag(qu)，R越大则代表系统更倾向于使控制量尽可能小。为防止系统无解，引入松弛系数ρ与松弛因子ε。

令E=Apx(k) +Gpφ(k)并将式（7）代入式（10）可得

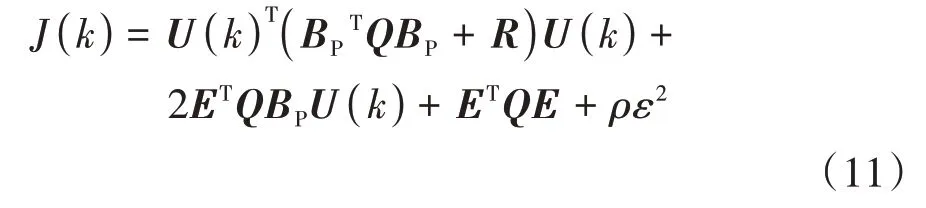
忽略式（11）中与控制量无关的项，并改写成如下形式：

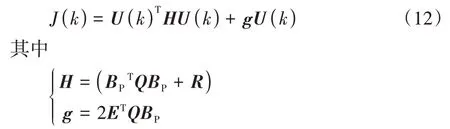
本文通过Matlab 优化工具箱中的quadprog 函数来求解式（12）这一标准二次规划问题，计算得到最优的上层控制序列U(k)，即每个采样时刻对应控制时域内的一系列最优控制量：

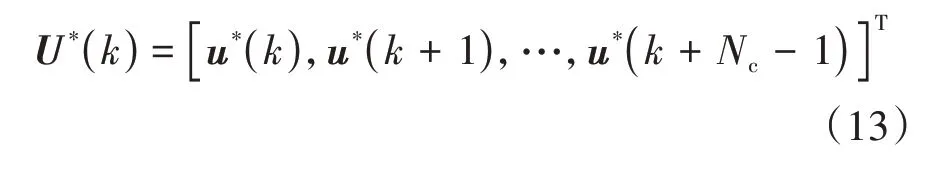
2 基于模糊规则的MPC控制器优化

MPC 控制器的控制精度与采样时间有关，但过小的采样时间会导致冗余制动和较高的计算成本，在紧急制动过程中，随着危险程度的变化，采样时间的自适应变化将会提高AEB 在不同场景下的适用性。通过模糊控制方法可以较好地描述二者之间的非线性关系［19］，为表征车辆自动紧急制动过程中的危险程度进而对MPC 控制器性能进行优化，本文中引入紧急系数i来衡量车辆行驶过程中的紧急程度。该系数为［0，5］的无量纲数，i从0到5代表紧急程度从最低到最高。此外，将AEB 中2 个重要参数作为输入，即相对距离和TTC。

2.1 隶属度函数与模糊规则确立

本文将相对距离模糊集合设定为｛极小，小，中，大，极大｝；TTC模糊集合设定为｛极小，小，中，大，极大｝，相应的逻辑语言均设定为｛NB，NS，ZO，PS，PB｝。根据仿真工况，将相对距离论域设定为［0，100］m，由于GB/T39901—2021《乘用车自动紧急制动系统（AEBS）性能要求及试验方法》中要求紧急制动不应在TTC=3 s 前开始，故将TTC论域设定为［0，3］。同样，将紧急系数i模糊化为｛极小，小，中，大，极大｝，相应的逻辑语言为｛NB，NS，ZO，PS，PB｝。输入变量和输出变量采用三角形隶属度函数，函数如图2所示。

图2 隶属度函数

模糊规则采用IF-THEN 结构，具体模糊规则如表1 所示。相对距离、TTC最大时，取最小紧急系数；相对距离、TTC最小时，取最大紧急系数。如果相对距离处于极大状态，则无论TTC如何变化，都认为两车处于安全状态，紧急系数i处于NB（极小）或NS（小）论域。如果相对距离处于极小状态，则无论TTC如何变化，都认为两车处于危险状态，紧急系数i处于PB（极小）或PS（小）论域。

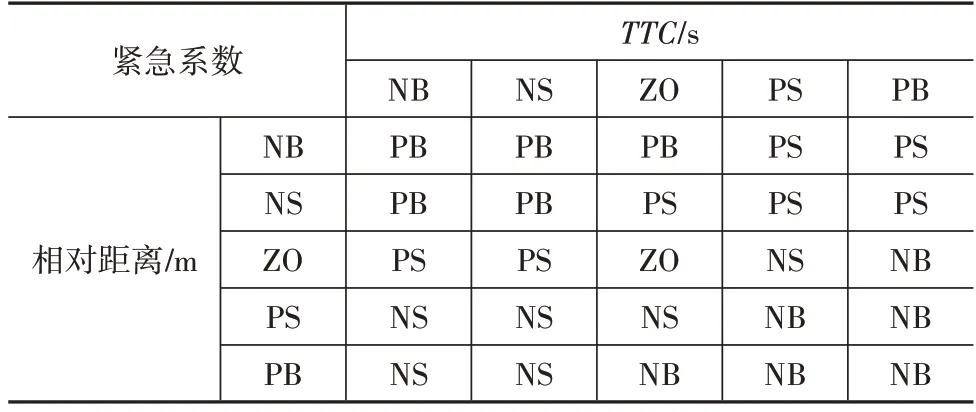
表1 模糊规则

通过Manadani 极大极小方法进行逻辑推理，并选用质心法解模糊化，求解得到的紧急系数曲面如图3所示。

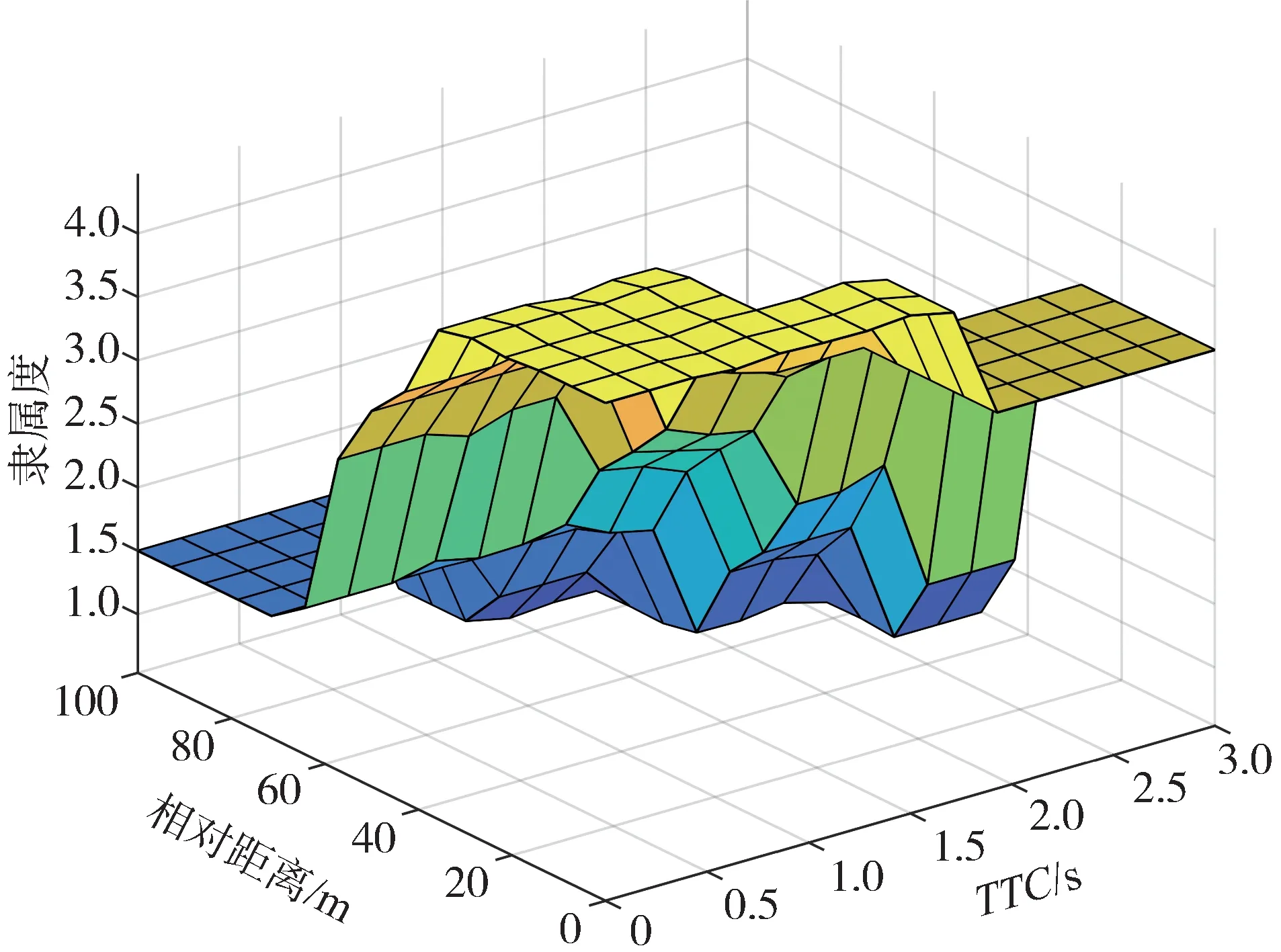
图3 紧急系数曲面

2.2 MPC控制器的优化

为降低在紧急制动过程中MPC 控制器的计算成本，同时应对更加复杂多样的场景工况，本文中提出了一种基于模糊控制的改进MPC 控制器，用于降低计算量，提高MPC控制性能。

MPC的控制性能主要取决于预测模型的精准度和控制参数。一般控制参数包括采样时间Ts、控制步长Nc和预测步长NP。随着采样时间降低，采样密度增加，MPC控制器的快速响应能力提升，但稳定性有所下降。因此，在场景紧急系数较低时，采用较大的采样时间，减少计算量，提高控制系统稳定性与乘坐舒适性；在场景紧急系数较高时，采用较小的采样时间，提高AEB 系统的响应能力，确保安全性，通过紧急系数来修正MPC 的采样时间，使控制器的效率大大提高。依据文献［20］，本文中将MPC 控制器的采样时间定义为

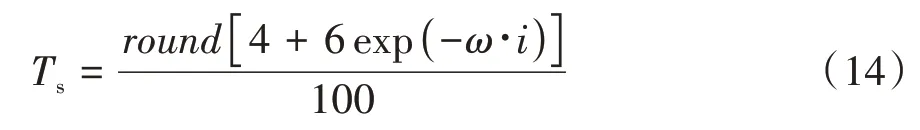
式中：round为取整函数；ω为收缩因子。通过式（14）可将采样时间限制在Ts∈[0.05 s，0.1 s]内，通过改变ω可调整采样周期的收敛速度。考虑到行车的安全性和舒适性，本文将ω设置为1。综合采样时间与紧急系数的关系，当Ts≥0.1 s 时，认为车辆处于较为安全状态，MPC控制器不介入系统。

3 车辆模型与下层控制器

3.1 基于PreScan的2-D汽车动力学模型

在进行车辆基本参数设置时，选取PreScan对象库中的Toyota_Prius 作为试验对象，其基本参数如表2所示。

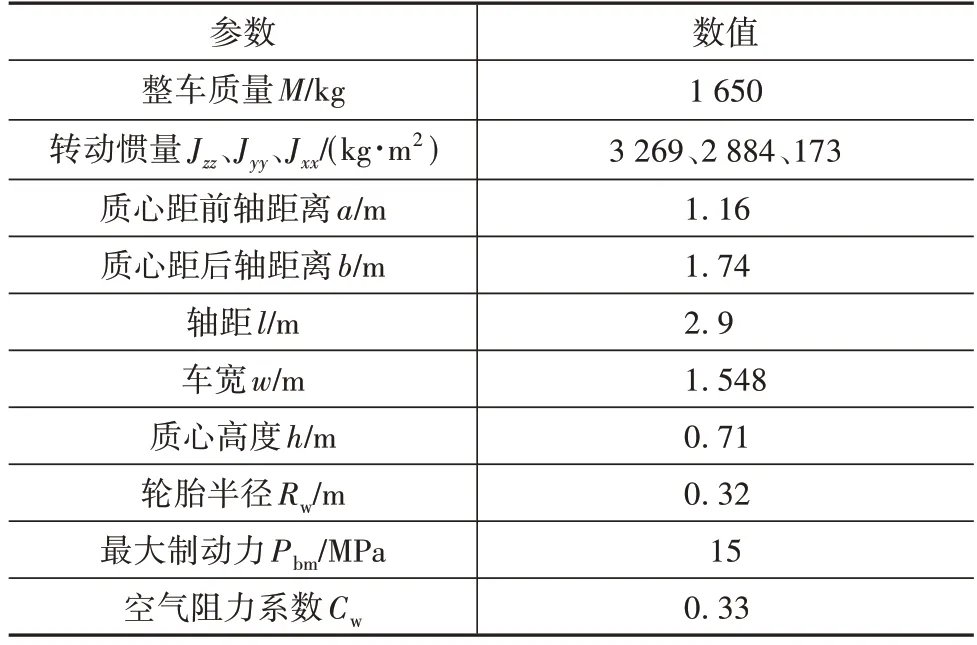
表2 Toyota_Prius车辆参数配置

3.2 下层控制器

下层控制器的主要功能是对上述车辆动力学模型进行控制，由于汽车纵向动力学的非线性特性［21］，车辆的实际加速度与期望值存在误差，采用PID 控制策略对加速度误差进行控制，将上层MPC 控制器输出的期望加速度与实际加速度差值作为控制误差e(t)，即

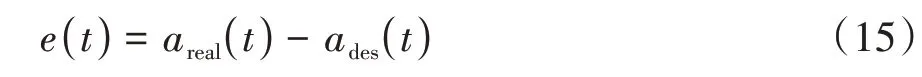
式中：areal(t)为实际加速度；ades(t)为期望加速度。

根据PID控制规律则有：

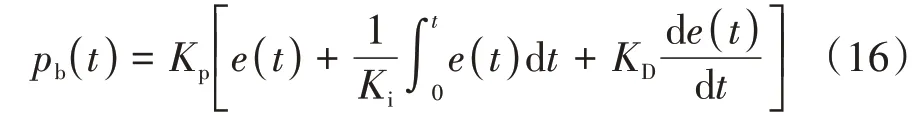
式中：Kp、Ki、KD分别为PID 控制器的比例增益、积分时间常数和微分时间常数；pb(t)为输出的制动压力值，在Simulink中构建下层控制模块如图4所示。

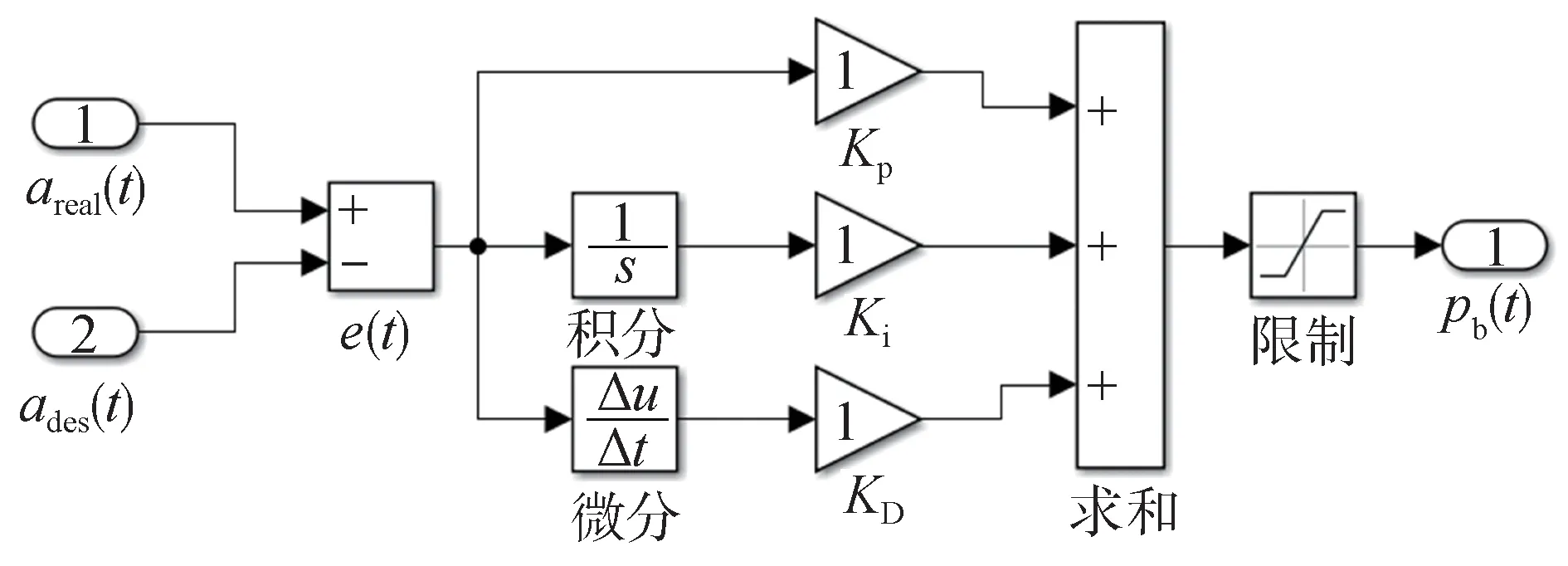
图4 下层PID控制模块

3.3 节气门开度控制模型

由于在AEB 系统中没有加速需求，因此节气门只须维持匀速行驶状态即可，将汽车行驶方程式展开可得

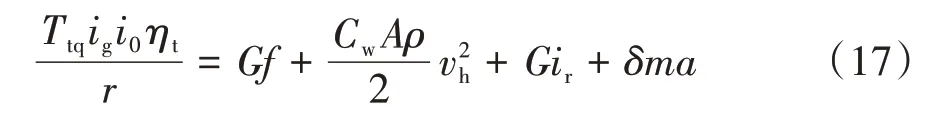
式中：Ttq为发动机输出转矩；ig、i0分别为变速器与主减速器传动比；ηt为传动系机械效率；r为等效车轮半径；G为车辆重力；f为滚动阻力系数；Cw为空气阻力系数；A为车辆迎风面积；ρ为空气密度；ir为道路坡度；δ为旋转质量换算系数；a为车辆加速度。

当车辆在平直路面行驶时，ir=0，此时行驶方程式可表示为

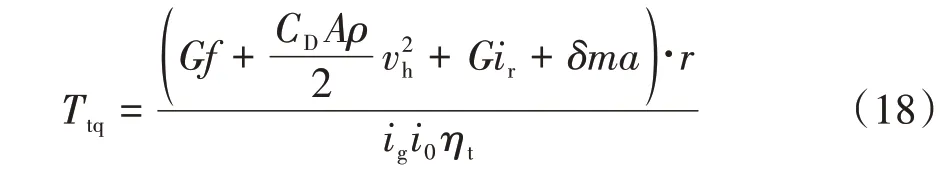
将期望加速度代入式（18）便可得到发动机期望转矩Tdes。根据3.1节中所选车辆模型的发动机map图数据在Simulink 中建立2-D Lookup 模块，便可根据期望转矩逆向求得发动机的期望节气门开度。发动机map图如图5所示。

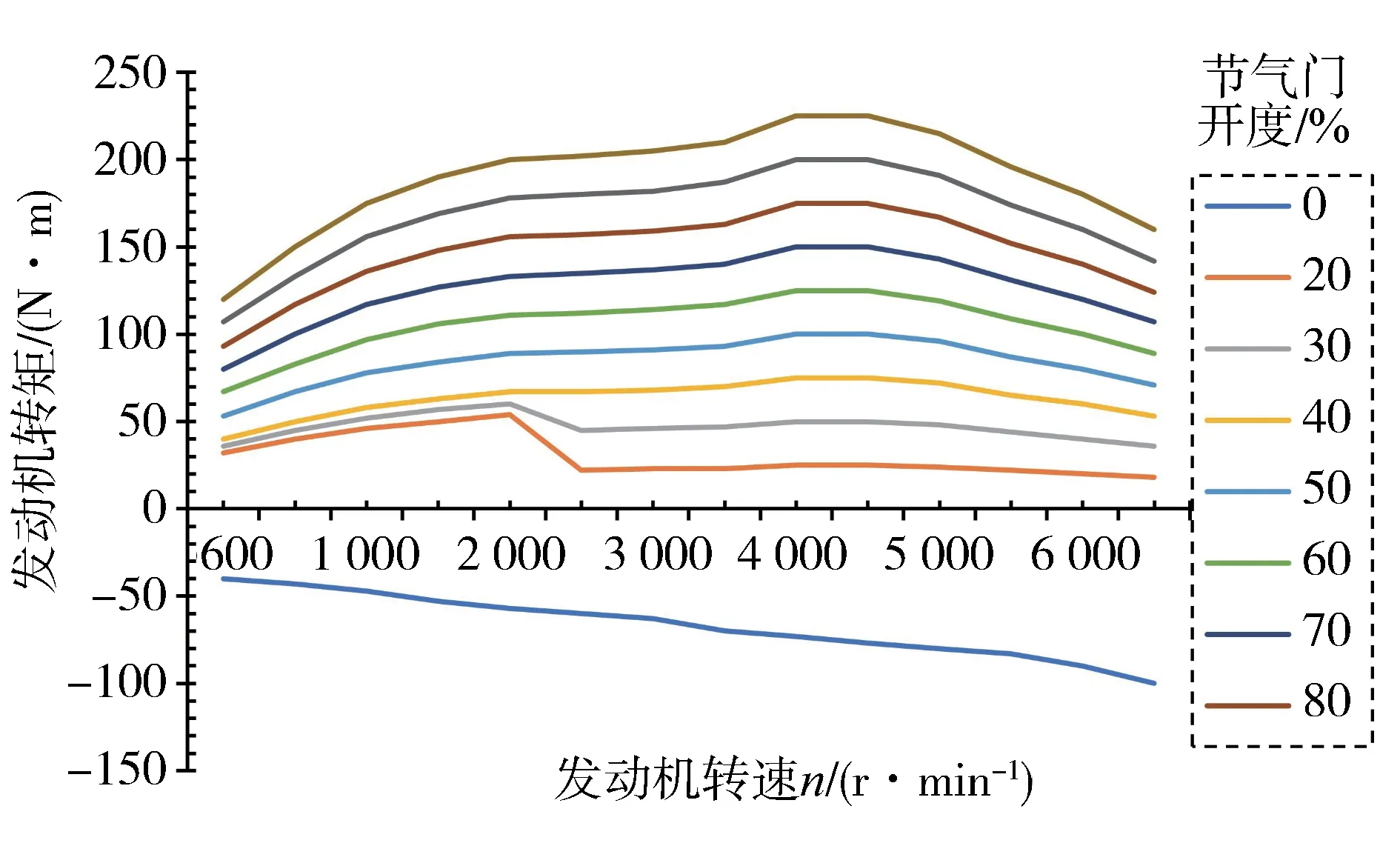
图5 发动机map图

3.4 制动压力控制模型

根据式（17）可推出制动过程中行驶方程式为

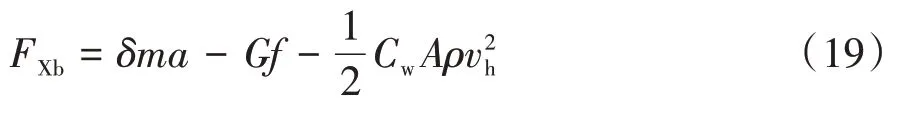
式中FXb为作用在车轮上制动力之和。车辆制动过程中其大小与制动压力p之间关系可通过比例系数来描述［22］，本文通过引入比例系数Kb表述二者之间关系：

通过在PreScan中设置加速试验，代入式(20)可得地面制动力大小，结合Simulink 车辆动力学模型中制动力值可计算出Kb为120。

4 仿真验证与实车验证分析

根据我国新车评价规程C-NCAP—2021 中对AEB 测试工况的规定，选取前车静止（CCRs）、前车运动（CCRm）2 种测试场景，每个场景设置3 组工况试验。相应的场景参数设置如表3所示。

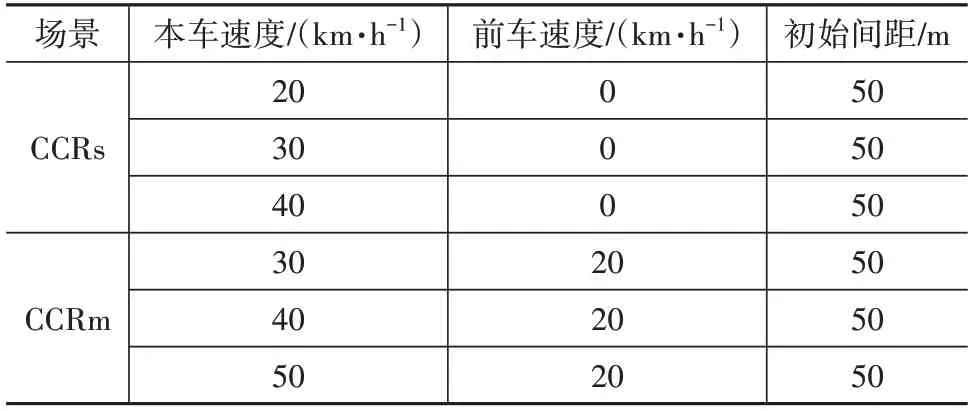
表3 仿真场景参数

4.1 CCRs场景仿真

CCRs场景仿真结果如图6所示。

图6 CCRs场景仿真结果

由图6 可知，本车以20 km/h 行驶时，在7.7 s 之前，由于紧急系数过小，系统判定为安全状态，保持匀速行驶，MPC 控制器不介入。7.75 s时，MPC 控制器开始输出期望加速度，此时车间距离为10.57 m，TTC为1.90 s，符合GB/T39901—2021 规定，此时紧急系数为0.57，系统采样时间为0.09 s，在8.95 s 时达到最大期望加速度-7.49 m/s2（此处最大期望加速度指绝对值最大，下同）。车辆在7.85 s开始执行期望加速度，整体迟滞约0.1 s，9.3 s时完成制动，制动距离为6.42 m，制动过程中采样时间由0.09 s 逐级降为0.06 s，加速度变化率最大为-8.24 m/s3，最终两车间距为4.12 m。根据文献［23］中试验分析，可以保障驾乘舒适性的加速度变化率极限值为-10 m/s3，因此符合舒适性与安全性预期。本车在以30、40 km/h 行驶时，制动开始时刻TTC值分别为1.93、1.84 s，加速度变化率最大分别为-8.39、-8.86 m/s3，均符合舒适性与安全性预期。如图6（b）所示，下层控制器跟踪性能良好，最大跟踪误差不超过2%，在紧急制动即将结束时由于车身的惯性导致实际加速度出现较小波动。

4.2 CCRm场景仿真

CCRm场景仿真结果如图7所示。

由图7 可知，本车以30 km/h 行驶时，在19.2 s之前，由于紧急系数过小，系统判定为安全状态，保持匀速行驶，MPC 控制器不介入。19.25 s 时，MPC控制器开始输出期望加速度，此时车间距离为6.83 m，TTC为2.44 s，紧急系数为0.2，系统采样时间为0.09 s，车辆在19.45 s 开始执行期望加速度并于20.15 s达到最大加速度-4.44 m/s2，整体迟滞约0.2 s，20.9 s 时两车间距达到最短4.18 m，加速度变化率最大为-8.79 m/s3，此后由于前车速度大于本车速度，两车间距逐渐增大，紧急系数也逐渐增大，本车期望加速度变为0。本车在以40、50 km/h 行驶时，制动开始时刻TTC值分别为1.81、1.46 s，加速度变化率最大分别为-8.27、-8.16 m/s3，制动过程中最小车间距分别为3.89、1.74 m，均符合舒适性与安全性预期。

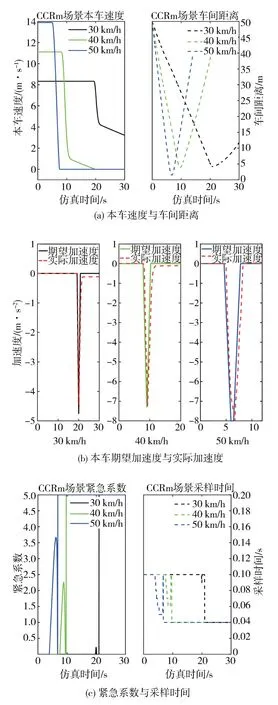
图7 CCRm场景仿真结果

4.3 实车试验分析

为进一步验证该策略的有效性与鲁棒性，本文建立吉利嘉际自动挡实车试验平台。试验平台与车辆如图8 所示，试验道路为封闭测试场地。基于系统性能要求及试验需要，对试验车辆加装自动紧急制动系统所需硬件，包括车载VCU 控制器、整车线束、毫米波雷达、V-Box 等。试验前按照GB/T39901—2021 对车辆进行加载与制动磨合、轮胎预处理等工作。目标车辆采用C-NCAP 中规定的包含视觉、雷达、激光雷达等属性的GVT，试验工况采用CCRs场景，为进一步检验用于实际车辆控制单元时的计算效能，本车以60 km/h 的时速驶向目标车辆，两车初始间距为100 m。试验结果如图9所示。

图8 吉利嘉际实车试验平台

由图9（c）可知，在3.85 s之前，由于紧急系数过小，系统判定为安全状态，期望加速度为0，但由于道路阻力等环境因素，试验车辆车速有下降趋势。3.85 s时，MPC 控制器开始输出期望加速度，此时车间距离为37.4 m，TTC为2.36 s，紧急系数为0.26，系统采样时间为0.09 s，在5.15 s 时达到最大期望加速度。车辆在4.55 s 时节气门完全关闭，制动压力开始上升，系统开始执行期望加速度，整体迟滞0.65 s，6.92 s 时完成制动，此时制动压力达到峰值12 MPa 并维持0.3 s 后逐渐降为0，制动距离为30.66 m，制动过程中采样时间由0.1逐级降为0.05 s，加速度变化率最大为-5.98 m/s3，最终两车间距为3.54 m，符合舒适性与安全性要求。

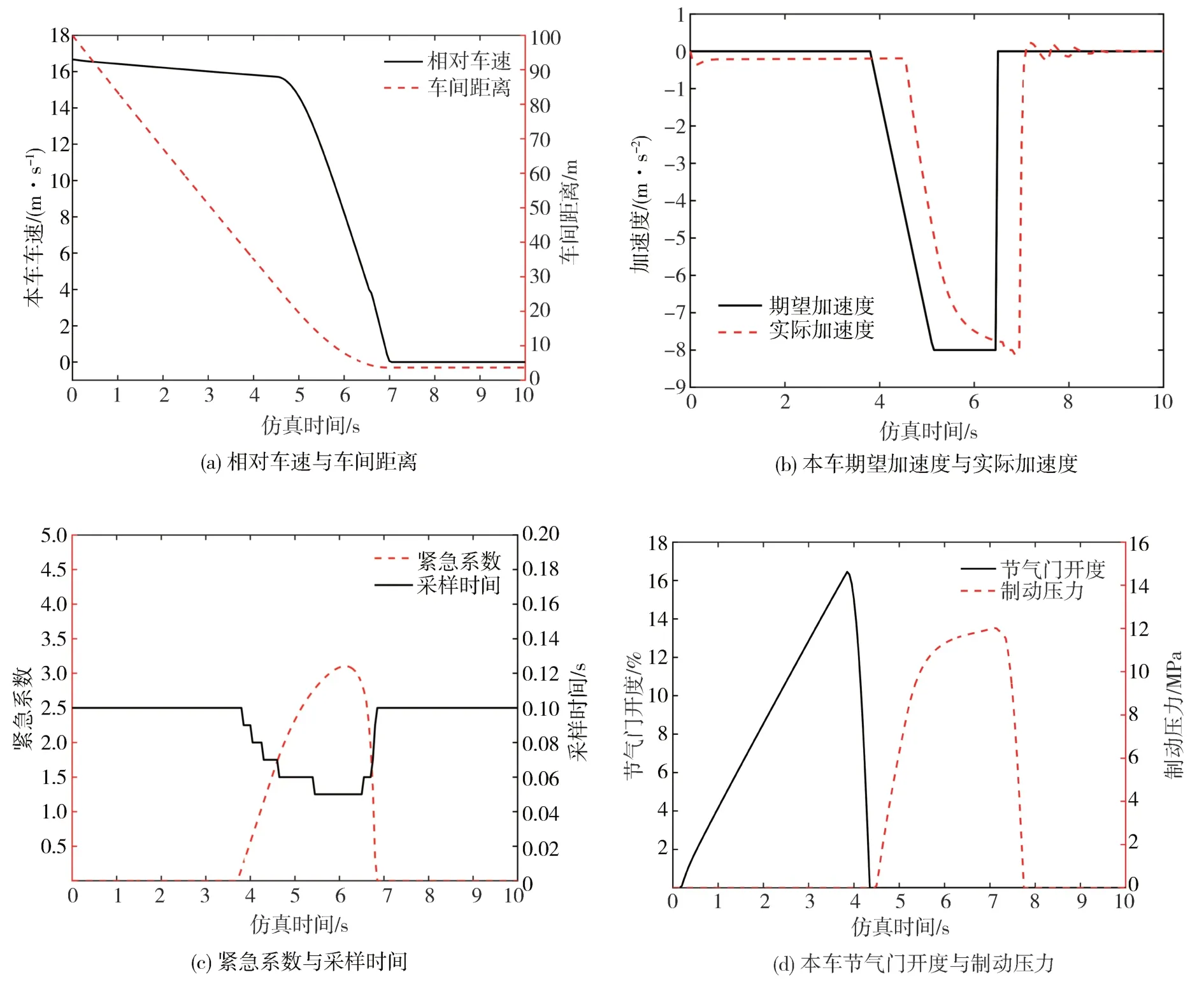
图9 实车试验结果

5 结论

（1）基于模糊规则MPC 算法与分层控制理论提出一种改进AEB 控制策略。上层控制器由模糊规则模块与MPC 控制器模块组成，模糊规则采取双输入、单输出，根据车间相对距离与TTC实时输出场景紧急系数，并根据该紧急系数优化MPC 控制器的仿真步长；下层控制器采用PID 反馈控制与逆发动机模型得到制动压力。

（2）在PreScan 与Simulink 联合平台上开展两种场景及多种工况下的仿真试验，验证了本文提出的控制策略可以兼顾自动紧急制动系统的舒适性与安全性。通过实车试验，进一步验证了系统的有效性。

（3）依托于MPC 控制器，为AEB 控制策略提供了新的解决思路。同时由于MPC 在自动驾驶领域具有较高的应用价值，研究内容将有助于推动AEB、ACC、ADAS 以及更高阶辅助驾驶系统一体化集成应用。