路面冲击输入下车内噪声主动控制*

2023-02-13王智豪徐中明夏子恒王虎成黄佳聪

汽车工程 2023年1期

王智豪，徐中明，夏子恒，王虎成，黄佳聪

（重庆大学机械与运载工程学院，重庆 400030）

前言

车内噪声性能一直以来都是汽车NVH 行业内非常关心的一个问题。随着国内汽车NVH 行业的快速发展，车内动力系统相关的NVH 性能已经取得了良好的成绩。并且随着汽车电动化的到来，与动力系统有关的噪声甚至会逐渐从车内消失［1］，因此，车内道路噪声控制的好坏将会是决定车内噪声性能高低的关键。车内道路噪声主要是由轮胎与路面摩擦时，出现轮胎沟槽的气泵现象和胎壁振动产生的，通过车身和悬架等结构传递到车内的低频噪声［2］。研究表明，基于声波的叠加原理，通过控制扬声器发出一个与初始噪声幅值相等且相位相差180°的声波，并与初始噪声进行干涉抵消，从而实现“以声消声”目的的噪声主动控制（active noise control，ANC）方法针对这种低频结构噪声有着良好的控制效果［3］。

车内噪声主动控制，自提出以来已经有了许多学者和科研单位开展了诸多研究［4-8］。Oh 等采用前馈滤波-x 最小均方误差（filterd-x least mean square，FxLMS）算法，通过使用4 个加速度参考信号，在粗糙路面上将车内道路噪声在50～500 Hz 范围内最大下降了6 dB［9］。Jung 等使用多通道前馈控制与远程传声器相结合的头枕主动噪声控制系统，对一辆越野车座舱内1 000 Hz以内的噪声实现了约3.7 dB的降噪量［10］。张立军等基于归一化的FxLMS 算法，在破损的粗沥青路面上取得了良好的效果［11］。上述研究都是以最小均方误差为准则的FxLMS 算法为基础的。

然而，汽车实际行驶的道路往往是复杂多变的，尤其是在路况变化时遇到短暂的冲击时（例如通过桥梁连接处或过减速带），基于传统FxLMS 算法的路噪主动控制系统鲁棒性较差［12］，在收敛过程中容易出现发散导致收敛失败的问题，进而产生刺耳的噪声，严重影响车内人员的驾驶感受和乘坐舒适性，在实车应用中有较强的局限性。

针对冲击工况下控制失效的问题，建立了基于滤波-x 最小平均绝对偏差（filterd-x least mean absolute deviation，FxLMAD）算法的车内路噪主动控制系统。采集冲击路面输入下的车内噪声并对其进行相关分析，从理论上说明FxLMAD 算法对冲击工况路面噪声主动控制的有效性。接着建立传统FxLMS 和归一化FxNLMS 与FxLMAD 算法的理论模型，分析不同算法的计算复杂度。然后将实车所采集的车内噪声数据作为输入进行仿真分析，验证其鲁棒性和计算复杂度及FxLMAD 算法的降噪效果。最后，基于数字信号处理器（digital signal processing，DSP）搭建车内噪声主动控制试验系统，实车道路试验证明基于FxLMAD 算法的车内路噪主动控制系统在冲击工况下的有效性。

1 路面冲击输入下车内噪声分析

1.1 路面冲击输入下车内噪声采集

在实际应用中，道路噪声常常会伴有不同程度的冲击，这类信号具有显著的尖峰，呈现脉冲性，因此不符合高斯分布。为分析冲击工况下道路噪声特性，采集试验车辆的路噪并进行相关分析。

参照 GB/T 18697—2002 《声学汽车车内噪声测量方法》，在主驾驶位头枕左右耳位置处分别布置1个传声器，采集车内噪声信号。试验中采用NI DAQmx 数采设备和MPA416 型传声器，相关硬件设备和传声器如图1 所示，采样频率为51.2 kHz，采样时长为10 s。

图1 数采和传声器布置

试验路面为干燥粗糙的平直沥青路面，天气晴朗无风，车窗关闭。车内乘坐驾驶员与后排测试人员两人，行驶速度为匀速50、60、70、80 km/h，在同一车速下采集两组通过该路段的数据以便分析。数据采集是在粗糙沥青路面中某段包含冲击的路段中进行，如图2所示。

图2 数据采集路面

1.2 路面冲击输入下车内噪声特性分析

以60 km/h 匀速行驶时采集的车内噪声为例进行时域和频域分析，所得结果如图3 所示。可以看出车辆在第8 s 时遇到强冲击，频率在150 Hz 以内。200 Hz 附近的空腔声较为突出，整体来看车内路噪以低频结构噪声为主，集中在300 Hz 内，部分低频空气噪声分布于300～500 Hz频率区间。

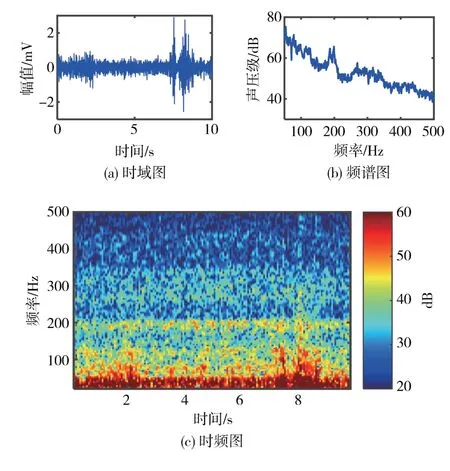
图3 冲击路噪特性分析结果

考虑到根据高斯模型推导出的FxLMS 算法对冲击噪声存在控制失效，因此需要确认上文采集到的噪声信号是否服从高斯分布。QQ 图（quantilequantile plots）是统计学里常用的判别某一组数据是否来自某个分布的方法。将该噪声时域数据作为输入样本进行统计学分析，绘制的QQ 图如图4 所示，与标准的正态分布相比，输入样本的QQ 图在两端相差极大，显然该样本的统计特性与高斯分布有着明显差别，对于这类非高斯统计特性的信号将不能采用基于高斯分布模型所设计的控制器来控制。

图4 60 km/h冲击路噪时域数据QQ图

汽车经过冲击性路面产生的脉冲性噪声为偏离平均值的异常大幅值信号，这些异常值使得整个样本的概率密度函数（probability density function，PDF）具有尖峰和厚尾的统计特征。对于这类样本，通常使用α稳定分布来描述［13］，α∈(0，2]是α稳定分布主要特征参数之一，α越小，该分布的PDF 有越厚的拖尾，表示远离中心位置样本的概率越大。为更直观地展示该噪声的非高斯性，绘制噪声数据的直方图和正态分布与α稳定分布的拟合曲线，如图5（a）所示。曲线的横坐标表示该噪声数据的幅值大小，纵坐标表示对应幅值在整个数据样本中出现的次数。从图中可以看出，相较于正态分布，α稳定分布可以更好地描述噪声数据的尖峰特征；同时对于两端的尾部数据来说α稳定分布具有更好的拟合精度。以前文分析的噪声数据作为输入样本，使用核平滑函数估计输入样本的PDF，接着绘制出输入样本对应的正态分布与α稳定分布的PDF，如图5（b）所示，分别计算出两种分布相对于输入样本PDF 的R2，其中α稳定分布的R(S)2=0.99明显高于正态分布的R(N)2=0.90，充分说明了对于路面冲击输入下车内噪声使用α稳定分布来建模能取得更准确的结果。

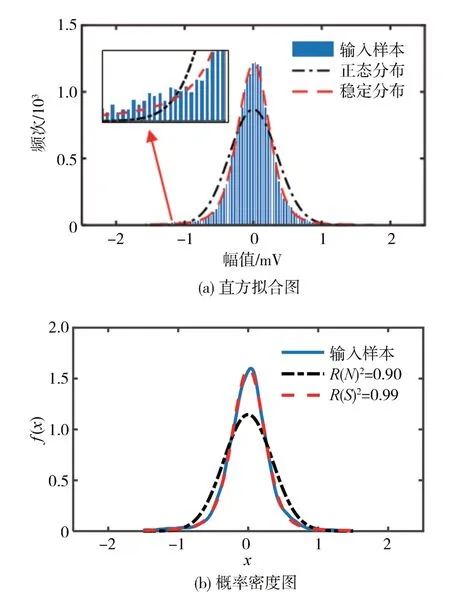
图5 两种分布的拟合对比图

α稳定分布的另一个重要特征是不存在有界的2 阶矩，α稳定分布样本的p阶矩仅当p≤α时存在［14］。而传统的噪声主动控制算法（FxLMS）都是以残余误差的2阶矩最小化为准则，在对符合α稳定分布的样本控制时，这些算法的降噪性能将会显著降低。

对上文1.1 节采集到的不同车速下的车内道路噪声使用α稳定分布进行拟合，得到对应的α特征值，具体数值如表1 所示。可以看出，表内的α特征值均小于1.7，说明车速在50～80 km/h 通过该冲击性路面输入路段的车内道路噪声均含有一定程度的脉冲性，并且随着车速的提高，α特征值逐渐降低，路噪信号脉冲性变强，这与车内人员的听觉主观感受保持一致。

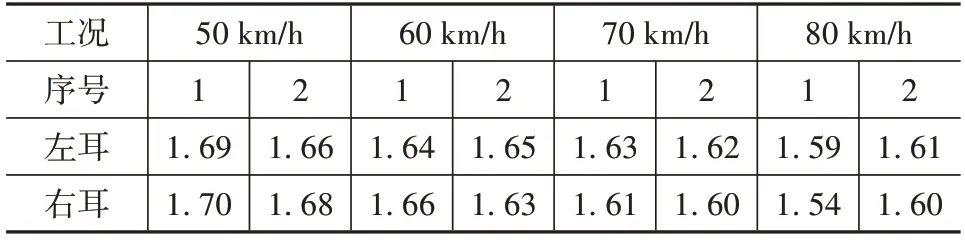
表1 不同工况路噪α特征值

2 车内噪声主动控制算法

2.1 多通道噪声主动控制系统

经典的多通道车内噪声主动控制系统框图如图6所示。

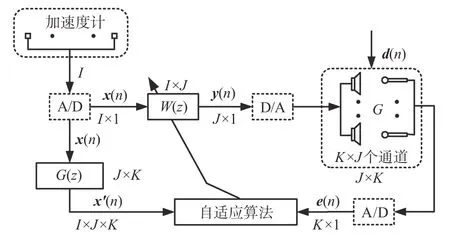
图6 车内路噪主动控制系统框图

图中x(n)=[x1(n)，x2(n)，…，xI(n)]T为I个参考传感器获取的参考信号；d(n)=[d1(n)，d2(n)，…，dK(n)]T为K个误差传感器处的噪声期望信号；y(n)=[y1(n)，y2(n)，…，yj(n)]T为J个次级声源发出的次级声信号；e(n)=[e1(n)，e2(n)，…，ek(n)]T为K个残余误差传声器信号；G(z)为J×K个次级通道的传递函数，可以用长度为M的FIR 滤波器表示；为对应的次级通道的估计。参考信号x（n）经过滤波后为滤波参考信号x′(n)；y(n)经过真实的次级通道G(z)滤波后到达误差传声器处与噪声期望信号相消。

由I个参考信号生成J个次级声源需要I×J个FIR滤波器，则第n时刻的第I阶的滤波器参数为

次级声源发出的信号是由I个参考信号经过I×J个滤波器的贡献之和，若取滤波器长度为L，有

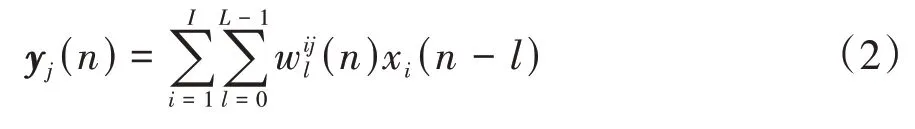
残余误差信号为噪声期望信号与在误差传声器处接收到的J个次级扬声器发出的次级声源之和：

若次级通道是时不变的，将上式重新整理可得

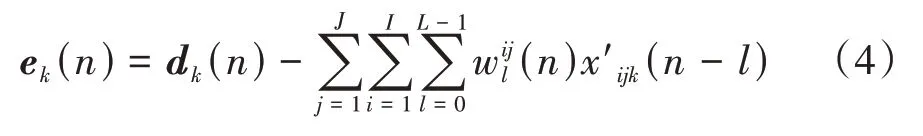
式中滤波参考信号为

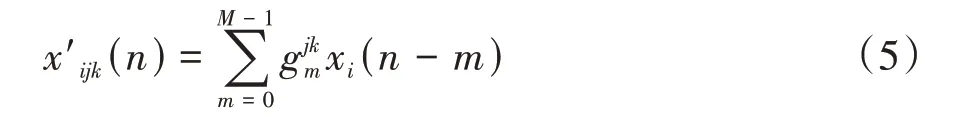
2.2 FxLMS算法

控制目标一般取为误差传声器处声压幅值2 阶矩最小，即目标函数为

式中E表示期望。为避免在求取滤波器权矢量最优解时进行矩阵的求逆运算，一般使用LMS 算法更新自适应滤波器，则第i个参考传感器到第j个控制器的滤波器权系数迭代公式为

上述便是多通道FxLMS 算法，该方法在面对非稳态噪声的情况下降噪效果有限，甚至会导致系统收敛发散。在实际的工程应用中，面对1.1 节的冲击工况路面时，在路噪主动控制系统中使用多通道FxLMS 算法会导致系统收敛失败，严重时系统会发出尖锐刺耳的噪声。

2.3 改进归一化MNFxLMS算法

为改善FxLMS 算法因为固定步长带来的鲁棒性较差等问题。Akhtar 等提出了改进归一化FxLMS（modified normalized FxLMS，MNFxLMS）算法［15］。MNFxLMS 算法是为了使得步长因子独立于输入功率，使用归一化的收敛系数实现自适应过程中收敛系数与稳态误差之间的均衡，加强系统对于非稳定声源的鲁棒性。MNFxLMS算法步长因子变化为

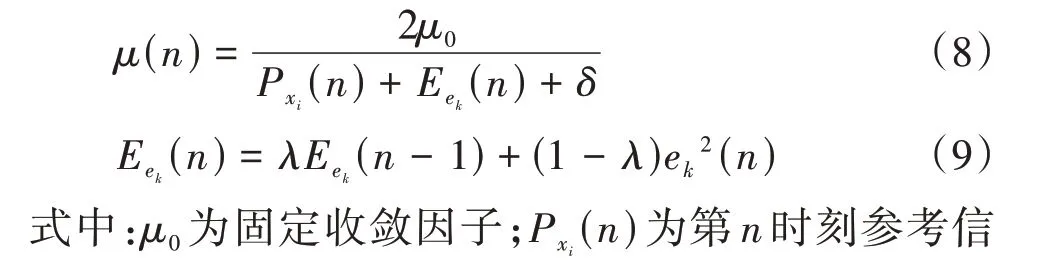
对于MNFxLMS算法，当参考信号或误差信号的幅值较大时，等效步长就会变小，因此可以有效避免权值更新过程中出现发散的情况。该算法在计算机仿真中对于非稳态噪声的控制能起到良好的效果，但其权值更新过程中每一次迭代均需要计算当前时刻的参考信号和误差信号的功率，计算量大，对硬件算力要求较高，因此很少在实际工程应用。

2.4 滤波-x最小平均绝对偏差算法

1.2 节说明了路面冲击输入下的车内噪声更适合用α稳定分布来描述其过程，对这类噪声信号而言，基于非高斯的α稳定分布模型的噪声信号处理算法，比基于高斯模型的算法具有更好的鲁棒性和稳态性能。Leahy 基于α稳定分布的特征，提出了最小化残差p阶矩的滤波-x 最小平均p范数（filterd-x least meanp-norm，FxLMP）算法［16］。其实质就是使控制目标函数由误差传声器处声压幅值2 阶矩最小化变为p阶矩最小化。即目标函数为

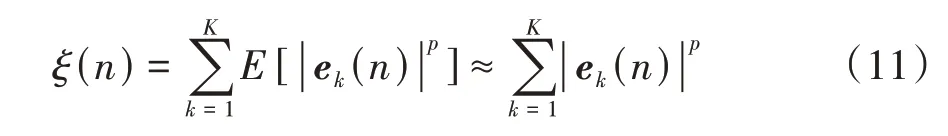
式中p＜a为分数低阶矩。则对应的滤波器权系数的迭代公式为

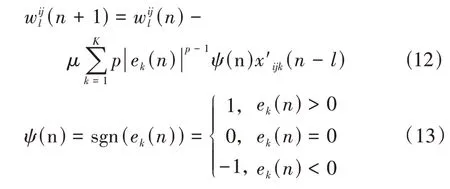
FxLMP算法对于包含脉冲性信号的冲击噪声可以获得良好的降噪效果，但需要特征参数α的先验信息。对于实际车辆行驶道路来说，路况是实时变化的，因此车内路噪信号的α是时变的。为了保证算法的稳定性，Bergamasco 提出了采用滑动窗实时在线估计α大小的改进FxLMP算法［17］。该算法虽然可以适应α的时变性，但每次权值迭代都需要计算误差信号的p阶矩，这将会大幅增加计算量。受到实际工程应用中硬件方面算力的限制必须降低该算法的计算量，Bergamasco 对于特征指数1 ≤α≤2 的样本，令FxLMP算法中的p=1，则该算法变为滤波-x最小平均绝对偏差（FxLMAD）算法［18］。其中滤波器系数的迭代公式为

不难看出，FxLMAD 算法是FxLMP 算法的一种特殊情况，由于p≤α的条件总能满足，FxLMAD 算法不需要对特征指数的先验需求，同时极大地降低了计算量。FxLMAD 算法的本质是对e(n)中大幅值的样本点进行限幅，避免由于大幅值的尖峰脉冲使权值在更新过程中发散。

2.5 算法复杂度分析

复杂度是评价算法性能的一个重要指标［11］。在工程实际应用中，一些复杂的算法往往因为硬件算力不够而无法实际应用。本节对上文提到的FxLMS算法、MNFxLMS 算法和FxLMAD 算法的复杂度以单个周期为例子进行对比分析，取L表示滤波器长度，M表示次级通道长度，结果如表2 所示。在实际应用中，噪声主动控制算法的实现通常是基于高性能数字信号处理（DSP）芯片的控制器。本节以亚德诺半导体（ADI）公司的ADI21565 芯片为载体，直观地比较了上述AINC 算法的计算复杂度。DI21565 芯片的单指令周期为1.00 ns，计算中涉及的变量均采用32位浮点型，常用运算所需的指令数如表3所示。不难看出，除法运算的计算量远远高于乘法运算。此外，指数和对数运算需要大量的计算资源。

表2 计算复杂度比较

表3 常见操作的指令数

与下文相同，滤波器长度L和次级通道长度M均取为128，根据表2 与表3 中的数据计算出FxLMS算法、MNFxLMS 算法和FxLMAD 算法在单个周期内的指令数分别为5 115、6 485 和5 142。以FxLMS 算法指令数为基准，MNFxLMS 算法与FxLMAD 算法的指令数分别增加26.8%和0.5%，后者增加的计算量极低。

3 车内路噪主动控制仿真

为验证不同算法对包含脉冲信号路噪的有效性，在MATLAB/Simulink 中建立多通道路噪主动控制模型，该模型中的参考信号数量为8，次级声源与误差传声器数量均为2，以前文1.1节所分析的车内噪声数据作为输入进行仿真。

3.1 次级路径获取

为了使仿真结果更可靠，选取实际车内测得的次级路径作为模型中的次级路径估计。在驾驶员位置的左右耳位置分别布置一个聚声泰A2B数字传声器（GM26-V063）作为误差传声器，座椅上的头枕扬声器作为次级声源，布置形式如图7 所示。控制每个次级声源依次发出50～500 Hz 的扫频噪声，误差传声器同时进行采集，使用LMS 算法离线获得次级路径的估计值。

图7 次级声源与误差传声器布置

实车次级通道的滤波器系数如图8 所示，每幅子图包含了该位置扬声器到2 个误差传声器处的2个滤波器系数。次级路径的滤波器阶数选取为128阶。

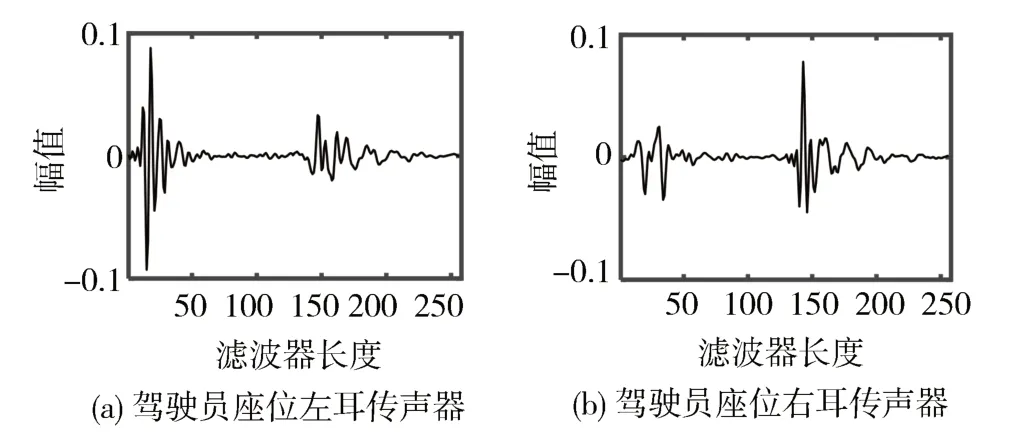
图8 扬声器到2个误差传声器的滤波器系数

3.2 仿真结果分析

将仿真数据和辨识得到的次级路径通道导入到Simulink 中，采样频率设置为2 kHz，3 种算法的仿真结果对比如表4所示。

表4 仿真结果

在60 km/h 的匀速下，MNFxLMS 算法和FxLMAD 算法降噪量差别不大但均远好于传统的FxLMS 算法。图9 为60 km/h 各位置的频谱分析结果，可以看到，MNFxLMS算法和FxLMAD 算法在50～500 Hz 均能取得有效的降噪效果，尤其是在低频50～200 Hz取得的降噪效果更为明显，说明了这两种算法在控制包含脉冲性噪声时的有效性。考虑到FxLMAD 算法的计算量更低，因此有更好的实际应用价值。

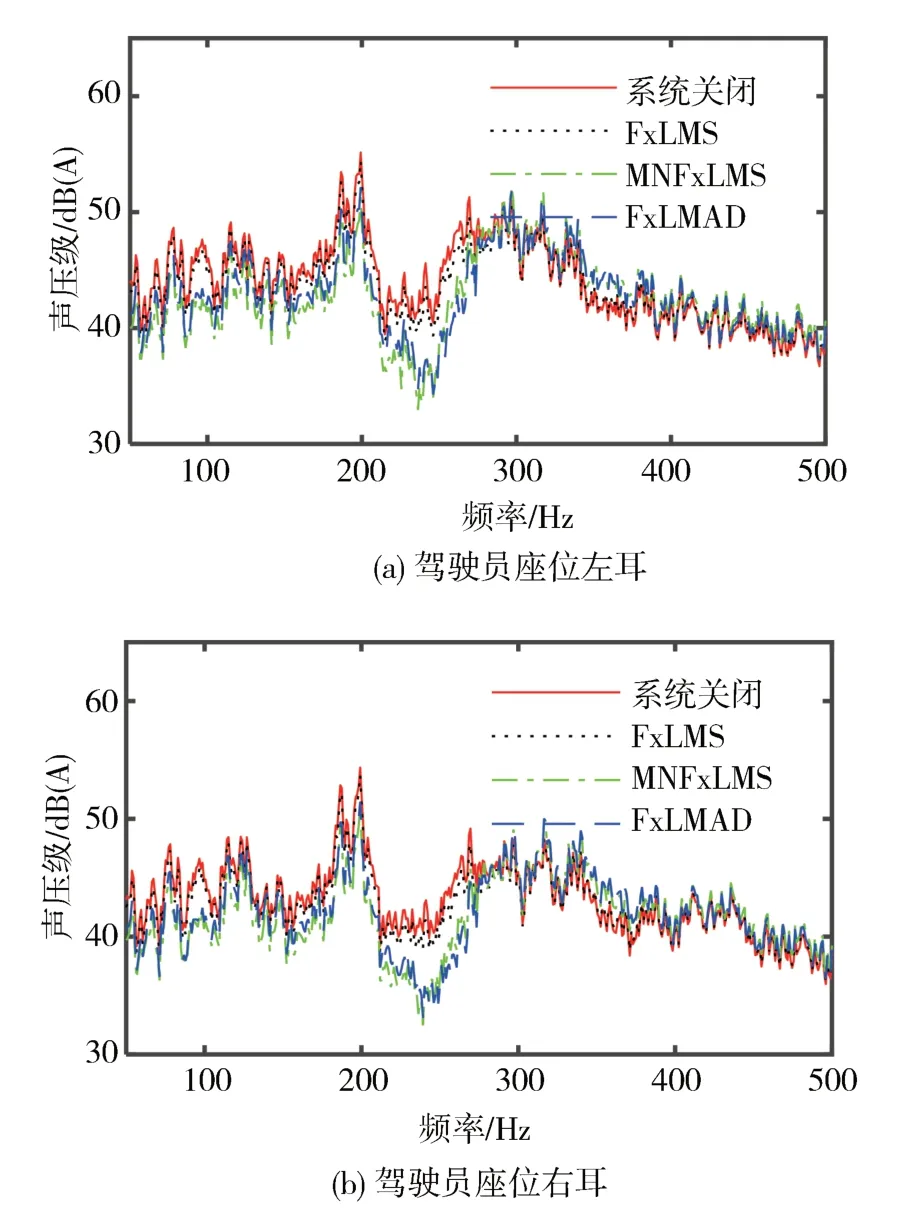
图9 60 km/h仿真结果

4 实车试验

4.1 试验概况

为验证所提方法的可行性，在某款燃油SUV 乘用车上进行车内路噪主动控制系统实车道路测试。采用与仿真相同的次级声源、误差传声器和相同数量的参考信号。系统的8 路参考信号来自于底盘与悬架处的共4个PCB 356A32型加速度计。这4个加速度计安装位置的选取方法使用多重相干法为基础［19］，通过枚举法列出基于12 个初选点的所有参考信号组合，最后选择车内噪声多重相干系数最大的参考信号组合作为终选结果，其实车安装位置如图10所示。

图10 加速度传感器布置

多通道路噪主动控制系统的硬件原理框架图如图11 所示，误差信号到达A2B 传声器后，与汽车底盘处加速度计所获取的振动信号共同通过由主收发器AD2428 和从收发器AD2426 构成的A2B 链路上传至DSP，当DSP 中的存储器数据到达设定长度时，运行多通道FxLMAD 算法，算法生成的次级声信号再经过数模转换和功放后驱动扬声器发声。

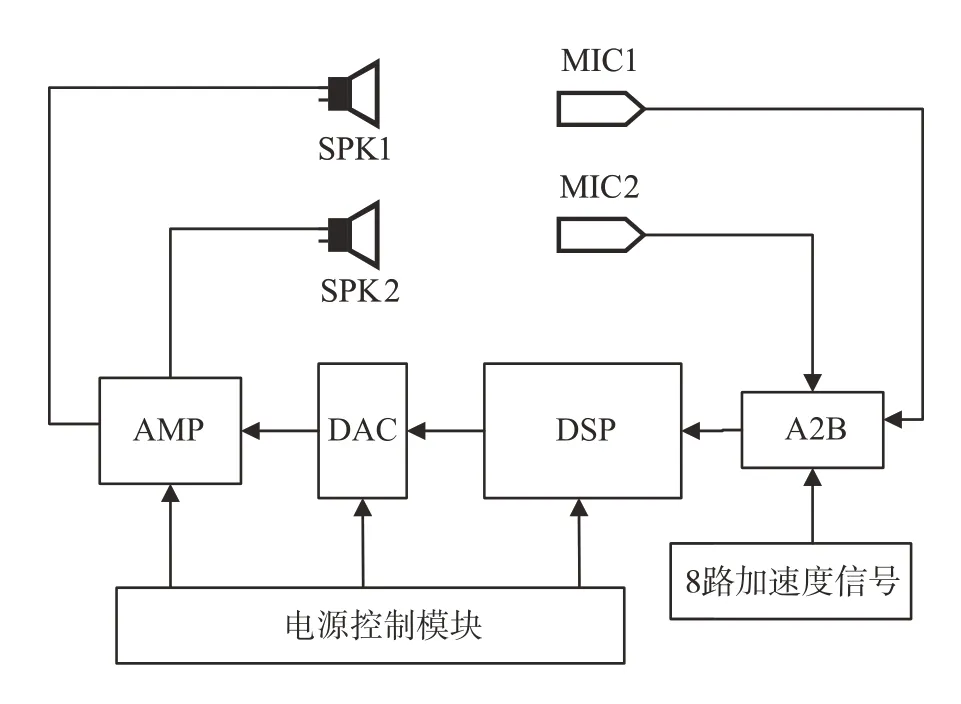
图11 硬件原理框图

在A2B误差传声器旁放置一个MPA 416型监测传声器，用以采集降噪效果，采样频率为51.2 kHz数采设备为NI DAQmx。底盘加速度计与A2B 误差传声器采样频率均为48 kHz，为提高计算效率在进入硬件系统后均降采样为2 kHz。整个硬件系统主要由一块集成了数字功放和MCU、A2B 主收发器、DSP 芯片的PCB 开发板构成。其中芯片型号为ADI公司的ADSP-21565、MCU 型号为恩智浦FS32K144 HAT0MLHT、A2B主、从收发器型号为AD2428和AD2426。其余设备还包括供电电源、线束等。试验车辆和DSP控制器如图12所示。

图12 车内路噪主动控制平台

4.2 试验结果分析

试验路面选择为粗糙沥青路面中某段包含冲击的路段，测试时速度分别为50、60、70 和80 km/h 匀速行驶。试验开始时提前打开噪声主动控制系统，等待5 s系统收敛后开始数据采集；系统关闭时则直接采集数据。数据采集时长均为10 s，对比噪声主动控制系统开启和关闭后相应的噪声信号。为提高测试结果的可信度，对不同车速下不同算法控制系统未开启状态下的车内噪声进行对比。以80 km/h车速为例，其频谱对比图如图13所示。

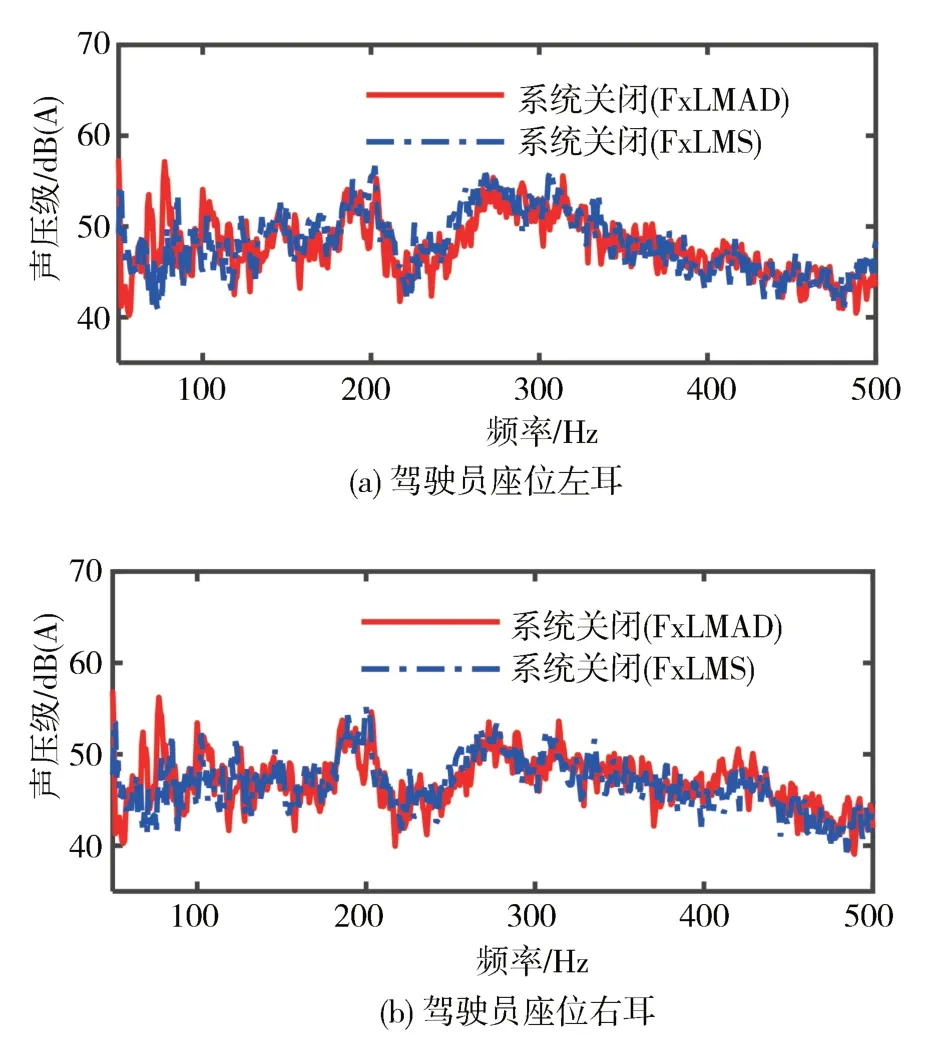
图13 80 km/h系统关闭时噪声对比

从图中可以看出，在同一车速下，两种系统关闭时的噪声功率相差不大，在50～500 Hz 范围内，将系统关闭时（FxLMAD）车内噪声的总声压级（A 计权）减去系统关闭时（FxLMS）车内噪声的总声压级（A计权），得到两种算法在系统关闭时前者较后者在右耳处增量为0.4 dB，左耳处为-0.4 dB。4 种车速下两种系统关闭时的车内噪声声压级差值均在1 dB以内。实车道路测试结果如表5 所示，同仿真结果类似，FxLMAD 算法的降噪效果优于传统的FxLMS算法。

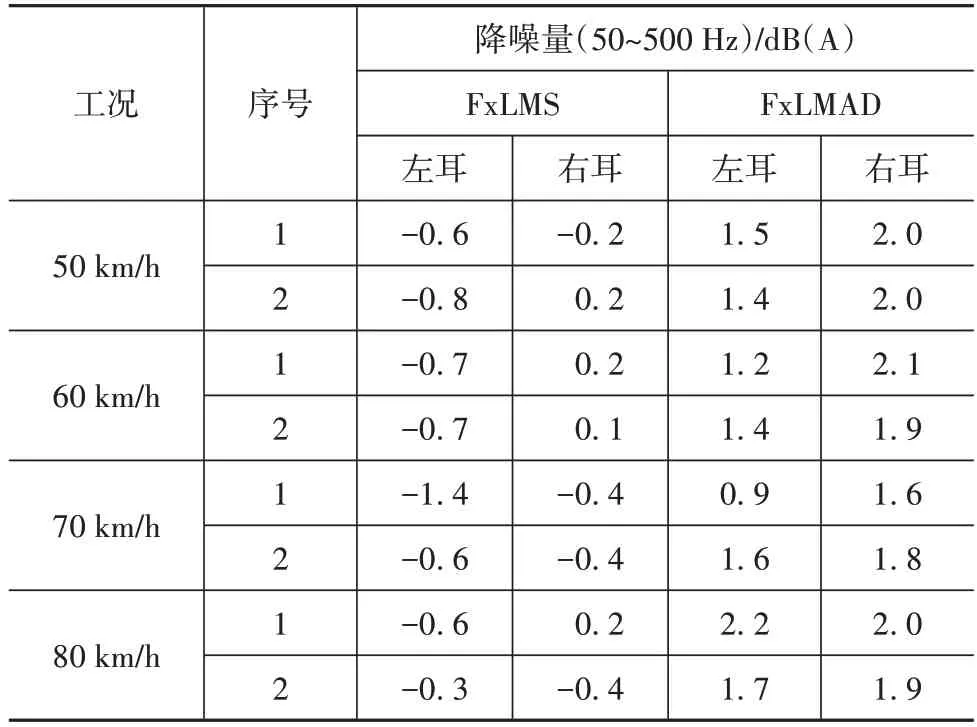
表5 试验结果

以80 km/h 降噪效果为例，此时左右耳在50～500 Hz 频带内的总声压级分别下降了2.2 和2.0 dB（A），而传统的FxLMS 算法中，左右耳在50～500 Hz频带内的总声压级的降噪量为-0.6和0.2 dB（A）。

图14 和图15 为80 km/h 道路测试频谱和1/3 倍频程对比结果。可以看出，传统算法在200 Hz 以下的低频部分控制早已失效，甚至产生了负向的降噪效果，而这一频段对应的正好是整个路面中含有脉冲性的部分，传统的FxLMS 算法对冲击工况路面依然失效。在80～200 Hz内，FxLMAD 算法相较FxLMS算法有更好的噪声控制效果，80 Hz以下的频带没有得到有效的控制，其原因可能是被试验中所使用的扬声器频响限制。

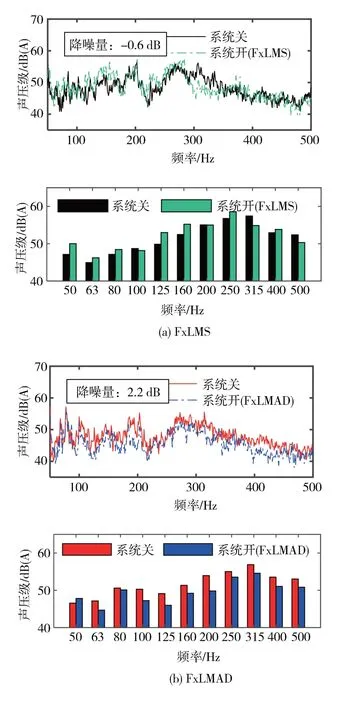
图14 80 km/h道路测试结果（驾驶员座位左耳）

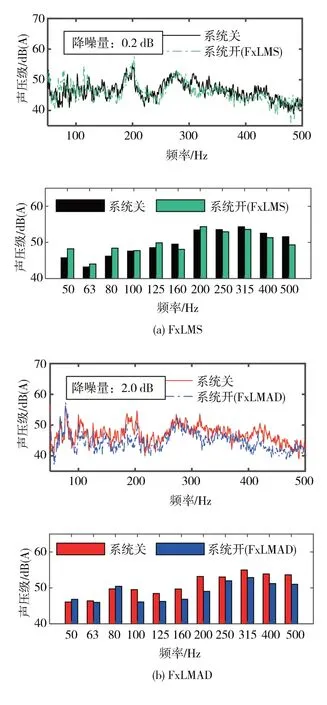
图15 80 km/h道路测试结果（驾驶员座位右耳）

试验结果表明，车辆在不同车速下，使用FxLMAD 算法的降噪系统在50～500 Hz 范围内的总声压级降噪量均可以达到约2 dB（A），综上所述，FxLMAD 算法在具有冲击性信号的噪声下相较于传统的FxLMS 算法有良好的稳定性，从而使整个工况取得了更好的降噪效果，验证了FxLMAD 算法在包含冲击性信号的路面噪声主动控制中的有效性。