高性能预应力胶合木张弦梁长期受弯蠕变模型研究

寇素霞

(东北林业大学 土木工程学院，哈尔滨 150040)

0 引言

蠕变是黏弹性材料重要特征，即在荷载持续作用下，随时间的推移变形增大的现象。木材是一种蜂窝状高分子材料，包括纤维素、半纤维素和木素等多种组成成分，属于典型黏弹性材料，具有明显的蠕变特征[1]，因此，以木材为原料制成的工程木制品，用于建筑结构中，在长期荷载作用下，木构件的强度和变形能力均会发生改变，其蠕变特性亦会影响结构使用的舒适性。预应力胶合木张弦梁在长期荷载作用下产生蠕变，既会对木材的力学性能产生影响，也会改变预应力筋应力大小，这是由于长期荷载作用下，锚固形式以及温度变化等原因会造成预应力筋应力松弛，导致施加在预应力胶合木张弦梁上的预加力减小，造成预应力损失，形成预应力胶合木张弦梁抗弯性能降低的结果。

目前对于蠕变的研究主要通过对短期蠕变试验数据的分析，来预测木材长期蠕变[1-3]。虞华强等[4]仅就木材的蠕变预测模型进行了总结和归纳，但对各种蠕变模型合理性没有给出意见和建议。陆伟东等[5-6]研究了采用纤维材料增强胶合木梁蠕变性能，分别使用了四参量模型和Findley模型，进行推导分析胶合木梁和纤维材料的蠕变。Li等[7]研究了玻璃纤维增强聚合物(GFRP)面板和轻木的复合夹层梁的弯曲蠕变，采用Bailey-Norton模型和Findley模型预测结构蠕变变形随时间变化规律。团队前期[8-11]试验研究了预应力胶合木梁弯曲蠕变性能。

本研究探讨了长期荷载作用下预应力胶合木张弦梁的蠕变模型适配性。首先进行预应力胶合木张弦梁的长期加载试验[12]，通过试验实测数据，得到各类蠕变模型下材料的蠕变应变表达式，将试验结果与蠕变应变表达式进行拟合，确定模型中待定力学参数，验证各类模型的可行性。在土木工程领域中，预应力木结构也具重要作用，本研究在设计应力方面对实际工程有理论指导作用。

1 试验概况

1.1 试件设计及分组

为了得到长期荷载作用对预应力胶合木张弦梁受弯性能的影响，试验选择在相对稳定的环境条件中进行，试验地点为哈尔滨室内试验室，温度维持在20 ℃±3 ℃范围内，相对湿度维持在70%±5%，试验持续载荷225 d，基本保证试验全程环境温度和相对湿度的基本稳定，便于对梁的蠕变性能进行分析比较。

试验按预应力调控程度，即所加初期荷载的不同，分为5种工况，包括1组对照组不调控胶合木梁，不同调控程度的张弦梁各1组，取短期试验极限荷载的7.5%～30.0%均匀分级。所有试验胶合木梁均为沿梁高方向由5层20 mm厚的樟子松板材胶合而成，尺寸为3 150 mm×80 mm×100 mm，以前期理论为支撑，取短期抗弯试验极限荷载的30%作为长期受弯试验梁的加载值[12]。试验梁详细分组情况，见表1。

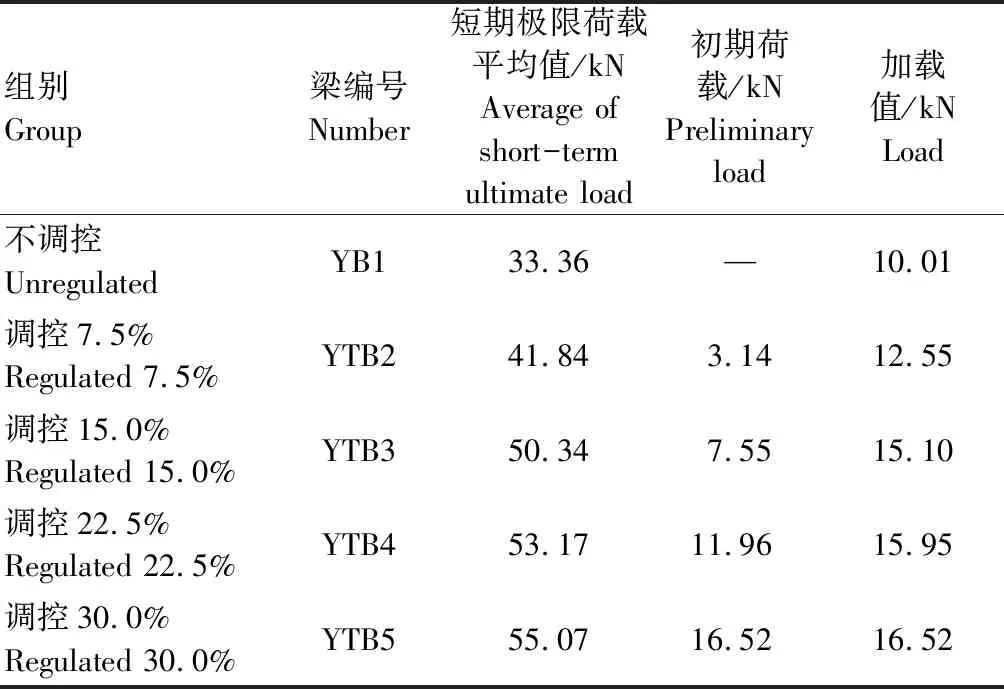
表1 预应力胶合木张弦梁分组Tab.1 Grouping of prestressed glulam string beam

1.2 加载装置及测点布置

试验采用四点弯曲方式进行加载，梁跨中挠度和钢筋应变等数据通过位移计和应变片来采集。位移计分别在梁端支座及跨中放置，应变片分别在胶合木梁的2个加载点以及试验梁跨中胶合木梁侧面和钢筋中心位置进行布置，加载装置及测点布置，如图1所示。

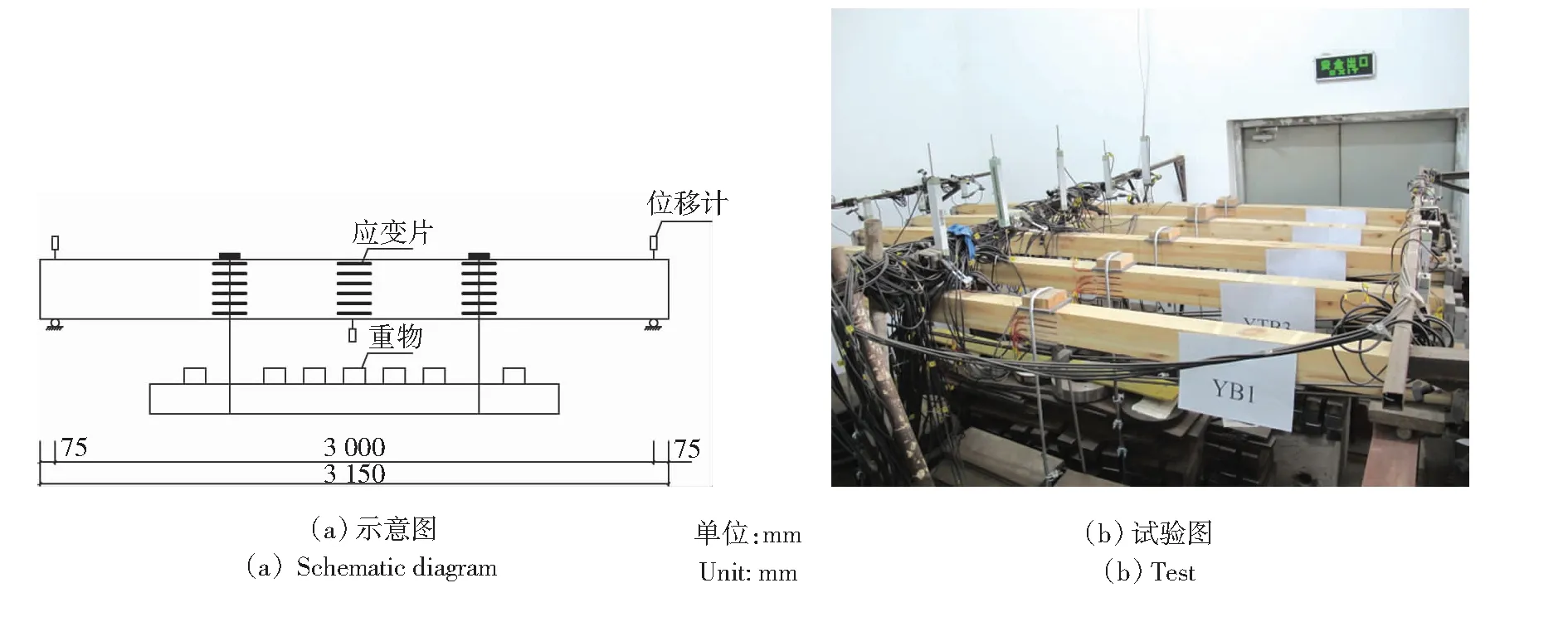
图1 加载装置及测点布置

2 结果与分析

2.1 试验现象

对试验全程进行观察，每隔75 d对胶合木梁的蠕变现象进行一次拍照记录。由于试验加载值相对较低，所以试验梁在加载期间状态基本稳定。取一组典型试验梁为代表，描述试验现象。以YTB5组为例，与试验第1天相比，到试验第75天时，在木梁缺陷位置出现破坏，如木节附近位置出现轻微裂缝；到试验后期时，破坏现象无明显发展，如图2所示。

图2 长期试验YTB5的状态Fig.2 YTB5 of long-term test

2.2 试验结果

长期抗弯试验，试验梁跨中挠度包括预应力产生的反拱、施加荷载产生的跨中变形和胶合木随时间变化产生的变形等，通过绘制时间-挠度关系曲线，进而得到不同调控程度的预应力胶合木张弦梁长期挠度发展规律，如图3所示，图中纵坐标为负，表示挠度向上。

图3 跨中挠度随时间变化曲线Fig.3 Mid-span deflection time curve

3 蠕变模型研究

3.1 蠕变模型类型

目前常用木材蠕变模型大都属于唯象模型，分为经验模型和力学模型2类。经验模型一般是以数学方程为基础建立预测构件的蠕变变形随时间变化的回归方程，包括：幂律模型、对数模型和指数模型等[11-13]；力学模型一般是通过理想弹性和黏性元件按一定规则构成建立预测未来蠕变发展的力学方程，常见模型：Kelvin模型、Maxwell模型和Burgers模型等[14]。各模型基本形式如下。

(1)幂律模型

幂律方程是将蠕变看成一个连续的发展过程，其基本形式为

y=atb+c。

(1)

式中：y为构件的蠕变量；t为构件发生蠕变变形的时间；a、b、c为待定系数。

(2)对数模型

对数方程可将材料蠕变的发展看作2个过程，分别是一个短期过程和一个长期过程，其基本形式为

y=a+blnt。

(2)

式中：y为构件的蠕变量；t为构件发生蠕变变形的时间；a、b为待定系数。

(3)指数模型

指数方程建立的蠕变模型在于不同研究可采用不同f(t)，其基本形式为

y=a(1-ef(t))。

(3)

式中：y为构件的蠕变量；t为构件发生蠕变变形的时间；a为待定系数；f(t)为关于t的函数。

(4)Kelvin-Voigt模型

是由一个理想弹性体和一个黏壶元件并联组合而成，如图4所示，能较好模拟木材的蠕变过程，但不能模拟瞬间弹性，其基本原理如下。

E为弹性模量；η为黏度。

σ=σs+σd。

(4)

式中：σ为应力；σs为弹簧应力；σd为黏壶应力。

依据模型性质

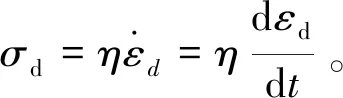
(5)

将公式(5)代入公式(4)中，令应力为常数，可得

(6)

式中：σ0为瞬时应力；ε为应变。

对公式(6)进行微分方程求通解(εh)

(7)

式中，c1为任意常数。

假定特解εp为

(8)

将公式(7)和公式(8)进行整理，得到微分方程完整解

(9)

令ε(0)=0可得，Kelvin-Voigt模型的本构方程

(10)

式中，β1、β2为待定参数。

(5)Maxwell模型

是由一个理想弹簧和一个理想黏壶串联组合而成，如图5所示，其基本原理如下。

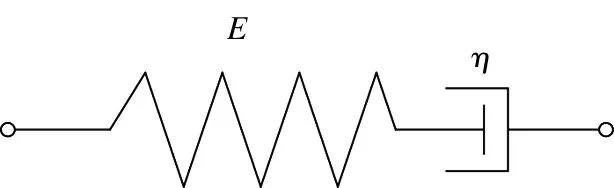
图5 Maxwell模型示意图Fig.5 Diagram of Maxwell model

ε=εs+εd。

(11)

等式两边进行微分，将公式(5)代入公式(11)中，整理后可得

(12)

假定σ趋于零，整理后可得

(13)

令ε(0)=0可得，Maxwell模型的本构方程

(14)

(6)Burgers模型

Burgers模型又称四元件模型，由一个Maxwell模型与一个Kelvin模型组合而成，如图6所示，其基本形式如下。

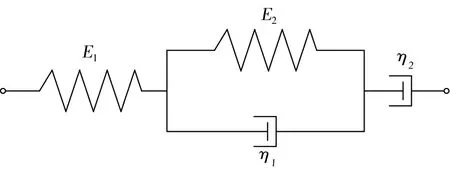
E1、E2分别为Maxwell模型、Kelvin模型的弹性模量；η1、η2分别为Kelvin模型、Maxwell模型的黏度。

β1+β2(1-e-β3t)+β4t。

(15)

3.2 参数拟合与模型分析

将蠕变变形的本构模型与试验数据进行拟合，得到模型各项系数，进而预测稳定条件下木材蠕变发展情况，现对各种模型下长期试验梁蠕变变形情况进行分析，各梁蠕变拟合曲线，如图7所示。

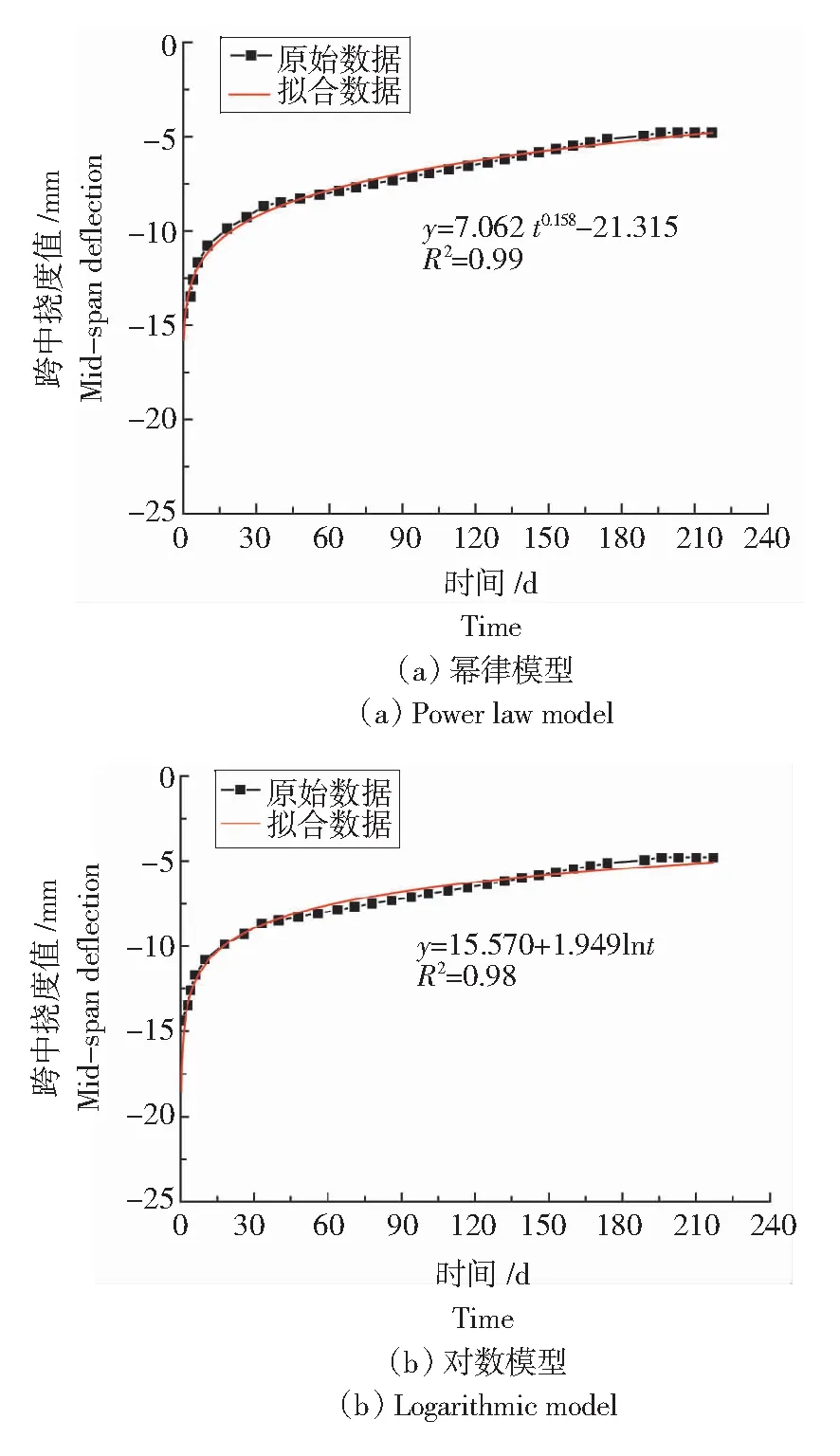
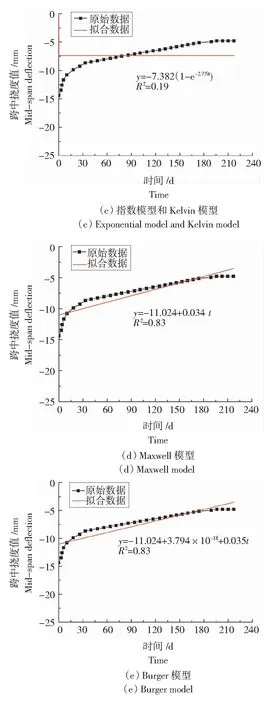
图7 各蠕变模型拟合曲线Fig.7 Fitting curves of various creep models

各经验模型拟合曲线的试验参数a、b、c及相关系数的平方(R2)见表2，各力学模型拟合曲线的试验参数β1、β2、β3、β4及相关系数的平方(R2)见表3。

表2 经验模型拟合参数结果

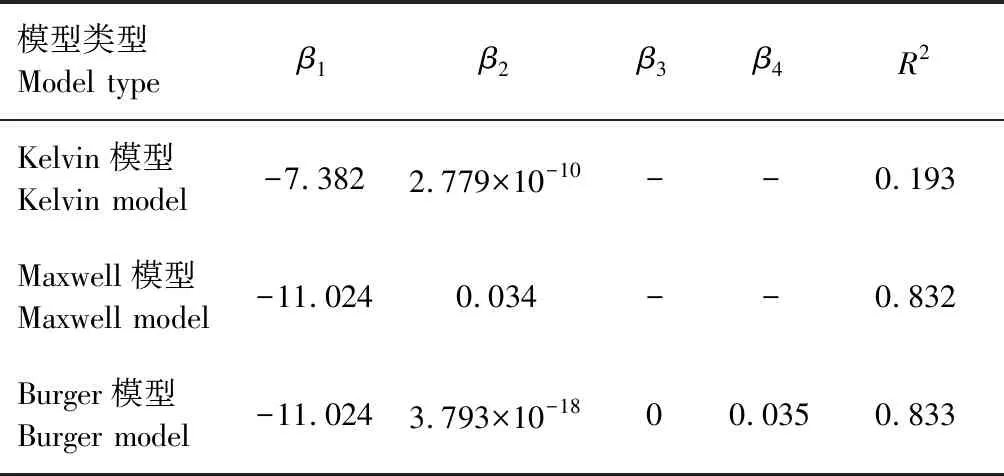
表3 力学模型拟合参数结果Tab.3 Mechanical model fitting parameter results

从图7、表2和表3可以看出，就预应力胶合木张弦梁而言，幂律模型、Maxwell模型和Burgers模型拟合效果较好，拟合整体相关系数的平方(R2)接近于1，3种模型的拟合曲线与试验曲线吻合度相对较高。各模型中，幂律模型拟合参数较少，计算简单通用，其拟合结果的精确度比力学模型高，但经验蠕变模型以数学方程式为基础，仅能够表现出木材的蠕变变形，无法反映出预应力损失造成的影响，具有一定的局限性；力学模型能够完整地反映出组合梁各材料在长期荷载作用下的变形规律，但考虑的影响因素较多，拟合参数较多，计算较为复杂；将各蠕变模型进行推导整理后发现，采用试验的预应力胶合木梁建立的指数模型和Kelvin模型表达式相同，均无法拟合预应力胶合木张弦梁蠕变曲线。

4 结论

本研究基于预应力胶合木张弦梁长期受弯试验，分析常见各类木材蠕变模型的适配性，得出以下结论。

(1)在试验期的长期荷载作用下，预应力胶合木梁的蠕变曲线仅存在初始蠕变和稳定蠕变两个阶段。初始蠕变阶段，变形速率递减，15 d后曲线的斜率达到相对稳定，曲线进入稳定蠕变阶段，变形曲线表现为线性变化，变形速率基本保持不变，预应力胶合木梁的长期荷载取极限荷载的30%时，长期变形基本稳定。

(2)将长期受弯试验结果用各类常见模型进行拟合对比，经验模型能够较好地反映预应力胶合木张弦梁的蠕变特性，幂律模型和对数模型拟合整体相关系数的平方(R2)分别为0.99和0.98，二者均能较为准确地预测梁长期蠕变规律；力学模型拟合整体相关系数的平方(R2)为0.83，仅能够大致地反映预应力胶合木张弦梁的蠕变特性和蠕变变化趋势。