Q235钢与304不锈钢多层爆炸焊接的数值模拟研究
2023-02-11缪广红杨礼澳艾九英祁俊翔马秋月孙志皓马宏昊沈兆武
缪广红,胡 昱,杨礼澳,艾九英,祁俊翔,马秋月,孙志皓,马宏昊,沈兆武
(1.安徽理工大学 力学与光电物理学院,安徽 淮南 232001;2.安徽理工大学 土木建筑学院,安徽 淮南 232001;3.安徽理工大学 化学工程学院,安徽 淮南 232001;4.中国科学技术大学 中国科学院材料力学行为和设计重点试验室,合肥 230027)
1 引言
随着工业技术的发展,双金属复合板因其优异的机械性能和耐腐蚀性而被广泛应用于化工原料传输、空间站维护、海底管道连接等行业,成为了特种作业环境中设施的首选材料[1]。作为制备双金属材料的常用方法,退火冷轧、摩擦焊接、爆炸焊接等在生产中均能够取得良好的效果,但其各自的生产侧重点并不一致。退火冷轧只能用于加工简单形变材料,摩擦焊接则适合在中小型零件中建立接头,而爆炸焊接则可应用于大型异种金属板材的一次性复合[2]。作为一种固态连接技术,爆炸焊接利用炸药爆炸赋予了复板高速冲击基板的能力,伴随碰撞过程中的高温高压基复板结合点会喷射出金属射流,从而促使基复板之间形成特殊的波浪状结合界面,这是判定双金属复合板是否达到高质量结合的标准之一[3]。
传统爆炸焊接多采用单层装药的方式加工金属材料,这种装药手法胜在稳定且易控制,然而其炸药利用率却并不乐观,爆轰产物所携带的爆炸能有相当部分扩散至空中未能得到利用,还间接带来了一定程度的噪音污染和空气污染。Xu等[4]提出了一种利用炸药覆盖层控制爆轰产物的装药方式,有效提升了炸药利用率;Daichi等[5]利用水下斜角装药成功复合了钨与F82H素体钢,控制了爆炸产物的次生污染;Yang[6]综合了双面爆炸焊接的方法,以多层爆炸焊接法一次实验制备了5组复合金属材料。本文以ANSYS 19.0软件为工具,分别采用SPH-FEM耦合法和SPH法对Yang[6]提出的多层爆炸焊接进行了三维与二维数值模拟,充分对比了实验与模拟中获得的动态参数,分析了基复板结合界面的波形分布情况。
2 模型设计
2.1 计算模型
以文献[6]中所给出的多层爆炸焊接实验为基础,利用ANSYS 19.0软件建立计算模型。实验分为两组,图1(a)为多层爆炸焊接组的结构图,其自上而下分别由一组单面爆炸焊接装置和两组双面爆炸焊接装置构成,为对比双面爆炸焊接与单面爆炸焊接的效果差异,本次模拟将文献[6]中单面爆炸焊接顶部设置的水层约束去除。图1(b)为单层爆炸焊接组结构图,其与图1(a)中的单面爆炸焊接之间仅存在炸药厚度的区别。2组实验基复板材料分别选用Q235钢和304不锈钢,具体尺寸见表1。炸药选用了密度0.8 g/cm3,爆速3 000 m/s的乳化炸药,2组实验中炸药层厚度分别设置为10 mm与16 mm。
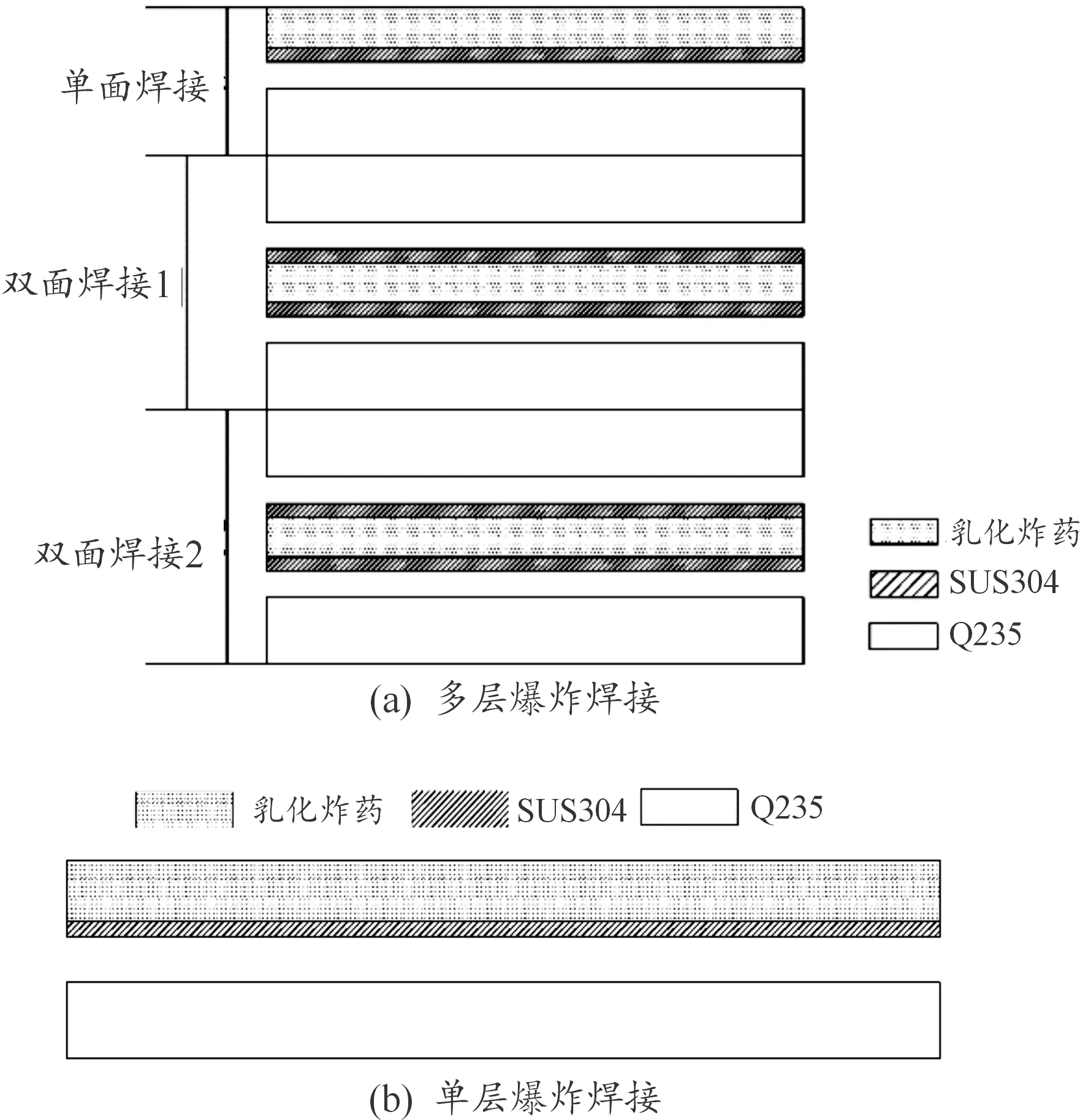
图1 计算模型示意图

表1 尺寸参数(mm)
2.2 材料参数与状态方程
选用JWL状态方程[7]及HIGH_EXPLOSIVE_BURN模型[8]对乳化炸药进行定义,其中JWL状态方程可用式(1)表达。式中:P为爆压,GPa;A,B,R1,R2,ω均为材料系数;V为爆轰产物的比容,无量纲;E0为炸药初始比内能,kJ/cm3。具体参数可见表2[9]。
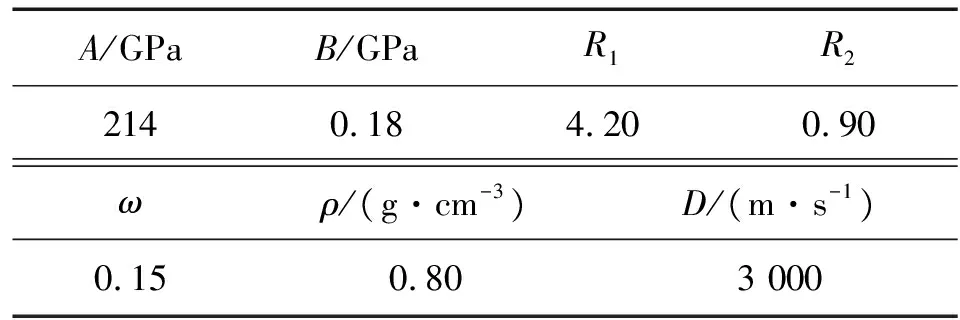
表2 乳化炸药的状态方程参数
(1)
与文献[6]中所选材料一致,基复板分别以密度为7.85 g/cm3和7.93 g/cm3的Q235钢和304不锈钢组成。爆炸焊接过程中基复板会在短时间内承受极强的冲击压力,因此选择常用于分析金属力学性能的Johnson-Cook模型[10]和Mie-Gruneisen状态方程[11]对基复材料进行定义。
Johnson-Cook模型在材料产生高速变形或高温软化(如弹道穿透和冲击、爆炸金属塑型)时仍然有效,以下式对其进行表述:
(2)
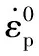
由于Johnson-Cook模型在与实体元素(solid elements)一起使用时需要为其添加状态方程,故选用能够精确计算高温高压下金属材料动态行为的Mie-Gruneisen状态方程。此状态方程可用于描述气体爆炸产物与高压固体之间的本构关系,具体可见式(3)。
(3)
式中:S1,S2,S3为方程拟合系数;γ0为Gruneisen系数;a为体积校正系数;C为材料声速;μ=ρ/ρ0-1,其中ρ和ρ0分别为材料当前密度与初始密度。基复板的材料模型具体参数与状态方程具体参数分别列入表3、表4中[9]。为佐证本次模拟中各材料选取参数的准确性,表5给出了前期实验所取材料特性参数,以作对比[6]。

表3 Q235钢与304不锈钢的Johnson-Cook材料模型参数

表4 Q235钢与304不锈钢的Gruneisen状态方程参数
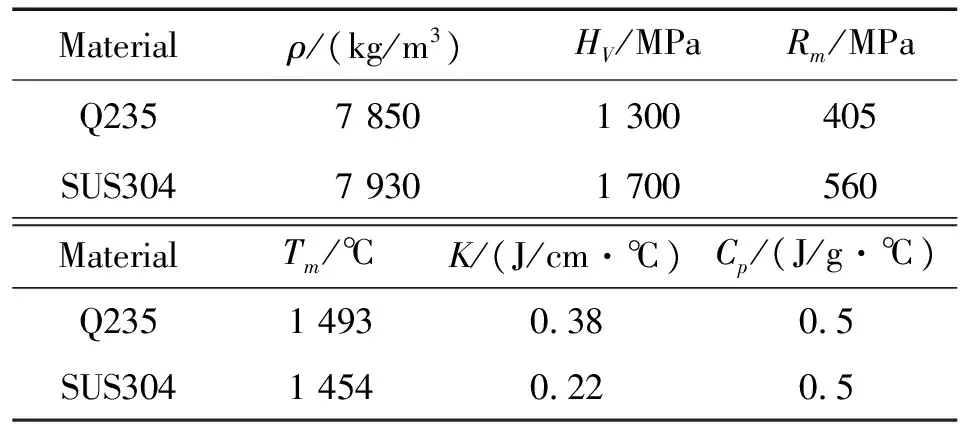
表5 Q235钢与304不锈钢的材料特性参数
3 三维模拟
光滑粒子流体动力学法(SPH)是模拟流体流动的一种无网格自适应拉格朗日粒子法。由于SPH法具有自适应、无网格和拉格朗日等特性,使得 SPH法非常适合用于处理高能炸药爆炸瞬间的大变形动力学问题[11]。在三维数值模拟问题中,由于SPH法需要建立的粒子数相较于一维与二维问题极大增加,导致整体计算效率低下。而传统的有限元法(FEM)虽然存在大变形、网格破碎等问题,但其在运算速度、模型建立等方面具有优势。包含了2种算法长处的SPH-FEM耦合法能够在提高计算效率的同时兼顾模拟质量,充分起到取长补短的效果[12]。
利用ANSYS19.0软件进行前处理,以SPH-FEM耦合算法为基础建立多层与单层爆炸焊接实验的三维模型,如图2所示。目标模型为横向多层重叠结构,建模顺序为基复板建模-炸药建模-网格划分-SPH化-设置接触。其中,单元类型选用SOLID164实体单元,各基复板均采用有限元网格划分,而炸药结构则利用LSPP软件进行SPH粒子化,光滑粒子大小Δr设定为0.1 cm,最后于K文件中设置SPH-FEM耦合接触。相较于全局使用有限元法或SPH法建模,SPH-FEM耦合法能在杜绝炸药网格大变形的同时兼顾效率,拥有较高的计算精度。

图2 三维建模示意图
3.1 碰撞速度
如图3所示,依据文献[6]中所设置的速度测点位置在2组实验的复板上分别选取特征点A~F,利用后处理软件LSPP记录并输出特征点的速度-时间分布情况见图4。
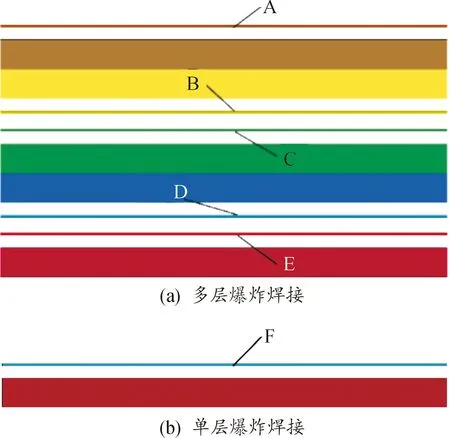
图3 特征点位置示意图
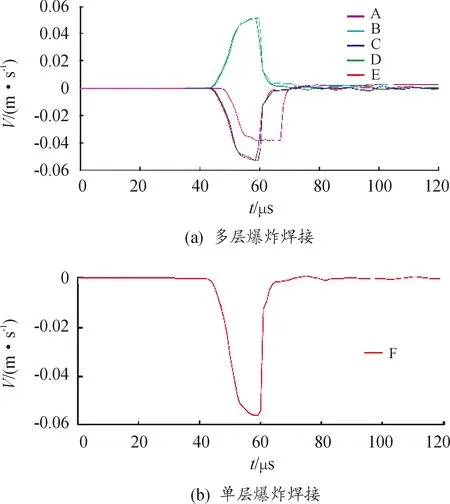
图4 特征单元A~F的速度-时间分布
各特征点的速度峰值依次为392 m/s、557 m/s、553 m/s、556 m/s、549 m/s、581 m/s,其中特征点B~F与文献[6]中利用电测法所获得的碰撞速度534 m/s和557 m/s误差为2.8%~4.3%,可认为该组模拟数据较为可靠。而特征点A与文献[6]给出的碰撞速度差异达到了惊人的26.6%,这是由于模拟中移除了原单面复合组顶端的水层约束,导致炸药的部分能量以冲击波的形式传递至空中,未能得到充分利用,证明了在炸药上部加装水层约束对提高炸药利用率具有一定效果[13]。位于双面焊接组上的特征点B~E与单层焊接实验中的特征点F之间碰撞速度的差异仅有4.1%~5.5%,说明双面爆炸焊接组与单层爆炸焊接实验取得了的近乎一致的效果。然而双面爆炸焊接组炸药厚度为10 mm,单层爆炸焊接实验炸药厚度却为16 mm,且综合考虑到双面爆炸焊接一次可以同时制备两块复合材料,计算出多层爆炸焊接比单层爆炸焊接提高了近68%的炸药利用率。
3.2 碰撞压力
作为爆炸焊接过程中的重要动态参数之一,碰撞压力代表了复板在飞行过程中由爆轰产物获得的能量大小,因此研究碰撞压力对分析基复板结合质量及能量分布有关键作用[14]。依靠基复板的材料声速及密度可以得到碰撞压力与碰撞速度的关系,如式(4)所示。
(4)
其中: vp为复板碰撞速度;vs,1,2为基复板材料声速;ρ1,2为基复板密度;P为碰撞压力[15]。文献[6]中通过电测法测得两组实验的碰撞速度为534m/s和557m/s,而Q235钢与304不锈钢的材料声速分别为4 569m/s和4 500m/s,则可通过式(4)得出两组实验中的碰撞压力计算值分别为P1=9.552GPa,P2=9.964GPa。
利用后处理软件输出图3中的特征点A~F的碰撞压力见图5。各特征点的碰撞压力峰值依次为6.46GPa、9.02GPa、9.62GPa、9.95GPa、9.14GPa、10.60GPa。与碰撞速度分布情况相似,由于移除了炸药顶端的水层约束,特征点A的碰撞压力与理论计算值P1之间也出现了较大差异。而碰撞压力反应了焊接过程中炸药传递至复板上的能量大小,这从另一方面再次证明了水层约束对炸药能量利用率的提升效果不容小觑[13]。特征点B~F的碰撞压力与理论计算值P1、P2的差别不大,总体误差范围在0.70%~6.38%,可信度较高。
通过图5能够发现,各组特征点在达到峰值压力前均出现了一种较弱的正向压力峰,整体压力分布呈现正向缓增长-负向快速下降-正向急速增长的趋势。以特征点F为例,导出其25~65μs之间的部分压力云图进行分析。如图6(a)(b)所示。
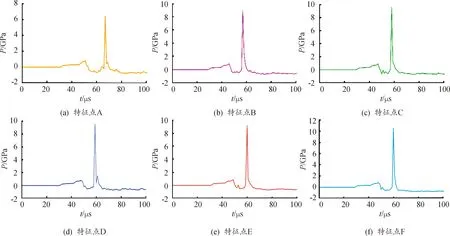
图5 特征单元A~F的碰撞压力-时间分布图

图6 不同时刻下特征单元F的碰撞压力云图
31 μs时特征点F的碰撞压力开始逐渐正向缓慢增加,直至44 μs时达到第一次峰值。这是由于前端基复板碰撞产生的振动波在复板中的传播速度与材料声速几乎相同,均为4 500 m/s,高于炸药的爆速3 000 m/s,因此特征点F至炸药激波阵面之间的待复合区域会持续受到前端基复板传递的振动波的叠加作用,使得特征点F所受的压力持续增加[16]。在48 μs时,爆轰波的激波阵面抵达特征点F,其所受压力开始负向下降;57 μs时,爆轰波的反应区整体越过特征点F,特征点上所受压力在缓慢下降中逐渐趋于稳定。这种快速下降—趋于稳定的短暂压力变化可通过爆轰波的ZND模型加以解释,图7为爆轰波传递过程的ZND模型[17],激波阵面的初始压力最高而炸药反应区的压力逐渐降低,在48~57 μs中炸药反应区越过特征点F并不断传递能量至复板上,因此作用于特征点F的压力得以短时间内快速负向下降;57 μs之后作用于特征点F上的仅有位于反应区后的压力较低的爆轰产物,因此特征点F上的压力开始在缓慢下降中趋于稳定。60 μs时特征点F于基板相撞并受到巨大冲击,致使其压力曲线短时间内急速正向增长;而62 μs时基复板已稳定复合,作用于特征点F上的压力也回归平稳。可以认为,特征点的压力分布趋势是在材料自身传递的振动波与炸药产生的爆轰波综合影响下形成的。
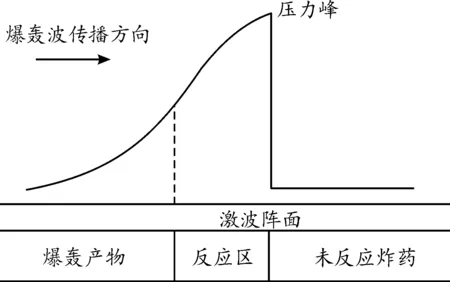
图7 爆轰波的ZND模型示意图
4 二维模拟
作为判断爆炸焊接质量的重要因素之一,金属结合面的波形分布情况能够充分反映基复板的结合强度[18]。以SPH-FEM耦合算法为基础的三维模拟虽然能够高效分析并输出各类动态参数,但却无法观察焊接过程中基复板结合界面的波形情况。为分析两组实验的焊接质量,建立整体SPH化的二维计算模型,如图8所示。二维模型中炸药及板材装配方式与三维建模一致,均采用横式铺设,起爆点及爆轰方向如图8(b)所示。二维建模与三维建模顺序基本一致,区别在于三维建模选取SOLID164三维实体单元而二维建模选用PLANT162平面实体单元。按由下至上的顺序依次构建基板、复板与炸药结构,对各部分统一进行网格划分及SPH化。基复板和炸药所取用的公式与材料参数均与三维建模相同,具体可见表2、3、4。图9、图10分别为第一组和第二组实验的模拟—实验波形对比图,由于双面焊接组合中两块复板所受的炸药荷载并无差别,因此仅取一块复合板进行界面波形分析。由图可见,各组复合板均成功复合,并未出现明显裂纹及等缺陷。单面组合由于卸除了炸药顶部的水层约束导致其基复板结合界面并未产生明显波形,而其余组合均获得了质量较高的波形结合面。各组模拟所得的波形结合面波高—波长比约为2∶5,与文献[6]中实验获得的波形尺寸近乎一致,验证了二维模拟的合理性。另外,双面组合1、2的模拟波形与单层焊接实验的模拟波形外观基本相同,说明了10 mm药厚的多层爆炸焊接可以实现16 mm药厚下单层爆炸焊接的效果,对于炸药药量的节省与生产效率的提高作用显著。
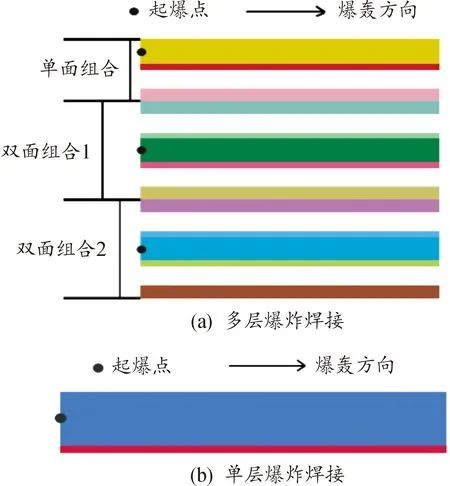
图8 二维建模示意图

图9 多层焊接实验复合界面波形对比

图10 单层焊接实验复合界面波形对比
5 结论
以ANSYS19.0软件为平台,综合了SPH-FEM耦合法与SPH算法,对Q235钢与304不锈钢的多层爆炸焊接实验分别进行了三维和二维数值模拟研究,对比分析了焊接过程中的动态参数及结合界面波形分布,主要结论有:
1)前期实验与数值模拟所获得的动态参数和界面波形均无较大差异,表明了基于SPH-FEM耦合法与SPH法的三维和二维数值模拟均能够对爆炸焊接过程进行有效还原。
2)计算了复板碰撞压力理论值,其与三维数值模拟所获得的动态参数基本吻合,通过分析振动波与爆轰波的传播规律解释了复板所受压力的特殊分布形态。
3)与传统单层爆炸焊接相比,多层爆炸焊接法能提高近68%的炸药利用率,且多层爆炸焊接可以在相同时间内制备多组复合材料,大大提高了生产效率。
