基于智能算法优化BP的航空器滑出时间预测
2023-02-11朱晓波贾鑫磊王楚皓
朱晓波, 贾鑫磊, 王楚皓
(中国民用航空飞行学院空中交通管理学院, 广汉 618307)
滑出时间是评估大型机场场面运行效率的主要性能指标,指的是离港航空器的起飞时刻与推出开车时刻之间的时间间隔[1]。目前,大型枢纽机场的航空器平均滑出时间已超过25 min。多数机场仍采用基于经验的滑出时间来对航空器的推出开车、滑行进行指挥,但在机场场面交通流、滑行距离、场面运行模式等诸多因素的共同影响下,常产生推出开车后原地等待或滑行过程中等待现象,致使实际滑出时间与经验滑出时间差异较大,影响机场运行效率和安全性。因此,科学准确地预测离港航空器的滑出时间,对于提升机场场面运行效率和协调决策能力,降低运行成本和污染排放至关重要。
国外关于滑出时间预测的研究始于21世纪初,基于起飞队列长度、跑道、机型等因素构建了滑出时间的多元线性回归预测模型。Balakrishna等[1]基于随机动态规划理论建立了多跑道非参数强化学习滑出时间模型。Lee等[2]构建了滑出时间的快速仿真预测模型,比较了多种机器学习算法的性能。Elizabeth等[3]基于航空器历史数据对离港航空器的滑出时间进行了动态预测,提出了基于强化学习的Q-Learning方法。Murca等[4]提出了考虑6个影响因素的滑出时间预测模型。Herrema等[5]基于历史数据对单跑道场面滑行时间进行了预测。
国内滑出时间预测相关研究起步较晚。冯霞等[6]基于单跑道建立了无障碍滑出时间的计算模型与基于排队论的等待起飞时间预测模型。刘继新等[7]提出了基于支持向量回归(support vector regression, SVR)和反向传播(back propagation,BP)神经网络的离港滑行时间预测模型。邢志伟等[8]利用贝叶斯网的增量学习特点对预测模型进行动态调整,从而使模型能够动态地估计离港航空器滑行时间。Lian等[9]提出了基于滑出时间预测的航空器动态推出控制策略,旨在减少然后消耗和污染排放。Li等[10]运用深度学习算法预测离港航空器的滑出时间,并比较了多种算法的优劣。黄龙杨等[11-12]讨论了离港航班滑出时间的预测及其应用,并基于SSA-BP模型对离港航班的滑出时间进行了预测。
综上所述,现有研究成果分析了离港航空器滑出时间主要影响因素,预测方法大致可分为3类:基于排队论的滑出时间预测方法;基于快速仿真的滑出时间预测方法;基于历史数据挖掘的滑出时间预测方法。但是,现有研究成果多以单跑道或多跑道中的某一条跑道作为研究对象,国外交叉跑道滑出时间研究成果也不能直接使用;研究方法对初始值权值和阈值较为敏感,预测结果的准确性和稳定性有待进一步提高。因此,现以典型的H形双跑道机场为研究对象,构建基于相关性分析的滑出时间BP预测模型,并采用粒子群优化(particle swarm optimization,PSO)算法和麻雀搜索算法(sparrow search algorithm,SSA)获取BP神经网络的最优权值和阈值,以期提升离港航空器滑出时间的预测精度。
1 基于相关性分析的滑出时间预测模型构建
通过文献追踪可知,离港航空器的滑出时间影响因素较多,受机场场面交通流的影响,航空器之间会争夺跑道、滑行道资源,这必然会导致某航空器的等待,从而使得它的滑出时间与其无障碍滑出时间有较大的偏差。同时,滑出时间还受到流量控制、恶劣天气、跑道运行模式、机型、转弯数量等因素的影响,但是这些因素或不可量化,或影响较小,故不予考虑。因此,离港航空器滑出时间的主要可量化因素包括:同时段滑行的起飞航空器数量、同时段滑行的落地航空器数量、起飞队列长度、半小时平均滑出时间、滑行距离和滑行过程中经过的热点数量6种。
1.1 参数定义
(1)离港航空器滑出时间(taxi-out time, TOT)等于该航空器离港实际起飞时间(actual take off time, ATOT)与实际撤轮档时间(actual off block time, AOBT)之间的差值。
TOT=ATOT-AOBT
(1)
(2)同时段滑行的离港航空器数量x1(架次)。
(2)
式(2)表示航空器j的实际起飞时间tATOTj刚好落在航空器i的实际推出开车时间tAOBTi和实际起飞时间tATOTi之间的所有离港航空器数量。
(3)同时段滑行的进港航空器数量x2(架次)。
x2,tAOBTi (3) 式(3)表示航空器j的实际落地时间tALDTj刚好落在航空器i的实际推出开车时间tAOBTi和实际起飞时间tATOTi之间的所有离港航空器数量。 (4)起飞队列长度x3(架次)。起飞队列中包含两种类型的航空器d1和d2。 (4) 式(4)中:d1表示航空器j的实际推出开车时间tAOBTj比航空器i的实际推出开车时间tAOBTi早;且航空器j的实际起飞时间tATOTj比航空器i的实际起飞时间tATOTi晚,但比航空器i的实际起飞时间tATOTi早。d2表示航空器j的实际推出开车时间tAOBTj比航空器i的实际推出开车时间tAOBTi晚,且比航空器i的实际起飞时间tATOTi早,且航空器j的实际起飞时间tATOTj比航空器i的实际推出开车时间tAOBTi晚,但比航空器i的实际起飞时间tATOTi早。 (5)以半小时为时间片的平均滑出时间x4(s)。 (5) 式(5)中:ti为第i架离港航空器的滑出时间;n为半小时中滑出的离港航空器数量。 (6)离港航空器滑行距离x5(m)。 (6) 式(6)中:da,i为航空器i滑行路径的测量长度;db为跑道的测量长度;3 600为跑道长度。 (7)滑行过程中经过的冲突热点区域(hotspot, HS)数量x6(个)。 航空器在滑行过程中通过冲突热点区域时,通常会减速慢行,或等待冲突解脱从而增加滑行时间。因此,离港航空器的标准滑行路径中经过的热点区域个数越多,滑行时间越长。 所用数据来源于中南某枢纽机场2018年8月6—19日共计2周的实际运行数据,数据集共有记录12 923条,包含离港航空器6 352架次和进港航空器6 571架次;每条记录由飞机呼号、机型、实际起飞时间、实际撤轮档时间、实际落地时间、跑道号、停机位等关键信息组成。通过对数据整理,删除重复及异常数据,并根据式(2)~式(6)依次得到同时段滑行的离港航空器数量、同时段滑行的进港航空器数量、起飞队列长度、半小时平均滑出时间、滑行距离、经过的冲突热点数量以及实际滑出时间。通过对样本数据进行相关性分析可得图1。 图1(a)、图1(b)分析了滑出时间与同时段滑行的离港航空器数量和进港航空器数量的相关性,相关系数r=0.607 7和r=0.551 9,表明滑出时间与同时段滑行的离港航空器数量强相关(r>0.6),与同时段滑行的进港航空器数量中度相关(0.3 图1 离港航空器滑出时间影响因素相关性分析Fig.1 Correlation analysis of influencing factors of aircraft taxi-out time BP神经网络是目前使用最广泛的神经网络结构,具有任意复杂的模式分类和多维函数映射能力,被广泛应用于模式识别、分类、预测等领域[12]。为进一步分析讨论不同相关性的影响因素对滑出时间的影响程度,构建了基于相关性分析结果的离港航空器滑出时间预测模型,模型的输入分为3种情况,如表1所示。 表1 BP神经网络输入分类Table 1 input classification of BP neural network 其中,3元组合预测模型仅考虑强相关的影响因素对滑出时间的影响;4元组合预测模型仅考虑强相关和中度相关的影响因素;6元组合预测模型将综合考虑所有的可量化影响因素。 研究对象是中国中南某枢纽机场,东跑道3 400×45 m,西跑道3 800×60 m,东西跑道之间间距约为1 590 m,可根据交通流情况选择隔离运行模式或者相关平行进近模式,该机场共有9个冲突热点(HS1~HS9)。通过对数据整理,删除重复及异常数据,并根据式(2)~式(6)依次得到同时段滑行的离港航空器数量、同时段滑行的进港航空器数量、同时段推出的离港航空器数量、半小时平均滑出时间、滑行距离、滑行过程中经过的冲突热点区域数量、实际滑出时间,最终得到样本数据6 200条,如表2所示。 表2 样本数据Table 2 sample data 基于MATLAB中的神经网络工具箱进行编程,载入所有样本数据,并将其进行归一化处理;设置最大迭代次数1 000次,学习率为0.01,目标收敛误差为0.001,网络的隐层节点数设置为10个。将样本数据进行按照8∶2的比例划分为训练集和测试集,并对训练集数据进行训练,更新权重值和阈值直到网络趋于稳定。然后,随机从测试集中随机选择100个数据,代入训练后的神经网络进行预测,并将结果进行反归一化,得到预测结果及误差分布情况对比如图2和表3所示。 图2 基于BP神经网络的滑出时间预测结果对比Fig.2 Comparison of taxi-out time prediction results based on BP neural network 表3 滑出时间预测结果误差分布对比Table 3 Comparison of error distribution of taxi-out time prediction results 可见,3种预测模型均能实现对离港航空器滑出时间的有效预测,4元组合预测模型的效果最佳。其中,3元组合预测模型的曲线拟合优度R2=0.891 0,模型中仅考虑了强相关的场面交通流,而未考虑进港航班对滑出时间的影响,因此预测结果与真实值偏差稍大。4元组合预测模型的曲线拟合优度高达R2=0.925 8,该模型综合考虑了地面的瞬时交通流,起飞队列,平均滑出时间等多种主要因素,因此预测结果与真实结果之间的偏差最小。6元组合预测模型的曲线拟合程度为R2=0.900 3,较4元组合预测预测模型拟合程度反而降低了,说明弱相关性的滑行距离和滑行过程中经过的冲突热点区域个数引入后对滑出时间预测结果是不利的。 基于预测结果的误差分布范围、平均绝对误差百分比(mean absolute percentage error,MAPE)、平均绝对误差(mean absolute error,MAE)、均方根误差(root mean squared error,RMSE)对模型进行评价,结果如表3所示。考虑强相关和中度相关影响因素的4元组合预测模型的预测结果误差最小,误差范围在±300 s以内占比92%,MAPE为14.22%,MAE为110.24 s,RMSE为114.03 s。综合考虑强相关、中度相关和弱相关影响因素的6元组合预测结果精度较3元组合预测模型高,较4元组合预测模型低,进一步说明了弱相关影响因素的引入会影响模型预测的准确率。通过对现有研究成果的分析,基于排队论的滑出时间预测模型的精度大约为78%,而基于机器学习的滑出时间预测模型可达到82%左右,所提出的考虑可量化因素的滑出时间预测模型的平均预测精度可达到85%,说明预测结果是可信的。但是,预测结果对BP神经网络的初始权值和阈值敏感,模型输出的准确性和稳定性不甚理想。 粒子群算法(PSO)是一种通过群体中个体间的协作和信息共享获得最优解的方法,广泛应用于函数优化、模糊系统控制、数据挖掘等领域。粒子群算法的特点是原理简单、容易实现且可调节的参数较少,属于随机搜索的全局优化方法。 针对传统BP神经网络在离港航空器滑出时间预测时存在对初始权值和阈值敏感、准确性和稳定性不好等缺点,利用粒子群算法的全局搜索能力来优化神经网络的拓扑结构、链接权值和阈值,将粒子群算法良好的全局寻优能力与BP神经网络良好的局部寻优能力相结合,以提高神经网络的泛化能力和学习性能,从而改进神经网络的整体搜索效率。基于PSO-BP的滑出时间预测流程图如图3所示。 图3 基于PSO-BP的滑出时间预测流程图Fig.3 Flow chart of estimated taxi-out time prediction based on PSO-BP 首先从Excel中读取样本数据,确定网络的输入输出,按比例8∶2划分训练集和测试集并将数据进行归一化处理;然后确定网络的拓扑结构以及PSO算法的种群规模、维度等参数;并随机初始化粒子的位置和速度,计算各个体的适应度值,并求解个体和群体的最佳适应度值,更新粒子的位置和速度直到获得全局最佳位置。最后,将该位置信息赋值给BP神经网络的权值和阈值,并对PSO优化后的BP神经网络进行训练与仿真预测。 麻雀搜索算法(SSA)是一种基于麻雀的觅食行为和反捕食行为的群体优化算法,其基本原理如下。 (1)发现者通常有较高的能量储备,负责搜索到具有丰富食物的区域,为加入者提供觅食的区域和方向。 (2)一旦麻雀发现了捕食者,发出鸣叫作为报警信号;当报警值大于安全值时,发现者将加入者带到其他安全区域觅食。 (3)发现者和加入者身份动态变化,但是各自所占种群数量的比重不变。 (4)加入者的能量越低,则其所处的觅食位置就越差。 (5)觅食过程中,加入者总能搜索到提供最好食物的发现者,并在其周围觅食。 (6)当意识到危险时,群体边缘的麻雀会迅速向安全区域移动,以获得更好的位置,位于种群中间的麻雀则会随机走动,以靠近其他麻雀。 针对传统BP神经网络在离港航空器滑出时间预测时存在对初始权值和阈值敏感、准确性和稳定性不好等缺点,利用麻雀搜索算法的觅食和反捕食行为不断更新种群的适应度和最优位置,从而获取BP神经网络的最优权值和阈值参数,然后再进行训练和仿真预测,其算法流程图如图4所示。 图4 基于SSA-BP的滑出时间预测流程图Fig.4 Flow chart of taxi-out time prediction based on SSA-BP 首先,选取训练集与测试集整体的均方误差作为适应度,适应度函数越小,表示训练越准确,且兼顾模型的预测精度更好。从Excel中读取样本数据,确定网络的输入输出,按比例8∶2划分训练集和测试集并进行归一化处理;然后确定网络的拓扑结构,随机初始化网络的权值、阈值,麻雀种群规模、最大迭代次数、捕食者和发现者的比例等参数,以均方误差最小值作为最优适应度,将优化后麻雀位置信息作为权值与阈值赋给BP,并对SSA优化后的BP神经网络进行训练与仿真预测。 基于MATLAB中的神经网络工具箱进行编程,设置BP神经网络最大迭代次数10 000次,学习率为0.001,目标收敛误差为0.001。设置粒子群算法的初始种群规模为50,最大迭代次数200。设置麻雀初始种群大小为50,最大迭代次数200,发现者和加入者占种群的比重均为0.5,能意识到有危险的麻雀占种群的比重为0.2。将训练集数据进行训练,然后从测试集中随机抽样200个数据进行测试,经PSO和SSA优化前后的BP神经网络预测值与真实值的对比分别如图5(a)和图5(b)所示。 图5 PSO-BP和SSA-BP预测结果对比Fig.5 Comparison of prediction results between PSO-BP and SSA-BP 可见,BP、PSO-BP、SSA-BP均能实现对离港航空器滑出时间的有效预测。但是,基于BP神经网络的滑出时间预测结果对初始权值和阈值敏感,准确性和稳定性不好有待进一步的提高。因此,使用PSO和SSA两种智能优化算法分别获得BP神经网络的最优权值和阈值参数,最终获得的预测结果更接近于真实值,且误差分布更集中、更均匀。同时,从表4可以看出,基于PSO优化后的BP神经网络预测结果误差在±60 s内的准确率提升了14%,误差±180 s内的准确率提升了10%,误差±300 s内的准确率提升了4%。基于SSA优化后的BP神经网络预测结果误差在±60 s内的准确率提升了20%,误差±180 s内的准确率提升了12%,误差±300 s内的准确率提升了6%。以上指标充分说明了SSA算法比PSO算法对模型的优化力度更强。 表4 滑出时间预测结果误差分布对比Table 4 Comparison of error distribution of taxi-out time prediction results 为进一步对基于PSO和SSA优化后的BP神经网络预测结果进行科学评价,以平均绝对误差百分比(MAPE)、平均绝对误差(MAE)、均方根误差(RMSE)来进行验证,结果如表5所示。 表5 离港航空器滑出时间预测精度评价Table 5 Prediction accuracy evaluation of departure flight taxi-out time 可见,基于PSO优化后的BP神经网络预测结果较优化前的MAPE提升了1.13%,MAE减少了4.48 s,RMSE减少了4.67 s;基于SSA优化后的BP神经网络预测结果较优化前的MAPE提升了3.05%,MAE减少了16.55 s,RMSE减少了14.31 s。以上数据充分说明了智能优化算法能有效获取神经网络的局部最优权重和阈值,能有效地提升离港航空器滑出时间预测结果的精度,且麻雀搜索算法比粒子群算法对模型的优化效果更好。经过智能优化算法优化BP后的滑出时间预测结果精度可提升约5%,误差±300 s内的准确率提升至98%,且误差分布也越来越均匀,从而验证了智能优化算法的有效性。 众所周知,优化算法往往在提升预测结果精度的同时会增加运算时间,对算法的时间效率进行对比分析,结果如表6所示。 表6 算法的时间效率分析Table 6 Time efficiency analysis of algorithm 可见,为了获得更高的精度,运算时间的增加是必然的,且优化力度更强的SSA算法比PSO算法所需时间也更长。 (1)离港航空器滑出时间与半小时平均滑出时间、起飞队列长度、同时段滑行的离港航空器数量均有强相关性,与同时段滑入航空器数量中度相关,与滑行距离和滑行过程中经过冲突热点区域数量相关性较弱。 (2)考虑强相关和中度相关可量化影响因素的4元组合预测模型的滑出时间预测结果精度最高;引入弱相关的滑出距离和转弯个数后,模型的预测结果精度有所降低。 (3)智能优化算法通过获取神经网络的局部最优权重和阈值,可有效地提升离港航空器滑出时间预测结果的精度,且麻雀搜索算法比粒子群算法对模型的优化效果更好,但是运算过程耗时更长。 (4)下一步的工作重点将放在基于滑出时间预测的离港航空器推出及滑行控制策略研究方面。1.2 相关性分析
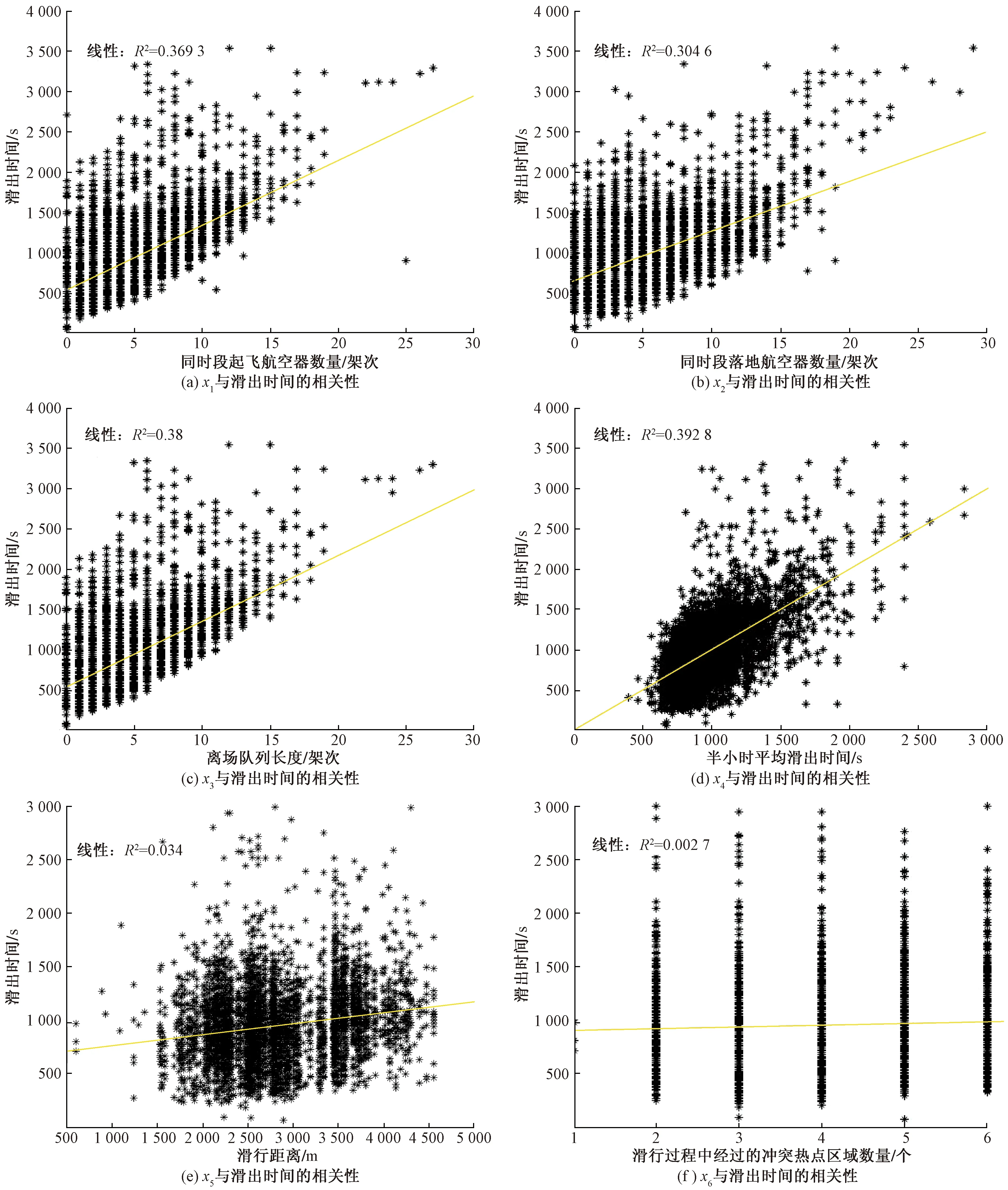
1.3 模型构建

2 基于BP神经网络的离港航空器滑出时间预测
2.1 数据来源及预处理

2.2 滑出时间预测结果及分析
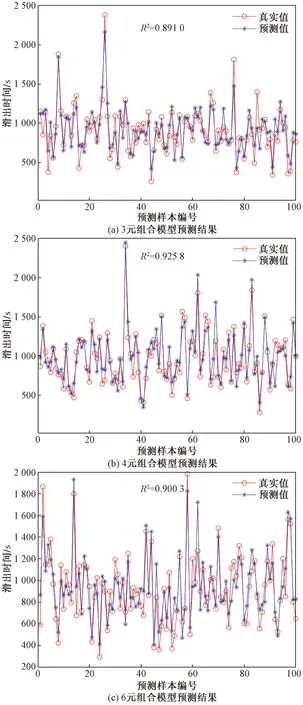
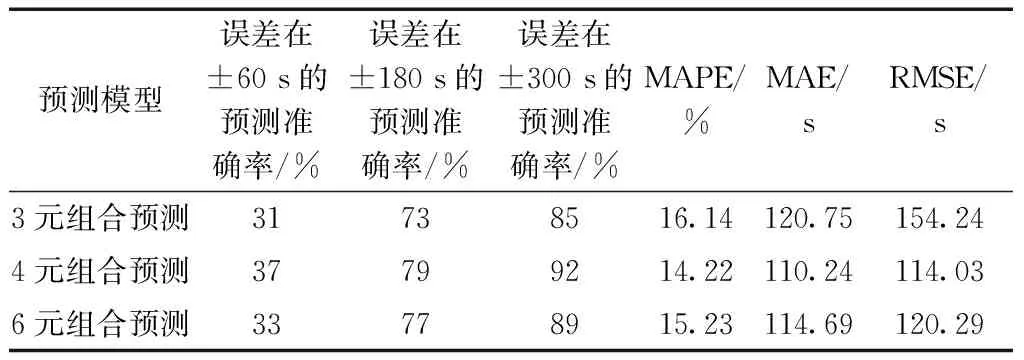
3 基于智能算法优化BP的滑出时间预测模型
3.1 基于PSO-BP的滑出时间预测模型

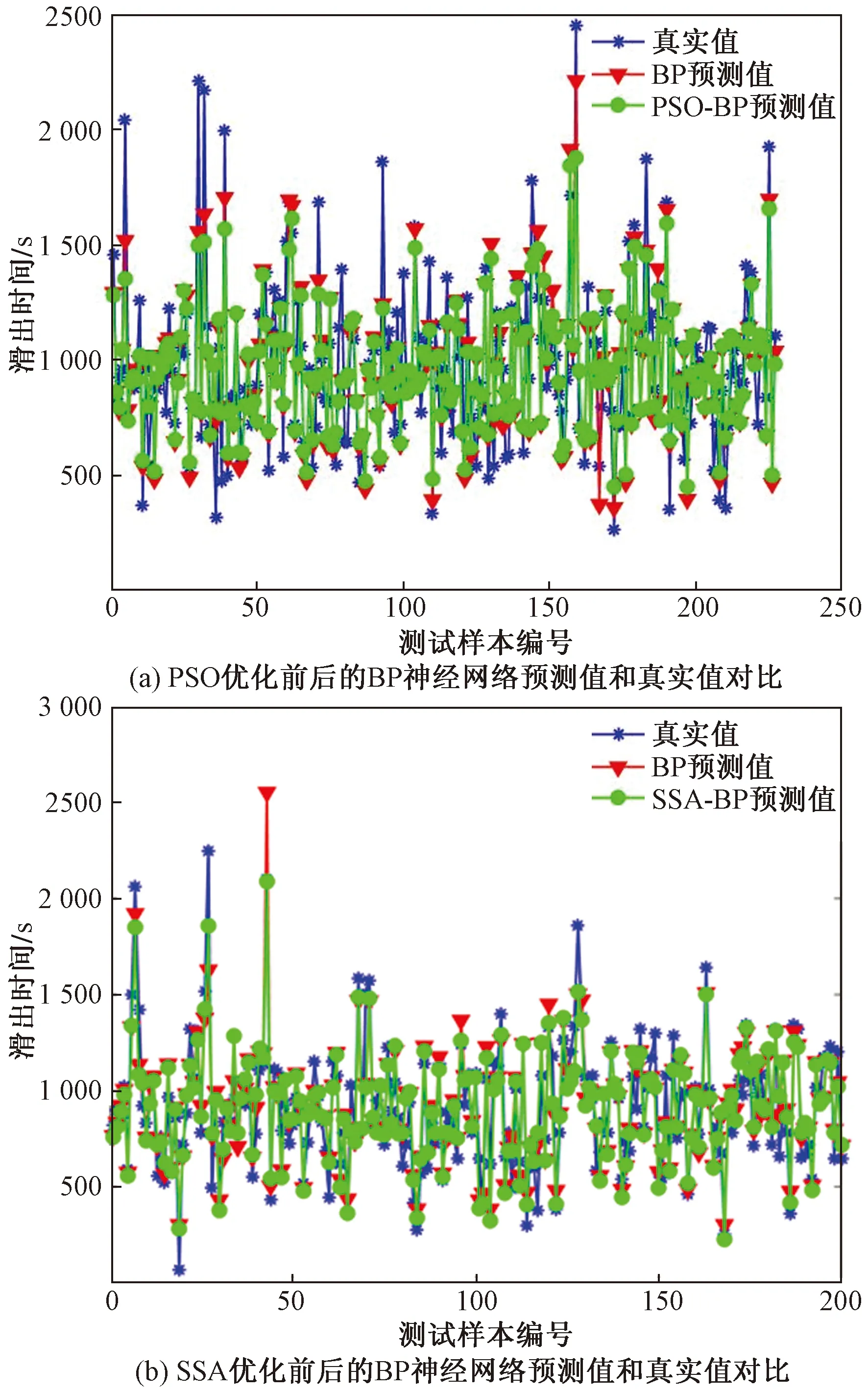
3.2 基于SSA-BP的滑出时间预测模型
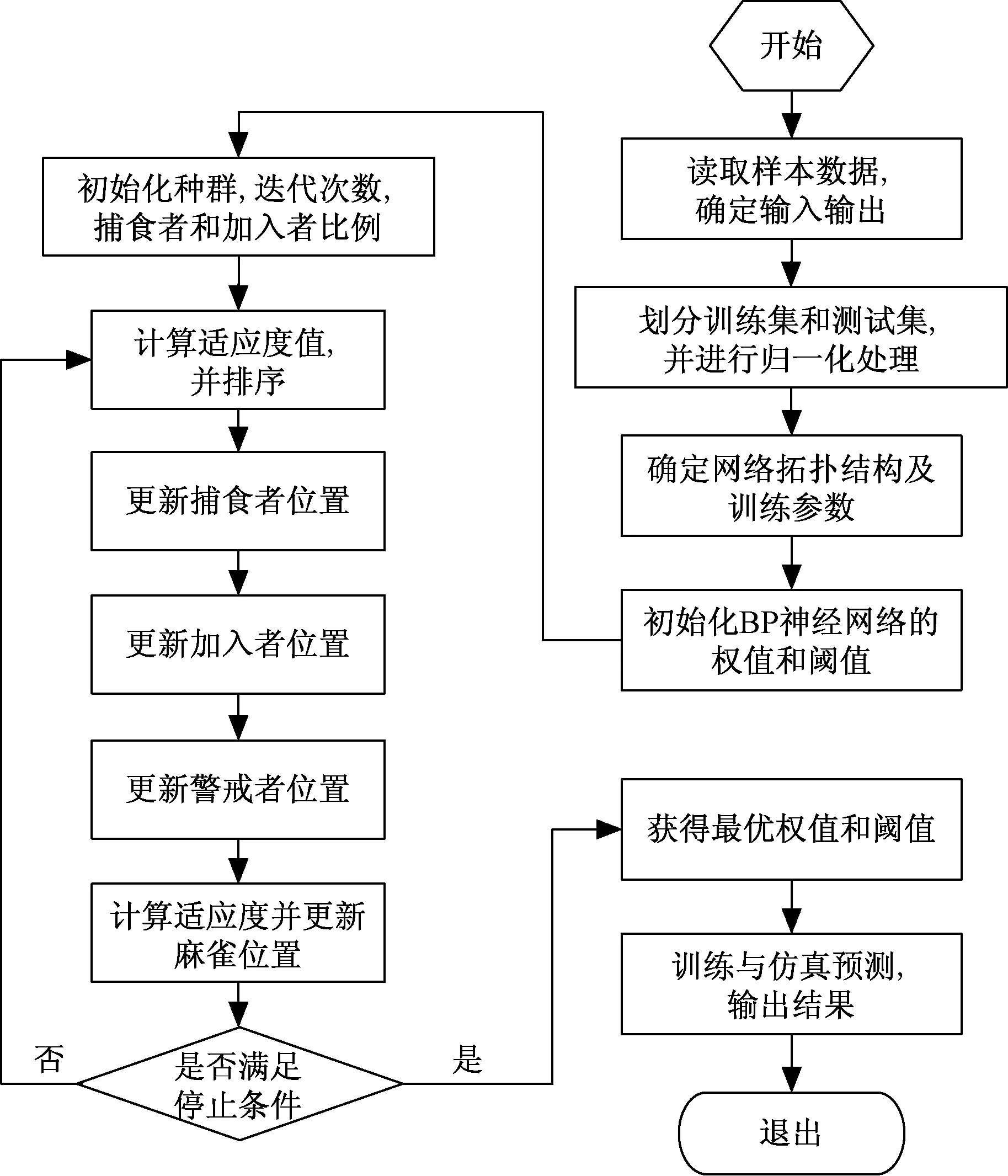
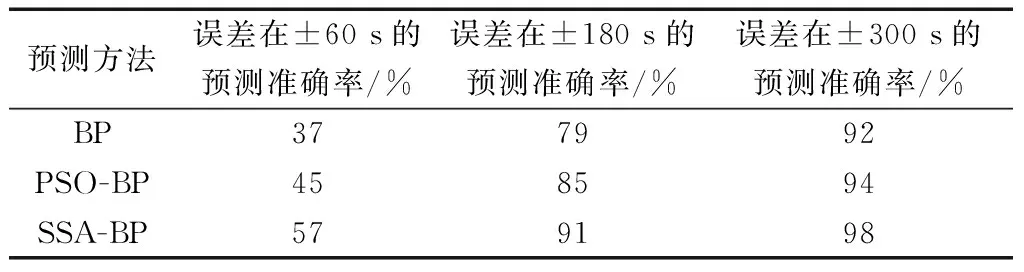
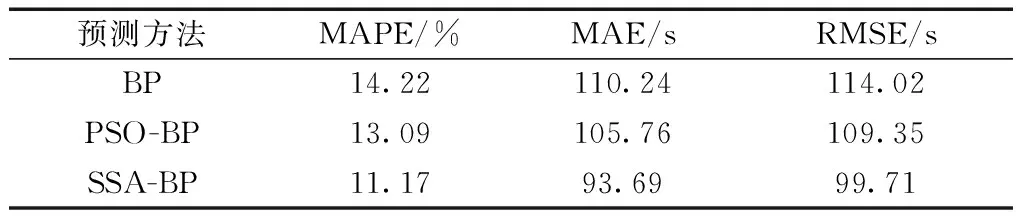
3.3 滑出时间预测结果分析和讨论

4 结论
