基于两级信息融合的隧道掘进机拆装装置作业安全预警模型

安小宇， 王德健， 李楠， 李刚， 时安琪， 杨洋， 陈傲松

(1.郑州轻工业大学电气信息工程学院， 郑州 450002； 2.中铁工程装备集团盾构制造有限公司， 郑州 450016)

隧道掘进机(tunnel boring machine，TBM)的拆装维修一般采用开挖竖井或者洞内大面积扩容的方法来实现，其工程量巨大，造价高，还需要土方回填处理，工程周期长，循环经济性差。目前，直接针对洞内TBM快速拆装装置的研发在国内外尚属空白。

TBM拆装装置属于大型起重设备，装置在进行作业时需要缓慢地进行升降吊装，其工作时间较长。而且作业过程中需要根据现场实际情况灵活调整工作模式，不同的工作时间段其工况参数的要求也不同。同时洞内空间有限、吊装主机吨位大等致使装置在作业时操作难度大、危险性高，具有极高的安全隐患，为保证拆装装置的作业安全，需要根据TBM拆装装置的结构特点和工艺要求对装置作业时的安全状况进行有效预警。

目前，国内外针对大型起重、吊装设备上的安全预警模型已有一定数量的研究成果，如杨斌等[1]通过建立灰色综合预测模型，结合归一化数据处理的不同退化特征值，以实现起重机的安全预警；刘名强等[2]通过粗糙集(rough set，RS)属性约简算法确定模型安全预警因子，选用混合核函数构建关联向量机(relevance vector machine，RVM)预警模型，并通过改进粒子群算法(improved particle swarm optimization，IPSO)寻优确定核参数，建立装配式吊装作业预警模型；Ren等[3]通过对起重机运动和位置的实时监测，以实时对象数据建立加权线性回归模型对起重机安全进行预测；随着人因失误问题的凸显，马辉等[4]通过分析施工现场人、物以及环境及这3类危险源交叉关联的情境，建立基于支持向量机(support vector machine，SVM)分类算法的空间单元安全预警模型；Shin[5]将塔机作业安全性研究的重点逐步从塔机本质安全与作业监测转向人为因素方面进行分析；郑霞忠等[6]运用模糊数学，结合认知可靠性与失误分析方法(cognitive reliability and error analysis methods，CREAM)构建塔机作业人因可靠性分析模型，以提高塔式起重机作业的可靠性。

综上所述，目前针对大型起重设备的安全预警研究成果相对有限，但国内外还没有见诸TBM拆装装置安全作业预警模型的研究成果。因此现依托郑州市重大专项“隧道掘进机(TBM)主机洞内快速拆装400 t群控液压举撑转运变位系统研制”对拆装作业过程中的安全预警模型进行研究。结合装置本身特点，使用TBM拆装装置上的拉力传感器采集的两组钢丝绳拉力数据、压力传感器采集的四组液压缸压力数据、偏载传感器采集的一组偏载角数据、位移传感器采集的一组拆装装置起升高度数据，以此8类数据作为基础，建立两级信息融合安全预警模型。一级融合将前期采集的8类数据进行预处理，包括判断错误数据和归一化处理，之后将8类数据通过层次分析法-熵权法算法融合得出安全状态系数，安全状态系数可以对比拆装装置的作业警度与风险等级，以得到此时拆装装置的安全状态。二级融合是将一级融合得出的安全状态系数作为输入，分别建立灰色模型(grey model，GM)、差分自回归移动平均(autoregressive integrated moving average model，ARIMA)、长短期记忆网络(long short-term memory，LSTM)3个单项预测模型，对后期拆装装置的安全状态系数进行预测，同时根据单项预测模型建立基于简单平均原理的简单平均组合模型[7]和基于最小误差平方与最小二乘法的最优加权组合模型[8]，通过三类模型所预测的安全状态系数与真实值之间的比较，选出预测效果最好的安全预警模型。之后将一级融合与二级融合进行结合，建立两级信息融合的TBM主机拆装装置安全作业的预警模型。

1 融合算法与安全状态系数

1.1 层次分析法计算过程

层次分析法[9]是将各项指标进行比较，两个指标间的重要程度通过尺度表来确定，尺度表如表1所示。

表1 1～9尺度表

根据尺度表打分规则，邀请大学教授、中铁装备以及新乡江河起重机相关起重专家共10余人对安全预警各指标进行评定打分，打分结果相同的进行采纳，结果不同的根据各个专家协商后的结果为准，以此建立判断矩阵A。通过协商最后确定相同指标其尺度相同；拉力指标比压力指标与偏载角指标稍显重要，比起升高度指标十分重要；压力指标比偏载角指标稍显重要，比起升高度指标明显重要；偏载角指标比起升高度指标明显重要。通过上述打分结果即可建立判断矩阵A。

(1)判断矩阵A及权重向量计算公式。

(1)

(2)

(3)

(4)

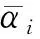
(2)检验判断矩阵A一致性。

(5)

(6)

式中：CI为判断矩阵一致性指标；RI为随机一致性指标，其值与判断矩阵的阶数有关；CR为一致性比率，当CR<0.1时，判断矩阵满足一致性检验；当CR>0.1时，需重新对安全预警各指标打分，直至CR<0.1。

1.2 熵权法计算过程

熵权法[10]是根据指标的变异性来最终确定各评估指标的权重[11]，其计算过程如下。

(1)数据标准化处理。

(7)

式(7)中：xij为原始数据i指标的第j个值；xmin为TBM拆装装置空载时i指标的最小值；xmax为i指标的最大值，例如4个压力指标，其xmin为2.84 MPa，xmax为19.66 MPa。

(2)计算i指标的熵值。

(8)

(9)

式中：ri为i指标的比重；ei为i指标熵值。

(3)计算i指标的熵权βi。

(10)

1.3 融合算法

采用层次分析法与熵权法相结合的融合算法，可以得到更加科学准确的指标权重值[12]。组合权重的常用方法有乘法归一法和平均值法，由于乘法归一法存在权重含义模糊的缺点，可能导致权重极端化。因此为保证主观与客观的兼容性，避免权重极端化的发生，采用平均值法确定指标综合权重。

(11)

式(11)中：ωi为i指标通过平均值法得到的综合权重；αi为层次分析法得到的权重；βi为熵权法得到的权重。

根据矩阵A可以计算出层次分析法中各个指标的权重，通过TBM拆装装置所装传感器采集的54组共432个数据可以计算得出熵权法中各个指标的权重。融合算法所得的8个指标的权重分配如表2所示。

表2 各指标权重分配Table 2 Weight distribution of each indicator

1.4 安全状态系数

首先将8类原始数据进行归一化处理，归一化处理就是将数据如同式(7)一样进行标准化处理，将经过归一化处理的某时刻指标数据分别与对应的融合算法确定的权重结合，将结合后的数据相加便得到了这一时刻的安全状态系数，安全状态系数的值的范围在0～1，同时可以将此时刻的安全状态系数与TBM拆装装置作业警度与风险等级进行对比，以此判断此时TBM拆装装置作业是否安全。而拆装装置作业的警度分为无警与报警，风险等级分为安全、相对安全和不安全3个等级，具体划分标准如表3所示。

表3 警度与风险等级划分标准Table 3 Criteria for classification of warning degree and risk level

2 建立预测模型

2.1 灰色预测模型

灰色模型(GM)是最基本的灰色系统理论模型，其建模过程[13-14]如下。

(1)对原始数据序列x(0)进行一次累加计算，得到有规律的数据序列x(1)。

(5)模型精度检验。

2.2 ARIMA模型

ARIMA(p，d，q)模型又称差分自回归移动平均模型，通过线性自动回归、移动平均和差分计算3种变量进行构建，对平稳时间序列进行定阶和参数估计，运用信息准则法选择合适参数[15]。

ARIMA模型[16-17]可通过差分原则将非平稳原始序列转变为平稳序列，通过建立自相关与偏自相关图对模型进行定阶，即确定p、d、q的值。根据所选择参数建立预测模型，根据拟合效果选出最优预测模型，并进行后期数据预测。

2.3 LSTM模型

LSTM是循环神经网络(recurrent neural network，RNN)的一种变体结构，其信息流传通过3个逻辑门(遗忘门、输入门、输出门)控制[18]。LSTM细胞单元结构如图1所示。

xt为细胞单元输入的偏置参数；ct-1为上一细胞状态；ht-1为上一细胞隐藏状态向量；ct为单元状态；ht为隐藏状态权重；ft为遗忘门权重；it为输入门权重；zt为细胞状态权重；ot为输出门权重[19]图1 LSTM细胞单元结构Fig.1 LSTM cell unit structure

2.4 组合预测模型

则第t时刻组合预测模型的预测值vt为

vt=k1v1t+k2v2t+k3v3t

(12)

使用组合模型是为了减少预测值与真实值之间的误差平方和，那么最优组合模型权重分配问题就转化为最小误差平方和最小二乘法的数学规划问题，即

(13)

式(13)中：J为组合模型预测值与真实值的误差平方和；Kn为组合模型的权重系数向量；E(n)为组合模型预测值与真实值的误差信息矩阵；Rn为n×1 的列阵。对式(13)进行拉格朗日乘子法求解得

(14)

结合式(13)与式(14)可得组合模型最小误差平方和为

(15)

2.5 模型比较

最优预测模型是通过单项模型与组合模型的预测值与真实值之间的相关系数R、平均绝对误差(mean absolute error，MAE)、平均相对误差(mean absolute percentage error，MAPE)、均方根误差(root mean square error，RMSE)4个指标和后期相对误差决定的，4个指标及其表达式如下。

(1)相关系数(R)。表达式为

(16)

(2)平均绝对误差(MAE)。表达式为

(17)

(3)平均相对误差(MAPE)。表达式为

(18)

(4)均方根误差(RMSE)。表达式为

(19)

3 实例分析

3.1 数据来源与信息融合

根据TBM拆装装置吊装TBM主机时一段时间内所采集的2组钢丝绳拉力数据、4组液压缸压力数据、1组偏载角数据、1组装置起升高度数据共8类84组672个数据作为基础，以前面54组共432个数据作为训练样本，以后期30组共240个数据作为检验样本。首先进行一级融合，将8类数据进行归一化处理，将归一化处理后的8类数据与对应层次分析法-熵权法融合算法所得权重融合得出安全状态系数，安全状态系数可以对比拆装装置的作业安全等级，以得到此时拆装装置的安全状态。将融合得出的前54个安全状态系数作为二级融合输入，根据所得的安全状态系数数据，ARIMA模型参数为p=1，d=2，q=1；LSTM模型网络结构为1×5×1。

3.2 模型验证

根据所提出的预测模型，可建立3个单项预测模型，根据这3个单项预测模型，理论上可建立GM-ARIMA、GM-LSTM、ARIMA-LSTM共3个2维组合模型和GM-ARIMA-LSTM 1个3维组合模型。首先将一级融合后的安全状态系数作为输入，建立单项预测模型，模型建立好后对后期的安全状态系数进行预测。根据单项预测模型建立基于简单平均原理的简单平均组合模型和基于最小误差平方与最小二乘法的最优加权组合模型，然后利用模型比较的4个指标以及后期数据的相对误差对组合模型的预测精度进行检验，选出拟合效果最好的TBM拆装装置安全预警模型。

建立的3个单项预测模型的预测结果与真实值之间的拟合效果如图2所示。

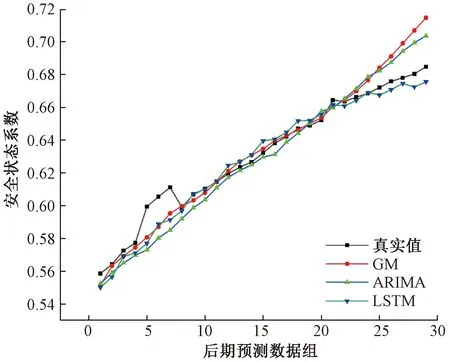
图2 单项预测模型拟合效果Fig.2 Fitting effect of single prediction model

单相预测模型GM、ARIMA和LSTM最大相对误差分别为4.37%、4.40%和3.74%，LSTM模型的相对误差最小，模型后期预测的结果比真实值稍小。GM和ARIMA模型的相对误差较大，虽然小于5%，但根据图2可以看出两者在后期所预测的结果比真实值高，真实值与预测值的偏差也比LSTM模型的偏差大得多。

根据简单平均原理，简单平均组合模型中GM-ARIMA、GM-LSTM和ARIMA-LSTM中各单项模型权重均为0.5；GM-ARIMA-LSTM中各单项模型权重均为0.33。简单平均组合模型与安全状态系数真实值拟合效果如图3所示。

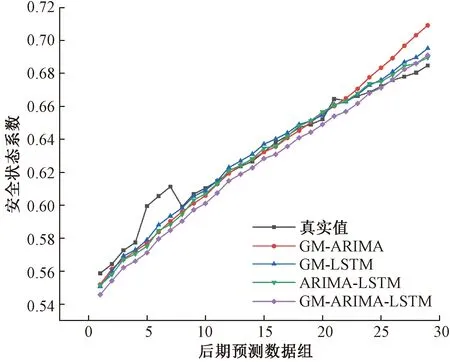
图3 简单平均组合模型拟合效果Fig.3 Fitting effect of Simple average combined model

简单平均组合模型GM-ARIMA、GM-LSTM、ARIMA-LSTM和GM-ARIMA-LSTM最大相对误差分别为3.76%、3.43%、4.07%和4.71%，从图3中可以明显看出，4个简单平均组合模型后期的预测值都比真实值大，后期拟合效果比较差。

通过最小误差平方和最小二乘法可解决最优加权组合模型权重分配问题，求得GM-ARIMA的权重为k1=0.64，k2=0.36；GM-LSTM的权重为k1=0.29，k2=0.71；ARIMA-LSTM的权重为k1=0.18，k2=0.82；GM-ARIMA-LSTM的权重为k1=0.21，k2=0.10，k3=0.69。最优加权组合模型与安全状态系数真实值拟合效果如图4所示。

图4 最优加权组合模型拟合效果Fig.4 Fitting effect of optimal weighted combination model

最优加权组合模型GM-ARIMA、GM-LSTM、ARIMA-LSTM和GM-ARIMA-LSTM最大相对误差分别为3.78%、3.55%、3.85%和3.67%，从图4可以看出，除GM-ARIMA后期预测的结果比真实值偏差较高外，其他3个组合预测模型都包含有LSTM模型，且后期预测的结果都接近真实值，其中GM-LSTM和GM-ARIMA-LSTM这两个组合预测模型更贴近真实值，拟合效果更好。

根据模型所预测的结果，单相预测模型和组合预测模型预测精度的4个指标比较如表4所示。

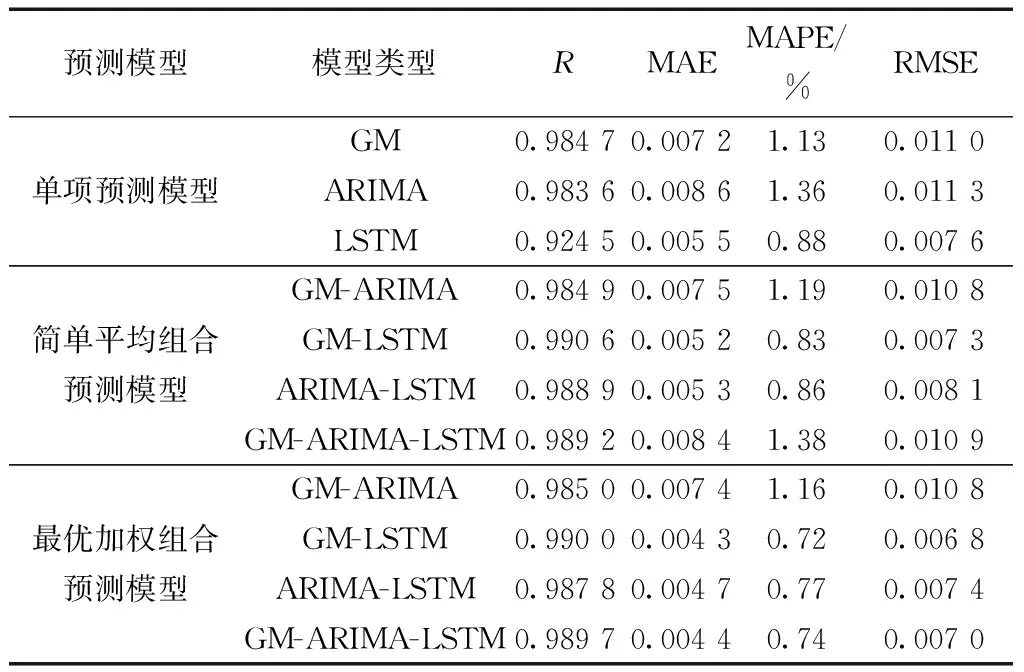
表4 模型预测精度对比Table 4 Model prediction accuracy comparison

由表4可知，单项预测模型中GM模型的R最高，LSTM模型的MAE、MAPE、RMSE最小，结合图2说明单项预测模型中LSTM模型拟合效果较好。简单平均组合预测模型中GM-LSTM模型的4个指标均要好于其他3个模型，且R是所有模型的最大值(0.990 6)，在简单平均组合模型中此模型的拟合效果最好。最优加权组合预测模型的4个指标数据大部分都要优于前两类模型，而且最优加权组合预测模型中GM-LSTM模型的MAE、MAPE、RMSE的值比所有模型都要小，因此比单项预测模型和简单平均组合模型稳定性更强，后期预测结果精度更高，效果更好。虽然GM-LSTM模型指标数据都比GM-ARIMA-LSTM模型要好，二者的预测值都比真实值大一些，都能及时反映TBM拆装装置吊装TBM主机时的安全状态。但由于二者的4个指标数据非常接近，且在图4序号为20～30的后期预测数据组中，GM-ARIMA-LSTM模型的预测值与真实值之间的相对误差比GM-LSTM模型的相对较小，其预测值更贴近真实值，后期拟合效果最好，同所有预测模型中后期预测精度相比也较好。因此根据以上分析，选择最优加权组合预测模型中权重为(0.21，0.10，0.69)的GM-ARIMA-LSTM模型作为二级融合的安全预警模型。

4 结论

(1)根据拆装装置吊装TBM主机时所采集的2组钢丝绳拉力数据、4组液压缸压力数据、1组偏载角数据、1组装置起升高度数据为基础，通过与对应层次分析法-熵权法融合算法所得权重融合得出安全状态系数，从而完成安全预警模型的一级融合，安全状态系数可以对比作业警度与风险等级，得到此时拆装装置的安全状态。

(2)组合预测模型利用单项预测模型的有效信息，有效弥补了单项预测模型的缺陷，通过R、MAE、MAPE、RMSE 4个指标的检验可以确定组合预测模型是优于单项预测模型，适合对TBM拆装装置安全作业状态系数进行有效的预测分析。

(3)最优加权组合预测模型的拟合效果要明显优于简单平均组合模型，而且最优加权组合预测模型中GM-LSTM与GM-ARIMA-LSTM精度都非常高，但后者的后期拟合效果更好，因此选用最优加权组合预测模型中权重为(0.21，0.10，0.69)的GM-ARIMA-LSTM模型作为二级融合的安全预警模型，并与一级融合结合，构建基于两级信息融合的TBM拆装装置作业安全预警模型。