洞桩法导洞开挖方案分析与优化
2023-02-11李家正杨浩杰冯吉利
李家正, 杨浩杰, 冯吉利*
(1.中国矿业大学(北京)深部岩土力学与地下工程国家重点实验室, 北京 100083; 2.中国矿业大学(北京)力学与建筑工程学院, 北京 100083)
随着中国城镇化水平的不断提高,许多城市都出现了地面交通拥堵问题,因此如何安全、高效地利用城市地下空间资源成为缓解交通压力的重要方式。地铁作为城市地下运营的一种公共交通方式,可以有效地缓解地面交通拥堵问题。而地铁常常修建在繁华的城市地段,施工时必然会引发地表变形,所以在施工过程中应尽量减小地表变形,确保不会对交通产生影响,避免危及地铁周边建筑物的安全。因此,优化施工方案,尽量使地铁施工引发的地表变形最小,是地铁设计和施工中非常重要的技术工作。
目前,众多学者对地铁建设过程中导洞开挖引发的地表变形规律进行了相关理论研究和工程模拟分析。陈春来等[1]在Peck公式基础上,推导出双线水平平行盾构隧道施工引发的三维土体沉降预测公式。邵珠山等[2]根据随机介质法推导出不同隧道形式下的非均匀收敛预测模型。周稳弟等[3]采用数值仿真与现场实测相结合的方法,对洞桩法施工过程中的地表沉降及边桩受力进行分析,得出导洞开挖和扣拱施工对地层的扰动较大,地表沉降最大值发生在车站中轴线上方,符合 Peck公式。刘运思等[4]以十里河车站为工程背景,研究不同覆跨比、不同导洞开挖顺序、不同土层参数对地表变形的影响。宋高锐等[5]通过数值分析手段,对暗挖隧道不同施工工法进行模拟,得到最优工法为交叉中隔壁(cross diaphragm,CRD)法。彭云涌等[6]采用数值分析分析浅埋小净距隧道开挖引发的地表沉降和支护变形规律,得出先行隧道及后行隧道的错开步距最佳为 40 m。李金奎等[7]依托实际工程,通过正交设计根据开挖方式、开挖顺序、开挖步距、作业方式4个影响因素对开挖方案进行优化,得出最优开挖方案为:采用台阶开挖,选择先两边、中间、后下层的开挖顺序,选用 1 m 的开挖步距,选用流水作业方式。曹德更等[8]依托实际工程背景,研究洞桩(pile-beam-arch,PBA)工法中导洞开挖面距对地表沉降量的影响,得出开挖面距为15 m时较为合适。
已有文献对地表变形规律的研究较多[1-6],但对于确定开挖方式后如何选择具体开挖方案的研究较少[7-8]。确定开挖方案需要考虑开挖顺序与开挖错距两个因素,若同时考虑开挖顺序和开挖错距,需要进行大量实验得到最优解,通常将开挖错距设定为同一个值来简化优化过程。但这种简化方式无法体现开挖错距对地表变形的影响,因此,现参考实际工程的开挖错距确定最佳开挖顺序,进而得到开挖错距与地表变形的函数关系。以北京17号线东大桥地铁车站为工程背景,通过Midas对群洞开挖进行模拟。采用地表沉降量和沉降槽宽度表征地表变形,依据Peck公式拟合地表变形曲线,通过正交实验设计对开挖顺序进行分析,得到最优开挖顺序,在此基础上通过回归方法,确定开挖错距对地表变形的函数关系,确定最佳方案。
1 工程背景
1.1 工程概况
17号线东大桥车站全长336.8 m,南侧标准段为双层、双柱三跨结构,宽度28.9 m,中心里程处单层结构的覆土厚度约15.18 m,设上下两层共计8个导洞。
1.2 工程地质概况
如表1所示,车站施工范围内土体自上而下分为8层,依次为素填土、粉质黏土、圆砾、粉质黏土、圆砾、中砂、卵石、细粉砂。注浆材料采用水泥-水玻璃,对拱顶外0.5 m范围内土体进行预注浆加固。初期支护采用C20网喷混凝土加钢格栅,厚度为0.3 m。

表1 材料物理力学参数Table 1 Physical and mechanical parameters of materials
1.3 开挖工序
导洞开挖顺序为先上后下,先边后中,同层近邻导洞错距开挖。导洞开挖顺序依次为①→④→②→③→⑤→⑧→⑥→⑦。参考实际工程,开挖错距设置为20 m。开挖方式为上下台阶法开挖,此处简化为整体开挖,循环开挖距离2 m。开挖前对土体进行预注浆加固,加固范围超前开挖面2 m,开挖后及时施作初期支护。结构横断面及导洞编号如图1所示。
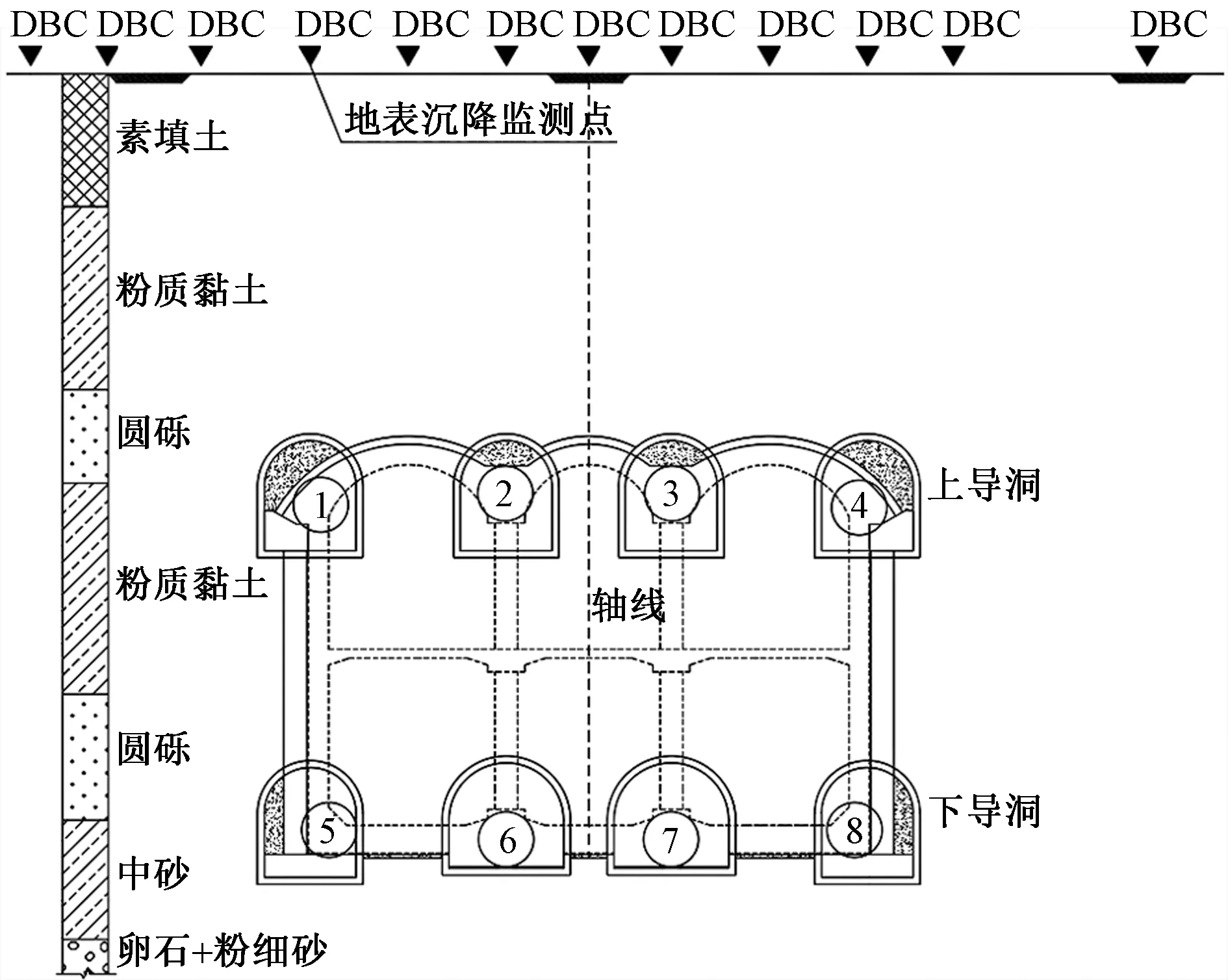
图1 结构横断面及导洞编号Fig.1 Structure cross section and pilot tunnel number
1.4 监测方案
如图2所示,选取车站南侧标准段A-A断面监测数据进行分析。当南段导洞施工完毕后,将A-A断面监测数据作为地表变形。
2 数值模型与验证
2.1 模型建立
计算采用Midas模拟开挖,模型边界距边导洞中心线距离为结构尺寸的3~5倍时,土体受施工开挖影响不明显。考虑导洞间开挖顺序及导洞间的错距要求,开挖长度拟定为36 m。因此,建立X×Y×Z=150 m×36 m×70 m三维模型。模型上表面施加20 kPa地面超载,下表面设置为固定端约束,对四周土体施加法向约束。假定土层均匀,服从修正摩尔-库伦准则,初期支护服从弹性准则,采用实体单元模拟。采用钝化实现导洞土体的开挖,荷载释放系数分别设定为0.5、0.25和0.25[9]。由于浅埋暗挖法不允许带水作业前期已进行地层降水[10]。数值分析不考虑地下水的影响,模拟开挖模型如图3所示。

图3 数值分析模型Fig.3 Numerical analysis model
2.2 模型验证
如图4所示,群洞开挖完毕后,横向地表变形规律为沉降量随着距车站轴线距离的增大而减小,轴线附近的沉降量变化率最大,沉降关于轴线对称,形成一个“凹槽”的变形规律。

图4 位移云图Fig.4 Displacement nephogram
如图5所示,依据东大桥车站A-A断面导洞施工方案进行数值分析,将模型运算结果与现场实测[8]进行对比,可知,模拟得到的地表变形规律与实测规律基本吻合,地表沉降曲线近似标准正态分布。但与现场实测结果仍有差距,例如数值分析所得地表最大沉降量为41.906 3 mm,实测为40.153 8 mm,偏差4.36%,主要是由于以下几个原因造成。

图5 地表沉降量实测与数值分析对比Fig.5 Comparison of measured and numerical analysis of ground subsidence
(1)将土层概化为各向同性且水平均匀分布的,而实际上土层是各向异性且非水平均匀分布的。
(2)计算模型的应力释放系数与实际情况下的真实值存在一定偏差。
(3)实际工程中无法做到完全排水施工,而在模型未考虑这种情况。
采用数值模型进行计算,结果表明模型预测值与现场实测地表变形规律基本一致,验证了模型的合理性。
3 地表变形公式
目前地下隧洞开挖引起的地表变形主要采用Peck公式和随机介质理论进行计算。其中随机介质理论是将开挖土体视为“随机介质”,将隧道开挖引发的地表沉降看作土体开挖造成的影响叠加之和,根据隧道断面形式确定积分域,代入推导的收敛模型,进而得到地表变形的预测曲线[2]。Peck公式根据工程经验,通过高斯公式得到单隧洞开挖地表沉降的预测曲线。随后的研究工作基于随机介质理论、Peck公式推导出多隧洞沉降预测公式[1-2]。
以东大桥工程背景为依托,将8导洞组成的群洞视为整体,根据Peck公式,认为群洞施工完成后地表变形曲线关于轴线对称,利用高斯公式分析不同开挖顺序,不同开挖错距下的地表变形规律,并进行方案优化。
地表变形的数学表达式为
S(x)=-Smaxexp[-x2/(2i2)]
(1)
式(1)中:i为沉降槽宽度,即地表变形曲线中心到曲线拐点的距离;Smax为地表最大沉降量。
当远离车站轴线一定范围时,地表沉降量迅速减少,此处地表变形曲线的弯曲程度达到最大,曲率K取到最大值,即
(2)
式(2)中:S′为地表变形一阶导数;S″为地表变形二阶导数。
为求得地表变形曲线曲率取到最大值的点,利用MATLAB对式(2)进行非线性优化。参考模拟车站,最大沉降值Smax取为40 mm,i的取值范围为10~15 m。如图6所示,得到最大曲率点横坐标与沉降槽宽度i的关系,|x|=1.732 05i。
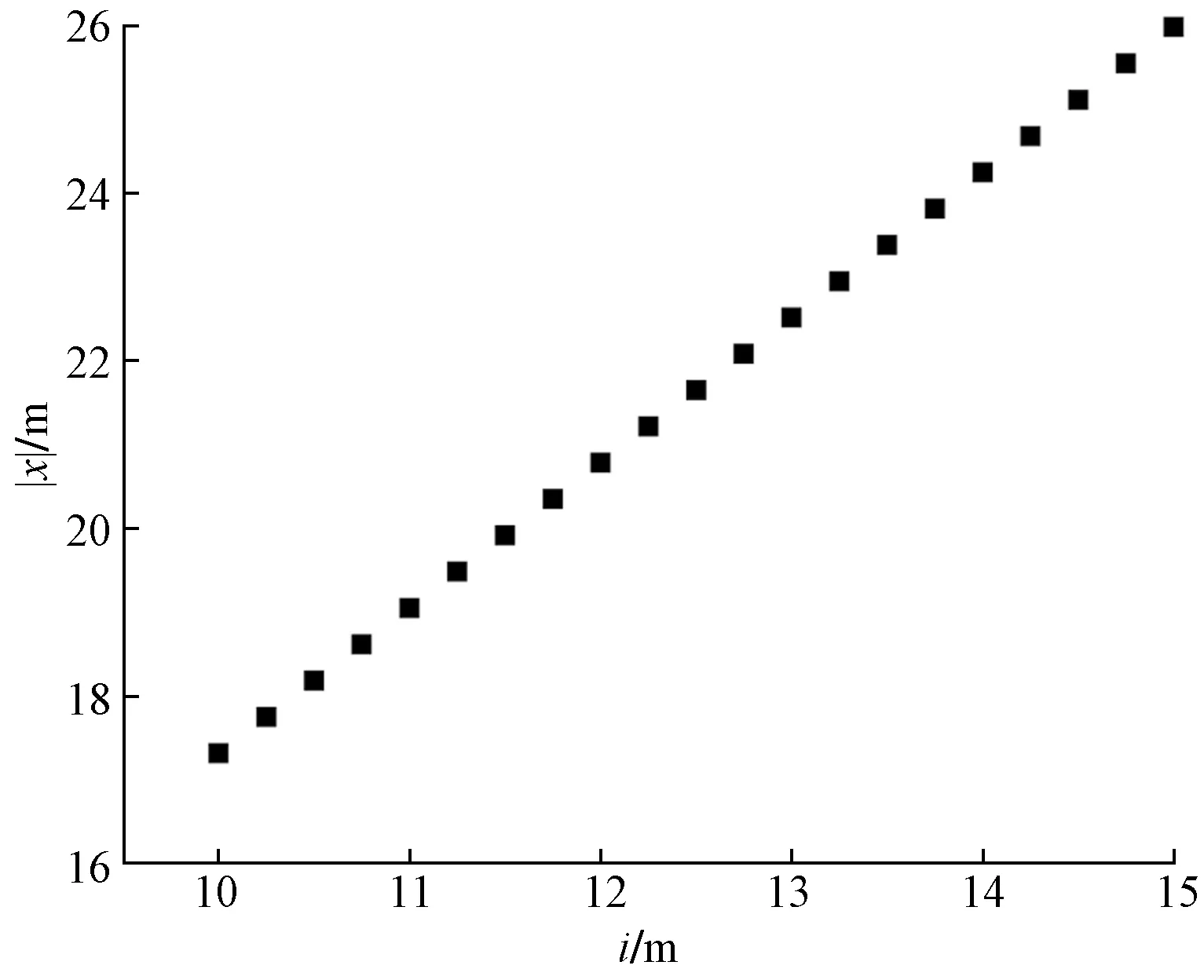
图6 拟合曲线Fig.6 Fitting curve
对现场实测结果进行拟合表明,i=12.98 m时,相关系数为0.93,认为拟合结果与现场实测结果高度相关。通过拟合结果,地表沉降范围为71 m,约为车站结构跨度的2.5倍。地表监测线上横坐标绝对值大于22 m时,沉降量迅速减小,与相关文献结论基本一致[3]。
4 施工方案优化
群洞采用对称开挖可以减小支护结构的不均匀受力情况,所以针对对称开挖顺序进行优化。开挖错距设定为同一值时,可能不是最优解,因此将开挖错距细化,研究开挖错距与地表变形的函数关系。开挖顺序、开挖错距的确定方法如下。
(1)开挖顺序需要确定以下3个因素:先开挖上层还是先开挖下层(层间开挖顺序);上层群洞的开挖顺序;下层群洞的开挖顺序。以上3个因素确定后就可以确定群洞整体的开挖顺序。
(2)开挖错距需要确定以下3个因素:上层导洞错距开挖的错距,下层导洞错距开挖的错距,以及上下层导洞错距开挖的错距(单层后开挖导洞在开挖一定距离后进行下一层导洞开挖)。以上3个因素确定后就可以确定群洞整体的的开挖错距。
4.1 导洞开挖顺序分析
以8导洞模拟开挖为原型,采用正交试验设计[11],研究开挖顺序对地表变形的显著程度,同时对开挖顺序进行优化。
正交设计依据正交性原理,其核心思想为在实验范围内挑选具有代表性的点进行实验设计,确保相对准确的同时大规模减少实验次数。参照标准正交表将导洞施工顺序描述为层间开挖顺序、上层开挖顺序和下层开挖顺序3个因素,研究3个因素对地表变形的影响,每个因素各有两个水平,如表2所示。依据正交实验原理,采用L4(23)正交表,给出4种组合方案,如表3所示。

表2 实验因素和水平Table 2 Experimental factors and levels

表3 正交设计实验方案表Table 3 Scheme of the orthogonal design test
为了简化正交表将各因素水平进行简化,约定如下。
对于层间开挖顺序(A):先上后下记为1,先下后上记为2。
对于上层开挖顺序(B):先边后中记为1,先中后边记为2。
对于下层开挖顺序(C):先边后中记为1,先中后边记为2。
如图7所示,对于每一组实验,仅将开挖顺序作为自变量,其他部分保持不变。计算开挖完毕后地表最大沉降量及沉降槽宽度两个结果。
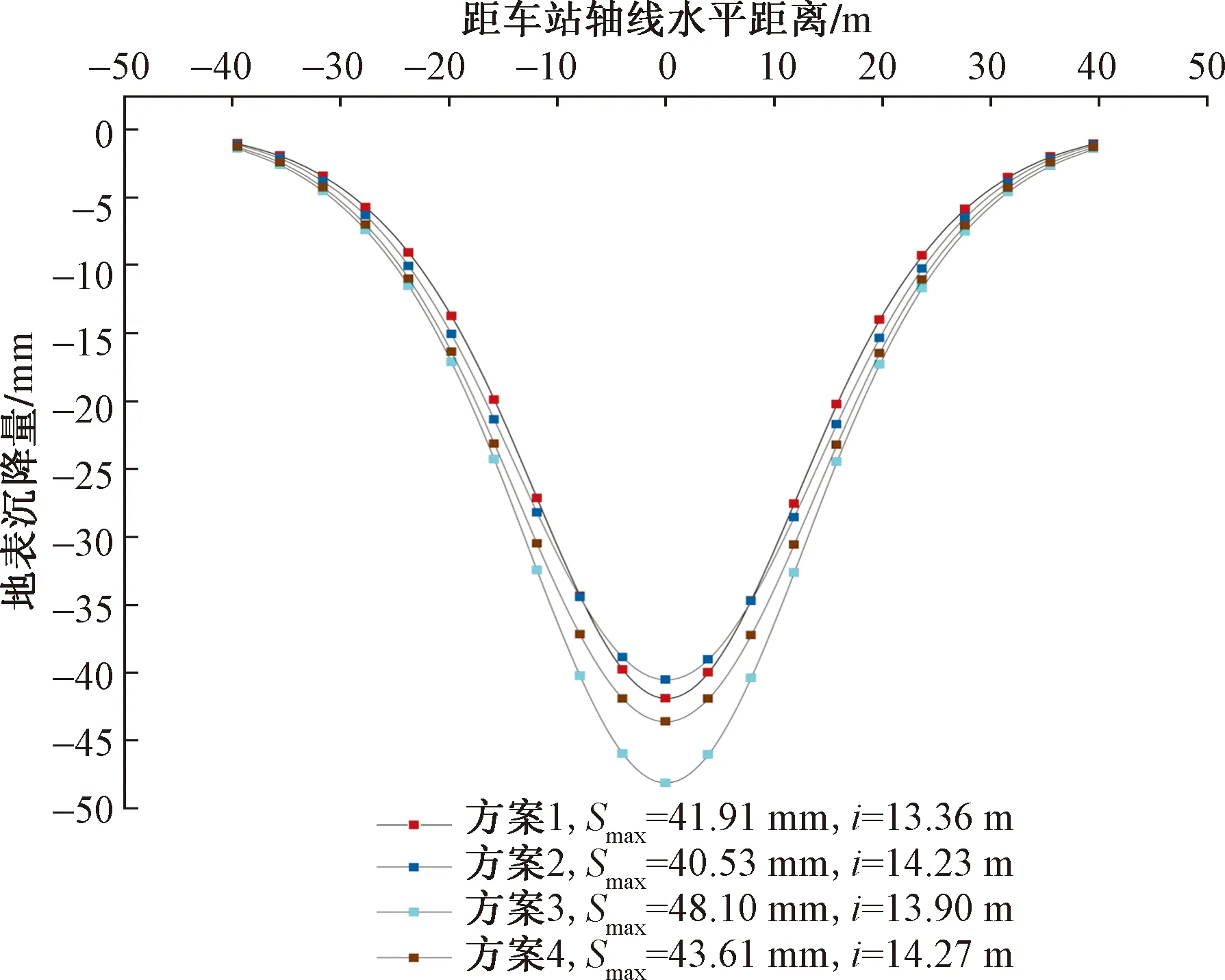
图7 正交设计实验结果Fig.7 The results of orthogonal design test
如表4所示,将根据正交设计,采用极差分析法,对各因素的主次关系进行研究。具体步骤如下。
(1)计算因素结果之和Ki值,表示因素采用第i参数水平时对应的方案结果之和。
(2)计算因素结果之和的均值ki=Ki/n,其中n为因素对应的水平个数,取n=2。

表4 正交实验结果分析Table 4 Analysis of orthogonal experiment results
(3)计算极差R,对于任一因素有R=max{ki}-min{ki},极差越大,对应因素对结果影响越显著。
根据分析结果对各因素的极差进行排列。对于地表最大沉降量:A层间开挖顺序>B上层开挖顺序>C下层开挖顺序;对于沉降槽宽度:B上层开挖顺序>A层间开挖顺序>C下层开挖顺序。
如图8所示,从减小地表最大沉降量角度出发,最佳的开挖顺序是A1B2C1,从减小沉降槽宽度角度出发,最佳的开挖顺序是A1B1C1。
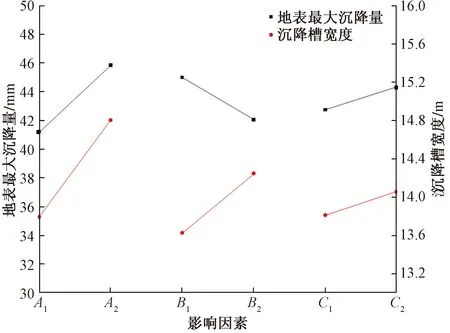
图8 因素水平关系Fig.8 Factor level relationship
4.2 导洞开挖错距分析
4.2.1 均匀实验设计
通过对开挖顺序进行研究,采用方案1时,群洞开挖引发的沉降槽宽度最小,采用方案3时,群洞开挖引发的地表最大沉降量最小。以开挖错距为自变量对沉降槽宽度进行优化,开挖顺序采用方案1研究开挖错距与地表变形的关系。
为确保实验准确性,每个因素需要取较多水平,采用正交设计,需要进行大量实验。因此,本次研究采用均匀设计。均匀设计从均匀性角度出发,不考虑“整齐可比”性,核心思想为将实验点均匀散布在实验范围内,在极大减少实验次数的条件下,确保实验范围内结论的相对准确。
参考均匀设计[12],从均匀表U9*(94)中,取出第2、3、4列进行均匀设计,均匀设计偏差D=0.198 0。将导洞开挖错距描述为层间开挖错距、上层开挖错距和下层开挖错距3个因素,通过函数关系计算出地表变形。参考实际工程,最小开挖错距取为4 m,最大开挖错距取为20 m,每个因素各取9水平,如表5所示。给出9种组合方案,如表6所示。
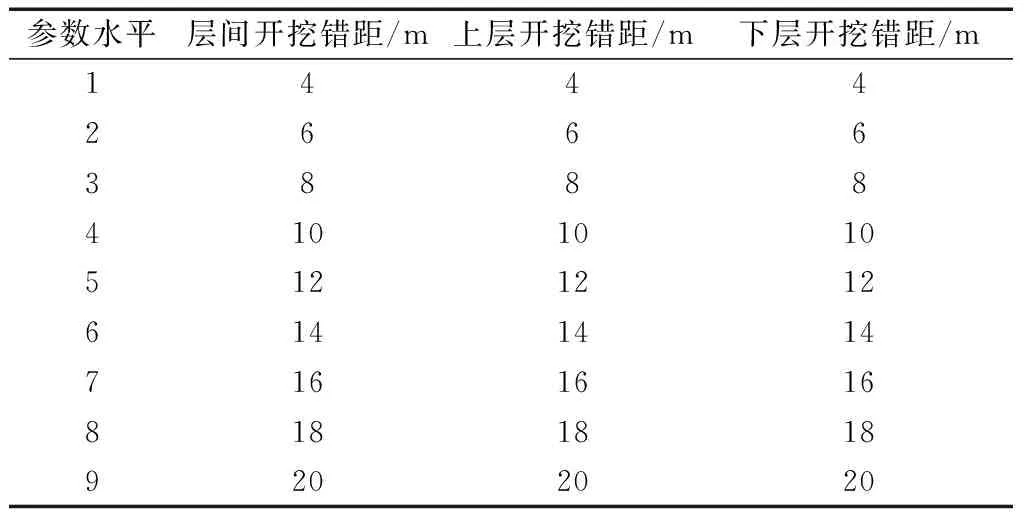
表5 实验因素和水平
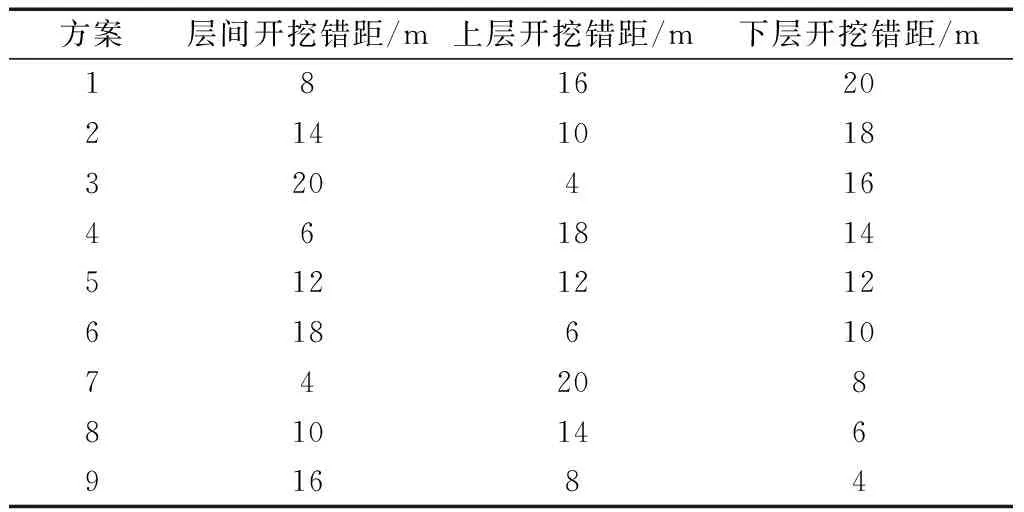
表6 均匀设计实验方案表Table 6 Uniform design experimental scheme table
如图9所示,对于每一组实验,仅将开挖错距作为自变量,其他部分保持不变。计算开挖完成后地表最大沉降量及沉降槽宽度两个结果。

图9 均匀设计实验结果Fig.9 The results of uniform experimental test
4.2.2 地表变形回归分析
以地表最大沉降量为目标函数,对结果进行二次多项式逐步回归分析,得
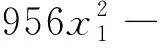
(3)
式(3)中:y1为地表最大沉降量;x1为层间开挖错距;x2为上层开挖错距;x3为下层开挖错距。
F检验临界值F0.05(4,4)=6.39<9.246 3,回归方程显著,复相关系数R=0.95,剩余标准差SSE=0.37,调整后相关系数Radj=0.90,由此可见地表最终沉降量与回归方程中各因素密切相关。
以沉降槽宽度为目标函数,同理得
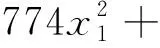
(4)
式(4)中:y2为沉降槽宽度;x1为层间开挖错距;x2为上层开挖错距;x3为下层开挖错距。
F检验临界值F0.05(4,4)=6.39<50.227 3,回归方程显著,复相关系数R=0.99,剩余标准差SSE=0.02,调整后相关系数Radj=0.98,由此可见沉降槽宽度与回归方程中各因素密切相关。
4.2.3 显著性分析
4.2.4 回归方程验证
如表7所示,将计算值与实测值进行对比,x1、x2、x3均取为20 m。实测地表最大沉降量为40.15 mm,函数计算值偏差4.9%,偏差较小。实测沉降槽宽度为12.98 m,函数计算值偏差4.2%,偏差较小。因此,进一步验证了本次研究中实验安排良好,同时说明通过回归分析得到的回归方程及利用非线性优化处理结果是可靠的。

表7 优化结果及预测值对比Table 7 Comparison of optimization results and predicted values
4.2.5 最佳参数确定
以沉降槽宽度作为优化对象,根据非线性规划原理对y1进行单目标优化。
约束条件为
(5)
通过MATLAB中的MultiStart方法对单目标y1进行全局优化,起始点设置为1 000个,优化结果如表8所示;当层间、上层、下层开挖错距为4、20、20 m时,沉降槽宽度取得最小值,此时地表最大沉降量和沉降槽宽度分别是42.18 mm和13.33 m。

表8 优化结果Table 8 Optimization results
5 结论
以17号线东大桥地铁车站为工程背景,对群洞开挖进行模拟。参考Peck公式采用地表沉降量和沉降槽宽度表征地表变形,采用Midas结合正交设计和回归分析研究采用对称开挖施工时,开挖顺序和开挖错距与地表变形的函数关系,最终得到最优开挖方案。得出以下结论。
(1)实测地表最大沉降量为40.15 mm,数值分析得到的地表最大沉降量为41.91 mm,模拟值与实测值相差4.4%,实测地表沉降曲线沉降槽宽度为12.98 m,数值分析求得13.36 m,模拟值与实测值相差2.9%。因此,认为数值分析比较准确。
(2)采用正交设计确定开挖顺序对地表变形影响的主次关系。根据因素间的水平关系得到采用对称开挖的情况下,先开挖上层后开挖下层,先开挖边导洞后开挖中导洞时,沉降槽宽度最小;先开挖上层后开挖下层,上层采用先中后边,下层采用先边后中的开挖顺序时,地表最大沉降量最小。
(3)采用回归方法得到采用先上后下、先边后中的开挖顺序时,开挖错距与地表变形的函数关系,了解到层间开挖错距的平方项对地表变形的影响最显著,同时从减小沉降槽宽度角度出发,得到最优开挖方案为先上后下,先边后中,层间、上层、下层开挖错距依次为4、20、20 m。
