隧道开挖超小变形监测与数值仿真分析
2023-02-11杨三强曹亚文张丹
杨三强, 曹亚文, 张丹
(河北大学建筑工程学院河北省土木工程监测与评估技术创新中心, 保定 071002)
隧道在开挖过程中,会破坏周围土体的平衡状态,引发地表沉降槽,导致地表发生沉降,使得地表以及地表建筑发生变形,对人民的生命财产造成威胁。因此在隧道施工过程中,预测和控制地表沉降显得尤为重要。隧道施工引起的地表沉降问题的研究方法大致可以总结为3类,即经验公式[1]、模型试验法[2]和智能算法[3]。自1969年Peck提出peck公式之后,很多学者都在此基础上对Peck公式进行改进[4-6],而由于Peck公式在应用时有较大的局限性,因此随机介质理论成为研究地层位移及变形的最为广泛的实用的方法之一[7-9]。
近年来,许多国内外学者对隧道开挖引起的地表沉降进行了深入研究。Cai等[10]基于随机介质理论,建立了隧道冻结施工时地表三维隆起位移的解析解,并应用到实际工程中。Singh等[11]通过建立有限元模型研究了土壤条件和隧道参数对地铁隧道地表沉降的影响,并利用回归分析的方法证明了土壤条件和隧道参数对地表沉降有显著影响。王辉等[12]基于随机介质理论极坐标表达式,得到了不同断面、不同尺寸的并行隧道开挖地表沉降量及其分布规律。王海龙等[13]通过Midas-GTS建立仿真模型,并与实测数据进行对比分析,研究了岩柱在不同加固形态及不同加固高度下隧道地表沉降的变化规律。李加辉等[14]利用Midas/GTS有限元软件通过设定多个模拟工况建立了三位有限元模型,利用Origin对模拟结果进行拟合,研究了曲线隧道施工引起地表沉降槽峰值偏移规律。
综上所述,大多数学者都通过仿真模拟研究了隧道地表沉降的变化规律,而对于隧道的超小变形规律和预测的研究还尚少,因此在前人研究的基础上,现基于随机介质理论的简化公式,利用MATLAB编写程序对秦皇岛角山隧道地表的实测数据进行拟合,反分析求得在超小变形中随机介质理论中的两个参数隧道收敛面积ΔA和地层影响角β,并研究ΔA与tanβ以及ΔA与隧道埋深Z的关系。同时,通过滚动预测的方法建立反向传播(back propagation,BP)神经网络模型,对角山隧道地表未来的超小变形值进行预测。
1 随机介质理论原理及简化
随机介质理论认为,地表的沉降可以看成是由无数个微小单元在隧道断面收敛区域内塌陷效果的叠加[15]。对于地层采用整体坐标系(x,o,z),对于隧道开挖部分采用整体坐标系(ζ,o,η),假设隧道开挖断面大小为Ω,隧道开挖半径为R,埋深为Z,每个单元dζdη开挖后完全塌落,则整个断面完全塌落时地表的沉降值为
(1)
式(1)中:β为地层影响角;η为单元体中心距地表的垂直距离;ζ为单元体中心距隧道中线的水平距离;X为地表点距单元体中心的水平距离。
式(1)是分析当隧道完全塌落时所引起的地表沉降,但实际隧道开挖不可能完全塌落。隧道建成后断面由Ω变为ω,半径由R变为r(如图1所示),其中ΔA=Ω-ω=π(R2-r2),H为隧道中心埋深。则此时的地表沉降值[16]为
S(X)=SΩ(X)-Sω(X)
(2)
隧道开挖之后,断面会发生收敛,这种收敛分为均匀收敛和不均匀收敛,示意图如图2和图3所示。在均匀收敛情况下,一般认为断面向中心收敛了ΔR,这种情况比较理想化。而不均匀收敛时,认为隧道断面顶部向下收敛了2ΔR,断面底部则不发生收敛,这是由于在实际隧道开挖过程中会受到施工方法、岩石性质和地层条件等影响,随机介质理论一般情况下适用于断面的均匀收敛。两种收敛模式积分界限对比如表1所示。

图1 隧道开挖前后断面收缩图Fig.1 Shrinkage of tunnel section before and after excavation
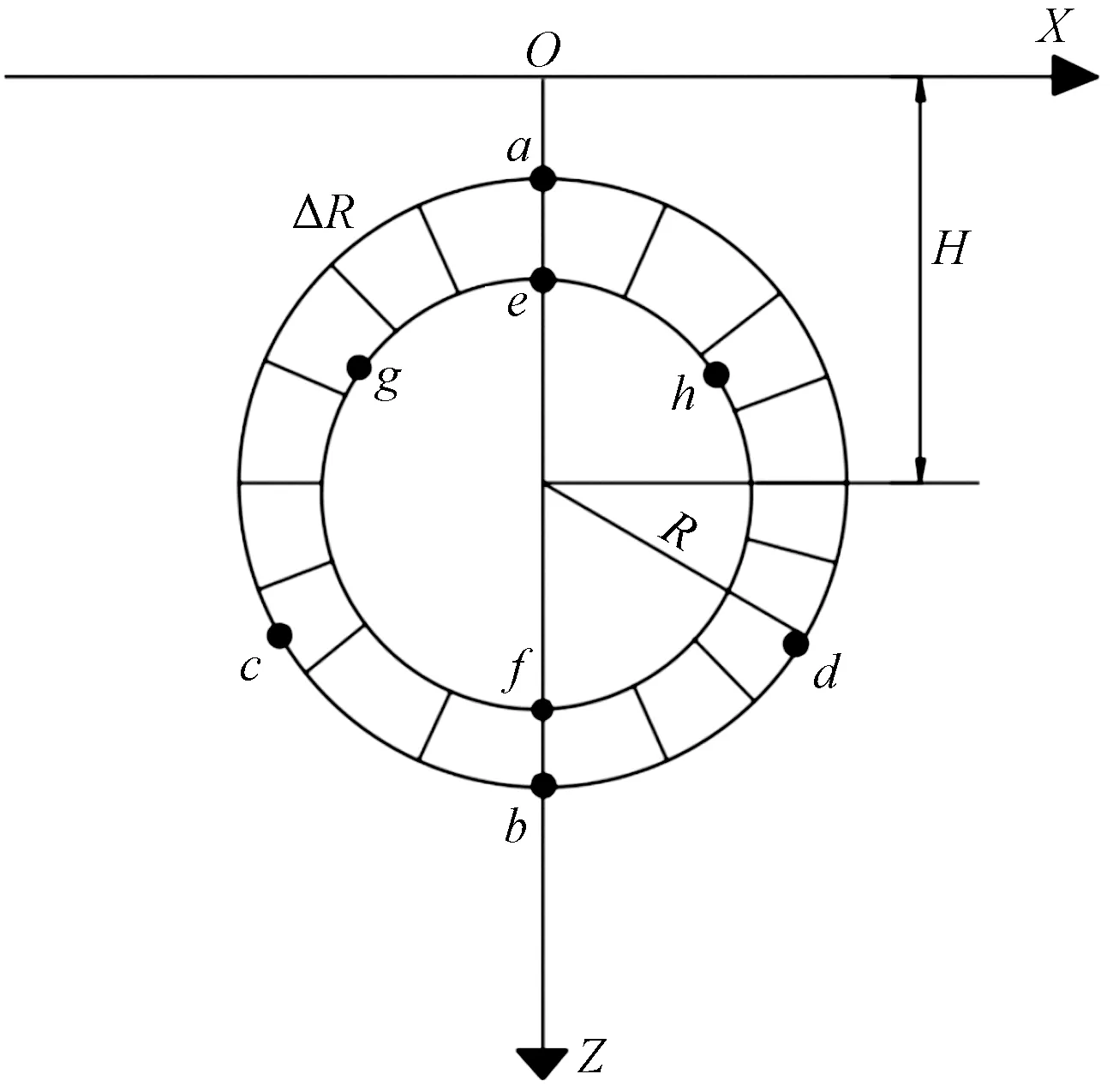
图2 隧道断面均匀收敛示意图Fig.2 Uniform convergence of tunnel section
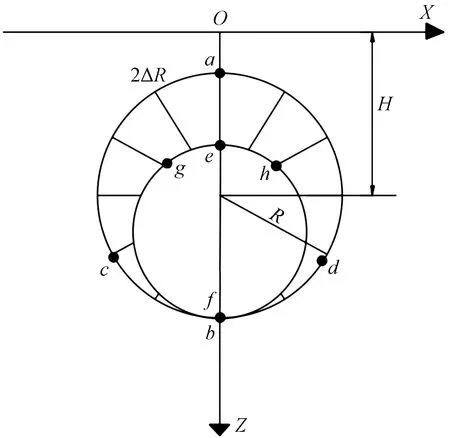
图3 隧道断面不均匀收敛示意图Fig.3 Uneven convergence of tunnel section
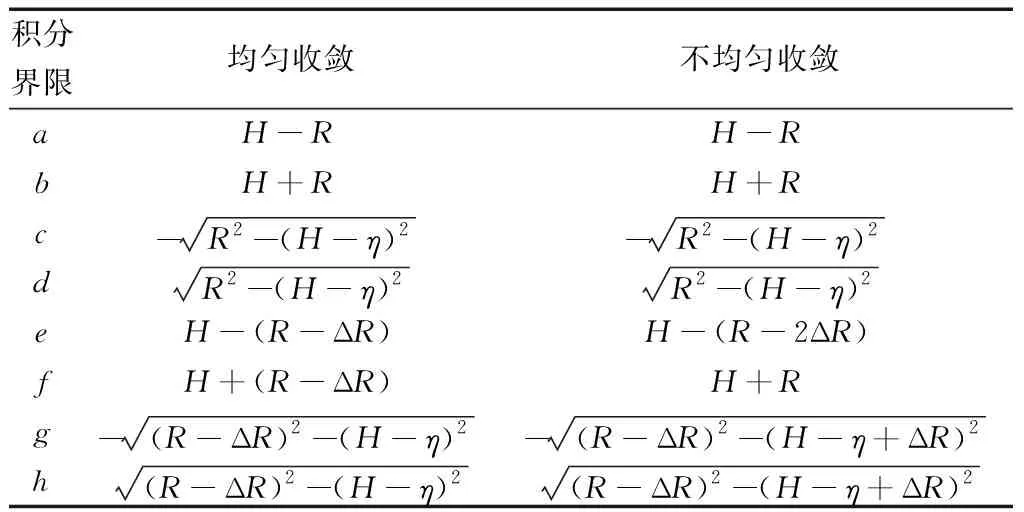
表1 两种收敛模式积分界限对比Table 1 Comparison of integral bounds between the two convergence modes
韩煊[17]通过编写程序研究了这两种收敛方式引起地表沉降计算结果的差异,研究结果表明,采用不均匀收敛方式比采用均匀收敛的方式引起的地表沉降槽窄而深,这个结论与学者刘波等[18]得到的结论相同。同时文献[17]研究了隧道开挖后均匀收敛和不均匀收敛的隧道埋深下地表中心点沉降差异,结果表明二者随着隧道埋深的增加沉降差异减小,最大误差不超过20%。因此,按照Yang等[19]的随机介质理论简化公式对角山隧道的地表沉降实测数据进行拟合。公式为
(3)
式(3)中:ΔA为隧道开挖后的收敛面积;Z为隧道埋深。
2 工程概况及监测方案设计
2.1 工程概况
角山隧道位于秦皇岛市山海关区角山境内,下穿长城,属于国道G102改建工程。隧道起始于K47+380,属于浅埋暗挖隧道。隧道围岩主要为强风化-中风化混合花岗岩,较弱岩,局部为较软岩与较硬岩互层,岩体破碎,节理裂隙发育,碎裂状及块状结构,为了降低隧道掘进难度,隧道采用CO2预裂与机械法相结合的施工方法进行开挖。
2.2 监测方案设计
在距长城西侧100 m处布设5个断面,每个断面间隔10 m,分别为DM-1、DM-2、DM-3、DM-4和DM-5。隧道横断面监测点布置图如图4所示,其中隧道中线过D-6点。每个断面有11个监测点,每个监测点间隔5 m,距隧道中心线分别为-25、-20、-15、-10、-5、0、5、10、15、20、25 m。监测断面布置图如图5所示。
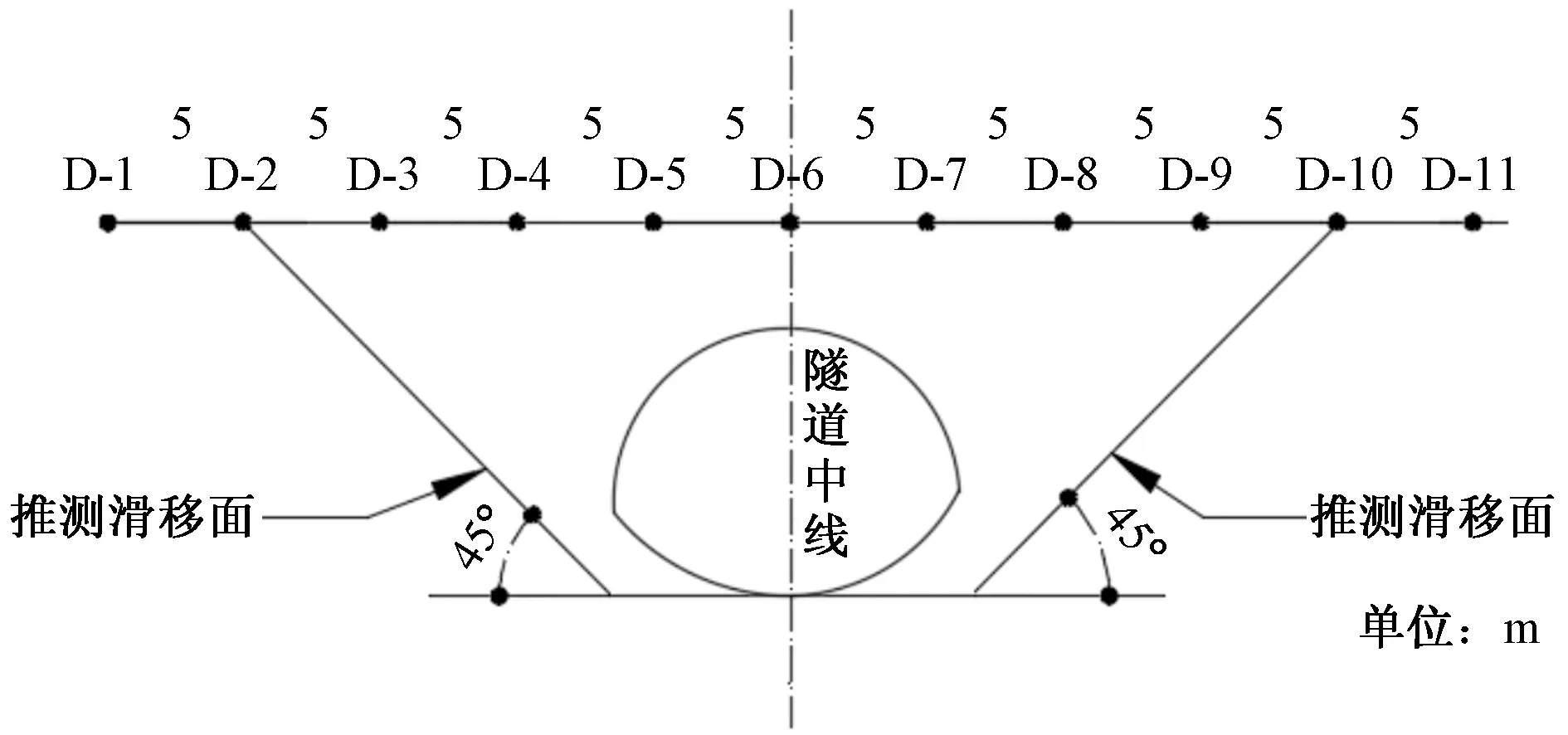
图4 横断面监测点布置图Fig.4 Cross-sectional distribution of monitoring points
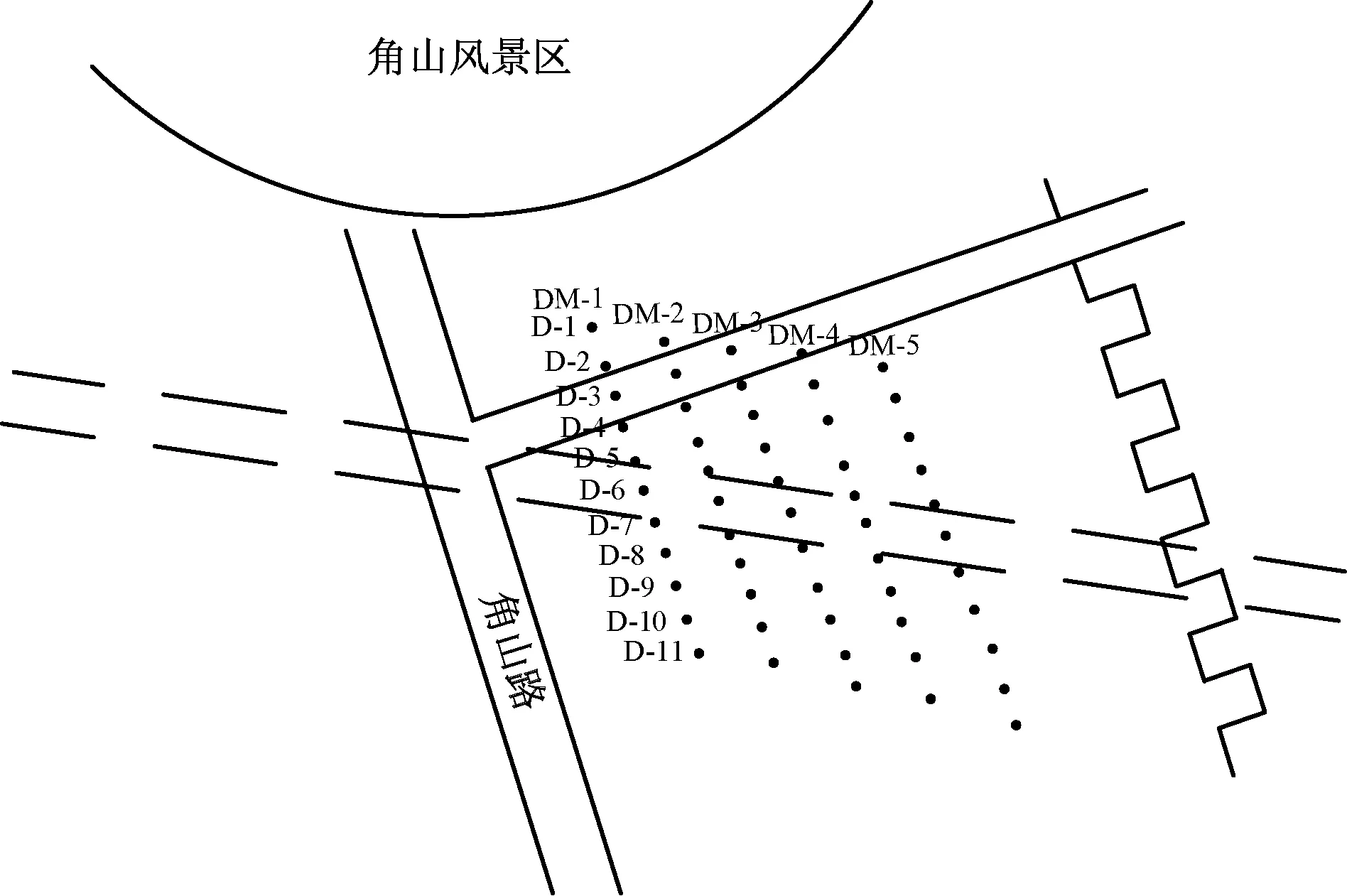
图5 监测断面布置图Fig.5 Monitoring section layout
对5个断面进行分析研究,利用MATLAB编写反分析程序,通过lsqcurvefit函数对实测的地表沉降数据进行拟合,并反演随机介质理论中的两个参数ΔA和β,各断面埋深及反分析结果见表2,各断面拟合图如图6~图10所示。

表2 各断面埋深及反分析结果Table 2 Burial depth and reverse analysis results of each section
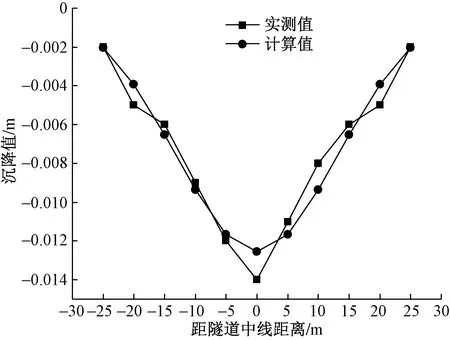
图6 DM-1地表沉降拟合Fig.6 DM-1 surface subsidence fitting

图7 DM-2地表沉降拟合Fig.7 DM-2 surface subsidence fitting

图8 DM-3地表沉降拟合Fig.8 DM-3 surface subsidence fitting

图9 DM-4地表沉降拟合Fig.9 DM-4 surface subsidence fitting
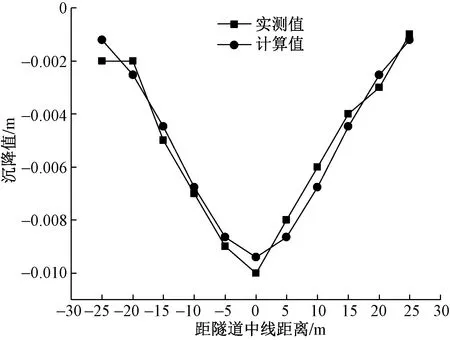
图10 DM-5地表沉降拟合Fig.10 DM-5 surface subsidence fitting
如图6~图10所示,随机介质理论计算结果与实测的地表沉降拟合结果较理想,最大沉降位置及曲线的变化趋势与实测数据基本保持一致。根据表2反分析结果可知,角山隧道断面收敛面积ΔA的平均值为0.338 8 m2,地层主要影响角β的平均值为21.680 3°。
3 计算参数与隧道埋深之间的关系
将表2反分析结果整理,得到ΔA与隧道埋深Z之间的关系,以及ΔA与tanβ之间的关系,如图11和图12所示。
如图11所示,ΔA比较离散,且随着隧道埋深Z的增加,ΔA逐渐减小,地层损失也逐渐减小,地表沉降随之减小。当Z为20.53 m时,隧道收敛面积ΔA接近0。

图11 ΔA与隧道埋深的关系图Fig.11 Relationship between ΔA and tunnel buried depth
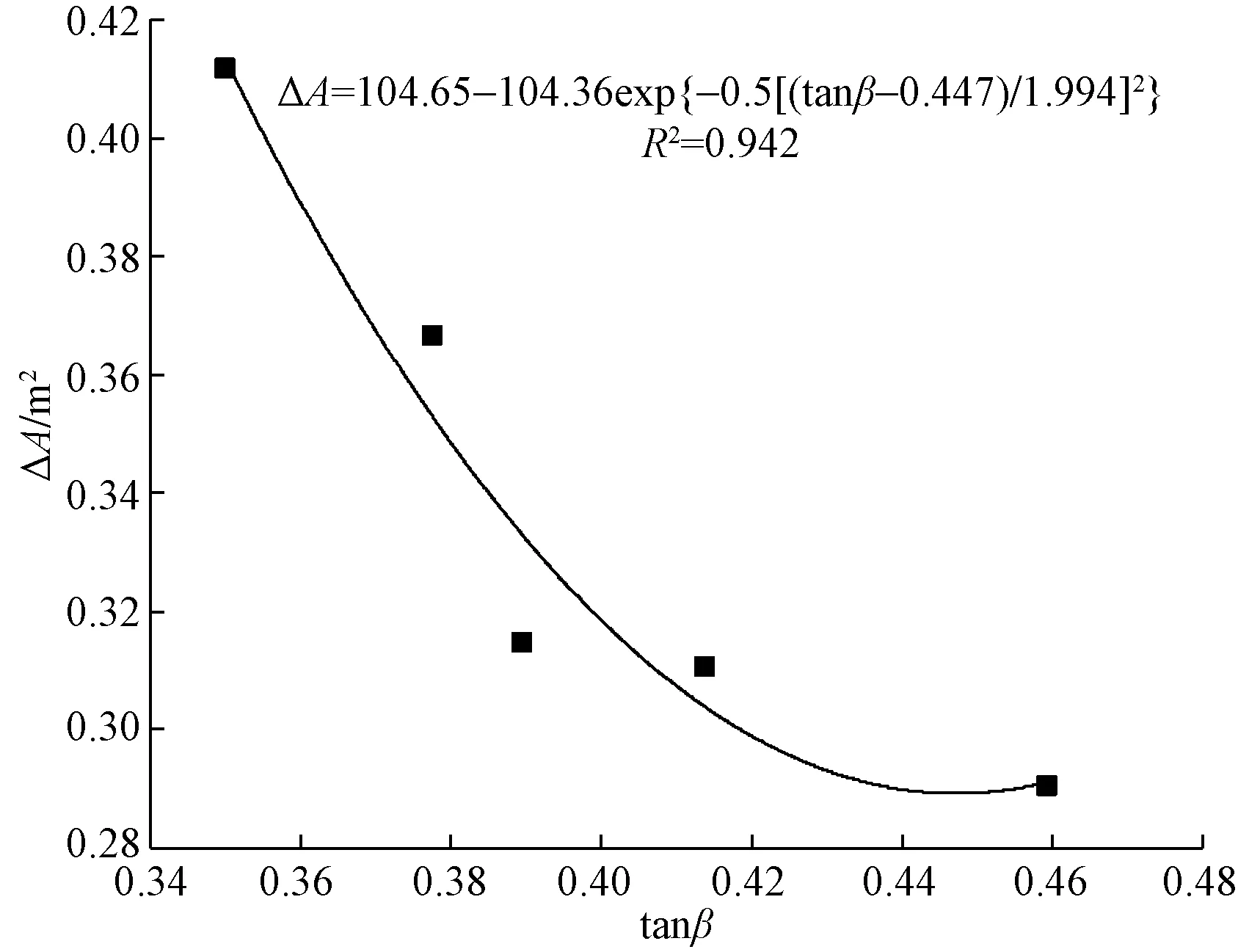
图12 ΔA与tanβ的关系图Fig.12 Relationship between ΔA and tanβ
如图12所示,随着地层影响角的正切值tanβ的增大,ΔA减小,且ΔA取值比较离散。当隧道埋深为20.53 m时,即ΔA接近0,此时tanβ为0.447。
4 基于BP神经网络的地表沉降预测分析
4.1 BP神经网络理论
1986年Rumel-hart和McCelland等人提出了反向传播(back propagation,BP)神经网络,具有模仿人大脑的功能,是一种误差反向传播神经网络。BP的主要目的是将各单元的信号误差值或残差值平均分配到各单元,不间断的调节各单元的权值,直到满足设定的训练次数为止。如图13所示为BP神经网络模型图。

图13 BP神经网络模型图Fig.13 Diagram of BP neural network model
4.2 BP神经网络预测模型建立
运用MATLAB2017b软件进行编程,通过滚动预测的方法建立BP神经网络预测模型。选取角山隧道DM-1断面从2021年5月30日—10月11日的地表沉降监测数据来预测未来的地表沉降趋势。将神经网络训练次数设置为100 000次,学习速率为0.01,训练目标最小误差为0.000 01,隐含层层数为5。将所有数据分为19组,每组由5个数据组成,其中前4个数据为输入样本,第5个为输出样本,组成的训练样本集合如表3所示。

表3 BP神经网络输入和输出数据Table 3 Input and output data of BP neural network
对样本进行训练并做出预测,D-6的预测沉降量与实际沉降量的对比图如图14所示。同时对DM-1断面各点的最终地表超小变形值进行预测,预测结果如表4所示。
在神经网络中常常利用均方误差(mean square error,MSE)、平方和误差(sum of squared error,SSE)和网络相关系数R来评价模型的好坏,网络相关系数R评价模型如图15所示。计算公式[20]为
(4)
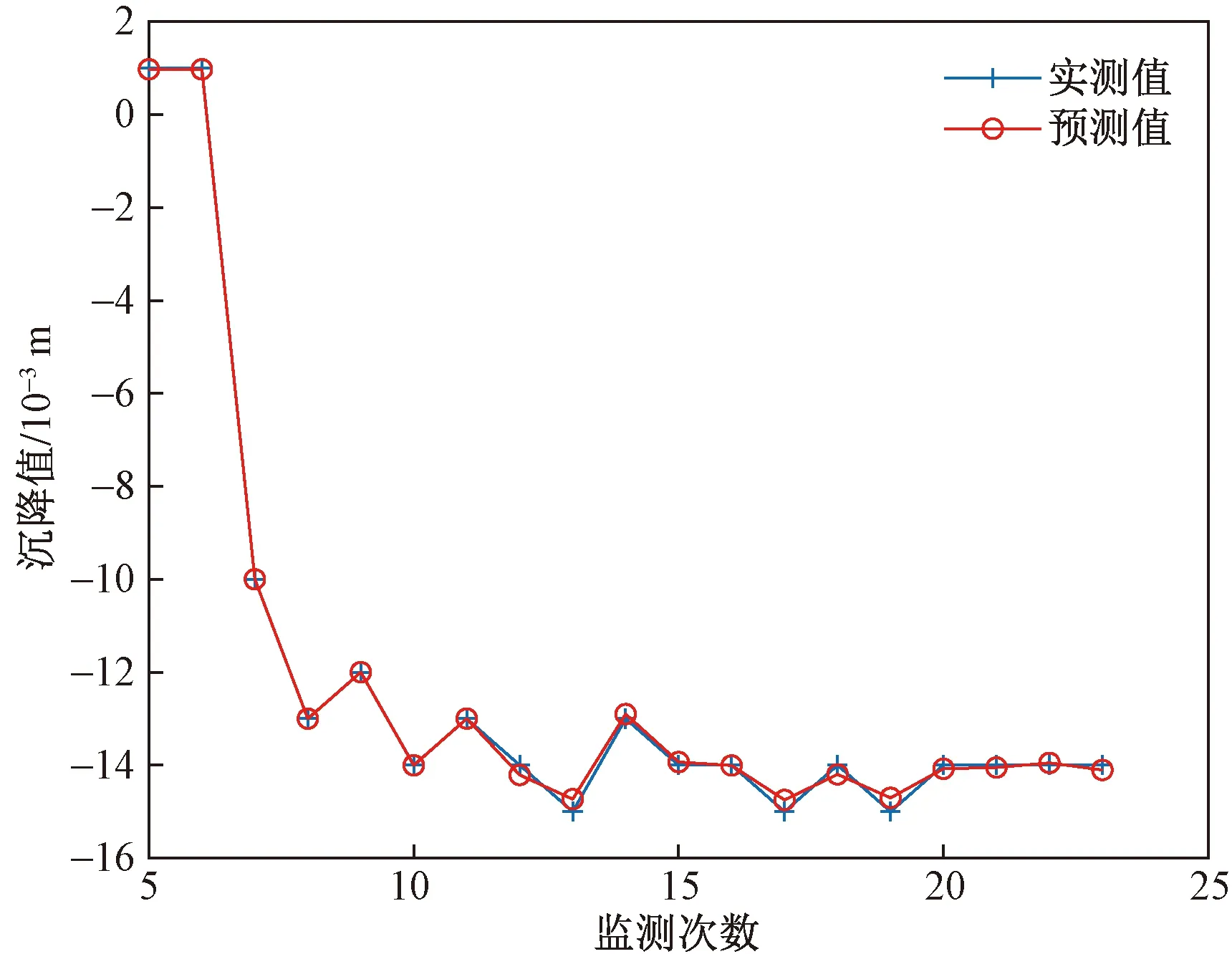
图14 预测沉降量与实际沉降量对比图Fig.14 Comparison between predicted and actual settlement amount

图15 BP神经网络相关系数RFig.15 Correlation coefficient R of BP neural network

表4 断面DM-1各监测点的最终沉降预测值及精度Table 4 Final settlement predicted values of monitoring points at section DM-1
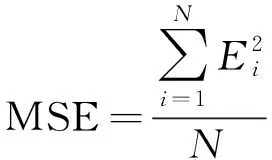
(5)
式中:Ei=Yi-Xi,Yi为预测值,Xi为实测值;N为样本总数。
由图14和图15可以看出,BP神经网络预测沉降与实际监测沉降结果相差较小,R达到了0.999 59,本次模型的MSE为1.81×10-8,SSE为3.44×10-7,拟合较好。根据式(4)和式(5)可以求出DM-1各点的MSE、SSE,表4所示为DM-1各点的精度表。
总体看来,建立的BP神经网络模型有很强的数据预测能力。而且每次预测的精度可以控制基本一致,误差较小,对于隧道的超小变形监测具有较好的工程指导意义。
5 结论
通过MATLAB进行反分析编程,利用实测的地表沉降数据,对随机介质理论中的两个主要参数隧道收敛面积ΔA和地层影响角β进行反分析,研究了在隧道地表超小变形下ΔA与tanβ以及ΔA与隧道埋深Z的关系。同时,通过滚动预测的方法建立BP神经网络模型,对角山隧道的未来地表超小变形值进行了有效预测。得到结论如下。
(1)在隧道开挖引起的地表超小变形下,隧道收敛面积ΔA随着隧道埋深的增加而逐渐减小,并且ΔA的取值比较离散,ΔA与隧道埋深大致呈ΔA=0.924-0.045Z的关系,当隧道埋深为20.53 m时,隧道收敛面积ΔA接近0。
(2)在隧道开挖引起的地表超小变形下,随着地层影响角的正切值tanβ的增大,隧道收敛面积ΔA减小,且ΔA取值比较离散,两者大致呈ΔA=104.65-104.36exp{-0.5[(tanβ-0.447)/1.994]2}的关系。当隧道埋深为20.53 m时,即ΔA接近0,此时tanβ为0.447。
(3)通过滚动预测的方法,建立BP神经网络预测模型,可以较好地预测地表未来的超小变形值。通过调节BP神经网络的相关参数对模型进行训练,可以使模型达到最优,并对角山隧道最终地表超小变形值进行了预测,对于隧道的超小变形具有较好的工程指导意义。
