层状岩体PFC模拟的细观参数分析
2023-02-11张龙飞孟江锋曹贺凯徐昭文李列列
张龙飞 孟江锋 曹贺凯 徐昭文 李列列
(华北水利水电大学土木与交通学院,河南 郑州 450045)
0 引言
在地质演化过程中,由于地层更替,构造运动,气候变化,海洋沉积等因素,天然岩体逐渐形成了含有不同方向、不同间距结构面的不连续岩体。该岩体在某一平面内的各方向物理力学性质相同(各向同性面),而垂直该面方向的物理力学性质却截然不同,因此具有这种性质的不连续岩体也可称为横观各向同性岩体[1-2]。
从细观力学角度来讲,岩石的损伤、扩容、变形、塑性屈服等均是由于微裂缝的成核和增大及其聚集而生成细观裂纹和裂纹的扩展与演化[3-5]。因此若能从细观力学角度来分析,并充分考虑岩体的非均质性,建立一种简单直接的数值模型来进行分析横观各向同性岩体的变形,破坏方式及其本构模型,这对横观各向同性边坡稳定分析、岩体地下工程及地下能源开采与储存均具有重要意义。随着数值理论及计算软件的发展,PFC2D(Particle Flow Code2D)在岩体细观研究领域得到成功应用,并取得了一些具有指导意义的研究成果[6]。
采用PFC2D模拟层状岩体时,可将其看成由完整岩石和一系列等间距层理组成的复合岩体,通过改变层理的倾角,以模拟层岩的各向异性力学特性,构建的模型通过细观参数的变化来展现岩体的非均质性,通过细观参数的变化,研究岩体的宏观力学参数的变化规律如图1所示。
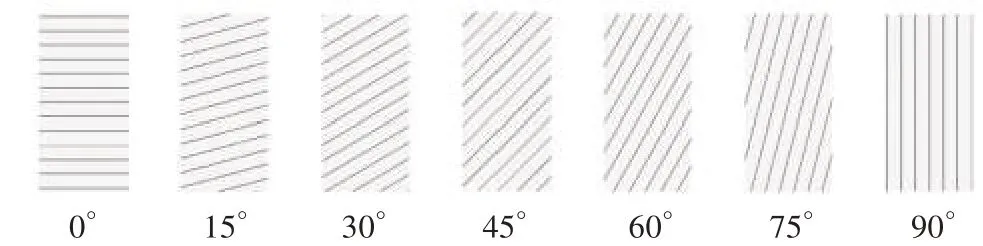
图1 层状岩体数值试件示意图
1 细观参数的敏感性分析
本研究选用岩石模拟中常用的平行黏结模型,前人研究表明,细观参数的取值与数值试件的宏观力学参数具有一定的关系。数值试件弹性模量主要受颗粒弹性模量和平行黏结弹性模量的影响,且成正比例关系;峰值强度主要受平行黏结法向强度和切向强度的影响,随着黏结强度的提高,峰值强度也随之升高;泊松比主要受颗粒的黏结法向刚度和切向刚度比值的影响,比值越大,泊松比越大,但是鲜有人研究细观参数对三轴力学特性的影响[7]。因此,本研究进行数值试件三轴压缩模拟,研究细观参数对黏聚力和摩擦角的影响。采用PFC2D生成宽(W)为50 mm,高(H)为100 mm的数值试件,并进行三轴压缩模拟,颗粒的基本细观参数如表1所示,如无特殊说明,颗粒间的黏结距离值均取0。

表1 基质细观参数
2 细观参数对力学性能的影响
2.1 颗粒半径的影响
颗粒半径是PFC2D数值试件的基本参数,选择试件的宽度(W)与平均颗粒半径(R)的比值(S=W/R)为10、20、30、50、100、150,其余细观参数取值如表1所示,分别进行三轴压缩模拟。模拟结果如图2所示。
由图2可以看出,当S从10增加到20时,黏聚力和摩擦角均急剧降低;当S从20增加到50时,黏聚力和摩擦角均出现上升现象;当S大于50时,黏聚力和摩擦角的变化幅度不大,基本稳定为一个恒定值。根据REV理论,采用PFC2D进行数值模拟时,试件的最小尺寸不得小于平均颗粒半径的50倍。
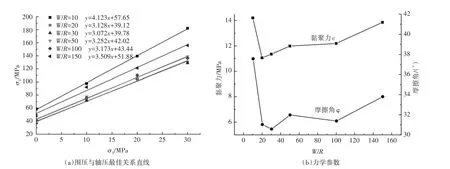
图2 不同颗粒半径试件的三轴数值模拟结果
2.2 摩擦系数的影响
为研究颗粒间摩擦系数对数值试件三轴力学特性的影响,分别取颗粒间的摩擦系数f为0.1、0.2、0.3、0.5、1.0、2.0、3.0、4.0,其余细观参数取值如表1所示,分别进行三轴压缩模拟。模拟结果如图3所示。
由图3可以看出,随着摩擦系数的增加,试件的摩擦角逐渐升高,上升速率逐渐降低,当摩擦系数大于2.0时,摩擦角趋于稳定;与此相反,随着摩擦系数的增加,试件的黏聚力逐渐降低,且下降速率逐渐降低,当摩擦系数大于2.0时,黏聚力亦趋于稳定。通过回归分析,黏聚力c和摩擦角φ与摩擦系数f的关系为式(1)、式(2)。
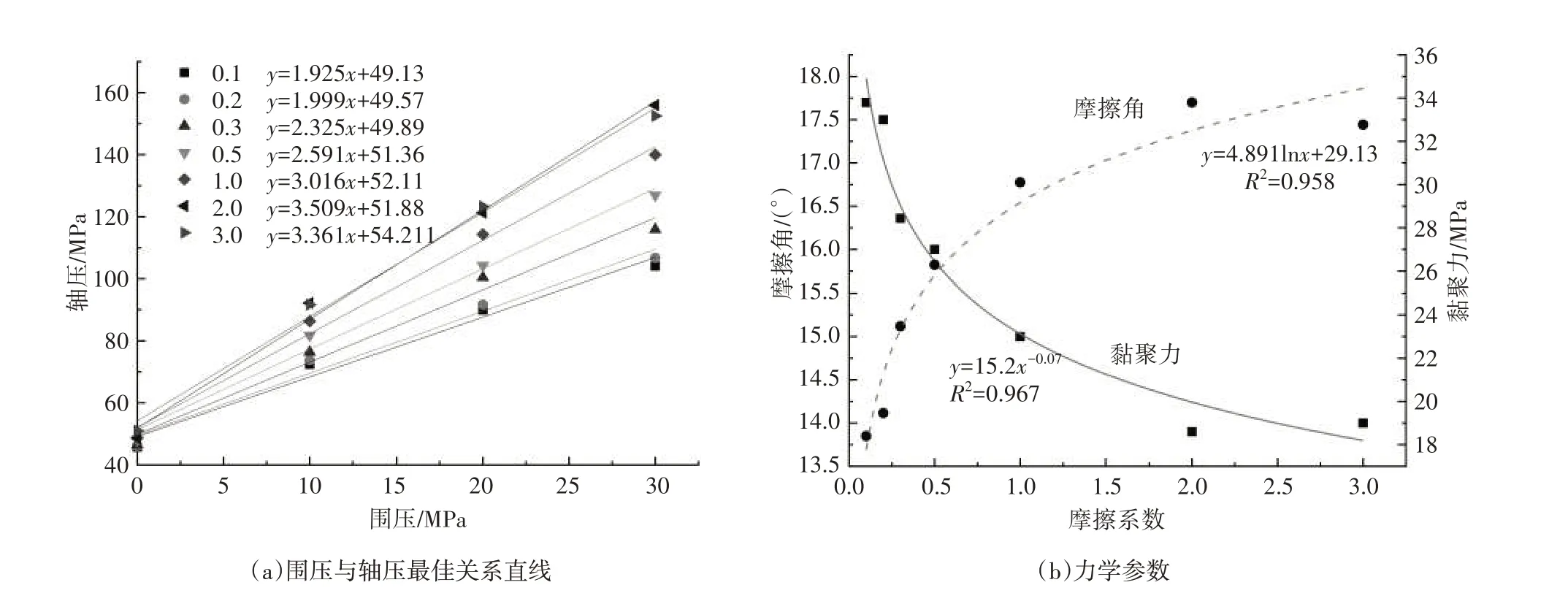
图3 不同摩擦系数的三轴数值模拟结果

2.3 黏结摩擦角的影响
为研究平行黏结摩擦角对数值试件三轴力学特性的影响,取平行黏结的摩擦角ϑ为0°、10°、20°、30°、40°、50°,其余细观参数取值如表1所示,分别进行三轴压缩模拟。模拟结果如图4所示。
由图4可以看出,随着黏结摩擦角的增加,试件的摩擦角呈现线性增加的趋势;与此相反,随着黏结摩擦角的增加,试件的黏聚力呈对数函数形式降低,且下降速率逐渐降低,通过对三轴试件的强度=回归分析,黏聚力c和摩擦角φ与黏结摩擦角ϑ的关系为式(3)、式(4)。
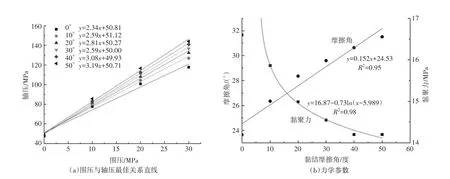
图4 不同黏结摩擦角试件的三轴数值模拟结果
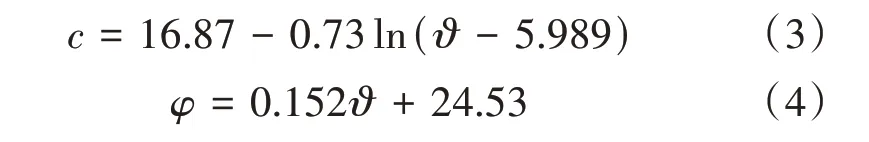
2.4 黏结距离的影响
在PFC2D模拟中,颗粒间距小于某一值时才会赋予平行黏结模型,一般情况下默认为零,为研究黏结间距对数值试件三轴力学特性的影响,取平行黏结的黏结距离为颗粒平均半径的百分数ω为0%、10%、20%、30%、40%、50%,其余细观参数的值如表1所示,分别进行三轴压缩模拟。模拟结果如图5所示。
由图5可以看出,随着黏结距离的增加,试件的摩擦角和黏聚力均呈线性关系增加。这主要是由于黏结距离的增加,使试件的黏结数量增加,颗粒之间的相互作用更加显著,从而使力学性能得到显著的提高。通过回归分析,黏聚力c和摩擦角φ与黏结距离ω的关系为式(5)、式(6)。

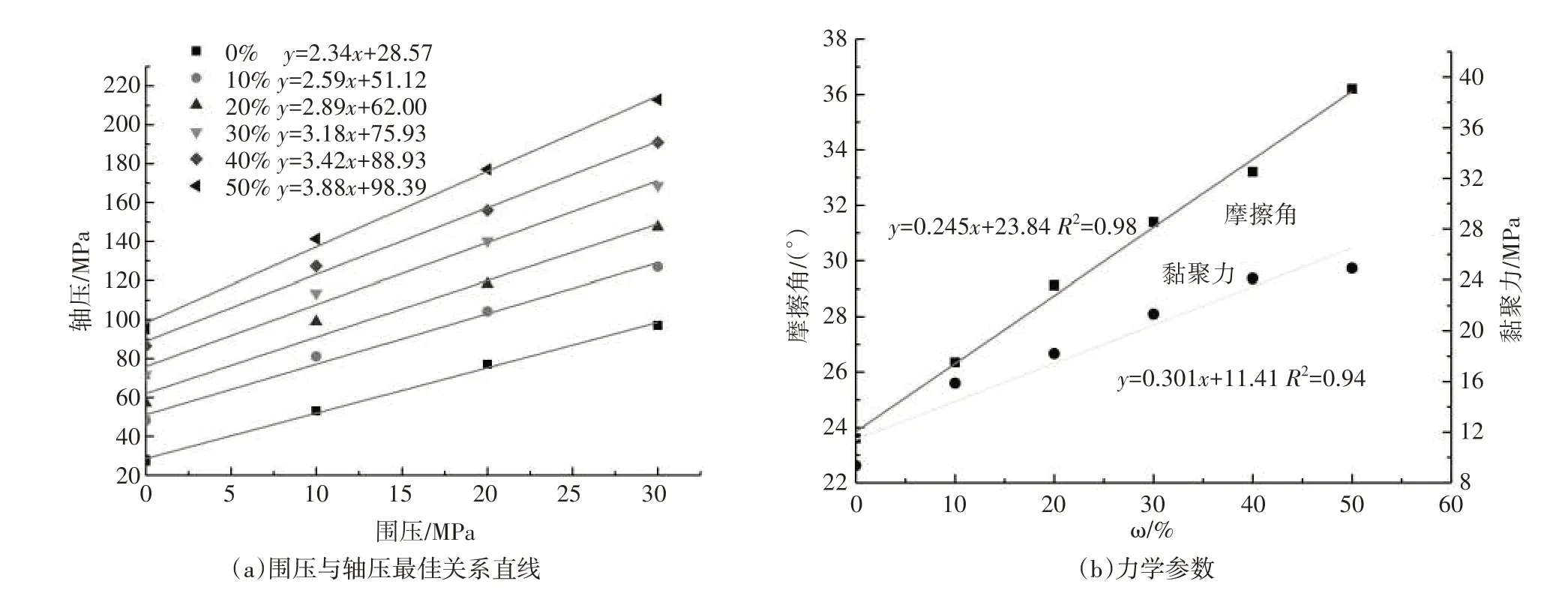
图5 不同黏结距离试件的三轴数值模拟结果
3 结论
采用PFC2D离散元数值分析软件,研究了细观参数对数值试件宏观力学参数的影响。基于复合岩体思想,在各向同性数值试件中加入不同倾角等间距的层理模拟层岩的各向异性,通过研究得到以下结论。
对三轴压缩下数值试件细观参数与宏观力学参数的关系进行了敏感性分析。数值试件的摩擦角随着颗粒间摩擦系数和黏结摩擦角的提高分别呈非线性以及线性增加趋势;数值试件的黏聚力随着颗粒间摩擦系数和黏结摩擦角的提高而呈非线性降低趋势;随着黏结距离的增加,数值试件的摩擦角和黏聚力均呈线性增加趋势。
