近树木条件下高压架空输电线路电场特性研究

刘海宁，何梓麟，何 康，覃远铖，唐金锐

（1.广东电网有限责任公司广州供电局，广州 510620；2.武汉理工大学 自动化学院，武汉 430070）

0 引言

随着高压输电工程的持续推进，一些高压架空输电线路不可避免地跨越植被覆盖区域。当线路走廊内的树木生长到一定高度时，其尖端与输电线路之间形成极不均匀电场而发生电晕放电现象，导致树木被灼烧［1］，甚至会诱发树闪故障，导致线路停电，从而影响供电可靠性［2-6］。据不完全统计，2015 年10 月南宁电网10 kV 及以上线路共跳闸160 条次，引发59 条线路因故障停运，停电影响居民户数29万余户，其中超过90%的事故由超高树木引起，这表明线路走廊内的超高树木已经严重威胁到了电网的安全稳定运行。因此，研究树木附近架空输电线路的电场分布特性具有重要意义。

国内外学者就树木对线路周围电磁环境的影响开展了相关研究。文献［7-9］通过仿真分析树木后方电场的分布特性验证了树木对地面电场的屏蔽效应，为种植树木以改善线路周围的电磁环境提供了理论基础；文献［10］通过实测树木附近的电磁参数，建立了树木在夏秋季的等效模型，并基于有限元法分析了线路走廊内树木屏蔽效应对线路电磁环境的影响，但对树木后方电场的研究并不能完全反映树木对线路电磁环境的整体评价。为此，一些学者对树木邻近架空输电线时的电场分布特性展开研究。文献［11］通过现场试验确定了30种阔叶乔木与±800 kV直流输电线路的最小净空距离；文献［12］基于上流有限元法仿真分析了树木邻近±1 100 kV 特高压直流输电线路时的电场分布特性；文献［13］将树木看作良导体，基于有限元法仿真分析了110 kV 交流输电线路下不同类型树木高度、位置和电源相角变化对电场分布的影响。除有限元法外，模拟电荷法也常被用来分析输电线路的电场分布特性。文献［14］通过点电荷与线电荷相结合的模拟电荷法分析了500 kV超高压输电线下方存在树木和建筑时的工频电场分布，然而其并未对树木邻近输电线时的电场分布特性展开研究。确定模拟电荷位置是在复杂场景下应用模拟电荷法的难点所在，为此文献［15］提出用蜂窝状网格划分建筑物表面的改进方案，该方案减少了23%的模拟电荷，在一定程度上提高了运算效率。以上方法均对模拟电荷法进行了改进，为分析实际场景下工频电场分布提供了一些便利。但在处理复杂场景、尤其是在物体边界和曲率变化大的区域，匹配点和模拟电荷的空间坐标难以确定，如何快速地对模型中模拟电荷和匹配点进行配置还有待进一步研究［16］。

本文采用模拟电荷法分析树木附近架空输电线路的电场分布特性，分别采用变步长划分和有限元网格剖分的方法对输电线路和树木模型中的模拟电荷和匹配点进行配置；利用有限元仿真结果验证了本文所使用的模拟电荷法的可行性；讨论了输电线路下方树木的数量、疏密程度、位置和高度对电场分布的影响，并确定了本文案例中树木与500 kV超高压交流输电线路的最小净空距离。

1 仿真模型及理论分析

1.1 仿真模型

近树木条件下高压架空输电线路等效模型如图1所示。输电线路下方地势平坦，三相导线和地线均呈水平排列；输电线路模型为四分裂导线，型号为LGJ-400/45；子导线半径14.8 mm，分裂间距400 mm，相邻导线间距12 m，导线最低点离地高度为20 m；架空地线型号为GJ-70，半径5.5 mm，相邻地线间距10 m，地线与导线之间的垂直距离为6 m。

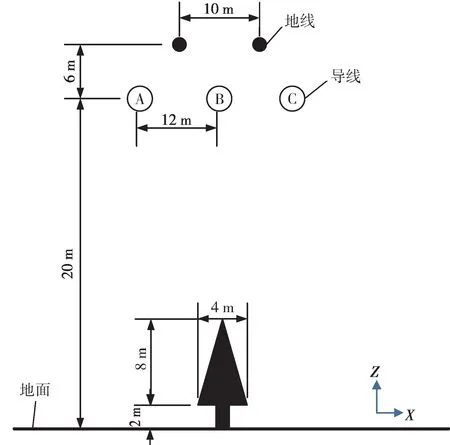
图1 高压架空输电线路和树木等效模型Fig.1 An equivalent model of high-voltage overhead transmission lines and a tree

在架空输电线路走廊内，导线最低点附近的树木更容易发生电晕放电和闪络，文中仅考虑档距中央附近树木的电场分布特性。此时，位于档距中央的树木与铁塔的距离一般在200 m以上，可以忽略铁塔、绝缘子和金具的影响。本文计算区域区间的大小和输电导线的距离已经远远大于分裂导线之间的几何尺寸。将分裂导线等效为单根导线，可在保证电场计算结果准确的前提下提高计算效率。单根导线的等效半径可由式（1）求得：

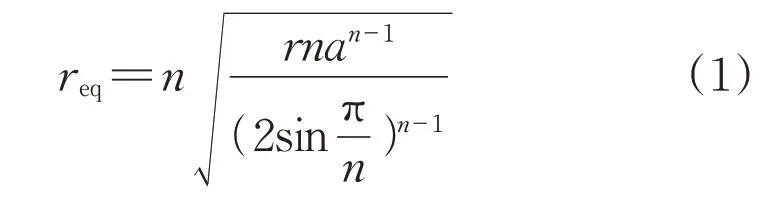
式中：n为导线分裂数，n≥2；r为子导线半径；a为子导线分裂间距。

研究表明，相较于椭圆体和球体树冠，圆锥体树冠造成电场的畸变程度更大［13］，能更好地反映严酷条件下的电场分布规律，因此本文选取树冠呈圆锥体的树木作为研究对象。建立树木模型时做了如下简化：树干等效为高度2 m、半径0.2 m的细长圆柱体；树冠等效为高度8 m、底面半径2 m的圆锥体。在工频电压作用下，树木的电导率一般在10-5～10-3S/m，相对介电常数一般在103～105［17］，将树木视为良导体，其表面电势为0。

1.2 模拟电荷法计算理论

与有限元法相比，模拟电荷法计算静电场时无需封边，具有未知量少、求解速度快和准确度高等特点，非常适合求解开域静态场问题，已广泛应用于架空输电线路下方的电场计算。模拟电荷法的基本原理是：用一组人为布置在场域外的离散电荷来代替连续分布在电极表面的自由电荷与存在于介质表面的约束电荷，基于静电场中的唯一性原理，通过假设模拟电荷满足边界条件来求解整个场域内的电位和电场［18-21］。导线结构简单，则选择单位线电荷作为模拟电荷；树木形体复杂，则选用适量数目的点电荷作为模拟电荷。故采用线电荷与点电荷相结合的模拟电荷法，通过式（2）—（3）计算待求模拟电荷量。

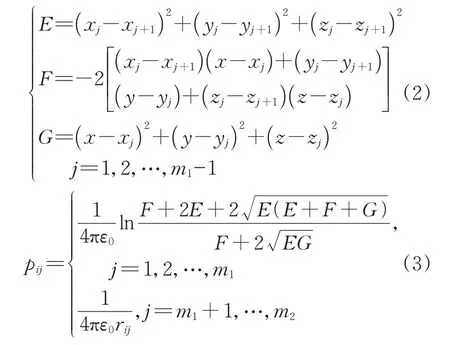
式中：pij为第j个模拟电荷对第i个匹配点的电位系数；m1为输电线路中模拟电荷总数；m2为场域中模拟电荷总数；rij为第j个模拟点电荷和第i个匹配点之间的距离；（xj，yj，zj）为第j段模拟线电荷端点的起始坐标；（x，y，z）为待求点的坐标。

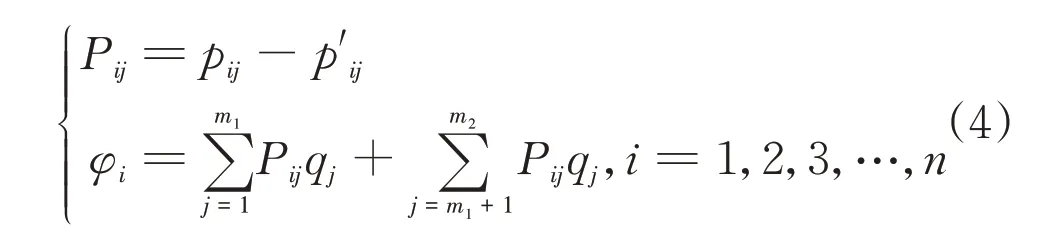
式中：p′ij为第j个模拟电荷相对应的镜像电荷对第i个匹配点的电位系数，求法同式（3）；φi为第i个匹配点上已知边界电势；qj为第j个待求模拟电荷量；n为匹配点总数。

第j个模拟电荷对场域内任意一点（x，y，z）产生的电场强度在X轴上的分量Exj为：

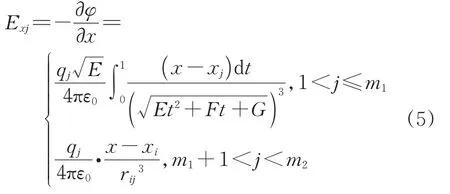
同理可以计算出Eyj与Ezj。根据叠加原理，场域内任意一点的电场强度在x、y、z3个方向的分量和场域中任意一点的电场强度为：

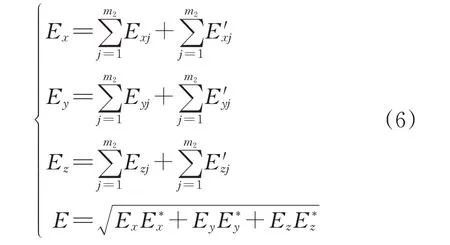
1.3 模拟电荷配置方案

在确定了模拟电荷类型和电场计算方法的基础上，还需确定输电线路与树木模型中模拟电荷的配置方案。模拟电荷的配置将直接影响到空间电场计算结果的准确性，输电线路与树木的几何结构和所使用的模拟电荷类型存在本质差异，故对两者需要采取不同的配置方案。

在配置导线和地线的模拟电荷时，可将导线分成若干段圆柱体微元，在圆柱体微元轴线和表面上分别设置单位线电荷和适量的匹配点、校验点，由此将复杂结构的电场计算问题转化为圆柱体微元表面电位匹配问题。电场计算的精度与划分步长相关，圆柱体划分得越细，电场计算越精准，但电位矩阵的阶数也会成倍增加，降低计算效率。本文采用变步长划分的方法将导线和地线分别划分成N段，如图2所示，导线上靠近关注区域的位置采用较小步长来划分，以提高关注区域内电场计算的精度；远离关注区域位置上的电荷对电场贡献小，则用较大步长来划分。

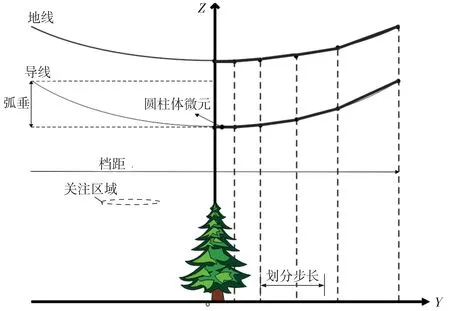
图2 模拟线电荷划分示意图Fig.2 Schematic diagram of charge division on analog lines

树木等效模型中模拟电荷的配置难点在于模拟电荷位置的确定。传统方法采用等间距的纵横线分割模型，将模拟电荷和匹配点放置在横竖线的交点处［14］。但在处理复杂模型时，传统方法难以获得模拟电荷和匹配点的空间坐标，更无法控制模拟电荷的布置密度，存在明显的局限性。本文提出一种基于有限元网格划分确定复杂模型中模拟电荷和匹配点的分布特征的方法。在有限元仿真软件中对树木模型进行网格剖分，并提取网格节点的信息，从而获得模拟电荷和匹配点的空间坐标以及布置密度。在处理复杂模型时，该方法能够快速获得模拟点电荷和匹配点的空间坐标，优势明显。树木模型中网格剖分、模拟电荷以及匹配点的配置方案如图3所示（以高度为10 m的树为例，匹配点的数量为617个）。

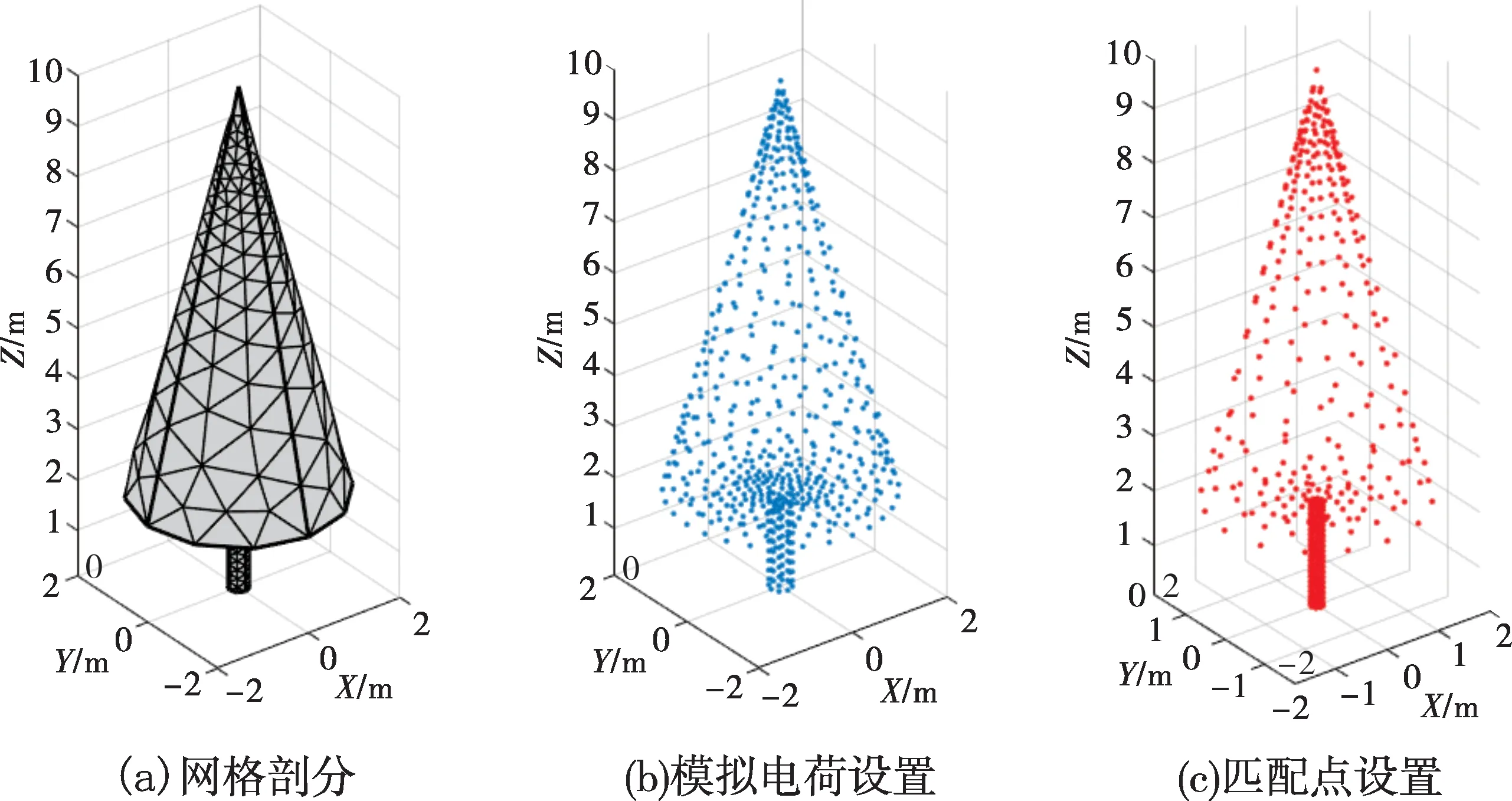
图3 树木网格划分及模拟电荷、匹配点配置示意图Fig.3 Schematic diagram of tree meshing，simulated charges，and matching point configuration

在建立树木模型时，圆锥体树冠头部被设置成小曲率抛物面，并在抛物面的焦点处设置点电荷来控制抛物面顶点电位以优化计算结果［20］。模拟电荷对其附近区域的电场有重要影响，由于本文主要关注的区域位于树木上方，故树木顶端的模拟电荷设置得较密，树冠底部和树干上的模拟电荷设置得较稀疏。

1.4 计算方法验证

本文使用有限元计算软件验证模拟电荷法的计算结果。由于输电线路走廊长、导线结构尺寸小，有限元计算时会存在低质量网格和内存溢出的问题，需要对模型进行简化处理。输电线路长度为200 m，四分裂导线等效为单根导线，忽略地线、杆塔和金具的影响；求解区域设置为半径50 m、高200 m的半圆柱体；树木的电导率设为0.001 S/m，相对介电常数设为5 000。以一棵树为例，将其布置在档距中央截面中心导线正下方，并定义此处为中心点，沿着导线架设方向在树木的上方和下方各取1条路径作为验证路径，将有限元仿真结果与模拟电荷法计算结果进行比较，结果如图4 所示。由图4可知，2条验证路径的有限元仿真结果与模拟电荷法计算结果吻合良好，表明将树看作良导体是可行的，验证了本文三维电场计算方法的准确性。

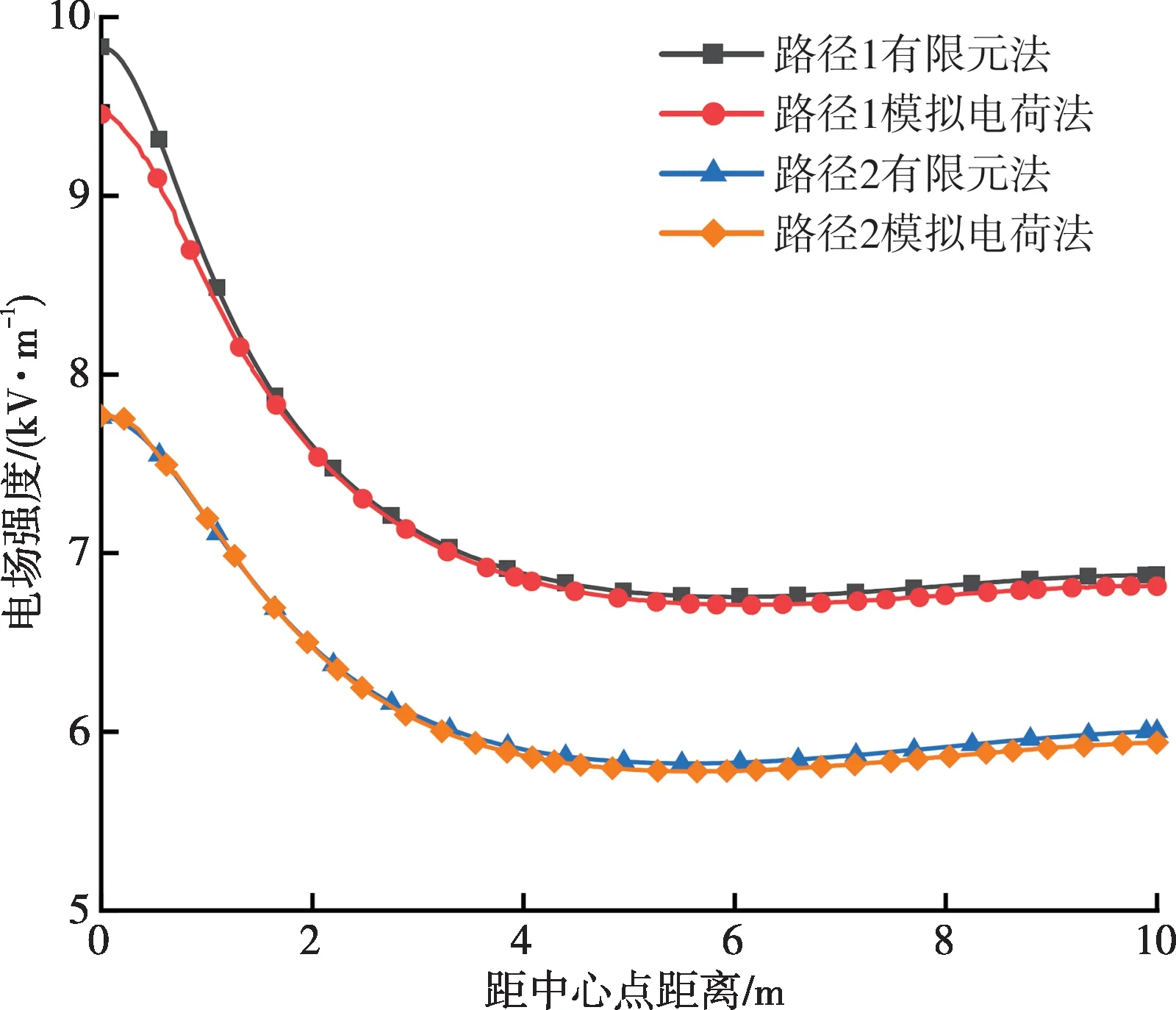
图4 计算路径电场强度仿真结果对比Fig.4 Comparison of simulation results of the electric field strength on calculated paths

2 电场分布特性

高压输电线路邻近树木时，树木附近的电场分布与树木数量、位置、高度及种植密度等因素相关，下面就这些因素展开讨论。因在分析树木数量、位置和种植密度对电场分布的影响时，树的高度均为10 m，与导线的净空距离为9.8 m，在这个距离下，导线-树木间隙不会发生放电，所以导线施加的激励是电压的有效值，以此来表示电压长期作用下树木上方的电场分布规律；而在分析树木高度这一影响因素时，主要目的是求出导线-树木间隙不发生放电时的最小净空距离，间隙放电极有可能发生在电压的峰值时刻，所以讨论树木高度这一影响因素时导线施加的激励是电压峰值［22-23］。

2.1 树木数量及种植密度对电场分布的影响

线路走廊内的树木往往不是单独存在的，树木随机分布性强，因此有必要讨论树木数量及种植密度对输电线路电场分布的影响。假设各树木的模型及参数相同，将线路中心点上的树木设置为参考树木，相邻两棵树轴线之间的距离为4 m，通过改变围绕在参考树木周围的树木数量来研究电场分布的变化。本文选择的计算路径如图5（a）所示，2 条路径位于中心点树木上方0.5 m 处，2条路径的交点定义为参考点。在中心点周围分别布置了1、3、9、25 棵树进行电场计算，其中“3棵树”沿“路径1”对称分布在中心点的两侧，9棵和25棵树均匀分布在中心点的四周。

2条计算路径上的电场强度分布如图5（b）、图5（c）所示。可以看出，树冠上方的空间电场发生了严重畸变，畸变后的电场分布关于参考点对称；随着树木数量的增加，树冠上方的电场强度逐渐减小；当输电线路下方仅存在单颗树木时，参考点的电场强度最大。

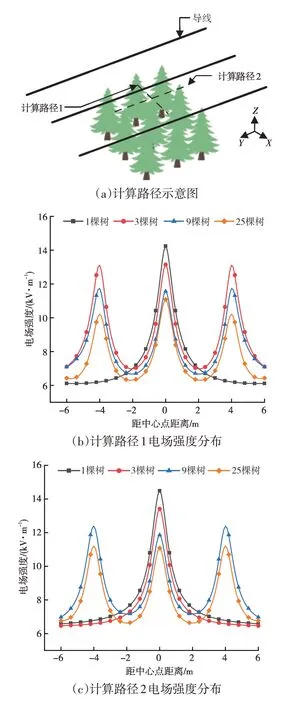
图5 计算路径电场强度分布Fig.5 Electric field strength distributions on calculated paths

不同树木数量时参考点处的电场强度见表1。可以看出，随着种植数量的增加，电场强度的降幅分别为7.45%、13.8%和4.15%，降幅呈现先增大后减小的趋势，表明树木数量增长到一定程度时，继续增加其数量对电场分布的影响程度减小。

表1 不同树木数量时参考点处电场强度Table 1 Electric field strength values at reference points under different numbers of trees

通过改变相邻树木之间的距离来体现不同的种植密度，以9棵树木为例，相邻树木之间的距离L分别设置为2 m、4 m、6 m和8 m，得到计算路径1上的电场强度分布如图6所示。可以看出，随着树木间距的变化，电场极大值出现的位置也发生了变化，极大值始终出现在每个树冠的上方，极小值出现在相邻树木之间；参考点处的电场强度随着种植密度的增大而减小。

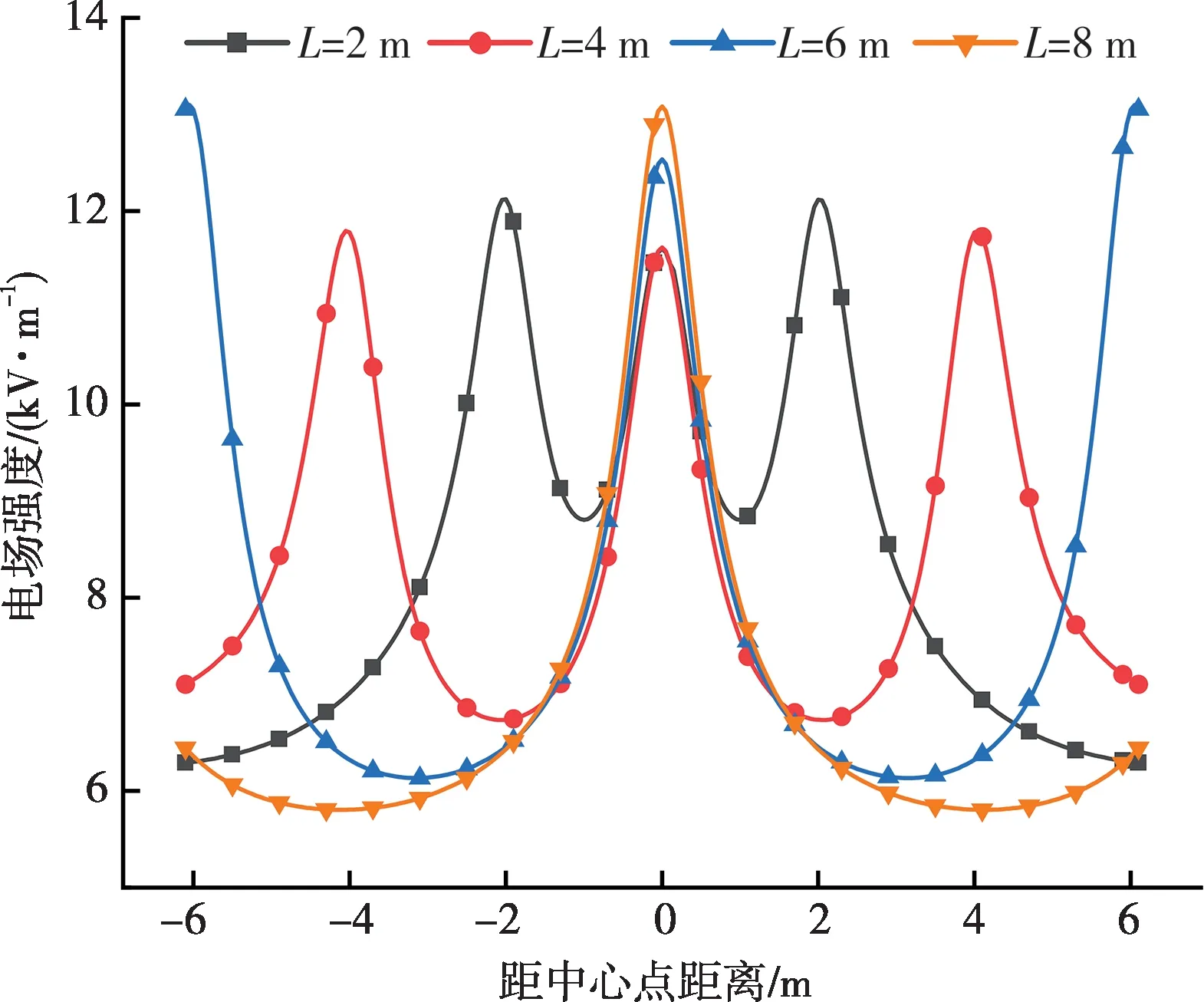
图6 不同树木间距下电场强度分布Fig.6 Electric field strength distributions under different tree spacing

不同树木间距下参考点的电场强度如表2 所示。可以发现，随着种植密度的增加，电场强度的降幅分别为4.13%、7.81%和0.17%，降幅总体呈下降的趋势，表明当种植密度增加到一定程度时，继续增大种植密度对参考点附近的电场强度的影响很小。

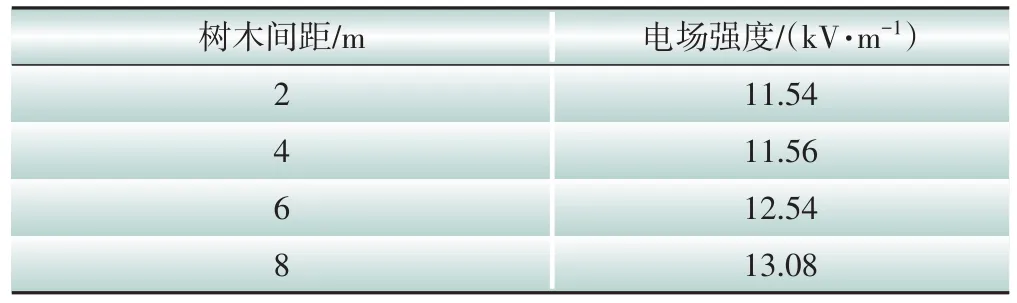
表2 不同树木间距下参考点电场强度Table 2 Electric field strength values at reference points under different tree spacing

2.2 树木位置对电场分布的影响

以1棵树木为例，将树木从中心点分别沿X轴（垂直线路走廊方向）和Y轴（线路走廊方向）正方向移动（移动距离d分别设置为0 m、4 m、8 m、12 m、16 m），研究不同树木位置对树冠上方电场强度的影响（此时计算路径选取的是树木上方0.5 m 处沿X轴方向以树木轴线为中点的长12 m 的线段）。计算结果如图7 所示，可以看出：无论沿着X轴还是Y轴移动，树冠上方的电场强度均发生了明显畸变，最大场强均出现在树冠尖端上方；当树木沿X轴移动时，计算路径上的电场不再呈对称分布；当树木沿Y轴方向移动时，计算路径上的电场强度随着移动距离的增加而略有减小。

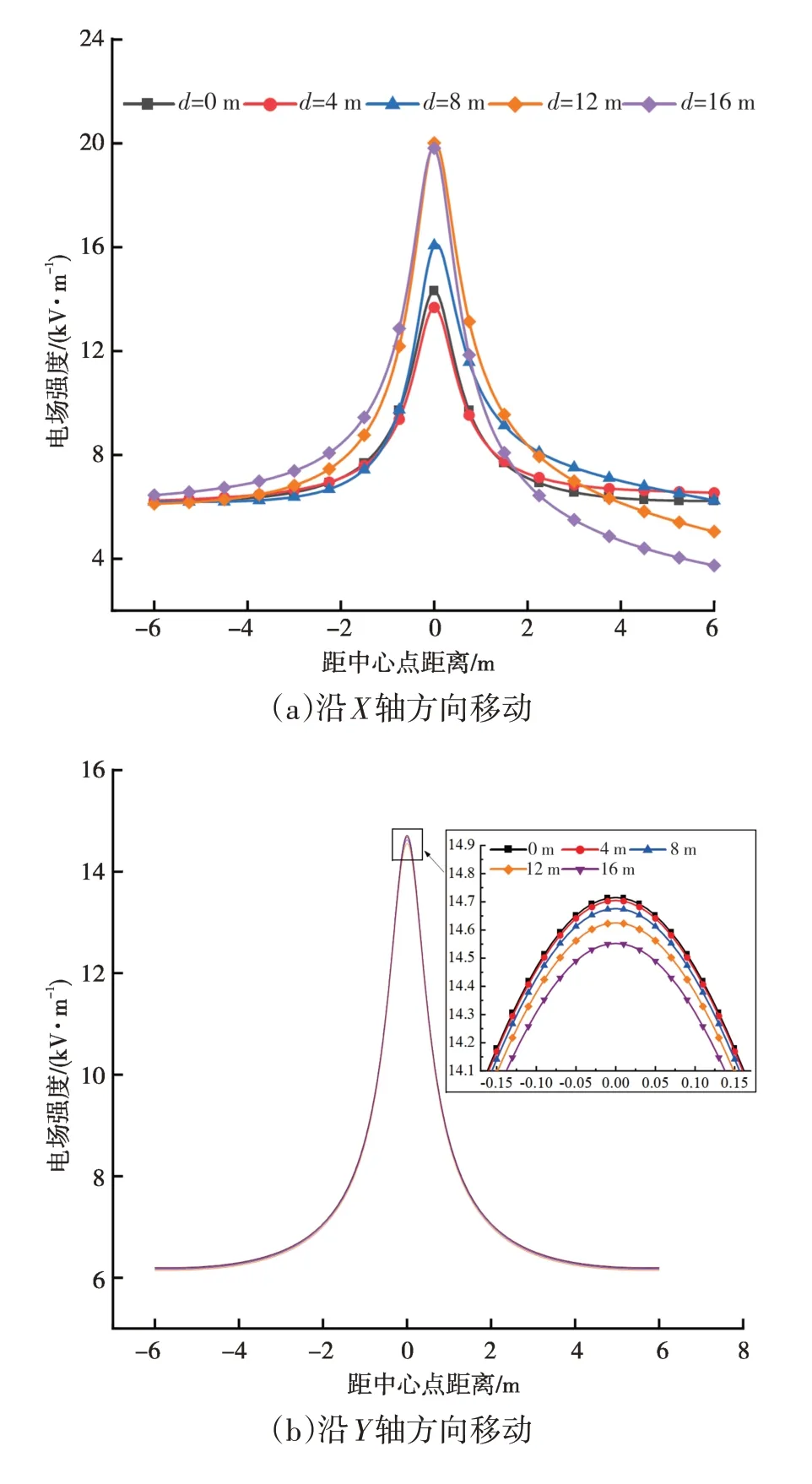
图7 不同移动距离下计算路径上的电场强度分布Fig.7 Electric field strength distributions on the calculated path at different moving distances

树冠尖端上方的电场强度随树木位置变化的结果如图8 所示。在树木沿X轴方向水平移动的过程中，电场强度先缓慢减小，当移动距离为4 m时有最小值；继续增加移动距离，电场强度迅速增大，移动距离为14 m 时电场强度达到最大值20.5 kV/m。当树木沿Y轴方向水平移动时，电场强度随着移动距离的增加以极小的幅度线性减小。

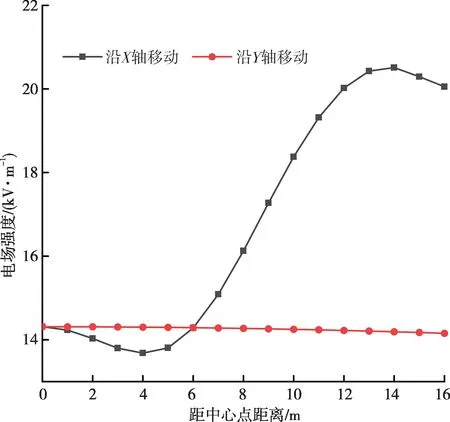
图8 不同移动距离下树冠尖端上方电场强度分布Fig.8 Electric field strength distributions above the crown tips at different moving distances

2.3 树木与输电线路之间的净空距离

导线与树木之间的电场与极不均匀电场相似［24］，可用极不均匀电场的击穿过程进行分析。在间隙距离较小时，棒-棒间隙工频击穿电压与间隙距离呈近似线性关系，平均电场强度在4～6 kV/cm。考虑较为严峻的情况，取平均电场强度4 kV/cm作为导线-树木间隙击穿的判据。

在同等高度情况下，档距中央截面上的电场强度比其他截面更大，因此，树木与输电线路之间的安全距离可通过最短路径的平均电场强度判定，其中最短路径定义为导线与树冠尖端的最短距离。以1 棵树为例，将其布置在档距中央中心导线下方，通过改变树木与导线的净空距离，得到最短路径上电场分布，如图9所示。由图9可知，导线-树木间隙最短路径上的电场分布近似为“U”形，这与棒-棒间隙最短路径上的电场分布是相似的。

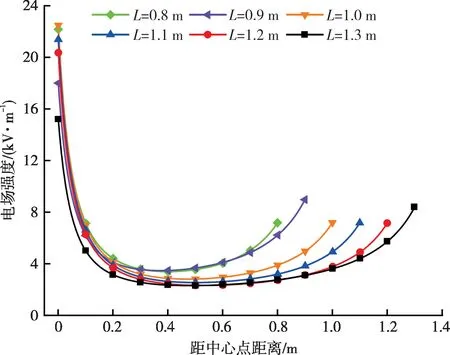
图9 不同净空距离下最短路径电场分布Fig.9 Electric field distributions on the shortest path at different clearances

在计算两电极间的平均电场强度时，通常用电极电压除以间隙距离得到：

式中：U为电极所加电压；d为间隙距离。

但本文中导线-树木间隙最短路径上的平均电场强度是三相导线共同作用的结果，难以用导线电压除以间隙距离来表示最短路径上的平均场强。本文使用的方法是在最短路径上每0.001 m取一个采样点，将所有采样点电场强度的平均值作为该净空距离下最短路径上的平均电场强度：

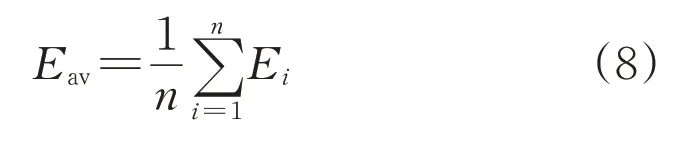
式中：Ei为第i个采样点的电场强度；n为采样点的总数。

根据式（7）、式（8）计算得到的不同净空距离下最短路径上的平均电场强度，如图10 所示。可以看出，两种计算方法的最大误差不超过20%，并且式（8）计算的平均值要大于式（7）。考虑留有更大的安全裕度，选用式（8）的计算结果更为合适。

图10 的计算结果表明：当树木与导线的净空距离分别为1 m和1.2 m时，最短路径上的平均电场强度为4 kV/cm；净空距离为1.2 m 时比1 m 时留有的安全裕度更大。因此，为保证输电线路安全运行，树木与导线的距离应大于1.2 m。

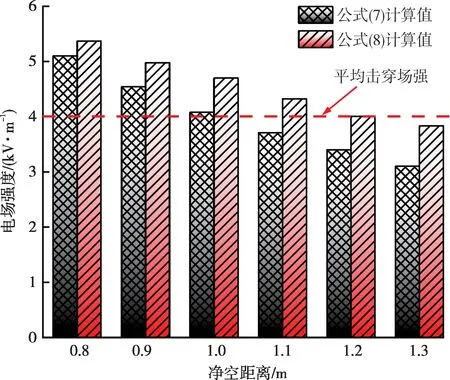
图10 不同净空距离下最短路径平均电场强度Fig.10 Average electric field strength on the shortest path at different clearances

3 结论

1）在工频电场作用下，可将树木视为良导体，分别采用变步长和有限元网格剖分的方法对导线和树木模型中的模拟电荷及匹配点进行配置，并通过有限元仿真验证了该配置方案的可行性（该方案在处理复杂模型时具有未知量少、求解速度快和准确度高的优势）。

2）当呈水平排列的500 kV 输电线路走廊内存在树木时，树木上方的电场会发生明显的畸变，导线档距中央截面中心导线下方的电场强度随树木数量和种植密度的增加而减小。

3）当树木在500 kV 输电线路档距中央处的位置由中心导线向边相导线移动时，树冠上方0.5 m处的电场强度先缓慢减小后迅速增大，在移动距离为14 m 时达到最大值20.5 kV/m；树木沿输电走廊方向水平移动时，电场强度随着移动距离的增加而以极小的幅度线性减小。

4）将树木布置在导线档距中央截面中心导线正下方时，通过改变树木与导线的净空距离，观察最短路径平均电场强度的变化，确定了树木与500 kV输电导线之间的最小净空距离为1.2 m。