考虑车主多模式需求响应模糊意愿的优化调度策略

李咸善，周晓岚，姚俊伟，谢琼瑶

考虑车主多模式需求响应模糊意愿的优化调度策略

李咸善1,2，周晓岚1,2，姚俊伟3，谢琼瑶3

(1.梯级水电站运行与控制湖北省重点实验室(三峡大学)，湖北 宜昌 443002；2.三峡大学电气与新能源学院，湖北 宜昌 443002；3.国网宜昌供电公司，湖北 宜昌 443002)

现代电动汽车(electrical vehicle, EV)用户需求响应具有多样性和意愿模糊性的特点，当实施单一激励政策时，EV响应将达不到预期效果。为此，提出了考虑车主多模式需求响应及其模糊意愿的含EV微电网的主从博弈优化调度策略。微电网主体针对净负荷制定多模式动态电价激励政策，引导EV在多模式电价中做出选择，促进EV有序充放电，实现其净负荷均方差和运行成本最小。车主从体基于模糊逻辑推理意愿决策，响应多模式动态电价，极小化车主成本。采用非支配排序遗传算法(NSGA-Ⅱ)求解优化模型，获得最优多模式动态电价和EV充放电策略。仿真结果验证了所提方法的有效性。

主从博弈；车主意愿；多模式响应；动态电价

0 引言

电动汽车(electrical vehicle, EV)凭借其绿色、环保等特点迅猛发展，保有量逐年攀升。对于含EV的微电网来说，电动汽车充放电行为的随机性和无序性加剧微电网负荷的波动性，出现“峰上加峰”、“反调峰”等现象[1-2]，增加了微电网优化调度的难度。借助不断成熟的电动汽车入网技术，通过需求响应实现EV与微电网的良性互动将有助于促进“车-网”系统的安全高效运行。

目前代表性的研究成果是电网实施分时电价激励政策，可有效引导EV有序充放电，实现电网的削峰填谷调度目标。前提条件是所有EV车主愿意按照分时电价引导参与响应。考虑到EV用户消费需求的提升及消费价值观的多样化，EV参与电网调度的需求响应模式呈现差异性和多样性，参与意愿具有模糊性。在此背景下，实施单一模式的分时电价激励，EV响应将达不到预想效果甚至更加恶化。

多数电动汽车一天内的大部分时间处于空闲状态[3]，因而均有可能通过需求响应参与到微电网的调峰调度中来。EV用户需求响应可分为3种典型模式：即充即走(模式一)，仅参加充电调度(模式二)，参与充放电调度(模式三)。EV车主选择这3种模式的意愿与车主的性格及模式价格等因素有关，具有模糊性。针对上述EV的需求特点，微电网需要制定相应的激励政策，引导EV有序充放电，减小净负荷波动，提升系统整体效益。为此，本文将重点研究考虑EV多模式需求响应及车主模糊意愿的含EV微电网系统的优化调度策略，达到“削峰填谷”效果，实现车主和微电网主体的利益共赢。

目前，在EV参与电网调度的模式研究方面，主要采用集中调度[4-5]和分层调度[6-7]的方式，没有考虑不同车主需求响应的差异性。文献[4]综合分析已入网汽车的确定信息和未入网汽车的预测模型来预测电动汽车集群充电行为，再通过滚动优化确定入网EV的实时充电功率，达到更好的填谷效果。在文献[5]中，微电网调度中心根据网内新能源和负荷的功率差值，发布电价信息调动EV有序充放电来平缓等效负荷曲线。文献[6]采用双层调度模型，下层EV代理商通过设置惩罚系数来控制EV各时段的充放电状态，以此响应上层调度机构制定的充放电策略。文献[7]建立了一个含EV、EV调度机构和配电中心的3层调度架构，通过EV响应电价、EV 调度机构调整充放电计划和控制中心实时更新分时电价的方式引导 EV 充放电。但是上述文献对于全体电动汽车采取同样的调度策略，没有考虑不同车主需求响应的差异性。

在微电网的激励政策方面，目前的研究主要通过电价激励政策引导电动汽车的有序充放电。文献[8]构建不同舒适价格的电动汽车充放电行为优化模型，文献[9]采用基于主从博弈更新的分时电价，文献[10]采用基于合作博弈得到动态分时电价激励。以上文献表明，分时电价模式对引导 EV 有序充放电具有重要的作用，相比于静态分时电价，动态电价削峰填谷的效果更加明显。这些文献针对不同类型的车主采用同样的激励政策，没有考虑EV参与需求响应模式的差异性和多样性。

目前关于电动汽车入网的研究大多直接设计调度策略，对于车主参与调度的意愿研究较少，且主要集中于充放电调度意愿和出行满意度的考虑，而对于现代消费方式下，车主自身参与不同需求响应模式的意愿的考虑还鲜有文献研究。文献[11]通过用户出行所需电量与实际电量计算得到出行满意值，从而进行充放电调控，但是未考虑到车主参与调控的意愿。已有研究主要考虑的是常规负荷及EV响应的随机性或不确定性，未考虑电动汽车多响应模式选择的消费意愿场景。文献[12]通过基本负荷以及可中断负荷描述了电网侧激励对用户侧响应参与率的影响，证明了电网侧存在针对用户参与率的最优激励政策。目前常用消费者心理学模型分析需求侧响应的不确定性，但是仅考虑了常规用户用电的不确定性[13]，或者EV用户充放电不确定性响应曲线[14]，或者利用条件风险价值自动响应符合用户心理的策略[15]。文献[16]引入价格弹性系数描述了电动汽车响应分时电价充电的不确定性；文献[17]通过二项分布描述车主充电习惯的不确定性，分析了不确定充电习惯对电动汽车充电负荷调节的影响；文献[18]考虑到用户到达、离开时间以及初始荷电状态的随机性，采用MCMC算法建立了概率模型；文献[19]引入用户响应系数来描述用户响应意愿对负荷分布的影响。与上述文献描述的不确定性不同，本文考虑的车主意愿模糊性是指无法准确预测车主选择不同模式需求响应的概率，是一种“似是而非”的不明确判断。

博弈理论已广泛应用于含EV微电网优化调度的建模之中，文献[20-21]表明基于博弈论的思想建立规划调度模型可以考虑多方的利益，实现共赢，是一种行之有效的方法。

本文针对EV多模式需求响应特点及车主模糊意愿，基于模糊推理预测理论和博弈理论，提出了含EV微电网系统的优化调度策略，建立了微电网与电动汽车的主从博弈优化模型，提升“车-网”系统综合调度效益。本文主要创新性工作及解决的关键问题包括以下几个方面。

1) 构建考虑多模式需求响应及车主意愿的EV车主侧优化模型。建立了EV车主的3种典型的多模式需求响应模型，满足车主的多模式需求响应诉求；基于模糊推理预测理论，综合主客观因素的影响，建立了车主的多模式选择决策模型，解决车主意愿的随机模糊性问题；在此基础上，建立了车主侧用能成本最小模型，提升了EV用能效益。

2) 在微电网侧，针对EV侧的多模式需求响应及车主意愿诉求特点，考虑微电网新能源完全消纳，针对净负荷曲线制定多模式动态电价激励政策，引导车主进行合理的模式选择，促进EV有序充放电；建立微电网净负荷曲线波动均方差最小和用能成本最小优化模型，实现微电网系统多目标优化。

3) 构建了微电网和EV车主的主从博弈模型。以微电网为主体，制定多模式动态电价策略，引导EV有序充放电，实现净负荷曲线波动均方差最小和运行成本最小；以EV车主为从体，制定车主多模式模糊决策模型，响应多模式动态电价，实现EV用能成本最小。经过主从模型的迭代优化，获得微电网侧最优多模式动态电价和电动汽车优化充放电策略集。

4) 采用非支配排序遗传算法求出微电网主体侧多目标优化模型的Pareto 前沿面，再利用模糊隶属度函数筛选最优折中解。通过仿真算例，分析验证了所提优化策略的有效性。

1 基于多模式电价激励和车主响应模糊意愿的含EV微电网博弈优化调度策略

针对规模化EV参与微电网调度的需求响应模式多样化，以及参与程度受车主选择意愿等因素影响，建立了考虑车主意愿的多模式动态分时电价激励政策，提出了基于多模式动态电价激励的含电动汽车微电网主从博弈优化调度策略，以期提升“车-网”系统的综合调度效益。

当EV接入时，考虑到EV充放电行为的随机性、无序性会加剧微电网负荷曲线的波动性。此时，微电网实施调峰调度，考虑EV侧的需求响应，通过制定合理的激励政策，引导EV有序充放电，达到“削峰填谷”的效果，促进“车-网”系统的安全高效运行。

1.1 考虑车主意愿的多模式动态分时电价激励政策

根据车主在微电网充电站的停留时间以及自身意愿分为即充即走(模式一)和参与调度两大类，其中参与调度又分为仅参加充电调度(模式二)和参与充放电调度(模式三)两类。

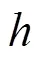
对于微电网的调峰调度来说，模式一、模式二和模式三的调峰效果依次增加。微电网最希望EV参与模式三的调度，其次是模式二。选择模式一的EV需要在短时间内大量充电，大量车主选择模式一不利于微电网的调峰调度，也是微电网最不希望的模式。为此，依据这3种响应模式和微电网净负荷曲线波动性的削峰填谷调度需求，在微电网侧制定多模式动态分时电价激励政策，如下所述。

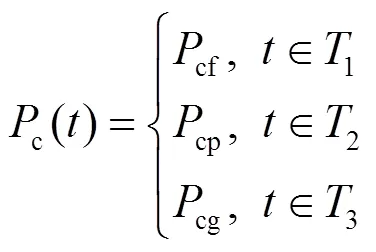
不同模式、不同时段下的充放电电价会影响车主成本，从而影响不同性格车主的最终选择。

1.2 含电动汽车微电网优化调度策略

微电网优先消纳新能源为负荷提供电能，剩余的负荷为净负荷，依据净负荷的波动特点，微电网实施调峰调度，制定多模式电价激励政策，引导EV有序充放电，达到削峰填谷的效果；EV车主响应微电网多模式电价激励政策，基于模糊推理决策模型选择响应模式，实现用能成本最小。微电网优先消纳新能源并考虑了EV需求响应之后，若新能源还有富余时将多余新能源存储于储能系统，不够时由储能系统放电支撑，还不够时则由柴油机组出力平衡。

图1为考虑EV多模式需求响应的含电动汽车微电网优化调度策略主体流程图。

图1 含EV的微电网优化调度策略

不同性格的车主考虑到自身利益，响应微电网侧电价激励，根据停留时间选择成本较小的模式进行充电，微电网为了促进车主参与充放电调度，会适当提高模式一的电价系数，降低模式二和模式三的电价系数，但是考虑到微电网自身的成本，电价系数也不宜太高或者太低，需要通过博弈模型优化，达到“车-网”共赢。

1.3 车-网主从博弈优化调度策略

微电网主体侧以多模式动态电价为决策变量，实现净负荷曲线波动均方差最小和运行成本最小；EV车主从体侧以EV充放电策略为决策变量，实现EV用能成本最小。双方的决策相互影响，经过主从博弈模型的迭代优化，获得微电网侧最优多模式动态电价和电动汽车优化充放电策略集。实施日前调度，以24 h为一个调度周期，每15 min(0.25 h)为一个调度窗口，将全天划分为96个调度时段。

2 考虑多模式电价激励和车主响应模糊意愿的含EV微电网主从博弈优化调度模型

考虑微电网和电动汽车属于不同的利益主体，均具有自我趋利属性。基于博弈理论，建立主从博弈优化模型，获得微电网侧最优多模式动态电价策略和电动汽车优化充放电策略。

2.1 博弈主体侧目标函数

微电网作为博弈主体领导者率先做出决策制定电价，引导电动汽车的充放电行为，起到削峰填谷的作用，其目标函数分别为运行成本最小和负荷均方差最小。

1) 微电网运行成本目标函数

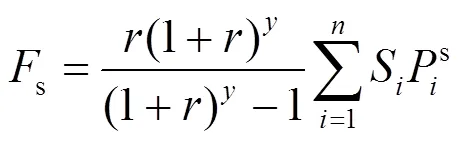
2) 微电网负荷均方差目标函数

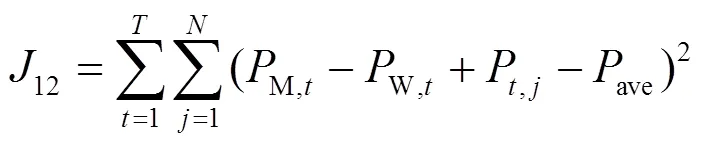
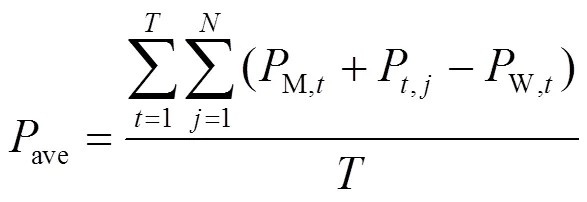
2.2 博弈从体目标函数

2.2.1车主信息

根据2009年美国交通部对私人电动汽车的调查结果[22]，车主进入充电站开始充电时刻和离开充电站时刻均近似满足正态分布。电动汽车到达充电站和离开充电站的时间关系有两种：一种是到达和离开均在一天之内完成，另一种是到达充电站在前一天，离开时间在第二天，具体停车时间如图2所示。本文将在优化建模中，据此构建EV停车时间段信息模型。

图2 停车时间段

2.2.2博弈从体车主目标函数

1) 模式一目标函数

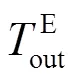
车主在停留时间段内通过快充充电，车主成本由电池损耗费用和根据模式一电价得到的充电费用构成。

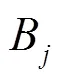
2) 模式二目标函数

选择模式二的车主将参与充电调度。考虑到多次充放电带来的电池损耗，车主不愿意参加放电调度，这类车主将在达到期望荷电状态后在期望时间离开充电站。

(1) 慢充模式下的车主成本

车主通过慢充达到期望电量，车主成本由根据模式二电价得到的充电费用和电池损耗费用构成。

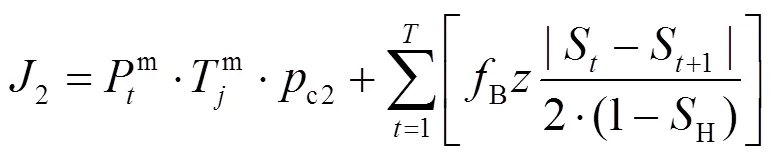
(2) 快充模式下车主成本

车主通过快充达到期望电量，车主成本由根据模式二电价得到的充电费用和电池损耗费用构成。

3) 模式三目标函数

选择模式三的车主将参与充、放电调度。车主根据停留时间选择快充或慢充，若停留时间段小于慢充时间段，选择快充，反之选择慢充。车主通过不同充电方式达到期望电量，车主成本由根据模式三电价得到的充电费用、放电补偿和电池损耗费用构成。

2.3 车主决策模型

由于影响车主充放电模式决策的因素具有模糊不确定性，基于模糊逻辑[23]建模，根据车主性格的差异性以及不同模式下的充电成本，模糊推理得到该用户最有可能选择的充放电模式，具体流程如图3所示。

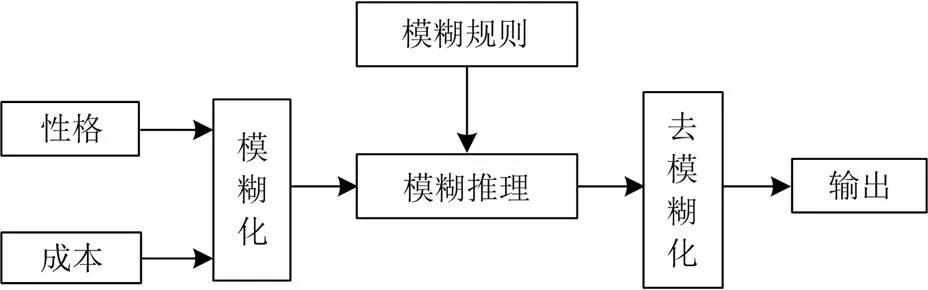
图3 基于模糊逻辑的用户决策模型结构

表1 模糊子集与成本关系对应表

本文设定了18条模糊控制规则如表2所示。根据模糊逻辑规则表和Mamdani推理法则[25]，得到模糊控制器的输出特性曲面，如图7所示。

图7描述了不同性格车主在对比3种模式下的车主成本之后得到的最终决策，输出值越接近于1，表示该车主选择模式三的概率越大，输出值越接近于0，表示该车主选择模式一的概率越大。

图4 性格隶属度函数

图5 成本隶属度函数

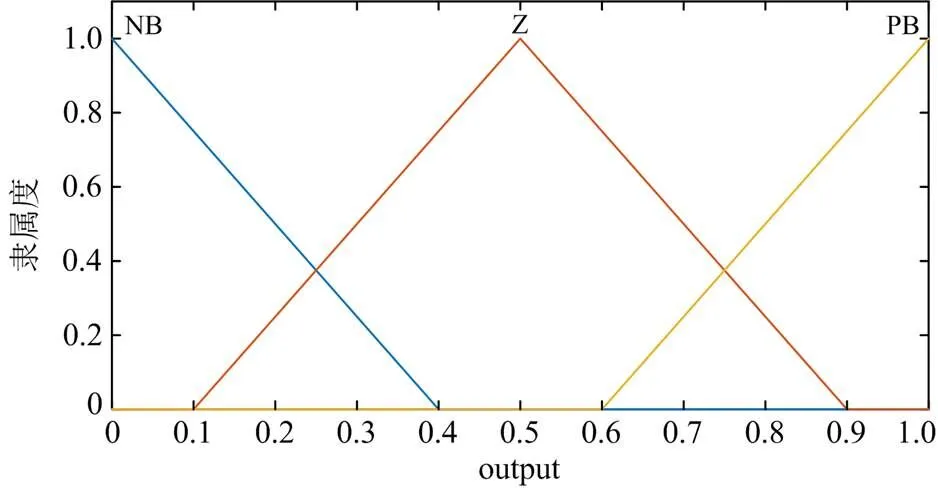
图6 输出隶属度函数

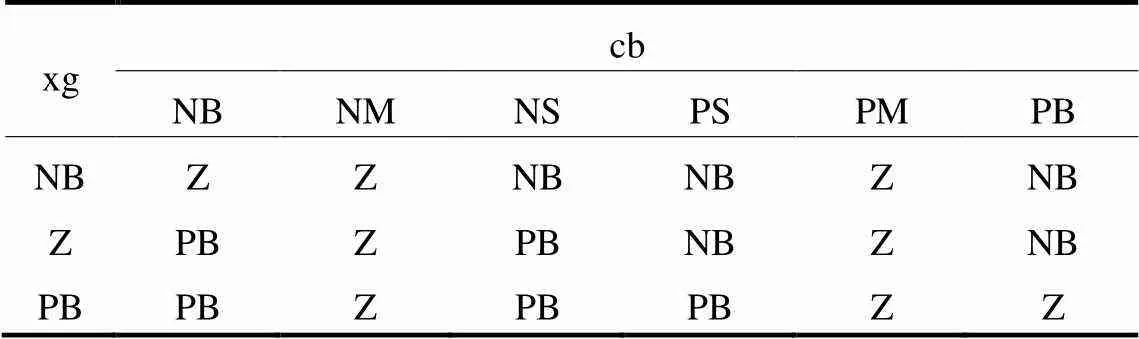
表2 模糊控制规则表

图7 模糊逻辑控制器输出特性曲面

2.4 约束条件

1) 时间约束

车主参与充放电调度的总时长不超过停留时长，且充放电不能同时进行。

2) 电动汽车充放电功率约束

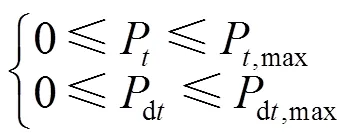
3) 电动汽车荷电状态约束

4) 柴油机、风电出力极限约束

3 优化模型求解

具体求解过程分为3个步骤进行。

2) 基于车主意愿决策模型得到车主的充放电模式，再计算EV在不同模式不同时段下的充放电功率。具体计算流程如图8所示。

选择模式一的车主采用步骤1)的方法计算不同时段充放电功率。

选择模式三的车辆既充电又放电，根据停留时间选择快充和慢充模式。考虑到车辆入网时间、入网时荷电状态以及不同时段电价大小的不确定性，为了在短时间内寻求最优充放电策略使每辆EV都能在高电价时间段放电，低电价时间段充电，采用粒子群算法进行循环迭代得到车主成本最小的充放电策略。具体流程如图10所示。

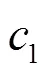
图8 EV充放电功率计算流程

图9 停车时间段

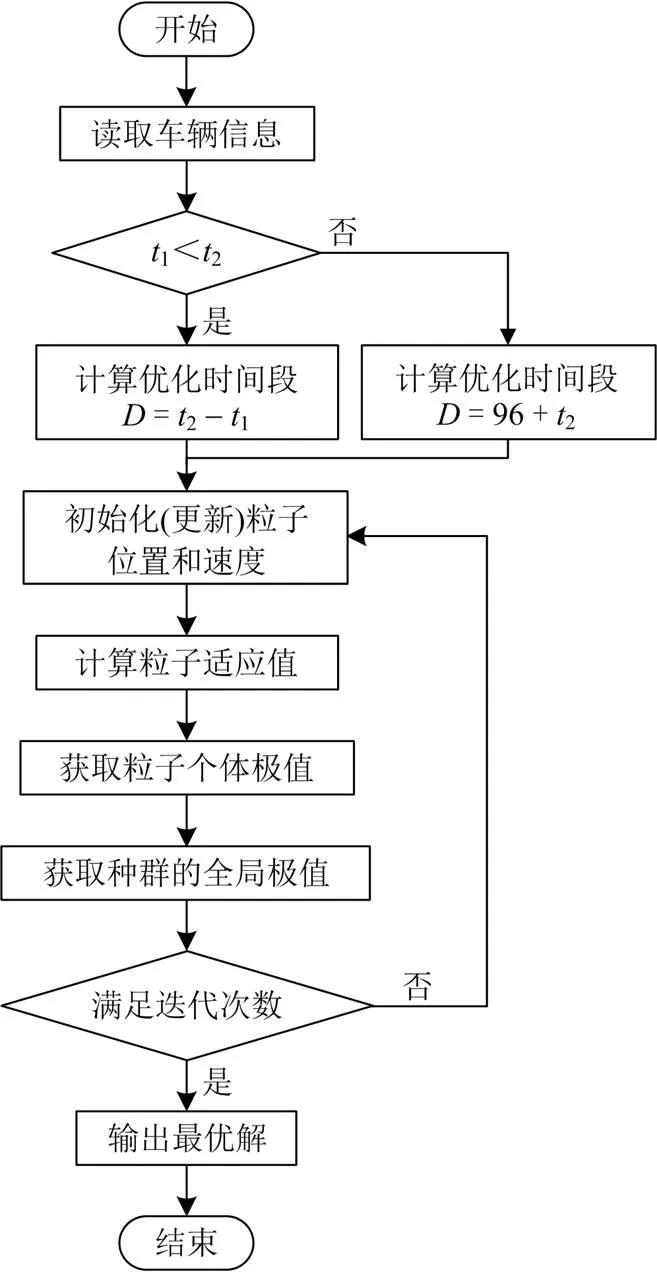
图10 模式三EV充放电功率计算流程

该博弈模型达到均衡需要满足：

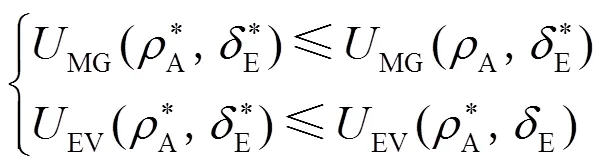
4 算例分析

4.1 参数设置

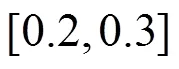
图11 主从博弈模型求解流程

表3 分时电价初始值

图12为EV入网前微电网的净负荷曲线，可以看出，微电网原始负荷在中午和晚上都存在负荷高峰，消纳全部风电后，微电网净负荷曲线峰时段集中在中午，谷时段集中在凌晨，激励电动汽车有序在峰时段放电谷时段充电，达到削峰填谷的目的。

4.2 不同激励政策对优化结果的影响

为了对比分析不同激励政策下的EV响应效果，设置4种典型案例。

案例一：无激励政策下的无序充电场景，即不考虑微电网电价的激励作用以及车主性格的差异性，EV入网立即充电。

图12 EV入网前微电网净负荷曲线

案例二：单一模式分时电价激励下的EV有序充放电场景，即考虑传统分时电价激励，EV在电价激励下有序进行充放电过程。

案例三：考虑车主模糊意愿的单一模式分时电价激励下的EV有序充放电场景，即在案例二传统电价激励的基础上考虑了不同性格车主参与调度的不确定性。

案例四(本文方法)：考虑多模式动态电价激励和车主模糊意愿的有序充放电场景，即在案例三的基础上，针对车主参与调度意愿的差异性设置了不同模式电价，EV在多模式动态电价激励下有序充放电过程。

图13为4种案例下的EV充(放)电对微电网净负荷曲线的调节效果对比图。图中：蓝线描述了EV无序入网充电时的净负荷曲线，12：00—15：00 时段以及16：00—17：00时段处于峰时段，00：00—07：00时段处于谷时段，与表3的时段划分基本吻合；红线描述了在传统分时电价激励下的净负荷曲线，相比于无序充电峰谷差明显减小，12：00—15：00 时段内的负荷尖峰明显降低，00：00—07：00时段内的负荷低谷明显升高；绿线描述了考虑车主意愿和传统分时电价激励的净负荷曲线，与案例二相比，曲线波动明显更剧烈，在12：25时产生的负荷尖峰甚至超过了案例一的蓝线，红线和绿线分别代表了传统分时电价激励下的理想情况与实际情况，在工程实际中通过传统分时电价激励得不到理想的调度效果；黑线描述了采用本文所提策略得到的EV有序充放电后的净负荷曲线，黑线不仅比绿线更平滑，而且与红线的波动状态基本相同，同时在12：25时的尖峰也略低于红线，说明本文提出的模型在真实反映工程实际的基础上，确实能有效引导EV由高峰充电低谷放电到高峰放电低谷充电，达到削峰填谷的目的。

图13 EV不同充电策略的微电网净负荷曲线比较图

图14展示了案例四中微电网主体侧多目标寻优的Pareto前沿面以及最优折中解的筛选情况，根据最优折中解来确定微电网运行成本和微电网净负荷均方差的最小值，不同充电策略下的具体数值如表4所示。

图14 案例四的Pareto前沿面

EV在不同充电策略下车主成本、微电网成本以及净负荷均方差数值如表4所示。可以发现，相比于案例一，案例四的车主成本和净负荷均方差都明显下降。案例四的车主成本相较于案例二略有增加，是因为传统分时电价没有考虑到有车主不愿参加调度的情况，本文策略中针对不愿意参与调度的EV采用高价充电；但是相比于案例三，车主成本又有所下降，这是车主可以在停留时间段内选择价格更低的时段进行充电。

表4 不同充电策略下的具体优化结果

针对案例四优化后的3种模式下充放电系数如图15所示。以09：00(即第36时段)为例，此时3种模式的电价系数分别为1.41、0.83和0.58，可得模式一电价为1.96元/kWh，即峰时段电价与电价系数乘积。由表3可知，此时处于平时段，则模式二和模式三电价分别为0.69、0.48元/kWh，即平时段电价与电价系数乘积，体现了3种模式下电价大小的设计策略。

图15 3种模式下的充放电系数

4.3 多模式响应对优化结果的影响

在4.2节的基础上，分析仅考虑单模式响应时，是否存在与期望偏差过大或达不到最佳调度效果的情况，分析根据车主意愿以及实际情况建立的多模式响应的调度策略是否可以达到最好的调度效果。其净负荷曲线结果如图16所示，其成本及净负荷均方差结果如表5所示。

图16 响应模式对净负荷曲线调节效果的影响

表5 响应模式对车网成本及净负荷均方差的影响

由图16和表5可以发现，当车主全部选择模式一时所得到的净负荷均方差最大，此时的调度效果最差，这是因为所有车主入网立即充电，没有考虑微电网负荷曲线波动情况；当车主全部选择模式三时，虽然峰谷差较全选模式一有所下降，但是曲线波动太频繁，会影响微电网运行稳定性，且此模式下车主成本较其他模式高出太多；当车主全部选择模式二时的净负荷曲线与多模式响应时的净负荷曲线最接近，但是相比于多模式响应微电网成本略高，同时在工程实际中要考虑有车主不愿意参与调度的情况，因此车主根据自身意愿进行多模式响应得到的优化结果是最好的。

4.4 车主意愿对优化结果的影响

在4.3节的基础上，进一步分析实施多模式电价激励下，是否考虑车主模糊意愿对调度结果的影响。其净负荷曲线结果如图17所示，其成本及净负荷均方差结果如表6所示。

图17 车主意愿对净负荷曲线调节效果的影响

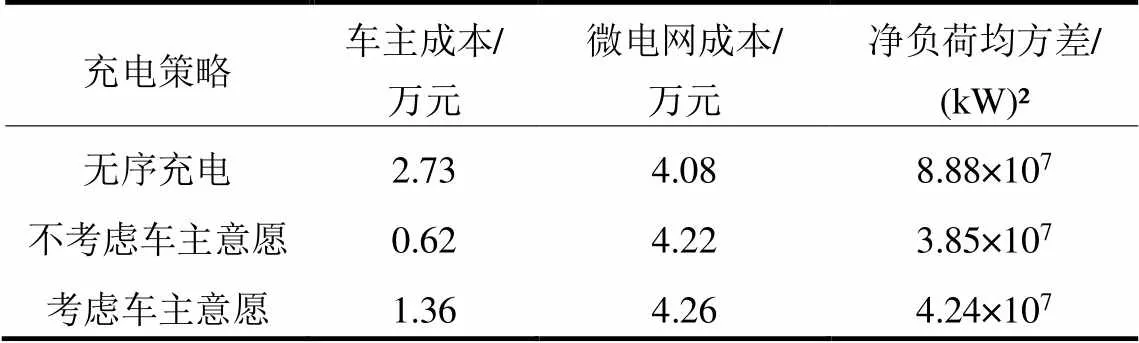
表6 车主意愿对车网成本及净负荷均方差的影响

分析图17和表6结果可知，在保持多模式电价数值一致的情况下，不考虑车主意愿的净负荷方差更小，净负荷曲线效果更好，车主成本更低，但前提是车主能够按照微电网设计的模式参与响应；当考虑车主模糊意愿时，车主成本和微电网成本增加，净负荷均方差变大，净负荷曲线效果变坏，净负荷曲线不仅频繁波动而且在12：00时增大了负荷尖峰，说明车主并未按照微电网主体设计好的模式及其电价系数进行响应，导致响应效果的恶化。因此，建立电动汽车调度模型时，在考虑多响应模式的情况下，进一步考虑车主对多模式的选择意愿联合优化激励电价是必要的，可以更贴合EV响应模式的多样性和模糊性这一实际工程场景。

4.5 EV规模对优化结果的影响

目前EV的规模不断扩大，为了验证本文提出的策略在未来大规模EV入网的工程实际中的可行性，选择EV数量分别为500、800、1000和1200参与调度，净负荷曲线如图18所示，车主平均成本、微电网成本和净负荷的均方差如表7所示。

图18 不同EV数量优化对比曲线

表7 EV规模对优化结果影响具体数值

分析图18和表7的结果可以发现，随着EV数量增多，车主平均成本变化不大，00：00—12：00时段内的填谷效果更加明显，同时整体的净负荷均方差不断减小，说明随着EV数量日益增多，本文提出的调度策略削峰填谷效果越好。

5 结论

随着EV用户消费需求的提升，EV参与电网调度的需求响应模式呈现差异性和多样性，参与意愿具有模糊性。本文提出的基于车主模糊意愿得到的多模式动态电价策略在完全消纳新能源的前提下，将EV用户需求响应分为3种典型模式，根据不同模式下的电价策略，激励用户参与充放电调度。基于对比算例可得到如下结论：

1) 为适应EV需求响应模式的多样性和参与响应意愿的模糊性，本文提出的车-网互动策略在含EV微电网日前调度中能明显降低负荷曲线峰谷差，减少车主成本，提高微电网运行效益。

2) 微电网侧实施基于车主意愿的动态电价激励政策，不仅促进了新能源的消纳，还有利于提高电动汽车车主参与调度的积极性。车主侧响应多模式动态电价，在贴合工程实际的基础上降低微电网成本和净负荷均方差，减小曲线波动，增强微电网运行稳定性。针对EV侧的多模式需求响应可为实际工程应用提供参考。

3) 考虑车主意愿时的车主成本相比于不考虑车主意愿时更高，反映了车主的决策意愿未必一定会选择微电网主体所期望的模式，因此，建立电动汽车调度模型时考虑车主意愿更贴合工程实际。

[1] 赵玉, 徐天奇, 李琰, 等. 基于分时电价的电动汽车调度策略研究[J]. 电力系统保护与控制, 2020, 48(11): 92-101.

ZHAO Yu, XU Tianqi, LI Yan, et al. Research on electric vehicle scheduling strategy based on time-shared electricity price[J]. Power System Protection and Control, 2020, 48(11): 92-101.

[2] 姚颖蓓, 陆建忠, 傅业盛, 等. 华东地区电动汽车发展趋势及用电需求预测[J]. 电力系统保护与控制, 2021, 49(4): 141-145.

YAO Yingbei, LU Jianzhong, FU Yesheng, et al. Electric vehicle development trends and electricity demand forecast in East China[J]. Power System Protection and Control,2021, 49(4): 141-145.

[3] 杨国清, 罗航, 王德意, 等. 分时电价与电动汽车优化调度的主从博弈模型[J]. 电力系统及其自动化学报, 2018, 30(10): 55-60.

YANG Guoqing, LUO Hang, WANG Deyi, et al. Leader- follower game model of time-of-use electricity price and optimized plug-in electric vehicle dispatching[J]. Proceedings of the CSU-EPSA, 2018, 30(10): 55-60.

[4] 李正烁, 郭庆来, 孙宏斌, 等. 计及电动汽车充电预测的实时充电优化方法[J]. 电力系统自动化, 2014, 38(9): 61-68.

LI Zhengshuo, GUO Qinglai, SUN Hongbin, et al. Real- time charging optimization method considering vehicle charging prediction[J]. Automation of Electric Power Systems, 2014, 38(9): 61-68.

[5] 赵兴勇, 王帅, 吴新华, 等. 含分布式电源和电动汽车的微电网协调控制策略[J]. 电网技术, 2016, 40(12): 3732-3740.

ZHAO Xingyong, WANG Shuai, WU Xinhua, et al. Coordinated control strategy research of microgrid including distributed generations and electric vehicles[J]. Power System Technology, 2016, 40(12): 3732-3740.

[6] 姚伟锋, 赵俊华, 文福拴, 等. 基于双层优化的电动汽车充放电调度策略[J]. 电力系统自动化, 2012, 36(11): 30-37.

YAO Weifeng, ZHAO Junhua, WEN Fushuan, et al. A charging and discharging dispatching strategy for electric vehicles based on bi-level optimization[J]. Automation of Electric Power Systems, 2012, 36(11): 30-37.

[7] 张西竹, 刘洵源, 杨文涛, 等. 动态分时电价机制下的电动汽车分层调度策略[J]. 电力建设, 2018, 39(12): 73-80.

ZHANG Xizhu, LIU Xunyuan, YANG Wentao, et al. A hierarchical scheduling strategy for electric vehicles under dynamic time-of-use tariff mechanism[J]. Electric Power Construction, 2018, 39(12): 73-80.

[8] 吴宛潞, 韩帅, 孙乐平, 等. 负荷聚合商多类型需求侧资源激励价格制定一般模型及应用[J]. 电力建设, 2021, 42(1): 1-9.

WU Wanlu, HAN Shuai, SUN Leping, et al. A general incentive pricing model and its application for multi-type demand-side resources of load aggregators[J]. Electric Power Construction, 2021, 42(1): 1-9.

[9] 胡鹏, 艾欣, 张朔, 等. 基于需求响应的分时电价主从博弈建模与仿真研究[J]. 电网技术, 2020, 44(2): 585-592.

HU Peng, AI Xin, ZHANG Shuo, et al. Modelling and simulation study of TOU Stackelberg game based on demand response[J]. Power System Technology, 2020, 44(2): 585-592.

[10] 程杉, 陈梓铭, 徐康仪, 等. 基于合作博弈与动态分时电价的电动汽车有序充放电方法[J]. 电力系统保护与控制, 2020, 48(21): 15-21.

CHENG Shan, CHEN Ziming, XU Kangyi, et al. An orderly charging and discharging method for electric vehicles based on a cooperative game and dynamic time-of-use price[J]. Power System Protection and Control, 2020, 48(21): 15-21.

[11] 杨春萍, 赵祺, 祁兵, 等. 基于用户利益与出行意愿的电动汽车充放电调度策略[J]. 电测与仪表, 2018, 55(8): 106-112.

YANG Chunping, ZHAO Qi, QI Bing, et al. Charge and discharge scheduling strategy of electric vehicle based on interest and travel intention of users[J]. Electrical Measurement & Instrumentation, 2018, 55(8): 106-112.

[12] 彭文昊, 陆俊, 冯勇军, 等. 计及用户参与不确定性的需求响应策略优化方法[J]. 电网技术, 2018, 42(5): 1588-1594.

PENG Wenhao, LU Jun, FENG Yongjun, et al. A demand response strategy optimization considering user participation uncertainty[J]. Power System Technology, 2018, 42(5): 1588-1594.

[13] 王蓓蓓, 孙宇军, 李扬. 不确定性需求响应建模在电力积分激励决策中的应用[J]. 电力系统自动化, 2015, 39(10): 93-99, 150.

WANG Beibei, SUN Yujun, LI Yang. Application of uncertain demand response modeling in Power-score incentive decision[J]. Automation of Electric Power Systems, 2015, 39(10): 93-99, 150.

[14] 朱兰, 刘伸, 唐陇军, 等. 充放电不确定性响应建模与电动汽车代理商日前调度策略[J]. 电网技术, 2018, 42(10): 3305-3317.

ZHU Lan, LIU Shen, TANG Longjun, et al. Modeling of charging and discharging uncertainty and research on day-ahead dispatching strategy of electric vehicle agents[J]. Power System Technology, 2018, 42(10): 3305-3317.

[15] 杨晓东, 张有兵, 赵波, 等. 供需两侧协同优化的电动汽车充放电自动需求响应方法[J]. 中国电机工程学报, 2017, 37(1): 120-130.

YANG Xiaodong, ZHANG Youbing, ZHAO Bo, et al. Automated demand response method for electric vehicles charging and discharging to achieve supply-demand coordinated optimization[J]. Proceedings of the CSEE, 2017, 37(1): 120-130.

[16] 杨健维, 苟方杰, 黄宇, 等. 基于不确定性测度的居民小区电动汽车充电分时电价制定策略[J]. 电网技术, 2018, 42(1): 96-102.

YANG Jianwei, GOU Fangjie, HUANG Yu, et al. Residential area electric vehicle charging pricing strategy based on uncertainty measure[J]. Power System Technology, 2018, 42(1): 96-102.

[17] 杨冰, 王丽芳, 廖承林, 等. 不确定充电习惯对电动汽车充电负荷需求及充电负荷调节的影响[J]. 电工技术学报, 2015, 30(4): 226-232.

YANG Bing, WANG Lifang, LIAO Chenglin, et al. Effects of uncertainty charging habits on electric vehicles’ charging load demand and the charging load regulation[J]. Transactions of China Electrotechnical Society, 2015, 30(4): 226-232.

[18] 孙韩, 陈宗海, 武骥. 计及电动汽车不确定性的家庭微电网实时能量调度策略[J]. 电网技术, 2019, 43(7): 2544-2551.

SUN Han, CHEN Zonghai, WU Ji. Online energy dispatch strategy for residential microgrid considering uncertainty of electric vehicle[J]. Power System Technology, 2019, 43(7): 2544-2551.

[19] 王毅, 麻秀, 万毅, 等. 基于分时充放电裕度的电动汽车有序充放电引导策略[J]. 电网技术, 2019, 43(12): 4353-4361.

WANG Yi, MA Xiu, WAN Yi, et al. Sequential charge- discharge guidance strategy for electric vehicles based on time-sharing charging-discharging margin[J]. Power System Technology, 2019, 43(12): 4353-4361.

[20] 李咸善, 马凯琳, 程杉. 含多区域综合能源系统的主动配电网双层博弈优化调度策略[J]. 电力系统保护与控制, 2022, 50(1): 8-22.

LI Xianshan, MA Kailin, CHENG Shan. Dispatching strategy of an active distribution network with multiple regional integrated energy systems based on two-level game optimization[J]. Power System Protection and Control, 2022, 50(1): 8-22.

[21] 王瑞, 程杉, 汪业乔, 等. 基于多主体主从博弈的区域综合能源系统低碳经济优化调度[J]. 电力系统保护与控制, 2022, 50(5): 12-21.

WANG Rui, CHENG Shan, WANG Yeqiao, et al. Stackelberg game optimization method for microgrid cluster considering electricity price mechanism[J]. Power System Protection and Control, 2022, 50(5): 12-21.

[22] 田立亭, 史双龙, 贾卓. 电动汽车充电功率需求的统计学建模方法[J]. 电网技术, 2010, 34(11): 126-130.

TIAN Liting, SHI Shuanglong, JIA Zhuo. A statistical model for charging power demand of electric vehicles[J]. Power System Technology, 2010, 34(11): 126-130.

[23] 郭宴秀, 苏建军, 马临超, 等. 基于IT2FLC的HESS太阳能充电站功率分配策略[J]. 智慧电力, 2022, 50(5): 62-68, 76.

GUO Yanxiu, SU Jianjun, MA Linchao, et al. Power Allocation strategy of hybrid energy storage solar charging station based on IT2FLC[J]. Smart Power, 2022, 50(5): 62-68, 76.

[24] 聂琳真, 管家意, 卢炽华, 等. 基于模糊逻辑的高速公路微观换道行为[J]. 北京工业大学学报, 2018, 44(3): 424-432.

NIE Linzhen, GUAN Jiayi, LU Chihua, et al. Freeway lane changing behavior based on fuzzy logic[J]. Journal of Beijing University of Technology, 2018, 44(3): 424-432.

[25] SHAKEEL F M, MALIK O P. Fuzzy based energy management system for a micro-grid with a V2G parking lot[C] // 2020 IEEE Electric Power and Energy Conference (EPEC), November 9-10, 2020, Edmonton, AB, Canada: 1-5.

[26] 李咸善, 解仕杰, 方子健, 等. 多微电网共享储能的优化配置及其成本分摊[J]. 电力自动化设备, 2021, 41(10): 44-51.

LI Xianshan, XIE Shijie, FANG Zijian, et al. Optimal configuration of shared energy storage for multi-microgrid and its cost allocation[J]. Electric Power Automation Equipment, 2021, 41(10): 44-51.

[27] 陆立民, 褚国伟, 张涛, 等. 基于改进多目标粒子群算法的微电网储能优化配置[J]. 电力系统保护与控制, 2020, 48(15): 116-124.

LU Limin, CHU Guowei, ZHANG Tao, et al. Optimal configuration of energy storage in a microgrid based on improved multi-objective particle swarm optimization[J]. Power System Protection and Control, 2020, 48(15): 116-124.

Optimal dispatch strategy considering fuzzy intention of multi-mode demand response of vehicle owners

LI Xianshan1, 2, ZHOU Xiaolan1, 2, YAO Junwei3, XIE Qiongyao3

(1. Hubei Provincial Key Laboratory for Operation and Control of Cascaded Hydropower Station (China Three Gorges University), Yichang 443002, China; 2. College of Electrical Engineering & New Energy, China Three Gorges University,Yichang 443002, China; 3.State Grid Yichang Power Supply Company, Yichang 443002, China)

The demand response of modern electric vehicle (EV) users is characterized by diversity and fuzziness of willingness. When a single incentive policy is implemented, the EV response will not achieve the desired effect. Therefore, this paper proposes a master-slave game optimization scheduling strategy for an EV microgrid considering the multi-mode demand response and fuzzy intention of vehicle owners. The main body of the microgrid formulates a multi-mode dynamic electricity price incentive policy for net load, guides the EV to make choices in multi-mode electricity price, and promotes orderly charging and discharging of EV. It also realizes minimum net load mean square deviation and operational cost. Based on the fuzzy logic reasoning willingness decision, the vehicle owner responds to the multi-mode dynamic electricity price to minimize the vehicle owner cost. The NSGA-II algorithm is used to analyse the optimization model to obtain the optimal multi-mode dynamic electricity price and EV charging and discharging strategy. Simulation results verify the effectiveness of the proposed method.

master-slave game;EV owner's willingness; multi-mode response; dynamic electricity price

10.19783/j.cnki.pspc.220697

国家自然科学基金项目资助(51607105)；湖北省技术创新重大项目资助(2017AAA132)

This work is supported by the National Natural Science Foundation of China (No. 51607105).

2022-05-11；

2022-09-05

李咸善(1964—)，男，博士，教授，博士生导师，研究方向为微电网运行与控制、电力系统运行与控制、水电站仿真与控制；E-mail: lixianshan@ctgu.edu.cn

周晓岚(1998—)，女，硕士研究生，研究方向为电力系统运行与控制、微电网优化调度。E-mail: 952978228@qq.com

(编辑 姜新丽)