江尖水利枢纽工程闸门加固结构的静、动力场影响变化研究

李 玲，吴宇婧

（无锡市水利工程管理中心,江苏 无锡 214000）

1 引言

闸门乃是水利枢纽工程中重要控水、调水的水利设施[1-2],其安全稳定性对水利枢纽工程的运营可靠性密切相关,故开展闸门结构的安全稳定性分析很有必要。研究水工建筑稳定性不仅仅只针对静力场[3-4],且应考虑结构地震动作用下响应特征,综合评价水工结构安全可靠。李傲赢[5]、李静等[6]采用振动台试验方法,开展了结构地震动破坏试验研究,探讨地震动荷载作用下结构破坏过程及破坏机理,为抗震设计提供了试验依据。张文皎等[7]、崔晓玉等[8]为优化结构体型设计,采用模型试验方法,对溢洪道、消能池等水工设施开展了渗流场特征分析,对有利于结构渗流安全的设计方案开展了综合评判,丰富了工程优化设计的评判成果。张杨杨[9]、李忠彦[10]采用仿真计算手段,对水闸、挡墙等结构开展了应力、位移计算,分析了不同设计方案下静力场特征影响变化,从而提供了工程优化设计的依据。本文基于江尖水利枢纽工程节制闸门的加固支撑钢结构设计优化,探讨从静、动力场多维度下评价结构设计的最优性,而不仅仅依赖于一个维度的评判,对工程的设计及运行优化均有参考价值。

2 工程设计分析

2.1 工程概况

江尖水利枢纽工程是无锡城市防洪枢纽工程重要控制设施,该枢纽承担着防洪、排涝、蓄水调度的水利功能,该工程按照200年一遇洪水标准设计,堤内最高水位设计为25.5 m,可作为太湖生态补水的重要地表水源。江尖水利枢纽沿南、北走向建设干堤工程,总长度超过50 km,地表径流水系长度超过60 km,全枢纽工程配备有60 m3/s 的提水泵站及调水节制闸工程。根据对江尖水利枢纽工程调查得知,该泵站所采用的电动机组,如图1所示,排水流量为最大设计值的75%～85%,输水耗散率不超过25%,泵站输水渠道采用采用防渗混凝土作为衬砌材料,且渠底配置有防渗垫层,厚度约为0.4 m；另为有效管理该泵站,建设有集监测、数据采集、实时控制及信息管理储存一体式的泵站管理系统,能够有效对泵站机电设备、动能机组及水闸启闭装置进行控制,有效确保水利设施运行安全性。江尖枢纽工程另一重要水工建筑为多孔式节制闸,通流面为三孔设计,总净宽75 m,设计最大流量为125 m3/s,闸内、外设计水位分别为9.86 m、9.65 m,其闸上、下水位与蓄水库容及上游泄流量关系曲线见图2[11-12]。

图1 泵站电动机机组

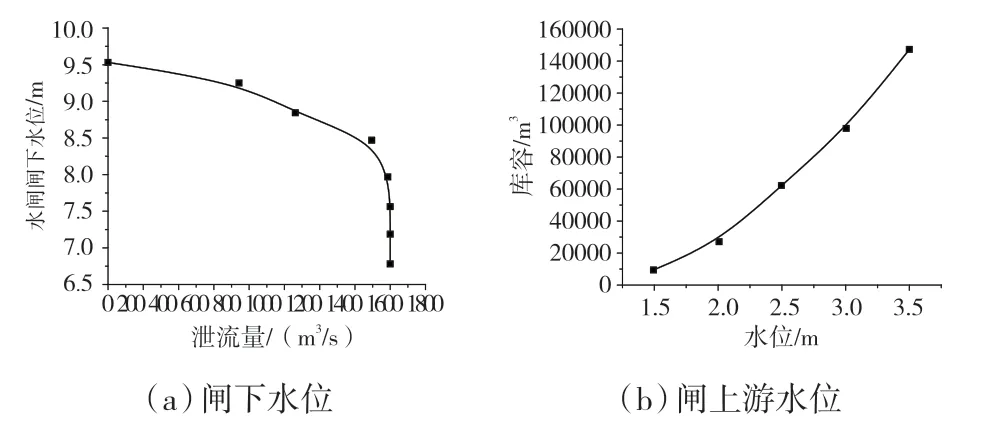
图2 水闸水位变化关系

江尖节制闸采用液压启闭机作为闸门启闭系统,闸室底板厚度为1 m,采用预应力混凝土作为闸墩结构,厚度为1.6 m,根据水文监测表明,闸墩周围流场稳定性较佳,设计水位运营下闸室内流速稳定在1.2 m/s,最大波幅不超过25%。为减少水力冲刷势能对下游闸身影响,采用混凝土预制挡墙结构设立在下游2.5 m 处,墙厚为1.6 m,墙高度达3.5 m,进、出水段分别设置浆砌石护坦,厚度均为0.45 m。另消能池建设在顺水流向,轴长度为6.5 m,进、出水口采用防渗土工格栅为护底材料,厚度为0.35 m,两侧配置有翼墙结构,箱涵厚度为1.2 m,墙顶、底板厚度分别为0.8 m、0.6 m。根据对江尖水利枢纽调查得知,目前泵站与多孔节制闸均面临老化危险,受运营年限与设计参数限制,目前水利枢纽水资源调度率下降45%,泵站部分齿面出现锈蚀、滚道磨损严重等,节制闸闸门支撑结构受限,挡水及排沙率下降,面板上钢结构急需加固。对此,讨论先期对节制闸门支撑加固结构进行维修设计,是对提升江尖水利枢纽运行效率可行性的研究。

2.2 设计模拟

根据对支撑加固钢结构分析,目前江尖节制闸多孔闸门支撑钢结构剖面见图3,全轴长度为6 m,上、下翼缘厚度分别为60 mm、45 mm,主要构件材料为型钢,截面肋板厚度为40 mm,腹板厚度为35 mm,加劲肋间距为3.6 m,支撑结构与闸门的接触面上增设有预制垫板,其轴心位于支撑结构剖面跨中处,减少应力集中对支撑结构的损害。本文根据对该支撑结构截面分析,在翼缘设计参数及加劲肋参数均已优化确定的前提下,探讨对腹板设计参数优化,特别是针对型钢截面腹板倾角开展对比分析。

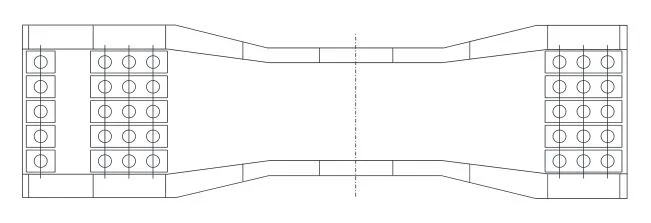
图3 多孔闸门支撑钢结构

利用COMSOL Multiphysical 建立数值仿真计算模型[13],见图4。该模型中包括节制闸整体模型与钢结构模型,其中整体模型单元划分网格后共有335682 个,节点数268758 个,本构体为弹性模型,满足主要材料强度变形要求。该钢梁结构计算模型中顶、底面分别设定为法向单一约束与全向约束边界条件,计算闸上、下水位按照运行期设定。模型中X～Z 正向分别取闸室右岸方向、下游消能池向及结构重心上方。

图4 计算模型

本文从钢梁结构腹板与水平面夹角入手,由于腹板夹角的选取与取材密切相关,过大的腹板夹角需要较长的腹板,对腹板的长厚比控制不利,一般设定腹板夹角不超过90°,且腹板长度不低于肋板长度,故夹角不应低于60°,在加固钢结构其他设计参数均保持一致的前提下,上、下翼缘宽度均为2.2 m,宽厚比为30,腹板高度为3 m,设定腹板夹角位于70°～90°,按照梯次3°的对比方案设定,分别为70°（A 方案）、73°（B 方案）、76°（C 方案）、79°（D 方案）、82°（E方案）、85°（F 方案）、85°（G 方案）,典型钢结构腹板剖面见图5。采用Taft 地震波作为地震动力特性研究工况外荷载,采用拟静力法计算钢结构地震动响应特征。基于上述七种腹板夹角方案开展静、动力对比计算分析,评价设计方案的综合优势。

图5 结构型钢截面剖面

3 设计参数与结构静力特征关系

3.1 应力特征

根据对不同设计方案下开展静力场计算,获得腹板夹角参数与结构拉应力关系,见图6。从图中可知,截面上各处拉应力随腹板夹角参数变化具有差异性,下翼缘与肋板处拉应力与腹板夹角参数为负相关,当腹板夹角愈大,两处拉应力在各方案中均为递减,但降幅逐渐减小,特别是在夹角82°后处于稳定状态。在腹板夹角参数70°方案内,下翼缘处拉应力为8.4MPa,而夹角76°、82°、88°方案内拉应力较前者分别减少了37.8%、55.1%、55.8%；从整体上随方案变化可计算出,腹板夹角每增大3°,则下翼缘处拉应力平均降幅为12.3%,全过程中最大降幅位于70°～73°方案,而在夹角低于82°方案内,其平均降幅为18.3%,而在夹角82°～88°方案内的平均降幅仅为0.8%。同样的,肋板处拉应力亦是如此,其在全方案内平均降幅为14.1%,而在低于82°方案内的平均降幅为20.4%,超过82°方案时最大降幅与平均降幅分别仅为2.4%、1.5%。从此两处拉应力量值影响变化来看,应尽量控制腹板夹角在82°时才更突出设计“性价比”[14-15]。

图6 拉应力与腹板夹角参数关系

上翼缘处拉应力在全方案内呈先减后增变化,其变化节点为夹角82°方案,该方案下拉应力为2.05 MPa,夹角超过该方案后,上翼缘处拉应力甚至超过了肋板、下翼缘拉应力,其在夹角85°、88°方案内拉应力较之夹角82°下分别增长了42.1%、115.9%,而在腹板夹角低于82°方案区间内,平均降幅为22.5%。腹板拉应力影响变化特征与上翼缘处有所类似,但其在夹角低于82°方案内处于较稳定状态,约为1.89 MPa,而夹角85°、88°方案下拉应力较之前一稳定阶段内分别增长了23.5%、69.2%。因而,从上翼缘与腹板拉应力的影响特征来看,腹板夹角超过82°时,不利于结构设计安全。

从应力量值影响变化分析得知腹板夹角82°时较为有利,故本文提取获得了该方案下截面各处大主应力分布特征,见图7。观察该方案下大主应力分布可知,上翼缘处大主应力分布具有对称态势,以左跨主应力集中效应更显著；下翼缘中跨中主应力超过两端部,但大主应力最大值位于端部,整体水平以跨中更集中,此主要与预制垫板的接触面所在位置有关；腹板上最大主应力为0.97 MPa,满足安全设计要求,腹板间主应力分布具有相似性；肋板的最大主应力位于截面中部,达1.82 MPa,两边部主应力分布量值较小,以肋板中部受力更显著。整体上看,该方案下大主应力分布较合理,量值满足结构强度要求[16]。

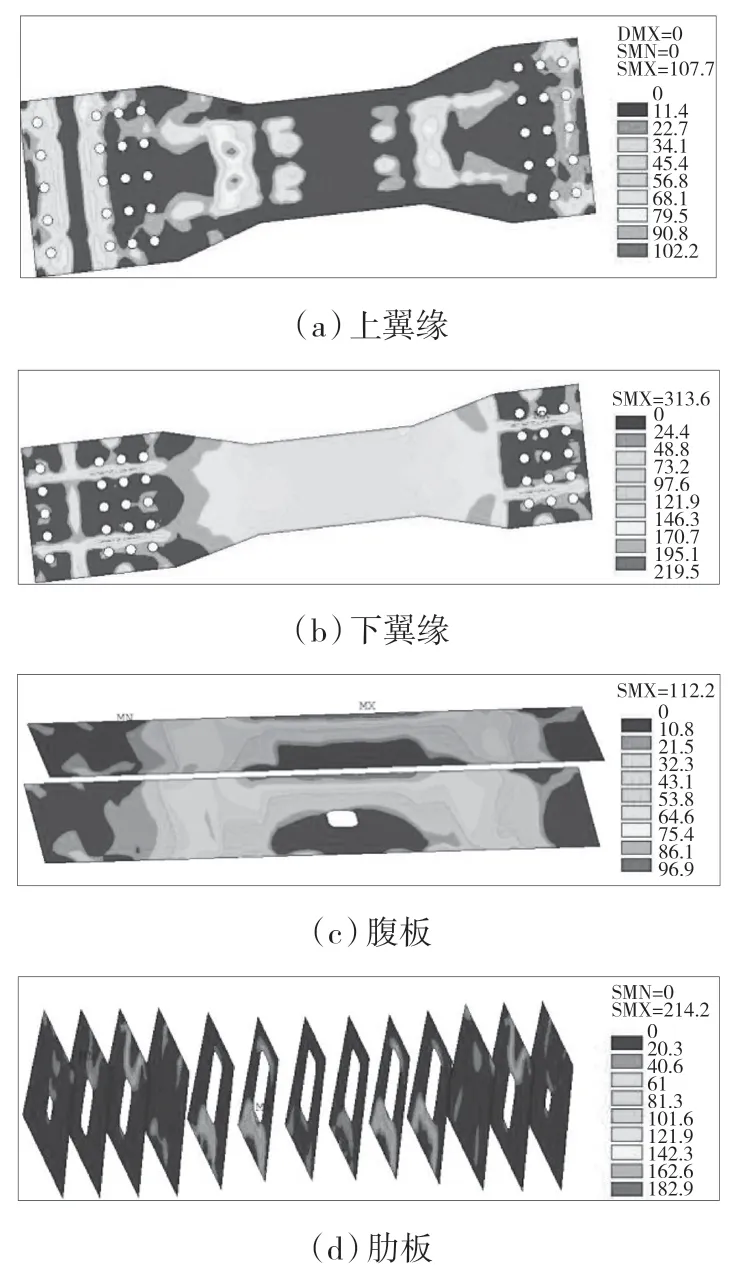
图7 大主应力分布特征

3.2 位移特征

根据对支撑结构的位移计算,获得各向位移、截面挠度与腹板夹角参数变化关系,见图8。从图中可知,三向位移随腹板夹角均为先减后增变化,在夹角82°下为各向位移最低,X～Z 向在该方案下分别为8.21 mm、5.62 mm、9.41 mm,当腹板夹角低于82°时,各向位移均为递减,X～Z 三向在该区间方案内平均降幅为16.9%、20.1%、23.5%,而夹角超过82°后,其位移与腹板夹角参数为正相关关系,表明腹板夹角过大,不利于控制支撑结构位移,各向位移的平均增幅达36.7%、38.3%、39.4%。从结构变形控制角度考量,应避免腹板夹角超出位移抑制区间方案,即夹角应低于82°。

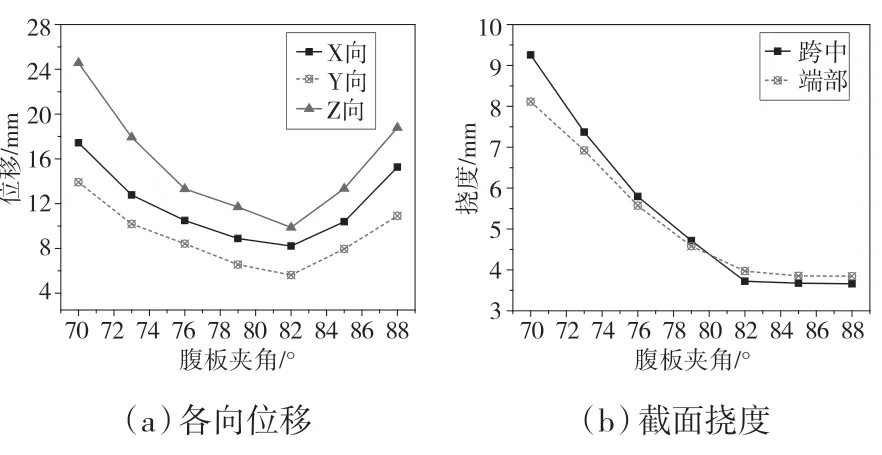
图8 结构变形特征

比较截面跨中与端部处挠度可知,两者挠度随腹板夹角参数均为递减变化,在腹板夹角70°下跨中挠度为9.26 mm,而夹角为76°、82°、88°时挠度较之前者分别减少了37.4%、59.8%、60.1%,降幅主要集中在夹角82°前方案内,而在此方案之后,跨中挠度降幅较小。当夹角在70°～82°时,跨中挠度最大降幅达21.4%,为76°～79°方案,而平均降幅也达20.3%,在该方案之外,其平均降幅仅为0.9%,且其挠度在夹角79°方案后演变成低于端部挠度。端部挠度与跨中处有所类似,在腹板夹角70°～82°与超过82°时,分别具有平均降幅16.3%、1.6%。由此可知,综合挠度与位移的分析评判,腹板夹角82°方案下位移控制效果最佳,较为有利结构刚度设计。

4 设计参数与结构动力响应特征关系

在Taft 地震波不同峰值反应谱工况的叠加下[17],计算获得加固支撑结构地震动力响应特征,本文以结构加速度响应值为分析对象,见图9。

图9 加速度响应特征

从图中可看出,地震波反应谱峰值加速度愈大,则结构地震动响应值愈高,如在Taft 地震波40 cm/s2下腹板夹角76°方案内加速度响应值为174.2 mm/s2,而地震波反应谱峰值参数每增长40 cm/s2时,则结构加速度响应值平均可增长1.02 倍；当夹角为85°、88°方案时,则加速度响应值随地震波峰值参数变化的平均增幅分别为73.9%、55.9%,表明夹角愈大,结构动力响应值受地震波频率参数影响敏感度更弱。另一方面,当地震波荷载参数一致时,在腹板夹角递增过程中,结构加速度响应值均为递增,但增幅在夹角超过82°时显著增大,在地震波40 cm/s2下腹板夹角为76°～82°时,在夹角方案每梯次增长过程中,平均增幅为19.1%,而整体方案中平均增幅为52.7%,较大的增幅集中在夹角方案82°～88°内,该方案内的平均增幅可达120%。当地震波荷载加速度参数为80 cm/s2、120 cm/s2时,其加速度响应值的平均增幅分别为40.4%、31.8%,但两者工况中腹板夹角82°前梯次方案内的增幅均低于超过82°的区间方案。从抗震设计方面考虑,应避免结构受过大的地震动响应,当腹板夹角低于82°时抗震可靠性更大。

5 结论

（1）下翼缘与肋板拉应力与腹板夹角参数为负相关关系,但降幅逐渐减小,在夹角超过82°后降幅分别仅为0.8%、1.5%；上翼缘处拉应力在夹角82°方案下拉应力最低,而腹板拉应力在低于夹角82°方案时稳定在1.89 MPa,两者在夹角超过82°方案后均为递增；夹角82°方案下结构截面大主应力分布合理,无较大区域拉应力集中。

（2）三向位移随腹板夹角均为先减后增变化,以夹角82°方案下位移最低,分别为8.21 mm、5.62 mm、9.41 mm；截面跨中与端部处挠度随腹板夹角参数均为递减,但降幅也减小,特别是在夹角82°方案后,跨中挠度甚至低于端部处。

（3）地震波荷载参数与结构加速度响应值为正相关关系,且腹板夹角参数愈小,动力响应值更为敏感；腹板夹角递增,结构加速度响应值也增大,但增幅在夹角82°后方案更为显著。

（4）综合对比结构静、动力响应特征,腹板夹角82°方案下设计最佳。