基于FRFT的单基地MIMO雷达稳健波束形成算法

吕 岩, 曹 菲, 许剑锋, 冯晓伟

(1. 火箭军工程大学核工程学院, 陕西 西安 710025; 2. 中国人民解放军96746部队, 新疆 库尔勒市 841000)

0 引 言

线性调频(linear frequency modulation, LFM)[1-2]信号具有容易实现和对多普勒频移不敏感等特点,近年来在雷达、声呐和信息通信系统中得到了较为广泛的应用[3-6]。分数阶傅里叶变换(fractional Fourier transform, FRFT)[7-8]可以视为一种时频平面上的旋转算子,通过合理设置算子的变换阶次或旋转角度,能够对LFM信号实现良好的能量集中。此外,FRFT还具备其他优良的特性,例如自成像、连续性、线性、旋转加法和比例特性等[9-10]。

目前,大量文献对基于FRFT的自适应波束形成算法开展了研究。文献[11]针对雷达或声呐应用中信号回波信噪比(signal to noise ratio, SNR)较低且噪声为色噪声的情况,提出了一种基于FRFT的分数阶数值选择的自适应波束形成算法。该方法能够最大限度地提高LFM信号的分数阶谱峰度,将期望的LFM信号能量集中在最佳时频域,但在SNR较高时性能将受到限制。文献[12]针对FRFT在变SNR和多目标时的波束形成性能展开研究,仿真实验的结果表明,FRFT较其他算法在计算效率、精度和分辨率方面具备一定的优势。文献[13]将FRFT和四阶累积量相结合用于宽带信号波束形成,通过主动声呐仿真实验验证了算法的性能。综上可知,FRFT被广泛应用于自适应波束形成算法中,但现有文献尚未对算法在阵列信号模型存在多种失配条件下的稳健性进行研究验证[14-15]。

为了提升自适应波束形成算法的稳健性,基于对角加载和最差情况性能优化[16-19]等方法被相继提出,有效提升了波束形成算法在期望信号(signal of interest,SOI)导向矢量误差和快拍数较低时的稳健性,但上述方法无法有效消除SOI分量对波束形成算法性能的影响。为了达到这一目的,诸多学者在协方差矩阵重构方面也做了大量的研究工作[20-22],有效解决了SNR较高时的SOI自消现象。

本文以单基地多输入多输出(multiple input multiple output, MIMO)雷达系统为研究对象,针对LFM形式的正交频分复用(orthogonal frequency division multiplexing, OFDM)信号,提出了一种新的稳健自适应波束形成算法。算法首先对匹配滤波后的雷达回波信号进行FRFT,得到峰值点,作为阵列的观测数据。而后,利用观测值构建接收信号的协方差矩阵,并使用Capon谱估计方法重构干扰加噪声协方差矩阵。通过求解优化问题估计实际导向矢量,最终得到阵列的最优权值。

1 信号模型

如图1所示,考虑一个由均匀线阵组成的收发共址单基地MIMO雷达系统,假设发射天线阵元数为Q,接收阵元数为N。

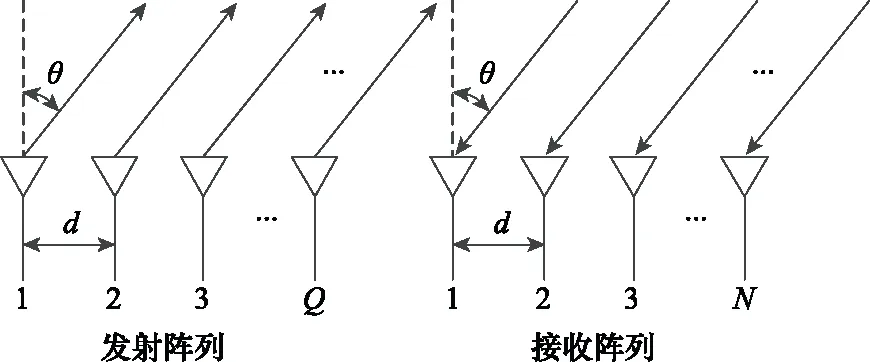
图1 MIMO雷达阵列结构Fig.1 Structure of MIMO radar array

在发射端,发射天线阵列的Q个阵元发射相互正交的信号,本文针对LFM-OFDM信号开展研究,则第q个阵元的发射信号[23-24]可表示为

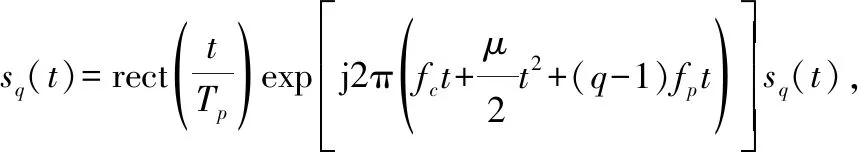
(1)

式中:rect(·)为矩形窗函数;Tp为脉冲宽度;fc为发射信号载频;μ=B/Tp为线性调频信号的调频斜率;B为频偏;fp=1/Tp为阵元间的频率步进量;sq(t)为第q个阵元的发射波形。

假设存在1个远场SOI和L-1个干扰,分别以波达方向(direction of arrival, DOA)θl到达阵列,则第n个接收阵元收到的回波信号rn(t,τk)可表示为

(2)

式中:σl表示第l个目标或干扰的散射系数;τk=2r(tk)/c表示回波的时间延迟，tk表示慢时间，r(tk)为目标或干扰与雷达的距离，c为电磁波速;fd为多普勒频移;wn(t)为高斯复噪声;aq(θl)和bn(θl)分别为

aq(θl)=exp(j2π(q-1)dtrasinθl/λ)

(3)

bn(θl)=exp(j2π(n-1)drecsinθl/λ)

(4)

式中:λ=c/(fc+(B+(Q-1)fp)/2)为信号最短波长,为避免出现栅瓣或空间模糊,发射和接收阵元间距设置为dtra=drec=λ/2。

由于各阵元发射的信号相互正交,分别对每个接收阵元的接收回波信号进行匹配滤波,可将各接收信号分离,得到:

j2π(q-1)fpτk+j2πfdt)aq(θl)bn(θl)}+wn(t)

(5)

式中:rq,n(t,τk)为第q个阵元的发射信号经第n个阵元接收后的匹配滤波输出。

2 基于FRFT的波束形成算法

2.1 FRFT

FRFT可以视为一种时频域的旋转变换,可以建立时域和频域之间的联系。假设存在信号f(t),则其FRFT变换可以表达为

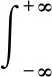
(6)

式中:Fp和Xα表示FRFT算子;α代表旋转角度;p为FRFT的分数阶数;Kα(t,u)表示变换的核函数:

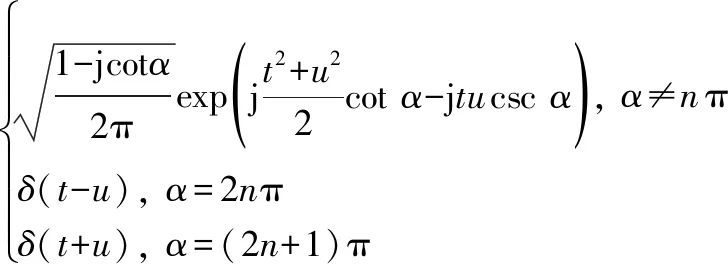
(7)

典型的线性调频信号可以表示为

(8)

式中:κ为调频斜率。则h(t)的FRFT[25]为

(9)

当旋转角α=α0=-arctan(1/κ)时,h(t)的FRFT将会形成峰值,可以表述如下:

(10)

式中:Tc是脉冲重复周期。当式(10)中u=0时,可得到最大值为

(11)

时移函数h1(t)=h(t-τ0)(τ0表示时移)的FRFT可以表述为

(12)

频移函数h2(t)=h(t)exp(j2πf0t)(f0表示频移)的FRFT为

(13)

2.2 本文信号模型的FRFT

为便于分析,选取式(5)中与第l个目标相关的输出进行讨论,定义A为包含σl的目标幅度衰减因子,因此可得

rq,n,l(t,τk)=Aexp(-j2πfcτk+jπμ(t-τk)2-
j2π(q-1)fpτk+j2πfdt)aq(θl)bn(θl)+wn(t)

(14)

对式(14)进行FRFT,可得

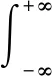
(15)

Rq,n,l=Bl(τk)F2(α0,-fd,u)F1(α0,τk,u-fdsinα0)·
Xα0(h)(u-τkcosα0-fdsinα0)

(16)

其中,

Bl(τk)=Aexp(-j2π(fc+(q-1)fp)τk)

(17)

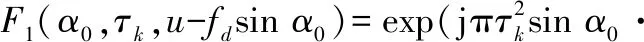
(18)

(19)

根据式(16),当u=τkcosα0+fdsinα0时,可得最大值为

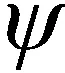
(20)

合并式(20),进一步可得出:

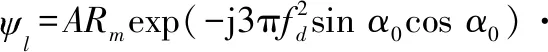
(21)

整理式(21)后可得

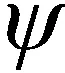
(22)

其中,

(23)

φ1=(fc+(n-1)fp+fdcos2α0)

(24)

(25)

根据式(22)～式(25),由于fc远大于(n-1)fp、fdcos2α0和φ2,因此可得到峰值的估计为

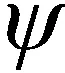
(26)

根据式(14)和式(26),可以得到:

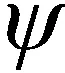
(27)

式中:c(θl)=aq(θl)bn(θl),Wn(τk,fd)表示噪声wn(t)的FRFT。

假定为达到预期的欺骗干扰效果,干扰所产生回波信号的调频斜率与目标信号相同,则可得

(28)

式中:Rq,n,σ(τk,fd)为干扰信号经FRFT后的输出表达式。

2.3 稳健波束形成算法

对MIMO雷达匹配滤波后的每一组信号进行FRFT,由于目标和干扰回波信号的调频斜率相同,因此在相同的FRFT阶次下,目标和干扰回波信号都可以形成峰值。选择分数域上的峰值点作为该阵元的观测值,则可得到矩阵:

Xe=[x1,e,x2,e,…,xV,e]T

(29)

式中:xv,e=[x1,x2,…,xM]代表M个较大的峰值点组成的矢量,v=1,2,…,V为匹配滤波后的信号数量,V=Q×N,e=1,2,…,E表示回波数量,因此可得

X=[X1,X2,…,XE]

(30)

根据式(30),构造接收信号的协方差矩阵为

(31)

使用Capon谱估计方法[27],可得

(32)

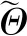
(33)

重构协方差矩阵后,可以通过求解优化问题估计实际导向矢量:

(34)

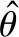
(35)

3 仿真分析

仿真基于收发共址的MIMO雷达,发射阵元数Q=6,接收阵元数N=8。为验证所提算法的性能,将本文提出的算法与文献[19-22]中的算法相对比。对于所有的算法,SOI的扇形区域设置为Θ=[θ1-5°,θ1+5°],所得的仿真结果均为200次蒙特卡罗[29-30]实验后的平均值,除实验2外,其余仿真实验回波数均设置为6,其余雷达相关的仿真参数如表1所示。

表1 雷达仿真参数

仿真中的模拟回波信号由SOI、干扰信号和噪声组成,其中干扰信号的调频斜率和SOI相同,目标和干扰信号相关的仿真参数设置如表2所示,其中INR表示干噪比(interference to noise ratio)。图2为雷达回波经FRFT后的三维图,根据图2可知,经FRFT后回波信号主要形成了3个峰值,分别为一个SOI加两个干扰信号。

表2 信号仿真参数

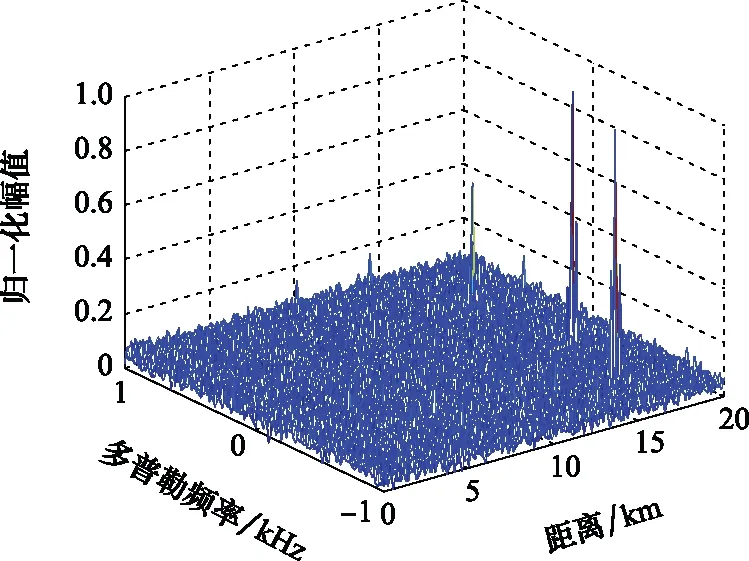
图2 回波信号FRFT结果Fig.2 Result of echo signal after FRFT

图3和图4分别为信干噪比(signal to interferece plus noise ratio, SINR)随SNR的变化曲线和SINR随回波数的变化关系,由于信号模型为针对LFM-OFDM信号采样回波的FRFT变换,所以仿真中的快拍数量被模拟回波的数量取代,使其更接近于真实应用场景。根据图3可知,文献[19]算法在SNR较高时性能严重下降,文献[21-22]算法性能均低于文献[20],本文所提算法的输出SINR在不同SNR处均高于其他算法。值得引起注意的是,本文所提算法在SNR较高时性能曲线接近最优值。根据图4可得出,在回波数量小于3时,本文所提算法性能和文献[19]及文献[22]相近,输出SINR较文献[20]低。当回波数大于4时,本文算法性能大幅提升,输出SINR迅速提高至最优值附近并高于其他算法,原因可能为当回波数量较少时,由峰值点组成的FRFT域协方差矩阵维数低,影响算法性能。

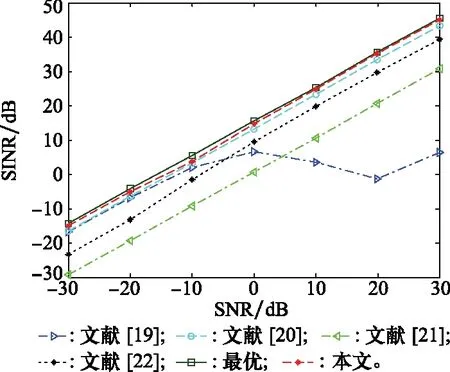
图3 SINR随输入SNR的变化曲线Fig.3 Variation curve of SINR with input SNR

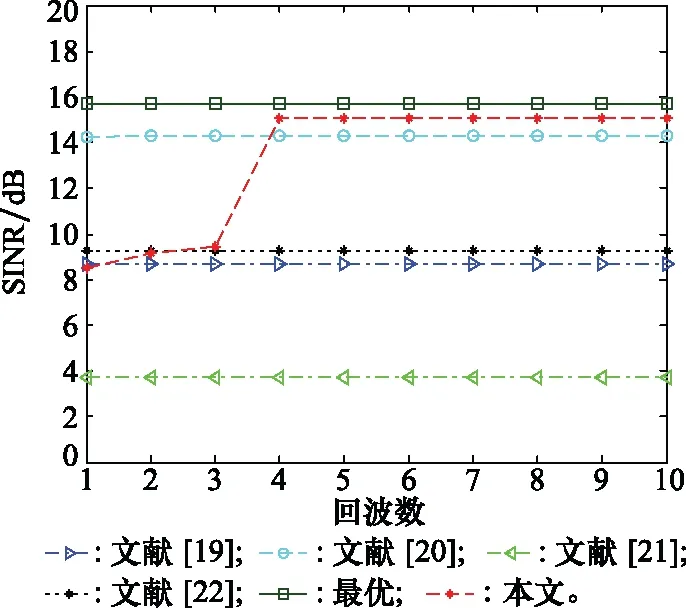
图4 SINR随回波数变化趋势Fig.4 Trend of SINR with the number of echose

实验 1主要检验所提算法在信号源的速度和距离不同于表2 时的性能,仿真参数设置如表3所示。图5和图6分别为雷达回波经FRFT后的三维图和输出SINR随SNR的变化趋势。

表3 实验1仿真参数

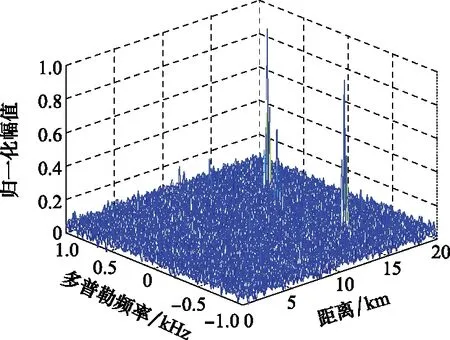
图5 回波信号经FRFT的三维图Fig.5 Three-dimensional diagram of echo signal after FRFT

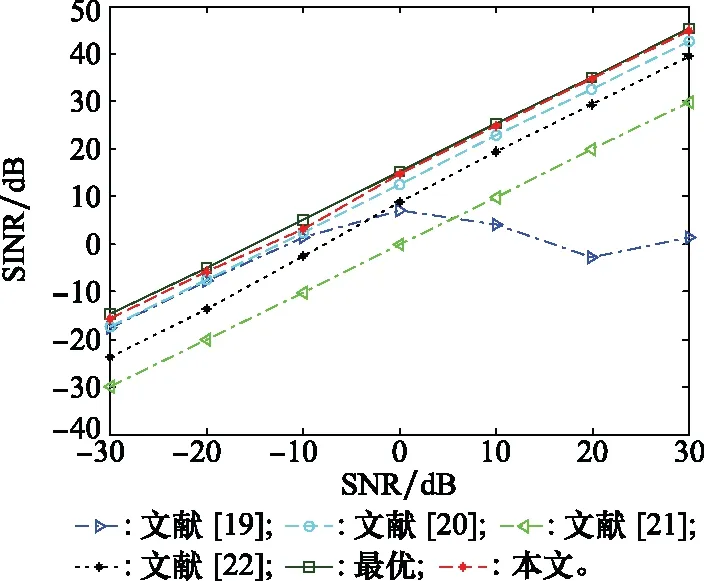
图6 不同算法SINR的变化趋势Fig.6 Trends of SINRs of different algorithms

根据图5可知,信号源的距离和速度变化后,经FRFT变换,回波信号同样主要形成了3个峰值,分别为一个SOI和两个干扰信号。从图6可以看出,本文所提算法的输出SINR在不同SNR处仍高于其他算法,且在SNR较高时比其他算法更加接近最优SINR。

实验 2主要检验所提算法在SNR不同时,输出SINR随回波数的变化关系,将SNR设置为20 dB进行仿真。图7为SINR随回波数的变化趋势,根据图7可知,回波数量小于2时,本文所提算法性能和文献[22]相近,高于文献[19]和文献[21]。当回波数大于3时,本文算法输出SINR高于其他算法。

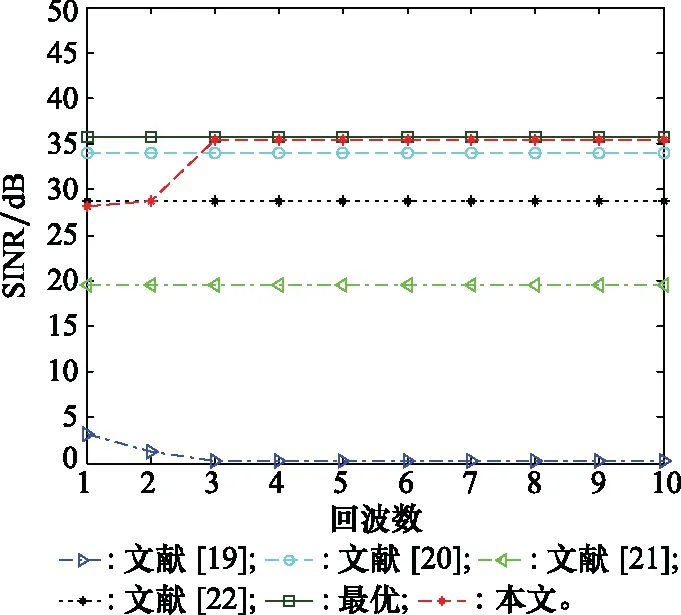
图7 实验2中不同算法的输出结果Fig.7 Output results of different algorithms in experiment 2

实验 3主要检验所提算法在期望信号DOA失配情况下的性能,假设目标的估计DOA随机分布在[θ1-4°,θ1+4°]范围内,θ1代表SOI的DOA真实值,保持不变。图8为SINR随SNR的变化趋势曲线,根据图8可知,SNR较低时,文献[19]和文献[20]算法优于本文算法,随SNR逐渐提高,本文算法输出SINR得到提升,尤其在高SNR情况下,性能优于其他算法。

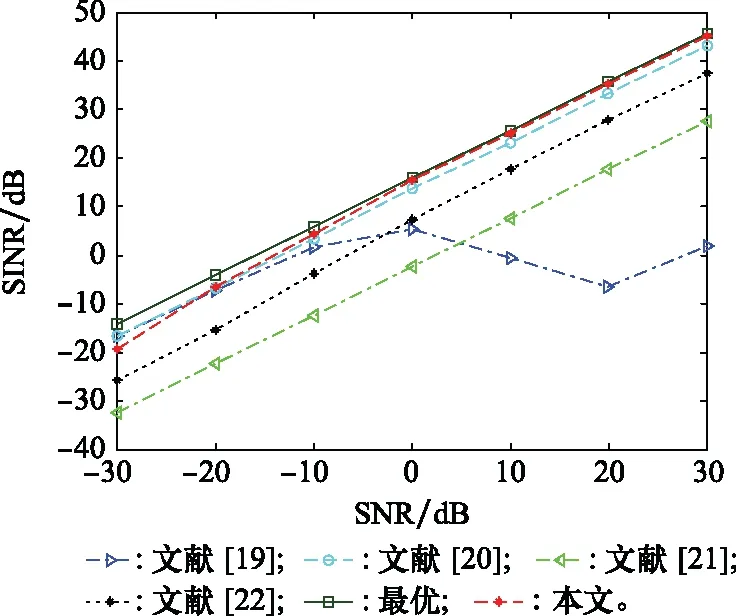
图8 DOA随机误差下输出SINR和SNR的对比Fig.8 Output SINR versus SNR in DOA radom error

实验 4主要检验非相干局部散射对波束形成器输出SINR性能的影响。假定SOI具有时变性的导向矢量,回波信号可以表示为

(36)

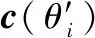
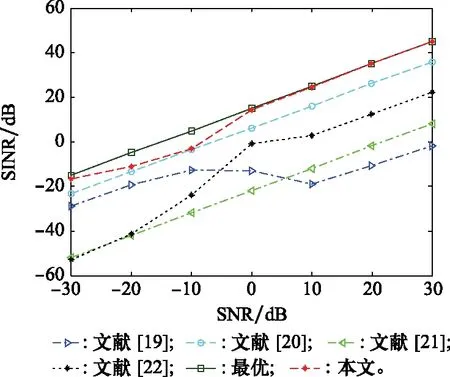
图9 非相干局部散射下输出SINR和SNR的对比Fig.9 Output SINR versus SNR in incoherent local scattering

实验 5主要检验所提算法在阵元位置存在误差情况下的性能,仿真中接收阵元位置随机分布在[(n-1)drec-0.05,(n-1)drec+0.05]范围内。图10为SINR随SNR的关系曲线,可以看出,各类算法的性能均受到阵元位置误差影响,在SNR较低时,文献[19]算法的输出SINR略高于其他算法。随着SNR逐渐提高,本文所提算法在高SNR时的优越性得到彰显,输出的SINR虽较最优值有所差距,但高于其他算法。

4 结 论

本文以单基地MIMO雷达系统为研究对象,针对LFM-OFDM信号,提出了一种新的稳健自适应波束形成算法。所提算法首先利用LFM信号的性质,对匹配滤波后的雷达回波信号进行FRFT,经推导并化简后得到较大的几个峰值点作为阵列的观测值。其次,利用观测值构建接收信号的协方差矩阵,并使用Capon谱估计方法重构干扰加噪声数据协方差矩阵。而后,通过求解优化问题估计实际导向矢量,从而得到阵列的最优权值。最后,通过计算机仿真实验,分别对比了目标和干扰信号速度和距离不同、目标信号DOA失配、非相干局部散射、阵元位置误差情况下,阵列输出SINR随SNR或回波数量的变化关系,对所提算法的性能进行了验证。