A high-safety active/passive hybrid control approach for compressor surge based on nonlinear model predictive control

Hanlin SHENG, Qian CHEN, Jie ZHANG, Tianhong ZHANG

Jiangsu Province Key Laboratory of Aerospace Power System, College of Energy and Power Engineering, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China

KEYWORDS Active control;Compressor surge;Flow estimator;Hybrid system;Model predictive control

Abstract Surge active control can expand the stable operating range of the compressor.However,the difficulty of flow measurement,dynamic uncertainty disturbance,actuator delay characteristics,hard constraints of control variable,and system security measures have not been fully considered in the existing active control system,which significantly hinders its engineering application.Therefore,a nonlinear model predictive surge active control method is first presented based on flow estimator designed by using a continuous-time Kalman filter for dealing with the hard constraint of control variable and the impact of actuator delay of compression system with dynamic uncertainty.Then,a high-safety active/surge passive hybrid control strategy is designed, dominated by the surge active control and supplemented by the surge passive control,to ensure the compression system’s safe and stable operation. Lastly, the simulation results suggest that the flow estimator accurately estimates the compressor flow.When considering the delay impact of the actuators and sensors and measurement noise on the system,the proposed method exhibits stronger robustness than the existing methods. The active/surge passive hybrid control strategy can successfully ensure the compression system’s safe and stable operation. This paper is of high practical significance for the engineering application of future compressor surge active control technologies.

1. Introduction

Surge and rotating stall are the two critical aerodynamic instability states of the compressor with serious impact on its operating state. These two states may lead to a performance degradation or even damage and destruction of the mechanical structure.1-3Accordingly, in the design of the conventional compressor control system, a sufficient surge margin is left to keep the operating point away from the surge line, so as to ensure that the compressor always runs safely in the stable area at the expense of high performance.With the rapid development of industrial technology, high-performance requirements (e.g., high-efficiency and high-pressure ratio) have been raised for the compression system such as turbomachinery in aero-engines and gas turbines.4,5Thus, to comprehensively study the compressor performance from the perspective of control, surge active control should be conducted to expand its operating range.6

Fig. 1 Surge active control strategy.

In 1986 Epstein,et al.7first proposed a surge active control strategy(see Fig.1)to solve the problem of compressor performance limitation due to surge and rotating stall,specifically,a feedback control device was adopted to make the compressor operate stably at a high-pressure ratio and high-efficiency point close to the surge line. Compared with the surge passive control strategy,the proposed strategy can expand the operating range of the compressor by 20%. Subsequently, Williams and Pinsley, et al.8,9investigated the stability expansion through the additional disturbance active control in a centrifugal compressor. Despite some positive results was illustrated,the control system was found to be complicated and inconvenient for engineering practice due to the requirement of twodimensional (2D) sensors and actuators. Abed and Wang,et al.10,11used classical nonlinear dynamics to propose a surge active control method based on bifurcation theory, which is simple and easy to implement. However, it can hardly determine the amplitude of disturbed flow in practice accurately.Considering the unknown characteristics of compressor components and based on the second-order Moore-Greitzer(MG) model with Close Coupled Valve (CCV), Sheng, et al.proposed robust adaptive sliding mode control of compressor surge by using backstepping method12and robust adaptive backstepping active control of compressor surge based on wavelet neural network,13respectively.As revealed by the simulation results, the above control methods can be used to expand the stable operating range of the compressor with steady-state control error of approximate 0%. However, they did not consider the constraint of the control variable, therefore, a negative phenomenon is identified. Therefore, Fu,et al.14studied the finite-time adaptive sliding mode control of compressor surge under uncertain characteristic in the presence of disturbance for the established MG model with CCV of centrifugal compressor.The simulation results showed that,compared with Ref. 12, although the constraint problem has been solved, it is difficult to deal with unmodeled errors.Dazin,et al.15achieved active flow control by evenly arranging dozens of jets in the circumferential direction of a compressor to control the opening of the valve,so as to pump air into the compressor. It is noteworthy that this method has strict requirements for the design of efflux and actuator resulting in highly difficult mounting technique. In recent years, surge predictive control technology has also been developed with the more extensive application of predictive control in industrial processes.Such as Torrisi,et al.16are committed to applying Model Predictive Control (MPC) technology to the surge active control of industrial centrifugal compression system characterized by nonlinear dynamic characteristics with known component characteristics.Digital simulation has verified its advantages, but it is difficult to estimate the amplitude of pure input disturbance and ensure accuracy.When the component characteristics are known,Imani et al.successively presented surge control methods based on Tube-MPC,17explicit Nonlinear Model Predictive Control(NMPC),18,19and robust decentralized MPC20for the established extended Greitzer model considering pipelines with known component characteristics. These methods are respectively dedicated to solving the problems of unknown system characteristics and upper boundary disturbance,high computational complexity and real-time,and the surge problem of multi-compressor dynamic process under constraints. The simulation results show that the proposed method can achieve surge control well, but its robustness is poor, and oscillation occurs in the dynamic control process. Taleb Ziabari, et al.21,22studied the surge control method based on Tube-MPC for the established MG model with CCV of centrifugal compressor under unknown component characteristics. These methods approximate the component characteristics of the compressor through a fuzzy approximator to solve the problems of unknown component characteristics and unknown upper boundary disturbance.The simulation results show that the method solved the control variable constraint problem better than Ref. 12, But the control accuracy is not high. Subsequently, Imani Marrani et al.continued to study the robust Tube-MPC control method based on H-infinity control23and Linear Matrix Inequality(LMI) tool,24respectively. Through the additional designed state feedback control law, they are dedicated to stabilizing the states despite parametric uncertainty and disturbances and improving the calculation time and complexity.The simulation results showed that, compared with the robust adaptive tube-MPC, the proposed methods improved the control accuracy, but the error of fuzzy approximator in estimating the characteristics of unknown components easily leads to the failure of MPC control based on the state feedback of compressor model but not real compressor system. Through the above description of surge prediction method, they all did not consider the delay of sensors and actuators and the influence of measurement noise.

From the perspective of the control engineering application,the analysis of the above research reveals that these methods share a common defect, i.e., taking pressure and flow of compression system as the parameters that can be easily measured. However, only the pressure ratio is relatively easy to measure in engineering. Therefore, the flow is difficult to obtain. Although Sheng, et al.25designed a state observer through the pressure and its first derivation to solve the above problem, the estimation effect is poor without considering the effect of system uncertainty on the estimation result of the estimator.Molana,et al.26designed a state observer in accordance with circle criterion,but it is demanded by this method that the nonlinear vector-valued function of the unknown state in the system should be without coupling, and meet the condition of unilateral scalar sector; besides, it is also a nonsubtractive function exhibiting poor generality.

Surge active control allows the compressor to operate close to the surge line.Therefore,the reliability of the controller is of high significance.Once the controller is wrong,the compressor will enter the surge state directly,which partially explains why surge active control technology has not been applied practically. For instance, Sheng, et al.27fully considered the mentioned problem, and formulated an active/passive hybrid control strategy based on fuzzy logic. By default, the hybrid control system operates under the surge active control mode;once the surge active controller fails, the anti-surge controller immediately serves as the system backup mode to improve the reliability of the entire system. However, the mode switch is achieved by determining whether the controller fails in this control system,and the operating state of the compression system cannot be known. The decision criterion is limited, which cannot solve the fault of the actuator or system. For example,it is easy to face valve blocking and stuck due to long-term work,bad environment,as well as mechanical fatigue damage.Therefore, it is highly challenging to prevent and suppress the surge during surge active control of the compressor.28

Accordingly, this paper takes the axial compression system with CCV actuator as the control object. To overcome a considerable number of technical deficiencies in the existing surge active control methods such as the difficulty of flow measurement, dynamic uncertainty disturbances, actuator delay characteristics, hard constraints of control variable, and system security, a high-safety active/passive hybrid control approach for compressor surge is proposed in this paper, which is dominated by surge active control based on NMPC with flow estimator and supplemented by surge passive control. It mainly includes two parts: (A) a Nonlinear Model Predictive surge active Control method based on a flow estimator designed by using a Continuous-Time Kalman Filter (CTKF-NMPC)is presented to deal with the problems such as the difficulty of flow measurement,dynamic uncertainty disturbances,actuator delay characteristics,and hard constraints of control variable. Among them, the continuous-time Kalman filter is applied to improve the estimation accuracy of the mass flow.The nonlinear model predictive control deal with the hard constraints of control variable in the receding optimization step and handle the model mismatch (Actuator delay characteristics) and unknown disturbance (Dynamic uncertainty disturbance) in the feedback correction step; (B) The surge passive control is applied to handle the safety problems in the surge active control of compression system such as surge resulting from blocking and stuck of the valve, etc. When the compressor surge occurs, the surge detection algorithm will immediately send the warning signal to the anti-surge controller.The anti-surge controller drives the throttle valve to take the compressor out of the surge and operate in the stable area away from the surge line.As a result,the safety of active surge control of the compressor is guaranteed.

2. Surge dynamic model of axial compression system with CCV actuator

2.1. Mathematical model of axial compression system

According to the number of spatial coordinates describing the flow field, compression system models are generally classified into one-dimensional (1D), two-dimensional (2D), and threedimensional (3D) models. However, only the models of 2D and above can accurately predict and simulate the occurrence and development of the rotating stall, and show the regular pattern of the surge. The 2D MG model29and its optimized model are the most common axial flow compressor models capable of qualitatively capturing the nonlinear dynamic behavior of rotating stall and surge,which are effective in stability analysis and controller design.30In this paper, the second-order MG model simplified by using the GalerKin method31is selected as the mathematical model of the axial flow compression system.

The third-order MG model of the compression system is expressed by using the following three ordinary differential equations13,32,33:

where Ψ denotes the dimensionless pressure coefficient;φ represents the dimensionless mass flow coefficient;J expresses the first harmonic amplitude of flow fluctuation;lcand δ stand for the positive constant designed; and W refers to the half width of the cubic characteristic line; fC（φ） represents the steadystate characteristic curve of the compressor; fT（Ψ） represents the characteristics of the throttle valve; H represents half height of the cubic characteristic line.

The dimensionless time ξ is defined by the Helmholtz frequency (ωH).

where t denotes the actual time; a represents the sound speed;ACexpresses the equivalent channel area of the compressor;VPstands for the plenum volume; and LCrefers to the equivalent length of the compressor pipe.

The Greitzer stability parameter B that drives the compression system into/out of surge is defined as follows:

where U denotes the tangential velocity of the rotor.The Greitzer’s research suggested that when B＞Bcr(critical value of B), the instability type of the compression system is surge;while when B＜Bcr,the instability type of the compression system is rotating stall.

fC（φ） refers to the steady-state characteristic curve of the compressor, which can be approximated by using the cubic curve function:

Fig. 2 Schematic diagram of compression system with CCV.

where γTdenotes the parameter of the throttle valve.The nominal B parameter of the compression system can be changed by using the throttle valve,thereby altering the instability characteristics of the system.

Let J ≡0, the second-order MG pure surge model of the compression system is written as:

2.2. Mathematical model of actuator

The existing research on the active control of the turbomachinery compression system has been primarily conducted in the laboratory adopting different actuators34(e.g., inlet guide vane, loudspeaker, spring mass damper, momentum injection device,controllable control valve,throttle valve and close coupled valve). The response speed of the actuators (e.g., loudspeaker, momentum injection device and spring mass damper) can be hardly met and realized technically. This is because that the industrial compression system is characterized by a large flow rate,a high-pressure ratio and complex operating conditions,etc.Moreover,the inlet guide vane can be effectively adjusted to handle the rotating stall,which,however it is highly dependent on the technology. CCV can effectively mitigate the instability phenomenon,characterized by easy installation, fast adjustment speed and small time-delay. Therefore,it is confirmed to be suitable for complex industrial processes.35Accordingly, the research on the control model and control law of the CCV actuator is of high significance for achieving active control. In this paper, a throttle valve is adopted to change the operating condition of the compression system, and the active control law of the CCV is formulated for the control of the instability.

Fig. 2 depicts the schematic diagram of the compression system with CCV, in which the distance between CCV and the compressor outlet is small enough to assume that the mass flow storage between the two can be ignored.

As a mechanical actuator with time-delay phenomenon,the structural characteristics of CCV is described with a massspring-damping system. In addition, the transfer function of the actual output value of the CCV actuator relative to the command input value is written as:

Let x= ［Ψ φ］T,and set fV（Φ）as the compression system control variable u, then the nominal second-order MG compressor surge dynamic model is obtained as:

where the subscript ‘‘nom” indicates a nominal compression system model.

Like other physical systems, the uncertainties also exist in the compression system. Since these disturbances negatively affect the compression system, it is easy to cause instability of the compression system. In severe cases, the surge active controller can work abnormally. Therefore, the surge model considering uncertain external disturbances such as mass flow(dΦ（ξ）) and pressure (dΨ（ξ）) is act on the control object:

where the subscript‘‘real”indicates a real compression system;d represents the disturbances.

3.Nonlinear model predictive surge active control of compressor based on flow estimator

3.1. Design of flow estimator based on continuous-time Kalman filter

It is essential to take the pressure ratio and the mass flow of the compressor as the feedback parameters in the design of process of surge active controller. However, only the pressure ratio instead of the mass flow can be relatively easy to measure in engineering. To facilitate engineering implementation, a state observer should be designed to estimate mass flow through the input and pressure ratio. Currently, Kalman filter is considered as an optimal estimation algorithm,which can improve the estimation accuracy to the greatest extent by using the change law and measurement of the state itself. Thus, the second-order MG model is linearized to establish the statespace model. After that, a flow estimator is designed based on the continuous-time Kalman filter36to estimate the mass flow of the compression system with high-fidelity,thus solving the problem of difficult access to mass flow.

According to the Eq. (11), a nominal compression system model with the measurement output is expressed as:

where C=［1 0］, y which is not in bold indicates that only the pressure value is the output.

The first-order Taylor expansion of Eq.(13)is performed at a certain operating point(Ψ0， Φ0， γT0u0),and the approximate linearized state-space model is obtained as:

Secondly, based on the linearized state-space matrix A, the continuous-time Kalman filter is established to estimate the mass flow of the compression system as follows:

where R denotes output noise covariance matrix.

At last, the value of mass flow is accurately estimated by using the estimator based on the output pressure.

3.2. Nonlinear model predictive surge active control

3.2.1. NMPC principle

The NMPC37algorithm is a control algorithm based on nonlinear system model,which has the optimization mechanism of‘‘receding time domain, repeated in progress”,as illustrated in Fig. 3. This algorithm firstly uses the existing input-output data and prediction model to predict the output sequence of the future horizon; and the optimal control sequence is obtained through receding optimization of the designed demand cost function; subsequently, the first control element of the optimal control law sequence is selected to act on the system; the prediction model is then updated in the next control cycle. The above processes are repeated for receding optimization control. Based on the principle of the NMPC Algorithm,the following assumptions are made for the prediction model in the prediction horizon (np):

(1) Outside the control horizon (nc), the control variable is unchanged, i.e. Δuk+i=0， i=nc，nc+1，...，np-1.

(2) The measurable disturbance remains unchanged after time k, i.e. Δvk+i=0， i=1，2，...，np-1.

The following steps are repeated when the NMPC algorithm is applied in each control cycle:

Fig. 3 Schematic diagram of receding horizon optimization control.

Step 1. Measure the current state, and input it to NMPC controller as a feedback.

Step 2. Solve the discrete finite time-domain optimization problem by using receding optimization.

Step 3. Apply the first element of control sequence of the optimal solution to the system.

3.2.2. Design of surge active controller

(1) NMPC controller

According to the known state(xk)at the current k moment and control input sequence (uk，uk+1，...，uk+np-1) in the prediction horizon, the state and output of the system at the future horizon (np) can be predicted based on the Eq. (13).

Fig. 4 Active control structure with the NMPC algorithm of the compressor surge based on the flow estimator.

where fd，nom（·） denotes the discretization of fnom（·）, y^in bold indicates the estimated output as a vector of the mass flow and pressure.

Therefore, according to Eq. (26), the predicted output equation of the system at time k+i in the future can be recursively obtained as:

The compressor operates steadily in the surge boundary of the characteristic diagram, showing the stable pressure and mass flow. Therefore, taking the minimum error of the command pressure and mass flow value on the system stable tracking as the optimization objective, the performance objective function J（xk，u0:nc-1） is expressed as Eq. (29).

where ref denotes the reference value vector of pressure and mas flow; and u0:nc-1represents the control variable sequence with the control horizon(nc).The constraint is that each value of the control sequence should be greater than or equal to 0,i.e.,uk+i≥0， 0 ≤i ≤nc-1, where i refers to the sequence index of the control variable. According to the assumption of the prediction model, the control variable remains unchanged outside the control horizon, i.e .,Δuk+i=0（i=nc，nc+1，...，np-1）.

Eq.(29)suggests that it is a nonlinear optimization problem with hard constraints.Existing studies showed that the sequential quadratic programming algorithm38is considered as one of the most effective methods to solve constrained nonlinear optimization problems due to its advantages of good convergence,high computational efficiency and strong boundary search ability. Therefore, the objective function is optimized based on the above algorithm, and the specific principles are elucidated below:

where the superscript‘‘n”represents the index of the n-th iteration point; and u0:nc-1stands for the control sequence from 0 to nc-1.

Since the above problem is an approximate problem of the original constrained optimization problem, its solution may not be the feasible point of the original problem. Thus, let

Then, In this case, the nonlinear constraint problem (Eq.(29))is converted into the linear constraint quadratic programming problem. To simply the calculation during the optimization, the hard constraints of the control variable are introduced to the objective function in the form of penalty function (see Fig. 5) to convert the problem (Eq. (29)) into an unconstrained optimization problem, as expressed in Eq.(33).

Finally,a sequential quadratic programming algorithm can be adopted to solve unconstrained nonlinear optimization problems in a quick and easy manner.

Fig. 5 Hard constraint of control variable is transformed into penalty function (B（u）=（min（0，uk+i））2).

4. Design of a high-safety active/passive hybrid control system

4.1. Framework

A high-safety active/passive hybrid control framework of the designed compressor surge is illustrated in Fig. 6, which is dominated by surge active control and supplemented by surge passive control. The surge active control (the ‘‘black line”) is mainly used to achieve the compressor operate stably close to the surge line by controlling the CCV opening in realtime. However, the long-term operation, harsh environment and mechanical fatigue damage of the compression system may easily cause valve blocking and stuck. Consequently, the compressor directly enters the surge, which is not allowed.Accordingly, a surge detection and anti-surge control loop(the ‘‘red line”) with throttle valve control parameter (γTu) as the control value is designed as the surge passive control based on the surge active control of the compressor. It ensures that the compression system can return to the stable area in time after the occurrence of surge when the surge active control fails. Firstly, a surge detection algorithm based on the compressor outlet pressure signal is designed to monitor the operating state of the compressor in real-time, and then send out the surge warning signal. Secondly, according to this warning signal,the anti-surge controller sends control command to the throttle valve which is then opened to the maximum state.The compressor can therefore exit the surge state,and return to the stable area.

The control command signal sent by the surge control controller is mainly dependent on the surge warning signal sent by the surge detection algorithm, expressed as follows:

When sFlag = 0, → the compressor is in a stable state →the output command value of the anti-surge controller is γTu= 0;

When sFlag = 1, → the compressor is in a surge state →the output command value of the anti-surge controller is γTu= 0.2(maximum value).

As shown in Fig.6,γTdenotes the input parameter adopted to indirectly change parameter B,which can control the stability of the compressor;and γTurepresents the control parameter of the throttle valve output driven by the anti-surge controller.Once the compressor enters the surge,it will regulate and make the compressor exist from the surge and return to the stable operating area.

4.2. Compressor surge detection method

The development of a surge detection algorithm is critical to achieve surge passive control,which should be capable of accurately identifying the characteristics of compressor surge in real-time. Accordingly, the surge detection algorithm is designed by using the Hilbert-Huang transform time-frequency analysis method39based on the compressor outlet pressure signal. Firstly, the sliding window is adopted to process the compressor outlet pressure data. Secondly, the Empirical Mode Decomposition (EMD) algorithm is employed to solve the Intrinsic Mode Functions (IMFs) of the signal in the window for Hilbert transformation and time spectrum analysis.Thirdly, the statistics of the Compressor Surge Intensity(CSI) represented by the signal amplitude at the current moment is conducted (Eq. (41); Lastly, the compressor surge is detected by judging whether the CSI passes through the set threshold value.

where Ami（t）refers to the signal amplitude sequence obtained by the Hilbert time spectrum analysis, and i is the index.

The Hilbert-Huang transform time-frequency analysis method based on the compressor outlet pressure signal mainly consisted of three parts, and the specific implementation is expressed below:

Fig. 6 Framework of high-safety active/passive hybrid control framework of compressor surge.

(1) EMD Algorithm

EMD algorithm usually decomposes signals (p(t)) into a small number of IMFs. Residual signals must satisfy the following two conditions to be regarded as an Intrinsic Mode Function(IMF):(A)the number of extreme values(maximum and minimum values)and the number of zeros of the function must be equal or differ at most by one; (B) the local mean of upper and lower envelopes formed by each corresponding maximum point and minimum point, respectively, must be zero. The algorithm can be described as:

Step 1. Let k = 0 and find out all extreme points of the original signal (rk(t)): rk(t) = p(t).

Step 2. Obtain the upper envelope (emax) and the lower envelope (emin) of rk(t) by cubic spline interpolation.

Step 3. Calculate the envelope mean m(t): m(t) =(emax+ emin)/2.

Step 4. Subtract m(t) from rk(t)to acquire a residual signal(ck(t)) with low-frequency removed: ck(t) = rk(t) - m(t).

Step 5. Judge whether ck(t) is an IMF based on the above two conditions: if yes,save ck(t)and calculate the signal residual term rk+1（t）=p（t）-∑ki=1ci（t）, then let k = k + 1, and execute Step 2 with rk(t) as the input signal. Otherwise, return to Step 2, and let ck(t) as the next analysis signal.

Step 6. Continuously execute the decomposition cyclically until the signal residual term meets the end conditions of empirical mode decomposition.Specifically,the decomposition can be ended: when either the number of maximum points or the number of minimum points of the signal residual term is zero (mean conditions cannot be met), or when the remaining data is monotonic (the envelope cannot be made). Otherwise,return to Step 2 with the signal residual term.

The polar form of the analytic signal reflects the physical meaning of the Hilbert transform, implying that it obtains the local optimal approximation by frequency and amplitude modulation of the sine curve.

The above equations suggested that the amplitude and instantaneous frequency of the analytic function corresponding to each IMF can be obtained by the Hilbert transform for each IMF acquired by the EMD algorithm.

(3) Time-frequency spectrum analysis

After Hilbert transform for each IMF,the original signal p(t) can be expressed as:

where Re indicates the real part. The above mathematical expression reflects that the Hilbert-Huang transform is derived from the Fourier transform and manifests the relationship among signal amplitude, time and instantaneous frequency.The signal amplitude can be expressed as a function (H(ω,t))of time and instantaneous frequency, so as to acquire the signal amplitude, time and frequency distribution—Hilbert spectrum:

where H(ω,t) describes the change law of the signal amplitude with time and frequency at the whole frequency.

4.3. Stability analysis

In the case that the active control system is wrong,the passive control system will be activated and take its place.The throttle control input is adjusted to the maximum value to ensure the stable of the system. At this time, all control inputs remain unchanged,therefore it can be determined that the state equation of the system at this time is

Then the sufficient condition for the asymptotic stability of the system at the base point of state space given is that any positive definite real symmetric matrix Pm, including the following matrix.is a Lyapunov function of the system.

Proof. Considering that f（x） is an explicit function of ×instead of dimensionless time (ξ), there is the following relationship:

To make the system asymptotically stable, ˙V（x） must be negative definite, therefore Qm（x） must be positive definite.

In the case that Pm=I is selected,the joint Eq.(53)shows that.

Therefore,due to the fact that the system state matrix A is a negative definite matrix, and Qm（x） is a positive definite matrix, so the system is asymptotically stable.

5. Simulation and verification

According to the Section 2, the compression system model considering the time-delay of the sensor and actuator is established,and the relevant parameters are is listed in Table 1.13In this paper,four tests are simulated and compared to verify the robustness and effectiveness of the proposed method. The initial state value of the system is designed:Ψ=Φ=0.6,and it is assumed that the characteristics of the compression system components are known. Meanwhile, the following error criteria is defined to evaluate the advantages of the proposed method.

where y denotes the actual value; r stands for the reference value; error is the relative error that describes the deviation level of y from r.

5.1. Compressor surge simulation without controller

According to the Section 3, a flow estimator based on a Continuous-Time Kalman filter (CTKF) is established forthe estimation of the compressor mass flow in real-time. The initial relevant parameters of the flow estimator include:P=0·Inx,x^+=［0.6 0.6］,Q=0.00022Inx, and R=0.00022Iny, besides, the parameter of the actuator is:ωco=10.The sensor has a delay of one step,and its measurement noise is a normally distributed random number with v=2-4·rand（1）.

Table 1 Parameters value of the compression system.

During the simulation, the throttle valve parameter (γT) is directly adjusted for the direct change of parameter B, which makes the compression system enter the surge. As illustrated in Fig. 7(a), when ξ = 100, γTdecreased smoothly from 0.65 to 0.6. Moreover, the command pressure decreased smoothly from 0.6585 to 0.61, as depicted in Fig. 7(b), thereby making the compressor slowly transition from the steady-state zone to the surge zone. It can be seen from Fig. 7(c) that the flow estimator derived from based on the continuous-time Kalman filter can estimate the value of the output pressure and mass flow of the compression system based on the pressure residual(Δy)between the measured and calculated dimensionless pressure and by using the nominal compression system model.And the relative estimation error is±0.05%,while the relative estimation error of the estimator described in Ref.25 is±0.25%.Therefore, the flow estimator designed in this paper shows higher estimation accuracy. Subsequently, without any operations of the surge active controller, as the operating point of the compressor moves to the surge area, the compressor directly enters the deep surge state(ξ=190-400)after a rotating stall (ξ = 120-190). The system has a lower the stability,which cannot work statically in the surge boundary, as presented in Fig. 7(d).

5.2. Simulation of compressor surge active control without disturbances

Taking the flow estimated by the CTKF as the feedback value,a surge active controller(CTKF-NMPC)based on the NMPC algorithm is established to realize the surge active control of the nominal compression system and expand its operating range. It is assumed that the compression system has no dynamic uncertainty disturbances. The controller parameters include: np= 2, nc= 1, Qy= diag([10000 1]), Qu= 20,and ε= ［1 0］T(Note: These parameters can be chosen according to the law of Ref. 40).

To verify the robustness and effectiveness of the active control method described in this paper,a simulation comparison is made with the existing methods such as Robust Adaptive Backstepping active control of Compressor surge based on Wavelet Neural Network (RABC-WNN)13and Tube-MPCbased surge control.16,17,21-24

Firstly,without considering the delay of sensors and actuators and the measurement noise, CTKF-NMPC, RABCWNN,and Tube-MPC controller are compared in case of hard constraints on the control variable. The simulation results are shown in Fig. 8 below. It can be seen from Fig. 8(a) that all control inputs satisfy the requirement (u ＞0) when the constraints are considered. In Fig. 8(b), RABC-WNN controller has a better control effect with or without constraints, and the steady-state error is 0. Tube-MPC controller has a large disturbance during the dynamic change process,but it also stabilizes at a command value in the end, and the steady-state tracking error is±0.02%.Although CTKF-NMPC controller has a small deviation in tracking pressure in the dynamic process compared with RABC-WNN controller, it also has no steady-state error. As shown in Fig. 8(c), although there is a certain flow tracking error during the dynamic change of the target command at ξ= 100-200,the actual flow is completely tracked after ξ=200.Fig.8(d)shows that the system operates stably at the surge boundary under the action of the surge active controller.

Fig. 7 Simulation results of the compressor surge without active controller.

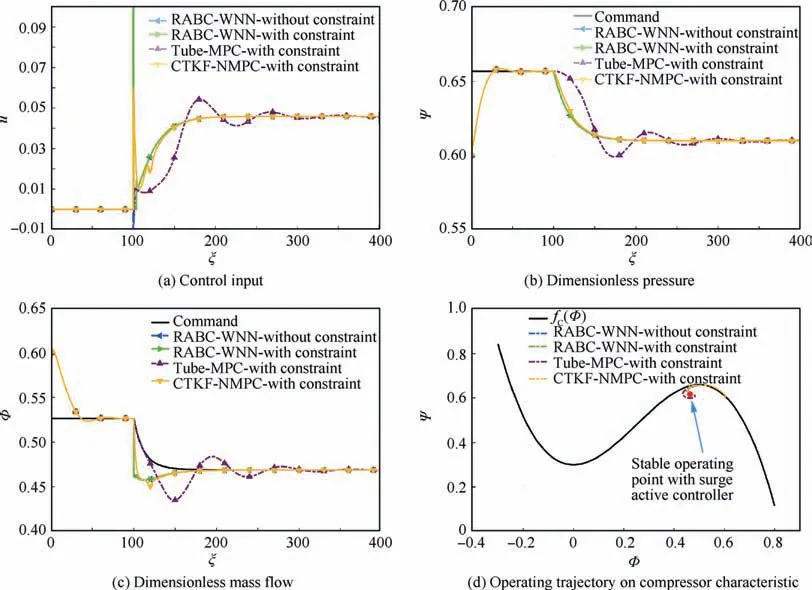
Fig.8 Simulation results of the compressor surge active control without disturbances in case of not considering the delay of sensors and actuators and the measurement noise.

Secondly, considering the delay of sensors and actuators and the measurement noise, the simulation results are shown in Fig. 9 below. The RABC-WNN controller is all wrong with/without considering constraints when the compression system begins to approach the surge boundary.And the system diverged. Although the Tube-MPC finally tracked the command pressure and stabilized the system, control input oscillated, and a negative value was generated at ξ = 100-250,resulting in flow oscillation. The CTKF-NMPC controller ensured the system’s stable operation without steady-state tracking error in case of meeting the control input constraints.Therefore, the results show that CTKF-NMPC controller has good robustness and is not affected by the delay of sensors and actuators and the measurement noise.

5.3. Simulation of compressor surge active control with disturbances

Based on the Section 5.1, the dynamic uncertainties disturbances (e.g., the disturbances of the pressure and mass flow)are imposed on the compression system, and the disturbance signal is written as13:

A controller designed with nominal system is adopted for the surge active control of the compression system with the dynamic uncertainty. Similarly, the simulation comparison is carried out with/without considering the delay of sensors and actuators and the measurement noise.

Firstly,Fig.10 showed the comparison results without considering the delay of sensors and actuators and the measurement noise. In Fig. 10(b), The RABC-WNN controller is effective without constraints but is wrong with constraints,leading to system diverging.The Tube-MPC controller tracked the command pressure under constraints and stabilized the system, but it fluctuated significantly in the dynamic and steady processes, with a range of about ±1.6%. The CTKF-NMPC controller ensured the system’s stable operation under the control input constraints.Due to the influence of disturbance,the steady-state tracking error of pressure is ±0.25%, and the steady-state tracking error of flow is ±5% (see Fig. 10(b)-(c)). The large steady-state mass flow control error is caused by the dynamic uncertainty disturbance in the system. On the other hand, it suffers a model error due to the mismatch of the real and nominal compression system, thus leading to a certain error(±2%)in the mass flow estimation.As a result,the controller has a higher flow control error than the pressure control. As depicted in Fig. 10(d), under the dynamic uncertainty disturbance, the surge controller designed based on the nominal compression system model can still achieve surge active control,and expand the operating range of the compressor.The comparison with Section 5.2 suggests that the CTKFNMPC with constraint is characterized by a better antiinterference ability and strong robustness.

Fig. 9 Simulation results of the compressor surge active control without disturbances in case of considering the delay of sensors and actuators and the measurement noise.

Fig. 10 Simulation results of the compressor surge active control with disturbances in case of not considering the delay of sensors and actuators and the measurement noise.

Secondly,considering the delay impact of sensors and actuators and the measurement noise, the simulation results are shown in Fig.11 below.The RABC-WNN controller is wrong with or without constraints,leading to system divergence.The Tube-MPC controller with constraint also caused the system to diverge and enter a surge. The CTKF-NMPC controller can still ensure the system’s stable operation under the condition of meeting the control input constraints. The steady-state tracking errors of pressure and flow are still ±0.25% and±5%, respectively. This shows that CTKF-NMPC has good robustness and is not affected by the delay of sensors and actuators and the measurement noise. It can well realize the surge active control of the compression system compared with the RABC-WNN and Tube-MPC.

To sum up, the comparative simulation results of Section 5.2 and Section 5.3 draw the following conclusions (see Table 2): the RABC-WNN controller is difficult to deal with the constraint problem in surge active control. Although Tube-MPC can deal with constraint problems, it leads to system divergence under the delay influence of sensors and actuators, measurement noise, and dynamic uncertainty disturbance. Therefore, compared with the methods described in the existing literature,the CTKF-NMPC controller can not only achieve high precision active surge control but also have better robustness.

Table 2 Comparison of surge active controller with considering the hard constraint.

5.4. Simulation of compressor surge active/passive hybrid control with disturbances

Fig. 10(a) and Fig. 11(a) show that when there is an uncertainty disturbance of the compression system, the controller can ensure the safe and stable operation of the system only by constantly adjusting CCV. Whereas CCV pertains to a mechanical actuator, which is capable of regulating the valve blocking and struck caused by mechanical fatigue damage,thus leading to the failure of the surge active control. Consequently, the compressor enters a surge. Fully considering the practical application of the surge active control method, a high-safety active/surge passive hybrid control strategy is designed,which is dominated by surge active control and supplemented by surge passive control. The surge passive control loop composed of surge detection and anti-surge controller is activated to issue control commands and adjust throttle control parameters to ensure the safety of the system.

Fig. 11 Simulation results of the compressor surge active control with disturbances in case of considering the delay of sensors and actuators and the measurement noise.

The surge detection algorithm based on the Hilbert-Huang transform is developed to monitor the compressor state.Fig. 12 presents the simulation results of the active/passive hybrid control strategy of compressor surge for considering the CCV fault. It is assumed that when ξ = 200, the realtime dynamic regulation of the CCV in the surge active control process is stuck and unable to be adjusted due to a mechanical fatigue damage, and the compressor soon enters a surge.Accordingly, the surge passive control governs, as illustrated in Fig. 12(a)-(b). When ξ = 246.5, the surge detection algorithm detects that the system is in a surge state and immediately sends a warning signal (sFlag = 1). The anti-surge controller then adjusts the throttle valve opening to allow the system to exit from the surge state and operate in the stable area. As illustrated in Fig. 12(d)-(e), after the compressor surge, due to the surge passive control, the system returns to the stable state without entering the deep surge. Fig. 12(f)shows that the surge active controller can make the compressor operate stably close to the surge line. While the surge passive controller ensures that the operating point is able to return to the stable operating area immediately after the occurrence of the surge of the compressor, and get away from the surge line for the safety of the system. The mass flow estimation error is within ±5% with the uncertainty disturbance. In the meantime, it can be seen in Fig. 12(c)-(f) that when there is no passive control, the system will suffer periodic surge.

The full consideration of the engineering application of surge active control of the compressor provides a solution to a series of problems (e.g., the difficulty of flow measurement,dynamic uncertainty disturbance, actuator delay characteristics, hard constraints of control variable, and system security measures). The results of the four simulation tests verified the effectiveness and robustness of the proposed highlysafety active/passive hybrid control approach for compressor surge based on the nonlinear model predictive control, thus ensuring the compressor’safe and stable operation to the surge line, and expanding its operating range. It has strong robustness.

Fig. 12 Simulation result of the compressor surge active/passive hybrid control with disturbances.

6. Conclusions

In this paper, a high-safety active/passive hybrid control method for compressor surge based on a nonlinear model predictive control is proposed to reduce the defects of the existing surge active control methods based on the practical application of compression system engineering. Fully considering the shortcomings of current surge active control methods, the following work has been carried out:

(1) The paper presented a nonlinear model predictive surge active control method of the compressor based on a flow estimator. Firstly, a flow estimator based on the continuous-time Kalman filter is designed to deal with the difficulty of flow measurement of the compression system in the actual process. The flow of the compression system is estimated with high-fidelity, and the estimation errors without and with disturbance are±0.05% and ±2%, respectively. Secondly, the surge active controller based on a nonlinear model predictive control is designed to handle the problems such as dynamic uncertainty disturbances, actuator delay characteristics, and hard constraints of control variable,etc. Finally, the above surge active controller is confirmed to have stronger robustness through the simulation test compared with the existing method; its steady-state control errors of the pressure without and with disturbance is 0% and ±0.25%, respectively, and the steady-state control errors of mas flow without and with disturbance is ±0.06% and ±5%, respectively.

(2) The long-term operation, harsh environment and mechanical fatigue damage of the compression system arising from the continuous adjustment of the valve during the surge active control, are found to cause valve blocking and stuck easily, thus leading to the compressor surge. A high-safety active/passive hybrid control strategy for compressor surge is developed, dominated by surge active control and supplemented by surge passive control,to ensure the constant and stable operation of the compression system. At last, the effectiveness of the proposed method is verified by the fourth test. The method can serve as a technical approach for the engineering application of compressor surge active control.

The proposed approach will be continuously explored to realize the engineering application in real-case compressor in the future.Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgements

This study was supported by the National Natural Science Foundation of China (Nos. 51906103 and 52176009).