车辆参数对车-桥耦合系统变截面连续梁桥损伤识别的影响

2023-02-09黄鹏飞李雪峰茆尚权

合肥工业大学学报（自然科学版） 2023年1期

黄鹏飞,李雪峰,茆尚权

(1.合肥工业大学土木与水利工程学院,安徽合肥 230009;2.中建四局第六建设有限公司,安徽合肥 230011)

近些年来,车-桥耦合振动理论取得较大发展,基于该理论的桥梁损伤识别方法也得到越来越多研究者的关注,与传统的静力损伤识别方法相比,这种动力损伤识别方法能够取得更好的识别效果。文献[1]通过对车辆加速度响应进行快速傅里叶变换,提取桥梁的一阶频率;文献[2]提出需要消除环境因素的干扰,得到的结构频率才会更精确;文献[3]用短时频域分解法处理车辆加速度响应,估算桥梁模态,通过数值案例可知,该方法对路面不平整度和噪声因素比较敏感,需要结合其他方式进行桥梁损伤识别,如对桥施加外部激励等;文献[4]将损伤识别与遗传算法相结合,通过车辆的加速度响应进行损伤定位与定量分析,并证明该方法在噪声和路面不平顺条件下也可以正常使用;文献[5]将灵敏度分析方法用于桥上运动车辆加速度信号的分析处理中,再结合最小二乘法和正则化方法对桥梁结构进行损伤识别,结果表明，该方法在路面不平顺和噪声等级较高的情况下,损伤识别效果并不理想;文献[6]对车辆的位移时程响应进行小波变换,数值算例表明,裂缝损伤程度越大越容易被识别,但对车速比较敏感;文献[7]将模态应变能和遗传算法相结合,提出一种多阶段损伤检测方法的理念,用车辆的振动响应成功实现两跨连续梁桥的损伤位置和损伤程度识别;文献[8]分析车辆悬架非线性和桥梁几何非线性对连续梁桥耦合振动响应的影响,结果表明,两者在一定程度上都能抑制桥梁的竖向跨中位移。

目前,桥梁损伤识别研究大多针对简支梁和等截面连续梁等简单桥梁结构,并且基本上都是从有限元软件直接提取振动响应数据。本文基于有限分段思想将变截面连续梁分成j个梁段,j→∞时可以将各梁段视为等截面,从而建立1/4车辆模型和变截面连续梁桥的耦合振动方程,然后在MATLAB环境下编制基于Runge-Kutta算法的车-桥耦合振动数值分析程序,得到桥梁跨中的竖向位移,最后结合桥梁结构损伤前、后振型函数及自振频率的变化,通过实际算例探讨车桥质量比、车辆速度、车辆弹簧刚度及信噪比4组参数的变化对损伤识别的影响。

1 车-桥耦合振动方程建立

1.1 车辆模型建立

1/4车辆模型如图1所示,将梁桥简化成梁单元模型,车辆简化为两自由度的弹簧-阻尼系统。图1中:mw为悬架和车轮的总质量;mv为车体质量;kw、cw分别为悬架体系的刚度和阻尼;kv、cv分别为车体的刚度和阻尼;yw、yv分别为悬架体系和车体的动挠度;y(x,t)为车辆作用点的动挠度。

图1 1/4车辆非线性模型

运用d’Alembert原理对悬架体系和车体进行受力分析。

1/4车辆模型的振动平衡方程用矩阵形式可表示为:

(1)

其中

1.2 桥梁模型建立

采用文献[9]分析方法建立变截面连续梁桥的动力平衡方程,根据有限分段思想在梁轴线位置处取长度为dx的单元体进行研究,假定轴向压应力FN为常值应力,且包含预应力V,其受力情况如图2所示。

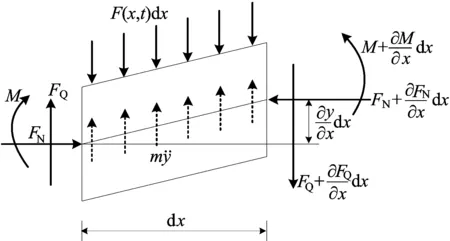
图2 梁单元体计算模型

根据该单元体竖向力和力矩的平衡,可得:

(2)

(3)

设u(x,t)、y(x,t)分别为梁上荷载沿x、y方向的位移,由Euler-Bernoulli梁理论可得:

(4)

y(x,z,t)=y0(x,t)

(5)

其中:u0(x,t)、y0(x,t)分别为中性轴上任意位置的轴向位移和横向位移;z为梁截面上某一点与中性轴的距离;t为时间。

混凝土梁的轴向应力较小,可忽略u0(x,t)的影响,根据梁的大位移小应变效应,其几何非线性关系式为:

(6)

其中,ξx为距梁起点x处的轴向应变。

根据文献[10]中Kelvin-Voigt模型,应力-应变本构关系为:

(7)

其中:σx为应力;E为梁的弹性模量;α为桥梁材料的黏性系数。

由σ-M关系式可得:

(8)

其中:b为截面宽度;h(x)为截面高度。

由σ-FN关系式可得:

(9)

联立(6)～(9)式,代入(3)式求解,得到剪力FQ,对FQ求关于x的偏导后代入(2)式,可得:

(10)

1.3 车-桥耦合方程的建立与求解

令r(x)为桥面不平整度函数,x为车辆在桥上的位置,则车辆对桥的作用力P(t)、F(x,t)为:

P(t)=(mv+mw)g-kw[yw-y(x,t)-

(11)

F(x,t)=δ(x-vt)P(t)

(12)

其中:δ为Dirac函数;v为车辆行驶速度。将y(x,t)按照振型分解法分离变量后可得:

(13)

其中:Φi(x)、qi(t)分别为梁的第i阶模态函数和模态坐标。

运用振型分解法进行求解,然后用伽辽金法进行化简,整理后的结果联立(3)式,可得变截面连续梁桥的车-桥耦合振动方程为:

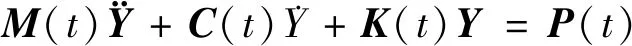
(14)

其中:M(t)为(N+2n)阶广义的车-桥耦合质量矩阵,N为桥梁振动方程所取阶数,n为车辆数;C(t)为(N+2n)阶广义阻尼矩阵;K(t)为(N+2n)阶广义刚度矩阵;P(t)为(N+2n)阶车-桥耦合作用外力向量;Y为(N+2n)阶车-桥耦合位移向量。

(14)式为时变的二阶非线性微分方程组,所取阶数越大,计算精度越高,但工作量也相应变大,经试算可知,选取前3阶振型可以兼顾精度和工作量。本文采用MATLAB编制基于Runge-Kutta算法的耦合振动模拟程序进行求解,模拟流程如图3所示。

图3 车-桥耦合振动模拟流程

2 车辆参数对桥梁损伤识别的影响

以某三跨混凝土连续梁桥为例。桥梁参数如下:桥梁跨径为(27.92+42.00+27.92) m;梁体为C50混凝土,弹性模量E=34.5 GPa;混凝土密度ρ=2.5×103kg/m3,泊松比ν=0.2。箱梁跨中、支点处横截面尺寸分别如图4、图5所示(单位为cm)。

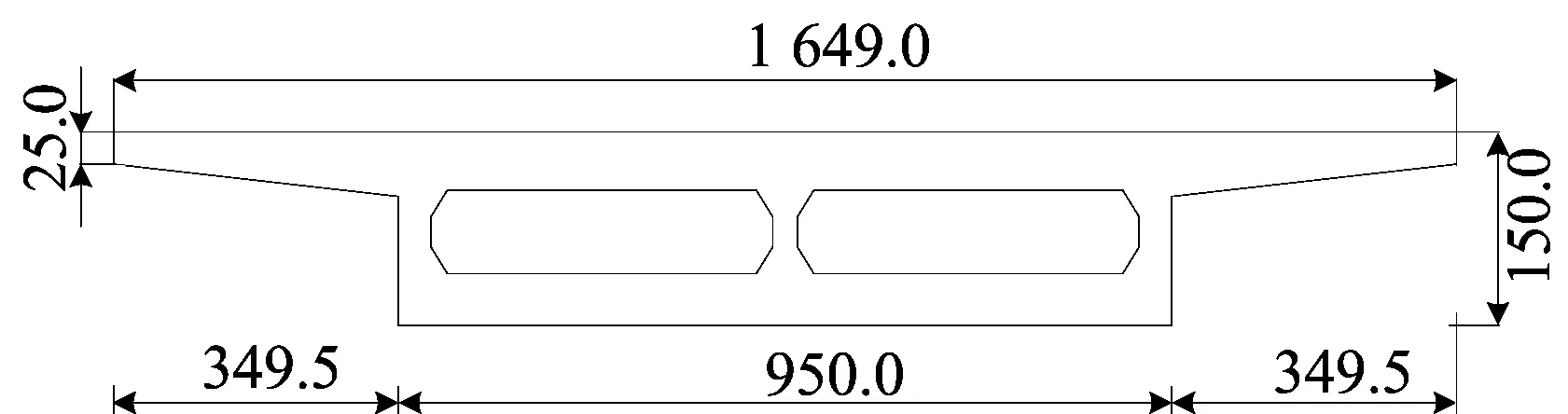
图4 箱梁跨中横截面

图5 箱梁支点横截面

车辆参数如下:车身质量mv=3.85×104kg;车身与悬架系统之间弹簧刚度kv=5.07 MN/m,阻尼cv=3.82×105kg/s;车辆悬架与车轮的总质量mw=8.66×103kg;车辆悬架与车轮系统弹簧刚度kw=8.56 MN/m,阻尼cw=1.96×105kg/s。

2.1 不同车桥质量比对桥梁损伤识别的影响

工况1 假定桥梁损伤位于中跨跨中附近位置,损伤程度取抗弯刚度折减40%,车辆移动速度设定为10 m/s,桥梁模型总质量为2 486.59 t,车辆模型总质量为10 t,车桥质量比为0.004,车辆其他参数不变,分别计算无损伤、中跨受损伤桥梁的跨中竖向位移响应,结果如图6所示。

图6 车桥质量比为0.004时无损伤、受损伤桥梁跨中竖向位移

由图6可知,当车桥质量比为0.004时,无损伤、受损伤桥梁的跨中竖向位移响应曲线波动明显,且十分相似,竖向位移响应曲线几乎重合或基本一致,无法清晰识别出桥梁是否受到损伤。

工况2 车辆系统总质量增加到30 t,车桥质量比为0.012,其余参数同工况1,位移响应如图7所示。

由图7可知,车桥质量比提高为0.012,无损伤、受损伤桥梁的跨中竖向位移响应曲线波动明显变弱,竖向位移响应曲线十分接近,但是跨中位移开始出现差异,在车辆行驶到桥梁受损伤位置处差异最为明显。随着车桥质量比增大,桥梁的第1跨跨中和中跨跨中的竖向位移响应也随之变大,且数值变化程度十分明显,其中无损伤、中跨受损伤桥梁的中跨跨中曲线第2峰峰值分别为-2.563、-2.670 mm,两者相差0.107 mm。

工况3 车辆系统总质量提高到50 t,车桥质量比为0.020,其余参数同工况1,位移响应如图8所示。

由图8可知,车桥质量比达到0.020,桥梁跨中竖向位移响应曲线的波动继续变弱,曲线更加平滑,无损伤、受损伤桥梁的第1跨跨中竖向位移响应曲线在桥梁局部位置开始出现微弱的偏差,桥梁的中跨跨中位移响应曲线出现明显的差异,且响应数值进一步变大,无损伤、受损伤桥梁的中跨跨中曲线第2峰峰值分别为-4.201、-4.357 mm,两者相差0.156 mm。

图8 车桥质量比为0.020时无损伤、受损伤桥梁跨中竖向位移

由图6～图8可知,车桥质量比的改变对车-桥耦合振动损伤识别有影响,车桥质量比的不断增大对桥梁跨中竖向位移响应曲线的整体趋势没有太大影响,无损伤桥梁和中跨受损伤桥梁是在几乎相同位置达到曲线峰值,且曲线的波动不断减弱,曲线的波动是由路面不平整因素引起的,由此可知,增大车桥质量比对路面不平整因素有抑制作用。随着车桥质量比增加,桥梁跨中竖向位移数值增大,无损伤桥梁和中跨受损伤桥梁的中跨跨中竖向位移响应差值也增大,中跨受损伤桥梁更容易被识别。因此,在车-桥耦合振动识别变截面连续梁桥损伤研究中,应该选取车桥质量比大的车辆模型。

2.2 不同车速对桥梁损伤识别的影响

工况4 假定桥梁损伤位于中跨跨中附近位置,损伤程度取抗弯刚度折减40%,车辆模型总质量取初始参数47.16 t,车速10 m/s匀速驶过无损伤和中跨受损伤连续梁桥,其他参数不变,第1跨和中跨跨中竖向位移曲线如图9所示。

图9 车速10 m/s时无损伤、受损伤桥梁跨中竖向位移

由图9可知,车辆以10 m/s匀速通过桥梁时,无损伤、、中跨受损伤桥梁的第1跨跨中竖向位移响应、中跨跨中竖向位移响应的波动是一致的,都在相同的位置附近达到波峰、波谷。车辆分别在无损伤和中跨受损伤桥梁上行驶,行驶到第1跨跨中位置时,第1跨跨中竖向位移响应曲线有小幅的变化,但不是很明显,此时中跨跨中竖向位移响应曲线几乎没有变化;车辆继续行驶,当行驶到中跨跨中位置即损伤位置时,第1跨跨中竖向位移响应曲线很难观察到区别,但是中跨跨中竖向位移响应曲线变化差异明显,无损伤、受损伤桥梁中跨跨中曲线第2峰峰值分别为-3.968、-4.126 mm,两者差值为0.158 mm。

工况5 提高车速至20 m/s,其余参数不变,竖向位移曲线如图10所示。

由图10可知,车辆以20 m/s匀速通过桥梁时,无损伤、受损伤桥梁的第1跨跨中竖向位移响应、中跨跨中竖向位移响应也具有相似的规律性,但和10 m/s匀速通过桥梁时的位移响应曲线有所区别,速度的提高使桥梁跨中竖向位移响应曲线的波动明显变弱。车速的提高使得桥梁跨中竖向位移响应曲线峰值发生相应变化,无损伤、受损伤桥梁的中跨跨中曲线第2峰峰值分别为-4.001、-4.163 mm,两者差值为0.162 mm。

图10 车速20 m/s时无损伤、受损伤桥梁跨中竖向位移

工况6 继续提高车速至30 m/s,其余参数不变,竖向位移曲线如图11所示。

由图11可知,车辆以30 m/s匀速过桥,跨中竖向位移响应依然具有相似性,并且位移响应曲线波动继续变弱。车速的提高使中跨跨中竖向位移响应曲线第2峰峰值的差值进一步扩大为0.185 mm,但是曲线峰值出现位置却向桥头方向移动,对车-桥耦合振动变截面连续梁桥损伤识别造成一定的干扰。

由图9～图11可知:车速的改变并没有影响桥梁跨中竖向位移响应变化规律,竖向位移响应具有相似性,曲线的波峰、波谷位置十分接近。随着车速不断提高,中跨跨中竖向位移曲线第2峰峰值的差值不断增大,但差值的增大幅度较小,车速10 m/s时差值为0.158 mm,车速30 m/s时差值为0.185 mm,仅相差0.027 mm,对桥梁损伤识别研究的影响不大;同时速度提高使桥梁跨中竖向位移响应曲线的波动性变弱,跨中竖向位移响应的峰值也向桥头方向移动,对损伤识别研究造成一定的干扰。在实际试验中,车辆行驶速度越快,外界的干扰越多,信号数据的采集越困难,会导致采集的数据不准确,因此在车-桥耦合振动识别变截面连续梁桥损伤后续研究中,采用行车速度为10 m/s。

图11 车速30 m/s时无损伤、受损伤桥梁跨中竖向位移

2.3 不同弹簧刚度对桥梁损伤识别的影响

工况7车身与悬架系统之间弹簧的刚度kv、车辆悬架与车轮系统弹簧的刚度kw取值均为500 kN/m,车速设定为10 m/s,其他参数不变,匀速驶过无损伤桥梁和受损伤桥梁,计算第1跨跨中和中跨跨中竖向位移响应曲线,结果如图12所示。

由图12可知,当车辆弹簧刚度为500 kN/m时,桥梁跨中竖向位移响应曲线的波动较微弱,曲线总体平滑,在局部位置有小幅振动。从图12b可以看出,无损伤、受损伤桥梁曲线几乎重合,仅在受损伤单元附近出现差异,两者第2峰峰值分别为-3.917、-4.061 mm,两者差值为0.144 mm。

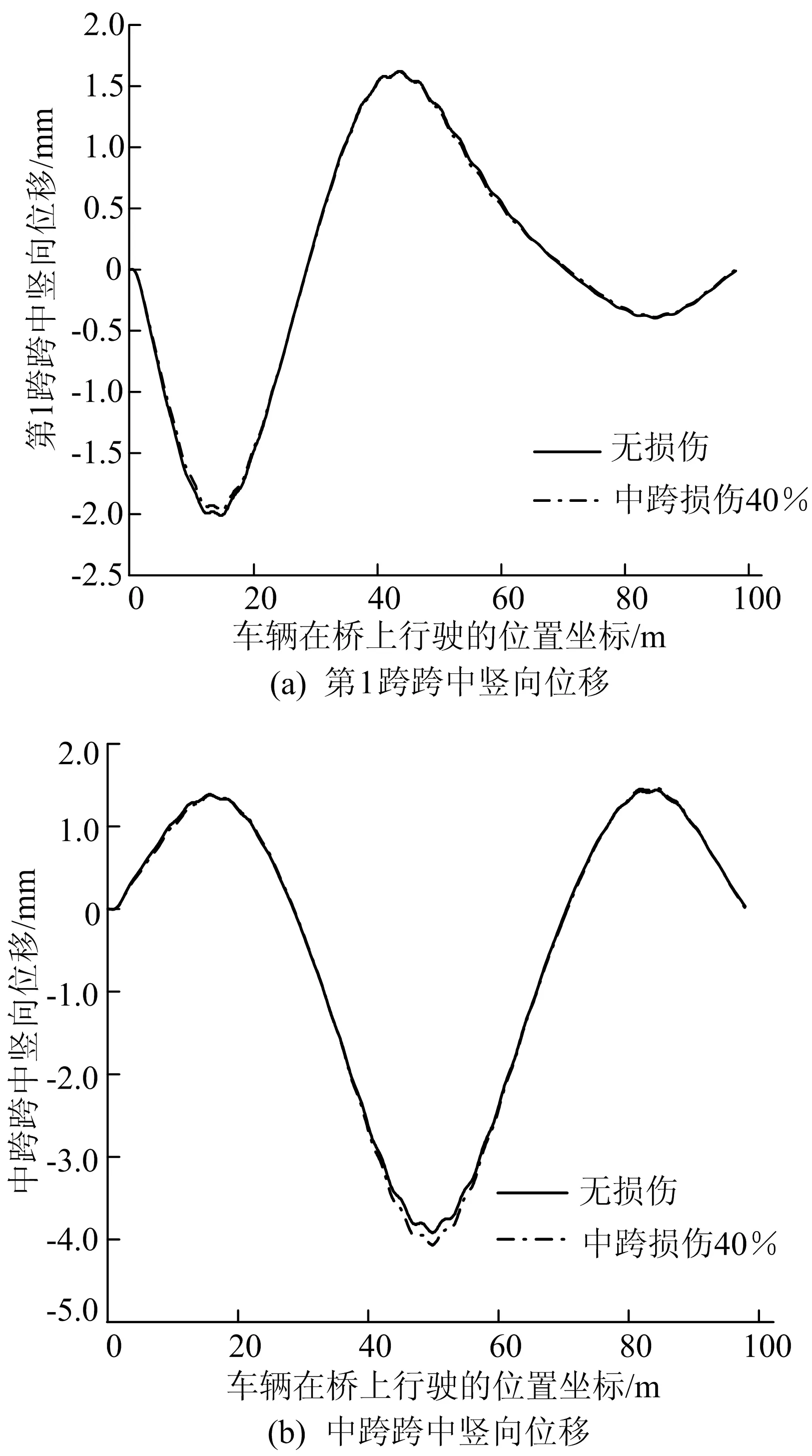
图12 kv、kw为500 kN/m时无损伤、受损伤桥梁跨中竖向位移

工况8 车辆系统弹簧刚度为5 000 kN/m,其余参数同工况7,跨中竖向位移响应如图13所示。由图13可知,车辆系统弹簧刚度的增加使得桥梁跨中竖向位移响应曲线的波动稍变大,但没有影响曲线整体的波动趋势。由图13b可知,无损伤、受损伤桥梁的曲线第2峰峰值依然存在差距,两者分别为-3.936、-4.080 mm,两者差值为0.144 mm,和工况7的差值一样,没有变化。

图13 kv、kw为5 000 kN/m无损伤、受损伤桥梁跨中竖向位移

工况9 车辆系统弹簧刚度为50 000 kN/m,计算得到桥梁跨中竖向位移响应,如图14所示。

从图14可以看出，车辆系统弹簧刚度提高到50 000 kN/m后,桥梁跨中竖向位移响应曲线的波动性明显增强,但2种情形的曲线几乎重合,无明显差异,很难进行损伤识别研究。

图14 kv、kw为50 000 kN/m无损伤、受损伤桥梁跨中竖向位移

由图12～图14可知,改变车辆系统弹簧刚度后，桥梁跨中竖向位移曲线总体走向没有改变,但是提高弹簧刚度使曲线波动性变得更加明显,曲线的波动性与路面不平整度相关,可知车辆系统弹簧刚度的升高对路面不平整因素有放大作用。对比工况7和工况8,无损伤、受损伤桥梁中跨跨中竖向位移响应曲线第2峰峰值差值大小一样,说明在一定范围内,弹簧刚度参数对车-桥耦合振动识别桥梁损伤的影响很小,可以忽略不计。

2.4 不同信噪比对桥梁损伤识别的影响

车-桥耦合振动得到的位移响应存在噪声的影响,因此在图3流程中生成的位移响应部分加入不同信噪比下的高斯白噪声,分析噪声对桥梁损伤识别的影响。信噪比RSN计算公式为:

(15)

其中:y(i)为纯信号序列;z(i)为高斯白噪声序列;Q为项数;i为从1开始增大到Q的整数。

车辆模型总质量取初始参数47.16 t,车速取10 m/s,车辆系统弹簧刚度取500 kN/m,采样频率为100 Hz,信噪比取20、30、40 dB,刚度折减40%,计算无损伤、中跨受损伤桥梁的跨中竖向位移响应,结果如图15所示。

图15 3种信噪比条件下无损伤、受损伤桥梁跨中竖向位移

由图15可知:当信噪比为20 dB时,位移响应被噪声所淹没,信号完全失真;当信噪比增加到30 dB时,曲线的细节波动性明显降低,无损伤、受损伤桥梁跨中位移开始出现差异,当车辆行驶到桥梁跨中受损伤位置时差异最为明显,两者峰值相差0.165 mm,比无噪声时大0.021 mm,说明在一定情况下噪声可以对位移响应产生影响;当信噪比进一步提高为40 dB时,曲线逐渐逼近图12b中的无噪声曲线,细节波动性进一步降低,无损伤、受损伤桥梁跨中位移差异更加明显,2条曲线第2峰峰值分别为-3.994、-4.159 mm,两者差值为0.136 mm,损伤识别效果比无噪声时低0.008 mm,可以忽略不计。综上可以看出,随着信噪比提高,位移响应曲线逐渐逼近于无噪声曲线,损伤识别效果也越来越好。