四元域上一类厄米特互补对偶常循环码
2023-02-09孙世林
孙世林,刘 丽
(合肥工业大学 数学学院,安徽 合肥 230601)
0 引 言
常循环码是一类重要的线性码,在纠错码理论中占有重要的地位[1-2]。常循环码可以通过移位寄存器进行有效编码,是工程应用中优先选择的对象。
线性码C若满足C∩C⊥={0}则称C为线性互补对偶码(linear codes with complementary duals,LCD)。文献[3]首次引入有限域上LCD码,证明了LCD码是渐近好码;文献[4]证明了二元LCD码可以用于密码边道攻击,这引起了学者们对构造LCD码的极大兴趣;文献[5]构造了有限域上几类LCD循环码并分析了它们的参数;文献[6]分析了可逆BCH码的参数;文献[7]分析了有限域上可逆负循环BCH码的几类参数。
但是很少有学者研究厄米特LCD码。文献[8]研究了基于欧几里得和厄米特LCD码的准循环LCD码的性质,证明了这些码是渐近好码;文献[9]利用生成矩阵给出了厄米特LCD码的一个充要条件。
最近,文献[10]利用维数比较小的线性码、自正交码和广义的RS码构造出几类新的欧几里得和厄米特LCD MDS码;文献[11]构造出几类厄米特LCD循环码并分析了它们的参数。
本文目的是构造四元厄米特LCD常循环码,并分析它们的参数,确定这些码的维数,给出它们最小距离的下界。本文提出的厄米特线性互补对偶码不是常循环BCH码。
1 预备知识

C⊥H={(b0,b1,…,bn-1)∈GF(4)n:
定义1[9-11]设C为GF(4)上一个长为n的线性码,且C⊥H为C的厄米特对偶码,若C⨁C⊥H=GF(4)n或C∩C⊥H={0},则称码C为厄米特LCD码。
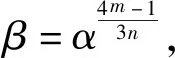
引理1[2,12]假定gcd(3,n)=1,设C=〈g(x)〉为GF(4)上长为n的ω-常循环码。若g(x)的根为{β1+3i|0≤i≤δ-2},则C的最小距离d≥δ。
设mi(x)表示GF(4)上βi的极小多项式。用imod 3n表示在集合{0,1,2,…,3n-1}中与imod 3n同余的唯一整数。记
mi(x)=mi mod 3n(x),
对于整数δ≥2,定义:
g(n,δ,1)(x)=lcm(m1(x),m4(x),…,
m1+3(δ-2)(x))
(1)
其中,lcm表示多项式的最小公倍数。设C(n,δ,1)表示生成多项式为g(n,δ,1)(x)且长为n的ω-常循环码,由引理1,码C(n,δ,1)的最小距离至少为δ。
设Z3n={0,1,2,…,3n-1}。∀s∈Z3n,4模3n含s的分圆陪集定义为:
Cs={s,4s,42s,…,4ds-1s}mod 3n⊆Z3n,
其中,ds为满足s4ds≡smod 3n的最小正整数,且Cs中有ds个元素。
设T={1+3i|0≤i≤n-1}⊆3n,Cs中最小整数称为Cs的陪集首。对于∀s∈Z3n,显然有T∩Cs=Cs或{0}。
设Γ(n,4)为T∩Cs=Cs所有陪集首的集合。∀s,t∈Γ(n,4),s≠t,有Cs∩Ct={0}且
(2)
βs在GF(4)上的极小多项式ms(x)可表示为:
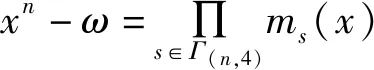

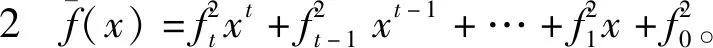
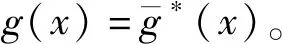
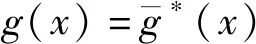
2 四元厄米特LCD常循环码的结构
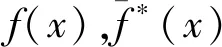
(3)
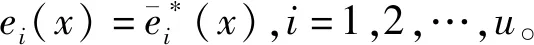
定理1 设C为GF(4)上长为n的ω-常循环码,且生成多项式为:
g(x)=e1(x)a1e2(x)a2…eu(x)auf1(x)b1×
其中,ai,bj,cj∈{0,1},则C为四元厄米特LCD码当且仅当bj=cj,j=1,2,…,v。因此,长为n的四元厄米特LCD常循环码总数为2u+v。
证明由引理1和引理2可得。
定理1指出长为n的四元厄米特LCD常循环码的个数由(3)式决定,指明四元厄米特LCD常循环码定义集的结构特点,它应具有以下类型:
S={s∈T:g(βS)=0},

类似于文献[11]中定理4,可以得到下面定理。
定理2 设C是GF(4)上长为n的ω-常循环码,其生成多项式为g(x),则C为厄米特LCD码,当且仅当下面条件之一成立。
(1) 对于C的定义集S,S=-2S,其中,-2S={-2s:s∈S}。
(2) 对于每个g(x)的根β,β-2也是g(x)的一个根。
定理3 长为n的四元ω-常循环码都是厄米特LCD码充要条件为-1是2 mod 3n的奇幂。
证明一方面,设-1≡22t+1(mod 3n),t≥0。因为对于每个a∈T有-a≡a·22t+1(mod 3n)且-2a≡a·22t+2≡a·4t+1(mod 3n),所以-2a∈Ca,即fj(x)不在(3)式中出现。由定理1可知,在GF(4)上每个长为n的ω-常循环码是厄米特LCD码。
另一方面,设β为3n次本原单位根,m1(x)表示GF(4)上β的极小多项式。设C为GF(4)上长为n且生成多项式为m1(x)的ω-常循环码,若C是厄米特LCD码,则-2∈C1且-2≡4t(mod 3n),其中,1≤t≤m-1,3n是奇数,因此,-1≡22t-1(mod 3n)。
3 长为(4m-1)/3的四元厄米特LCD码
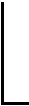
由定理3,设n=(22t+1+1)/3,易证m=2t+1。由引理3,1是4模22t+1+1的分圆陪集的陪集首。
下面通过常循环BCH码构造长为n=(4m-1)/3的四元厄米特LCD码且分析其参数。设
g(x)=lcm(g(n,δ,1),m3n-2[1+3(δ-2)](x),
m3n-2[1+3(δ-3)](x),…,m3n-8(x),m3n-2(x))
(4)
其中
g(n,δ,1)=lcm(m1(x),m4(x),…,
m1+3(δ-3)(x),m1+3(δ-2)(x))。

下面的引理是关于4模3n的分圆陪集的性质。
引理5[11]设n=(4m-1)/3,i表示4模3n的分圆陪集Ci的陪集首,则有:
(1) |Cn-2i|=|Ci|。
(2)Cn-2i=Cn-2j当且仅当Ci=Cj。
(3)Cn-8i=Cn-2i。
设C为GF(4)上长为n且生成多项式为g(x)的ω-常循环码,C的定义集可以表示成:
记
显然
-2(1+3a)≡3n-2(1+3a)mod 3n,
-2[3n-2(1+3a)]≡4(1+3a)mod 3n。
因此,S=-2S。由定理2,C是GF(4)上厄米特LCD码。


(2) 当m为奇数时,有
|J+(δ)∩J-(δ)|=
(3) 当m为偶数时,有
|J+(δ)∩J-(δ)|=0。


同理,有


a∈J+(δ)∩J—(δ),
则存在i、j,0≤i,j≤δ-2,使得:
a∈C1+3i=C3n-2(1+3j),
故有:
1+3i≡-2(1+3j)4lmod(4m-1),
即
1+3i+(1+3j)22l+1≡0 mod(4m-1)
(5)
设1+3i,1+3j的2-adic展开分别为:
1+3i=im2m+im-12m-1+…+i12+i0,
1+3j=jm2m+jm-12m-1+…+j12+j0,
0≤ik,jk≤1,0≤k≤m,(i0,i1)≠(0,0),
(j0,j1)≠(0,0)。
情况1当1≤l≤(m-3)/2时,0<1+3i+(1+3j)22l+1<4m-1,则
1+3i+(1+3j)22l+1≡0 mod(4m-1)
不成立。
情况2 当l=(m-1)/2时,可证明1+3i+(1+3j)22l+1≡Δmod(4m-1),其中
Δ=jm-122m-1+…+j12m+1+(j0+im)2m+
im-12m-1+…+i12+(i0+jm)。
注意0<Δ<6n,由(5)式得Δ=3n。因此,jm-1=…=j1=j0+im=im-1=…=i1=i0+jm=1,则im=u,jm=v,i0=1-v,j0=1-u,其中,u,v=0,1。因此,1+3i=(u+1)2m-v-1,1+3j=(v+1)2m-u-1。
情况3 当(m+1)/2≤l≤m-1时,有
m+2≤2l+1≤2m-1。
令2l+1=m+ε,2≤ε≤m-1,则1+3i+(1+3j)22l+1≡Δmod(4m-1),其中
Δ=jm-ε-122m-1+…+j12m+ε+1+j02m+ε+
im2m+…+iε+12ε+1+(iε+jm)2ε+…+
(i1+jm-ε+1)2+(i0+jm-ε)。
Δ的2-adic展开中2m+1的系数为0。因此,0<Δ<3n。这种情况下(5)式是不成立的。
情况2中,i=iuv且j=juv。集合L为:
1+3iuv=(u+1)2m-v-1,
注意情况1~情况3包含全部使C1+3i=C3n-2(1+3j)的可能数对(1+3i,1+3j),0≤i,j≤δ-2,其中,2≤δ≤(2m+1-1)/3+2。于是有:
(6)
由引理4,1+3iuv为陪集首,由引理5,C3n-2(1+3a)≠C3n-2(1+3b)当且仅当C1+3a≠C1+3b。因此(6)式中并没有交集,则有:
|J+(δ)∩J—(δ)|=|L|m。
因为u,v=0,1,所以1+3iuv、1+3juv都分别可能等于2m-1、2m-2、2m+1-1、2m+1-2这4种情况。因为2m-2、2m+1-1、2m+1-2不具有1+3i的形式,所以舍去。于是,1+3iuv=2m-1,1+3juv=2m-1。
当1+3iuv<2m-1时,即1+3(δ-2)<2m-1,|L|=0。于是有:
|L|=
当m为偶数时可用同样的方法证明。

证明由定义1,C的生成多项式g(x)的次数等于|J+(δ)|+|J-(δ)|-|J+(δ)∩J-(δ)|,维数k=(4m-1)/3-deg(g(x)),则由定理4可得。
例1 设m=3,δ=5,C是GF(4)上长为21的ω-常循环码,其生成多项式为:
g(x)=m1(x)m7(x)m10(x)m61(x)m43(x)=
x15+x14+ωx13+x12+x11+x9+ωx8+ωx7+
ω2x6+ω2x4+ω2x3+ωx2+ω2x+ω2,
则C是GF(4)上参数为[21,6,12]的厄米特LCD码。
例2 设m=3,δ=2,C是GF(4)上长为21的ω-常循环码,其生成多项式为:
g(x)=m1(x)m61(x)=x6+ω2x5+x4+
ω2x2+x+ω2,
则C是GF(4)上参数为[21,15,5]的厄米特LCD码。
例3 设m=4,δ=4,C是GF(4)上长为85的ω-常循环码,其生成多项式为:
g(x)=m1(x)m7(x)m253(x)m241(x)=
x16+x15+ωx14+x12+ωx11+ωx9+
ω2x8+x7+x5+ωx4+x2+ωx+ω,
则C是GF(4)上参数为[85,69,5]的厄米特LCD码。
4 结 论
本文构造了四元厄米特互补对偶常循环码,并分析它们的参数。确定长度为n=(4m-1)/3的厄米特LCD常循环码的维数,给出了它们最小距离的下界。本文仅分析了长度为n=(4m-1)/3的四元厄米特互补对偶常循环码的参数,其他长度也有待进一步探讨。
