基于优先因子的最佳供应方案和最大产预测模型
2023-02-09向福川练瑶唐振云王建宏
文/向福川 练瑶 唐振云 王建宏
本文主要研究生产企业的原材料订购与运输问题。首先,以压缩生产成本为首要考虑,确定选取供应商应该为题目中所有供应商,在这里引入优先因子,将订购方案的类目标规划问题分解成一系列单目标规划问题依次进行求解,再对订购方案和转运方案的实施效果进行分析。再研究该企业具备了通过一定的技术改造方法提高产能的潜力。通过确定企业理论的最大产能上限,采用二分法原理进行求解,得到产能的实际最大值,给出未来24周的订购方案与转运方案。
一、引言
厂商在原材料运输时应综合多方面选择合理的运输方案,例如控制原理及成品、半成品运输成本的运输方法,从运营成本控制方面寻求更多的节流方式[1]。因此我们对前几年供货商供货数据、技术优势及长期供货能力以及厂家需求的数据经行综合分析是非常有必要的,有利于保障企业的各项生产计划和企业效益最大化。本文对2021年全国大学生数学建模竞赛C题[1]的问题3、问题4,问题3需要在考虑生产成本的基础上,解决订购方案和转运方案的制定问题,并对制定的订购方案和转运方案的实施效果进行分析。问题4需要根据现有原材料的供应商和转运商情况,确定企业产能的最大值,同时给出未来24周的订购方案与转运方案。
二、模型准备
问题3要以压缩生产成本为首要考虑,所以对于问题3、问题4的供应商的选取范围应该为402家供应商。在解决方案制定问题时,考虑到A、B、C三类原材料生产单位产品需消耗的原材料量存在差异,即在满足生产需求且达到相当产能的条件下,A、B、C三类原材料的订购量将直接影响到企业的生产成本,容易知道尽量多地采购A类和尽量少地采购C原材料,可以达到压缩成本的目的。因而,对于新订购方案的制定,需要增加描述多选择A类原材料、少选择C类原材料的约束条件,考虑在这里引入优先因子,为A、B、C类原材料的采购行为排定优先级的先后次序,将订购方案的类目标规划问题分解成一系列单目标规划问题依次进行求解。在对订购方案和转运方案的实施效果进行分析时,与问题2类似,将订购量与实际供货量、供货量与实际接收量进行对比,分析方案实施的可行性与融洽性。问题4指出该企业具备了通过一定的技术改造方法提高产能的潜力,即此时企业的产能仅与现有原材料的供应商和转运商的实际情况有关,具体来说,就是企业产能的提高取决于供应商的供货能力(供货稳定性、最大供货量)和转运商的转运能力(运输能力、转运损耗率)。通过确定企业理论的最大产能上限,采用二分法[4]原理进行求解,得到产能的实际最大值。
三、问题3的模型建立与求解
1.压缩生产成本:引入优先因子,建立类目标规划模型
企业的生产成本可以认为由转运成本和仓储成本组成,即有如下表述:
第k周企业的生产成本Cpk由原材料转运成本Ct和原材料仓储成本Cwk组成,即
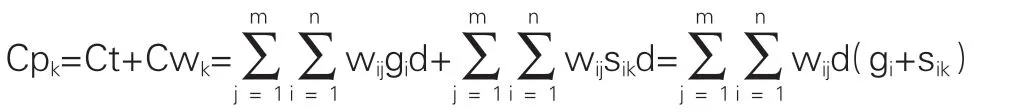
其中,d代表三类原材料运输和储存的单位费用。要能够取到minCpk,以实现压缩企业生产成本,即减少运输产生的转运成本和储存产生的仓储成本的目的。考虑到A、B、C三类原材料生产产品需消耗的原材料量(b1<b2<b3),即在满足生产需求且达到相当产能的条件下,考虑到订购量和相应供应量、接收量的强关联性,A、B、C三类原材料的订购量直接影响到企业的生产成本,容易知道尽量多地采购A类和尽量少地采购C原材料,可以达到压缩成本的目的。因而,对于新订购方案的制定,需要增加描述多选择A类原材料、少选择C类原材料的约束条件。我们通过对问题进行分析,发现只需要先尽可能地满足A类原材料的采购行为,再按照单位产品的原材料消耗量依次进行订购,就能够满足减少成本的需求。因此,在这里引入优先因子[3]ξj(j=1,2,i,m),为A、B、C类原材料的采购行为排定优先级的先后次序,将订购方案的类目标规划问题分解成一系列单目标规划问题依次进行求解。
综上所述,总的数学模型如下:
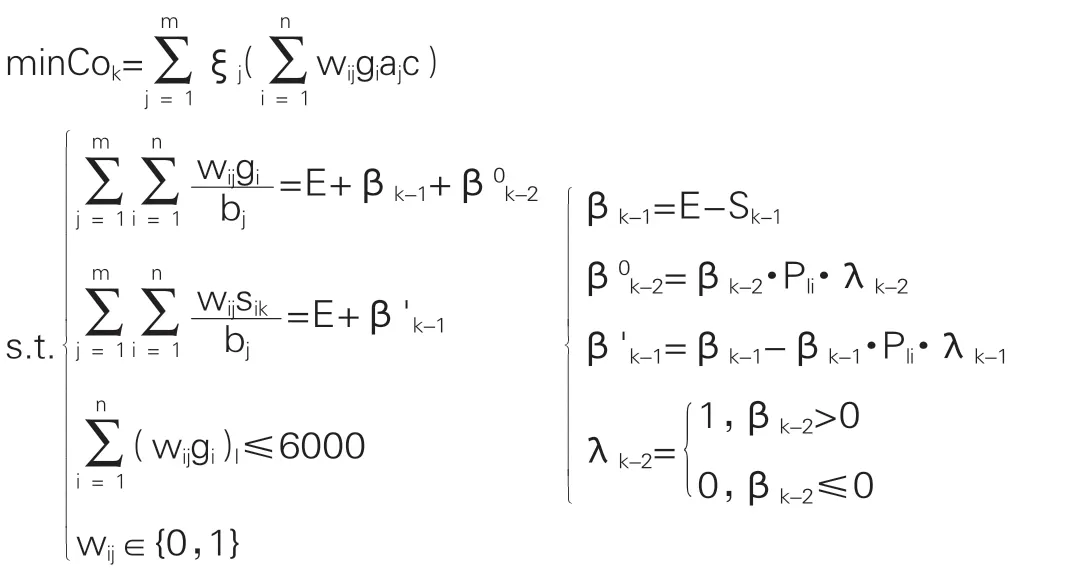
2.最少转运损耗率:建立优化模型
对于新转运方案的制定是在新订购方案确定出的供应商的基础上考虑转运商在运输原材料过程中的转运损耗率,转运损
耗率定义为总的转运损耗量与供应总量之比,其中,总的转运损耗量=供应总量-接收总量。第k周,转运商的转运损耗率应是转运损耗总量与总供应量之比,于是要求转运损耗率最低,即要求转运损耗总量Lk最低,因此可以继续沿用问题2中转运方案的数学模型,根据问题3中的采购方案给出如下数学模型:

3.模型求解
根据问题3,在尽可能多地采购A类原材料和尽可能少地采购C类原材料的约束下,建立新的订购方案和转运方案,通过编程求解。对应问题3中引入的优先因子,在程序求解时,具体实现方式为根据优先级的先后次序,将类目标规划问题分解成三类原材料下的单目标规划问题,然后再依次进行求解。
4.灵敏度分析
本问题中,在实际的订购和转运过程中,考虑到需求量Q和库存S对应的值与真实的值可能存在一定的偏差,至于不同种类材料的单位订购费用C、运输和存储费用是确切值,故不需要再做考虑[2]。采取对需求量Q和库存S做增加或减少10%大小的偏差处理,如图一所示:
5.实施效果分析
将订购量与实际供货量、供货量与实际接收量进行对比,可以分析方案自身的可行性与融洽性。

图1 灵敏度分析
订购方案:通过图2,可以看出订购量与实际供货量没有较大偏差,贴合度较好,说明制定的订购方案有效可行。
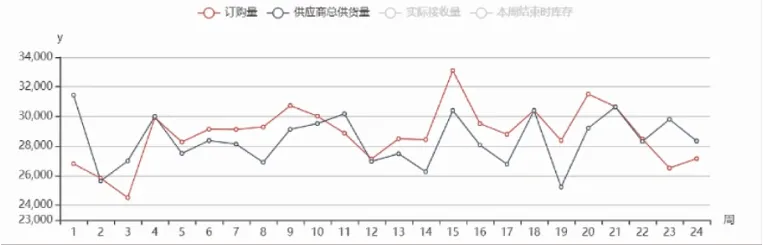
图2 订购量与供应商供货量对比
转运方案:通过图3,可以看出供应商供货量与仓库接收量几乎没有偏差,贴合度较高,说明制定的转运方案高效可行。
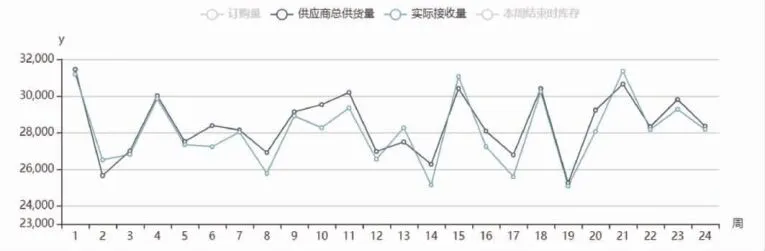
图3 供应商供货量与仓库接收量对比
四、问题4的基于二分法的产能潜力提高上限的求解
1.问题的进一步分析
问题4指出该企业具备了通过一定的技术改造方法提高产能的潜力,即此时企业的产能仅与现有原材料的供应商和转运商的实际情况有关,具体来说,就是企业产能的提高取决于供应商的供货能力(供货稳定性、最大供货量)和转运商的转运能力(运输能力、转运损耗率)。通过进一步的分析:一方面,可以发现存在隐性影响产能提高的因素,即单位产品产出所需的原材料消耗量b1,b2,b3,在本题中,这一隐性因素可以归结为原材料的类型。这也表示最大产能的提高也取决于原材料类型的选取上。另一方面,通过计算比较供应商的最大供货量与转运商运输的货物量上限,可以得到供应商最大供货量Ni>转运商运输货物量上限(6000m3>周)。继续深入分析,可以得出结论:在本题中,企业产能的提高上限决定于转运商全部转运A类原材料时所产生的成品数量。
2.求解方法
该企业原来每周的产能为E=28200m3(这里记为E0),假设提高后的产能为Et,产能提高上限为Em,则有Et∈[E0,Em]。
利用二分法原理求解产能最大值的过程:取E0和Em的中点值Et1,通过改变原有模型中产能E的参数值,变为Et1,依此得出能够满足条件的订购方案;再取E0和Et1,或是Et1和Em的中点值Et2,继续改变原有模型中的产能参数为Et2,得出能够满足条件的订购方案……照此进行下去,直到找到不能满足条件的订购方案的模型产能参数值Et(n+1),则可以得到产能最大值Etn,如上图4所示,同时,输出此种情况下的订购方案和转运方案,计算结束。
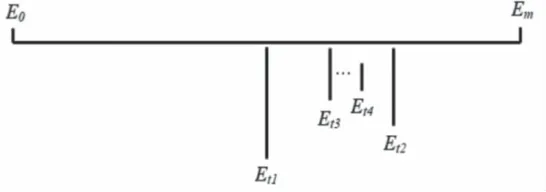
图4 二分法选取原理
3.求解结果
根据二分法原理,编程求解得出Etn=38200,得到此种情况下未来24周的订购方案和转运方案。
五、结束语
本文针对原材料选取问题,从前几年企业对供货商的需求度、供货商的供应稳定性、最大能供给量做出综合分析,并对处理结果进行稳定性分析等操作,最终得到未来24周的转运方案,根据以往数据和二分法预测出企业的最大产能上限,结合前面的问题求解方法给出未来24周的转运方案。
引用出处
[1]2021年全国大学生数学建模竞赛题[EB/OL].[2021-09-09].http://www.mcm.edu.cn/html_cn/node/4d73a36cc88b35bd4883c276afe39d89.html.
[2]蔡亚轩,郑志雯.木材加工企业的物流运输成本可控性研究[J].林产工业,2021,58(07):95-97.DOI:10.19531/j.issn1001-5299.202107020.
[3]卢方利,孙德宝.一类物资多目标规划的算法研究和评价模型[J].华中科技大学学报:自然科学版,2001,29(9):3.
[4]殷太平.二分法在调整中的应用[J].微电子学与计算机,1988(1).
