多中心协同模式下动态的车辆路径优化研究

文/柘佳怡

1.引言

随着共享经济的兴起，作为物流配送优化系统中的关键环节，多中心协同的车辆路径优化问题（Collaboration Multi-depots vehicle routing problem CMVRP）受到了广泛关注。传统的车辆路径（VRP）问题中，在优化之前，客户的地理位置、货物需求、时间窗等配送信息都是已知的，且是相对稳定的，不随着时间的推移产生变化，然后根据这些已知信息为配送中心的车辆进行路径优化，这类问题统称为静态车辆路径问题（Static SVRP），本文研究的多中心协同模式下车辆的动态路径问题（Collaboration Multi-depots vehicle routing problem with dynamic demands CMDVRPDD）在传统的VRP基础点行，同时考虑了多个配送中心之间的合作和车辆的动态路径优化，更加具有现实意义。

围绕着具有动态需求客户的配送网络和多中心的车辆调度问题，国内外的学者展开了一系列研究。在多中心协作配送方面，Wang等[1]提出了一种基于改进的粒子群算法研究了考虑同时取货和送货的共同配送问题。文军[2]研究了基于车辆共享的多配送中心车辆路径问题，并应用2-opt局部优化算法的自适应多态蚁群算法求解模型。范厚明[3]设计了一种变邻域搜索算法研究了多中心联合配送模式下集货需求随机的同时配集车辆路径问题。杨翔[4]运用两阶段禁忌搜索算法研究了多中心开放式模糊需求下的车辆路径问题。张婷等[5]研究了四种动态事件下的配送线路实时优化问题，利用混合遗传算法寻优。张文博等[6]研究了带时间窗的动态车辆路径问题，同时考虑了配送成本最小化和服务准时性最大化。Michal Okulewicz等[7]提出并分析了一种求解动态车辆路径问题的两阶段多群粒子群优化算法。

综上所述，学者们对多中心联合配送以及DVRP研究较为丰富，但上述文献在将多中心协同和动态车辆路径优化的结合上还有待深入研究。本文研究了基于多中心协同模式下车辆的动态路径规划，将配送中心的工作时间划分为多个周期，从而将DVRP转化为一系列SVRP。首先建立以最小化物流总成本和最小化车辆数为目标建立了双目标优化模型，其次，基于经典的SVRP模型，建立了初始优化阶段和动态调整阶段的两阶段优化模型，然后设计了一种改进的NSGA-Ⅱ算法进行求解，最后通过算例验证文章模型和算法的有效性。

2.问题描述

2.1 问题描述。针对动态车辆路径问题，采用多周期优化的策略将配送中心的工作时间划分为多个周期，将本周期出现的动态客户转移到下一时间段进行延迟处理，从而将DVRP转换为多个周期的SVRPs[8-9]，在单个周期内采用插入法将动态客户点插入原有路径中。因此，多中心协同模式下动态的车辆路径问题可描述为：配送中心先根据已知客户进行初始路径规划，在配送过程中根据客户需求的改变，以总成本和车辆数最小为目标，对路径进行动态调整。

2.2 问题分析及符号说明。假设配送中心D有l辆配送车辆，最大载重量为Q，对初始客户C1以及动态客户C2进行服务，配送中心和客户的时间窗分别是[ETd，LTd]和[ETc，LTc]，违反时间窗的系数为pe和pl，每公里的车辆油耗为fv，汽油价格为AV，车辆的固定成本为Mv，客户的需求量为qc。所有客户点的集合为C，配送中心和客户的集合为I，车辆到达配送中心和客户的时间为ATig，正在进行配送任务的车辆集合为H，车辆剩余的货物量为Qh，已经行驶的距离为Lh，任意两节点之间的距离为dij，DTij是车辆从节点i到达节点j的时间，任意两节点的行驶时间TTij，车辆在客户点的等待时间为WTcg，|Nig|是车辆g所行驶路径中客户点数量。当动态时间发生时，对未被服务的客户点重新编号C3，将正在执行配送任务的车辆v作为需求量为Q-Qh的虚拟的客户，且在配送途中的车辆必须先服务其对应的虚拟客户，对虚拟客户重新编号，虚拟客户和未服务客户的集合为C4。

3.两阶段优化模型构建

3.1 初始优化阶段。在初始优化阶段时，配送中心已知客户的配送信息，包括客户的货物需求量、时间窗、地理位置等。配送中心根据客户的信息生成一个初始的车辆路径方案，并按照该方案安排车辆执行，等到动态事件发生时，再对车辆路径进行动态调整。目标函数与约束条件如下：。

公式和是目标函数，公式表示初始阶段物流总成本最小化，公式表示使用的车辆数最小，公式表示车辆的配送成本和固定成本，公式表示惩罚成本，约束保证客户需求总量不能超过车辆的最大装载量，约束规定每个客户只能由一辆配送服务，约束表示流量守恒，约束用于消除子回路，约束和保证车辆到达客户和配送中心的时间必须在其时间窗内。约束和是车辆的到达时间，其中G为一个足够大的正数，约束表示决策变量，如果车辆g直接从节点i到节点j，则xijg=0，否则为0。

3.2 动态调整阶段。本文的动态调整采取周期性优化策略，将配送中心工作时间分为多个时间片，再某个时间片内发生的动态事件不会立即处理，而是转移至下一时间片与已规划路径中尚未服务的客户一同进行优化。将正在执行任务的车辆看成虚拟客户，将问题转化为静态的VRP。设动态客户的出现时刻为Tc，新增客户和原来未服务客户重新编号构成集合C3，剩余的货物量为Q-Qh。动态调整阶段的目标函数及约束如下：

约束保证虚拟客户首先被服务，约束规定每个客户只能由一辆配送服务，约束表示流量守恒，约束用于消除子回路，约束(20)和(21)保证车辆到达客户和配送中心的时间必须在其时间窗内。约束和是车辆的到达时间，，约束表示动态客户出现时时间必须在配送中心的时间窗内，约束表示决策变量，如果车辆g是初始阶段派遣过的车辆，则yg=1，否则为0。

4.两阶段算法设计及实现

4.1 k-means聚类。为了简化优化过程，得到更好的优化结果，利用k-means聚类方法根据客户的地理位置计算客户点之间的距离，根据计算结果将每个客户分配给邻近的配送中心。具体步骤如下：第一步：输入每个配送中心和客户的位置坐标；第二步：令k等于配送中心的数量，选择配送中心作为k个初始聚类中心；第三步：计算客户点到聚类中心的距离；第四步：将客户点分配给最近的聚类中心，如果客户点到达多个聚类中心的距离相等，则任意分配给某一聚类中心；第五步：计算每个聚类的均值作为新的聚类中心；第六步：重复以上步骤直到聚类中心不发生改变；第七步：输出聚类结果。

4.2 NSGA-Ⅱ算法。在初始优化阶段，采用改进的NSGA-Ⅱ算法规划配送路径，求得初始配送方案，当动态时间发生时，将动态信息转移到下一时间段，整合已规划路径中尚未服务的客户和动态客户，对路线进行动态调整，具体的步骤如下：第一步：设置算法相关参数;第二步：应用扫描法生成初始种群；第三步：计算适应度值；第四步：选择操作，结合精英保留策略和轮盘赌策略，对所有染色体的适应度进行排序，选择合适数量的适应度好的个体进行保留，保证子代的个体最优优于父代的个体最优，其余的个体采用轮盘赌的，策略进行选择；第五步：交叉操作，根据交叉概率选择染色体进行交叉运算，采用单点交叉法，两点交叉法和部分映射交叉法生成子代染色体[10]；第六步：变异操作，根据变异概率随机选择染色体进行变异操作；第七步：将初始种群和子代种群合并成新的种群，评价目标函数值，进行非支配排序并计算拥挤距离；第八步：进行迭代；第九步：通过排序选取帕累托优化解并输出最优解。

5.实例验证及分析

本文选取重庆市某物流企业的配送网络进行实例研究，选取4个配送中心，30个静态客户，20个动态客户，计算结果见表1。

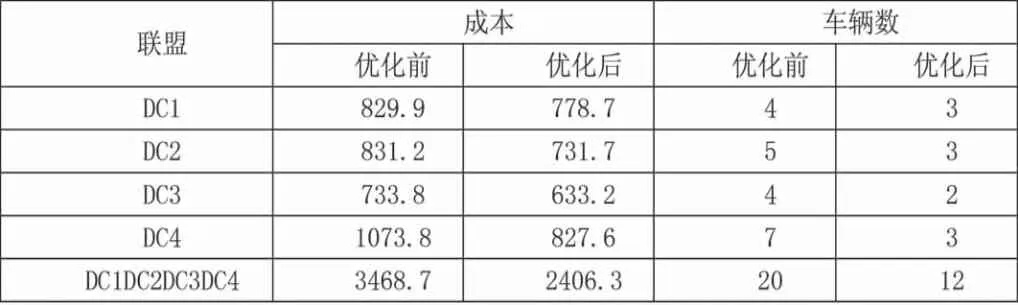
表1 计算结果

由表1计算结果可得，在各个配送中心独立运行的情况下，通过初始阶段预优化，再根据动态事件对车辆路径进行动态调整的两阶段优化策略，车辆数和成本都有一定程度下降。在考虑各个配送中心协作模式的情况下，成本下降了30.6%，车辆数由20辆减少到了12辆，减少了8辆。显而易见，配送中心之间相互协作形成大联盟，将单个配送中心独立配送模式转换为共同配送的配送模式能够有效地降低物流网络的运营成本。

6.结论

本文基于多中心协同模式下动态的车辆路径优化问题，首先，针对动态事件的发生，将DVRP转化为连续的SVRPs。其次，建立了以总成本和车辆数为目标的双目标两阶段模型。然后，将k-means聚类和改进的NSGA-Ⅱ算法结合，降低了算法的复杂性，提高了算法的全局搜索和局部搜索能力。最后，在现实生活中选取实例研究模型和算法的有效性，计算结果表明，多中心协作配送的模式能够有效降低物流成本，提高车辆利用率。

引用出处

[1]Wang,Y.,Li,Q.,Guan,X.Y.,Fan,J.X.,Liu,Y.,Wang,H.Collaboration and Resource Sharing in the Multidepot Multiperiod Vehicle Routing Problem with Pickupsand Deliveries[J].Sustainability.2020,12(15):5966.

[2]文军.基于车辆共享的多配送中心车辆路径问题研究[J].物流工程与管理[J],2019,41(02):75-77+72.

[3]范厚明,刘鹏程,刘浩,侯登凯.多中心联合配送模式下集货需求随机的VRPSDP问题[J/OL].自动化学报:1-15[2021-05-07].http://202.202.244.12:80/rwt/CNKI/https/MSYXTLUQPJUB/10.16383/j.aas.c190519.

[4]杨翔.多中心开放式VRP拓展问题建模及算法研究[D].大连海事大学,2019.

[5]张婷,赖平仲,何琴飞,靳志宏.基于实时信息的城市配送车辆动态路径优化[J].系统工程,2015,33(07):58-64.

[6]张文博,苏秦,程光路.基于动态需求的带时间窗的车辆路径问题[J].工业工程与管理,2016,21(06):68-74.