基于粒子群算法的农产品物流车辆路径问题

文/朱利

引言

由于生鲜农产品具有易腐和易损的特殊性，为了保证农产品的品质以及新鲜度，减少农产品的变质损坏率，需要将农产品快速送到客户手中，这使得在农产品物流车辆路径问题中对运输时间、运输距离的要求非常高。Dantzig和Ramser[1]1959年首次提出车辆路径问题（VRP），研究了如何调度配送车辆使得车辆行驶的总距离最短。Clarke和Wright[2]将车辆调度问题推广到物流运输中的优化问题.随着研究的不断深入，衍生了带时间窗的车辆路径问题（VRPTW）的研究，Solmon[3]在1986年对VRPTW 进行了问题描述，构建了该问题的数学模型并完成了问题求解。VRPTW 在实际问题中表示每个客户都有一定的接受服务的时间要求，车辆服务此客户在其要求的时间范围内，否则客户不接受服务或会产生一定的时间（惩罚）成本[4]。本文在农产品物流车辆路径问题研究中，考虑客户服务时间窗，构建了物流配送总成本最小化的优化模型，并运用粒子群算法求解该模型，最后通过实例验证了模型和算法的有效性，对农产品物流车辆路径优化提供了参考和决策支持。

1.问题描述

农产品对物流的时效性有着严苛的要求，带时间窗的农产品物流车辆路径问题可以描述为：K辆农产品物流配送车辆从同一配送中心出发，对属于配送范围的客户需求点进行配送，在满足客户需求及服务时间窗的前提下，考虑农产品物流配送车辆的容量限制，以农产品物流配送总成本（配送车辆的租赁成本、配送成本、违反时间窗惩罚成本）最小化为目标，对农产品物流配送车辆路径优化，进而降低农产品物流配送成本。

2.模型构建

2.1 符号说明

I={i｜i=1，2，3，…，n}表示客户点集合；I0表示配送中心和客户点集合；K={k|k=1，2，3，…，v}表示农产品物流配送车辆集合；Nk表示农产品物流配送车辆k服务客户点集合；|Nk|表示农产品物流配送车辆k服务客户的数量；Qk表示农产品物流配送车辆最大装载量；qi表示客户i的需求量，且qi≤Qk；[ei，li]表示客户i的服务时间窗；atik表示农产品物流配送车辆k到达节点i的时间；dtik表示农产品物流配送车辆k离开节点i的时间；ttik表示农产品物流配送车辆从客户i到客户j的行驶时间；α 表示农产品物流配送车辆早到的单位时间惩罚系数，β 表示表示农产品物流配送车辆晚到的单位时间惩罚系数；dij表示客户i到j的配送距离；ck表示农产品物流配送车辆k单位距离行驶成本；δk表示农产品物流配送车辆的租赁成本；NN表示一个足够大的正数。xijk为0-1变量，如果农产品物流配送车辆k从客户i行驶到客户j时等于1，否则等于0；yik为0-1变量，如果客户由农产品物流配送车辆服务是等于1，否则等于0。

2.2 数学模型

本文以总配送成本最小为优化目标，其中，包括配送车辆的租赁成本、配送成本和违反时间窗惩罚成本。农产品物流配送优化模型如下：minZ=TC+FC+PC

TC：农产品物流配送车辆将农产品送达客户的配送成本

FC：农产品物流配送车辆的租赁成本

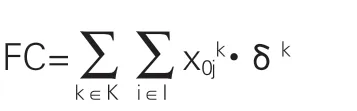
PC：农产品物流配送车辆违反客户服务时间窗的惩罚成本

式（1）表示每个客户只能被一辆农产品物流配送车服务；式（2）表示农产品物流配送车辆将农产品送达客户后必须离开；式（3）表示消除农产品物流配送线路上的子回路约束；式（4）表示产品物流配送车辆的容量约束；式（5）和式（6）农产品物流配送车辆到达客户的时间；式（7）和式（8）表示农产品物流配送车辆离开和到达配送中心的时间在配送中心的服务时间窗内；式（9）和式（10）表示变量约束。

3.粒子群算法

粒子群优化算法是由Kennedy和Eberhart[5]在1995年提出的一种基于群体智能优化算法，实质是模仿鸟群觅食的行为，通过个体间的协作与竞争来搜索最优解。粒子群算法将每个粒子的行为规则设定为类似鸟类运动的简单的行为规则，从而是粒子群的运动表现出与鸟类迷失行为相类似的特性，每一个个体将自身所学习到的知识或经验与种群中其他的个体共享，同时也获得其他个体的经验，并基于这些信息不断地调整自己的行为模式。粒子群算法的思路是将研究问题的解空间作为鸟群的飞行空间，根据问题的不同约束条件，限制解空间的范围，解空间的每一个点都代表问题的一个可行解，食物则是接空降中最优解的位置。每个粒子都有决定飞行方向和距离的速度，粒子根据自身的飞行经验以及同伴的飞行经验来调整飞行，用适应值来评价粒子当前位置的好坏。整个优化的过程与鸟群在整个解空间中寻找食物的过程类似，粒子们追寻当前的最优粒子在解空间中搜寻。每个粒子都具有记忆个体历史最优位置的能力，且粒子与粒子之间的信息能够共享，这样就可以实现种群中每一个个体的自我学习和相互学习，利用个体最优信息和种群最优信息进行种群的迭代来实现问题的优化求解。

3.1 相关变量定义及公式

相关的定义和符号定义如下：

np：粒子群优化过程中使用的粒子数。

c1和：c2粒子群算法中使用的加速系数。

w1和：w2粒子群算法中使用的惯性因子。

pbesth（t）：粒子群优化算法中迭代次数为t的粒子h的个体最佳位置。

gbesth（t）：粒子群优化算法中迭代次数为t的粒子h的个体最佳位置。

完成配送服务的粒子群的速度和位置更新的公式如下：

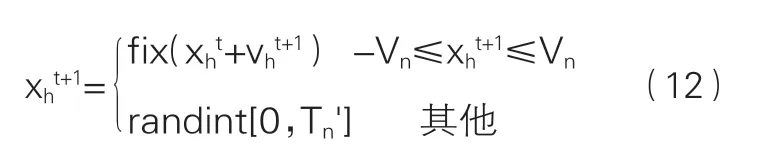
其中，c1和：c2是两个加速度，rand（t）表示介于0到1之间的随机数，fix（t）表示每个粒子的位置是一个整数，Vn表示配送服务允许的最大速度，randint[0，Tn']表示0或Tn'的整数，其中Tn'表示配送服务所需物流设施的数量。

3.2 步骤及实现过程

Step1：算法初始化。在[0，Tn']内随机生成粒子的位置矢量，在[-Vn，Vn]内随机生成粒子的速度矢量，并设置迭代次数run=1；

Step2：计算粒子适应度值，并找到个体最优pbesth（t）和全局最优gbesth（t）；

Step3：按式（9）和式（10）更新粒子的速度和位置

Step4：计算粒子适应度值

Step5：对所有粒子，若其当前适应度优于其历史最优适应度，则将当前位置设置为该粒子的历史最优位置，然后更新全局最优。

Step6：如果达到最大迭代次数run_max，则循环完成；否则，返回Step3。

4.算例分析

4.1 算例相关数据

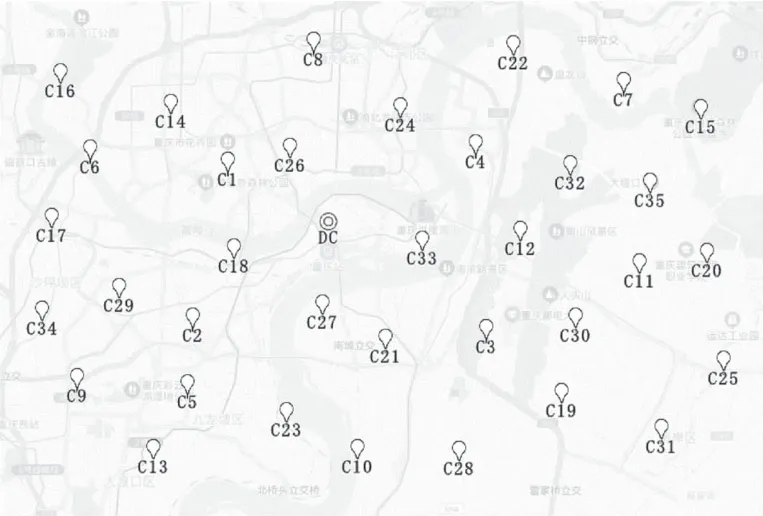
为验证模型与算法的有效性，以重庆市某农产品物流配送中心（DC）及其服务的35个客户点（C1-C50）为例进行研究，相应的地理位置分布如图所示。根据已有相关文献[6，7]和实例数据规模，设置相应参数为：Qk=200，δk=100，ck=3，α=10，β=25，np=100，run_max=，c1=c2=2。

4.2 结果与分析

运用粒子群算法求解农产品物流配送车辆路径优化问题，得到农产品物流配送车辆优化方案：农产品物流配送车辆1的配送路线为DC→C33→C3→C19→C25→C31→C28→DC，农产品物流配送车辆2的配送路线为DC→C1→C17→C34→C29→C2→DC，农产品物流配送车辆3的配送路线为DC→C27→C5→C9→C13→C23→C10→C21→DC，农产品物流配送车辆4的配送路线为DC→C12→C30→C11→C20→C15→C7→DC，农产品物流配送车辆5的配送路线为DC→C26→C14→C16→C6→C18→DC，农产品物流配送车辆6的配送路线为DC→C35→C32→C4→C22→C24→C8→DC。农产品物流配送车辆路径优化前，车辆使用数为8，车辆租赁成本为800元，配送成本为2258元，违反时间窗惩罚成本为254元，物流配送总成本为3312元。农产品物流配送车辆路径优化后，车辆使用数为6，车辆租赁成本为600元，配送成本为1463元，违反时间窗惩罚成本为28元，物流配送总成本为2091元。应用粒子群算法优化后的农产品物流配送方案相比优化前的配送方案，农产品物流配送车辆使用数节省了25%，农产品物流配送车辆租赁成本节省了25%，违反时间窗惩罚成本减少了88.98%，农产品物流配送成本减少了35.21%，农产品物流配送总成本节约了36.87%。

5.结论

本文研究了带时间窗的农产品物流车辆路径优化问题，考虑农产品物流配送车辆的容量限制和客户不同的服务时间窗进行合理的农产品物流配送路线优化，建立了包含农产品物流配送车辆的租赁成本、配送成本和违反时间窗惩罚成本的农产品物流配送总成本最小化的目标优化模型，并运用粒子群算法求解该模型，最后结合重庆市某农产品物流配送中心的实际配送数据，通过求解该模型，进一步验证所提模型与算法的可行性。计算结果表明，相对于农产品物流配送车辆路径优化前，优化后的农产品物流配送车辆路径优化方案的物流配送总成本和车辆使用数分别减少了35.21%和25%，违反时间窗惩罚成本降低了88.98%。研究结果表明对农产品物流配送车辆进行合理的路径优化，能减少农产品配送的运输距离和运输时间，降低农产品配送的物流总成本。

引用出处

[1]Dantzig G B,Ramser JH.The truck dispatching problem［J］.Management Science,1959,6(1):80-91

[2]Clarke G,Wright JW.Scheduling of Vehiclesfrom a Central Depot to a Number of Delivery Points[J].Operations Research,1964,12(4):568-581.

[3]Solmon MM.Algorithm for the Vehicle Routing Scheduling Problemswith Time Window Constraints[J].Operations Research,1987,35(2):254-256.

[4]庞燕,罗华丽,邢立宁等.车辆路径优化问题及求解方法研究综述[J].控制理论与应用,2019,36(10):1573-1584.

[5]Kennedy J,Eberhart R.Particle swarm optimization[C]//IEEEInternational Conference on Neural Networks.Piscataway,USA,IEEE,1995:1942-1948.

[6]Li J,Li Y,Pardalos PM.Multi-depot vehicle routing problem with time windowsunder shared depot resources[J].Journal of Combinatorial Optimization,2016,31(2):515-532.

[7]Veenstra M,Roodbergen K J,Coelho L C,Zhu SJ.A simultaneous facility location and vehicle routing problem arising in health care logistics in the Netherlands[J].European Journal of Operational Research,2018,268(2):703-715.