自适应编码与混合模型联合改进图像压缩算法
2023-02-09李耀莹
李耀莹,孙 娟
(1.山西师范大学临汾学院,山西临汾 041000;2.临汾市人民医院,山西临汾 041000)
1 引言
图像中的相邻像素点存在冗余,即相邻像素点存在高度相关性,因而图像像素值可由其邻近值进行合理预测[1−2]。从实际像素值减去预测像素值就获得了残差图像,可对残差符号以及特定的统计模型进行编码。只要概率模型接近于真实模型,编码过程就会获得较好的压缩效率,统计估计模型越精确,压缩效率就越接近最佳值[3−4]。
显然,对于图像压缩而言,尤其是在图像中符号分布随着位置的变化而变化的时候,现有的统计模型无法解决建模的问题。为引,研究人员展开图像统计建模的研究,文献[5]使用双边几何分布对图像/视频编码算法中的残差分布进行建模。文献[6]提出了零均值拉普拉斯分布对每个错误像素点的概率进行估计;文献[7]根据上下文建模对预测误差的概率密度函数进行了分类,然后利用广义高斯函数对其进行建模。文献[8]提出利用不对称双边几何分布对预测误差进行建模。文献[9]提出了一种基于算术编码(Arithmetic Coding,AC)的改进无损图像压缩方案,混合使用了若干非参数分布。在已有研究基础上,提出了一种基于自适应算术编码以及几何分布有限混合模型的分块无损图像压缩算法。
算法首先对预测残差图像进行编码,然后将该残差图像分成若干非重叠块,并通过混合几何分布估计各个分块的统计模型,然后通过最大似然估计(Maximum Likelihood Estimation,MLE)估计混合参数,最后在预测误差块中使用直方图截断算法进一步减少算术编码中的符号数量,从而减少零次符号的出现概率,实验结果验证了算法的有效性。
2 改进图像压缩算法
由于邻近像素点之间的空间相关性降低,基于自适应无损图像编码[10]的梯度预测器或者JPEG−LS[11]的中值边缘检测器(Me‐dian Edge Detector,MED)等预测技术有助于获得较好的压缩性能。但是,在某些情况下,基于几何分布或者拉普拉斯分布的简单统计建模无法提供准确的残差图像概率分布。为此,将集中研究明确基于混合模型的压缩方法,以便对残差图像块的概率密度函数(Probability Density Functions,PDF)进行有效估计。这里提出方法的流程框图,如图1所示。在下面部分中,对编码过程中的各种步骤进行了介绍。

图1 改进图像压缩算法的流程框图Fig.1 Block Diagram of the Proposed Improved Image Compression Algorithm
2.1 误差预测以及映射
由编码像素值可获得当前像素x的预测值x,为此,不失一般性,选择MED作为预测器。MED使用的是x因果邻域中的三个像素点,根据式(1)检测图像的水平边缘和垂直边缘。
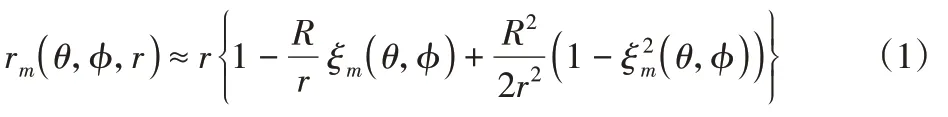
从待编码的当前值中减去预测值就能够获得预测残差e,即:e=x−。8位灰度图像的残差符号范围为[−255,255]。因此,应将统计模型用于算术编码,该统计模型带有511 个符号的字母集。需注意,范围较大也就意味着需要较多位表示预测误差。所以,在对其进行编码之前使用了下列误差映射:

在这种情况下,符号范围缩减至[−128,127];因此,符号数量变成了256,从而进一步提升了AC的编码增益。
文中将几何有限混合模型用于统计数据建模。因此,预测误差必须映射到非负值,如下所示:

式中:e-映射图像,默认的误差字母范围为[0,255]。
2.2 映射图像划分
由于编码后序列的每个符号熵是长度的递减函数,将映射图像分成N个非重叠块,则在字母A范围内将数据集X分成N个非重叠子集会使平均熵衰减,因而有:
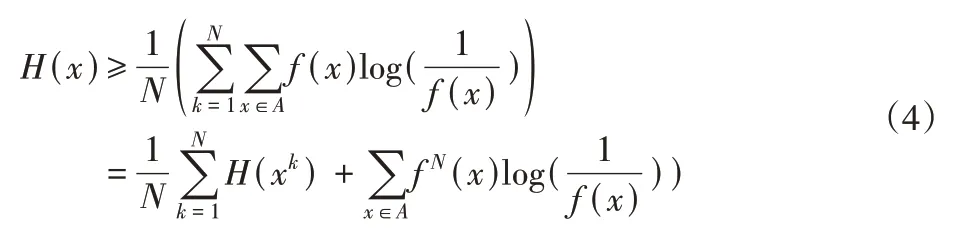
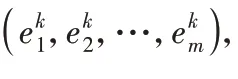
2.3 几何有限混合模型建模
有限混合模型(Finite Mixture Models,FMM)[12]提供了强大且灵活的概率模型,已成功地用于密度估计、聚类以及分类等领域。分布f是根据下列公式进行地混合K分量分布:



利用迭代EM算法[3]并通过MLE能够有效地对FMM参数进行估计。首先,EM算法对混合参数ψ进行初始预测,然后通过反复采取下列两个步骤寻找MLE:
(1)计算后验概率:在进行第t次迭代时,通过第j个混合分量的观测值xi,得到第i个样本成员。
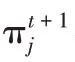

如果使用混合几何分布,实际映射块E的PDF估计包含个符号,表示为:
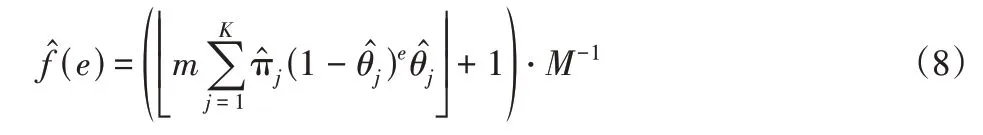
式中:e∈B。在实验过程中发现,当图像像素点之间的相关性并不明显时,用于映射块的几何分布FMM与真实统计数据存在不匹配情况,从而使映射块的概率分布在整个字母范围内失真。为此,文中提出采用基于模型切换器的对数似然比(Log−Likelihood Ratio,LLR)测试,通过LLR测试,由该切换器决定是在均匀模式下还是混合模式下进行建模。

式中:-真实频率计数向量,用于表示块E的位数接近于−log2(L(E,))。设UB为字母集B中的离散均匀分布,其符号具有相等的概率 |B|−1。编码之后分别通过UB以及更新映射误差频率计数对每个映射块进行编码,似然函数为:

3 实验分析
为验证文中提出的改进图像压缩算法的压缩性能,采用图像集作为实验数据进行实验,如图2所示。图2中六幅测试图像分别为man、boat、airplaneU2、Lena、dollar、testpat。

图2 实验用原始测试图像Fig.2 The Second Set of Three Original Test Images
3.1 对数似然比测试结果
幅图像“lena”的所有映射块的两个几何模型与均匀模型之间的LLR,如图3所示。从图3(a)可看出,混合模型更符合图像中大多数映射块的统计数据。
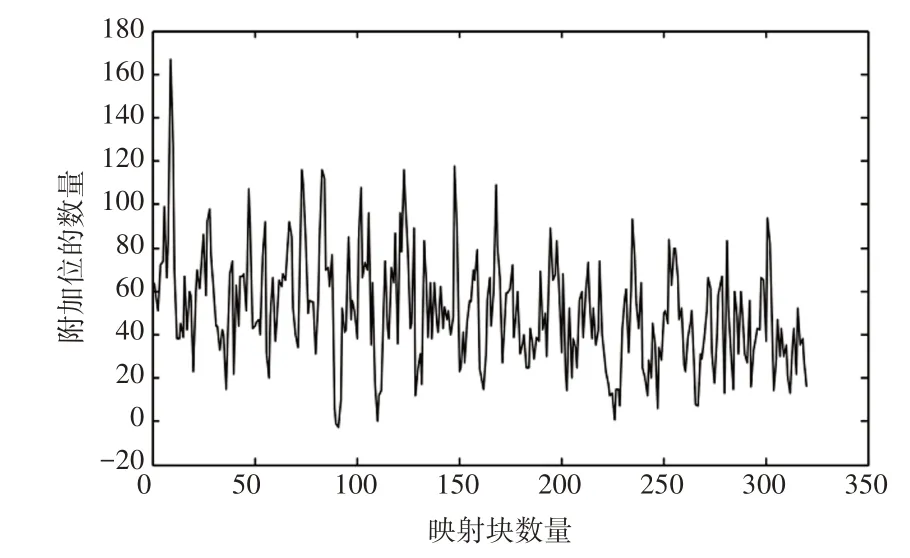
图3 “lena”图像几何模型与均匀模型之间的LLRFig.3 LLR Between Image Geometry Model and Uniform Model
3.2 压缩比结果
在实验分析过程中,采用文中方法根据压缩比对编码性能进行了测量,结合MED预测器并通过单个分布以及两个混合几何分布得出的第一个图像集的压缩比,如表1所示。可以看出,图像集通过两个混合几何分布对每个尺寸为32×32的映射块进行编码,获得的平均压缩比分别为2.58。

表1 第一组图像的块编码压缩比Tab.1 Encoding Compression Ratio of the Image Blocks
3.3 性能比较结果
为了深入分析这里提出的方法的性能,将这里提出的基于自适应编号与混合模型的图像压缩方法与两种已有文献中的图像压缩标准进行比较,多次实验结果的平均值,如表2所示。表中给出了先进的无损图像压缩标准以及文中混合模型得出的实验图像集的压缩比。
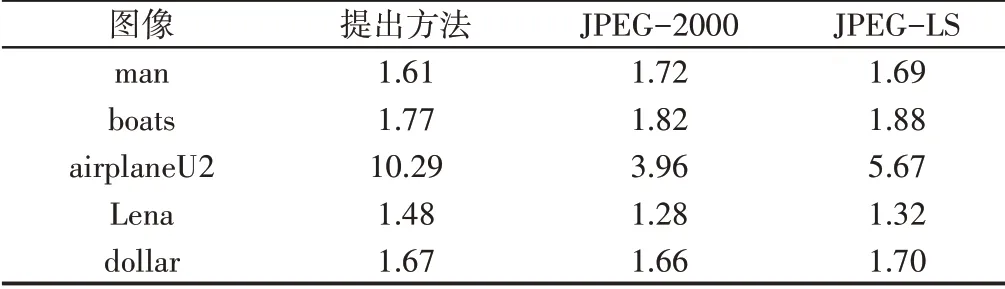
表2 第一组图像集的压缩比比较结果Tab.2 Compression Ratio of the First Image Sets
根据上述结果可知,对于第一个图像集而言,平均来说,利用文中提出的方法获得的压缩比JPEG−2000以及JPEG−LS高出了约55%和40%。从表3 可看出,第二个图像集的压缩比范围为(2.40~89.58);并且,平均来说,利用文中提出的方法获得的压缩比JPEG−2000以及JPEG−LS高出了约240%和85%,优于这两个先进标准。
4 结论
这里提出了一种用于基于无损AC 图像压缩方案的几何分布有限混合模型。相较于单个几何分布,文中提出的几何分布能够较好地建模。这里提出的方案合并了混合模型与均匀模型之间的对数似然比测试,以便确保更好地调节残差块的统计模型。此外,采用了直方图截断来解决零频率问题,从而确保使用均匀模型或者有限混合模型时统计失真情况减少。从实验结果中可看出,在上述两幅图像集的压缩比方面,文中提出的压缩方法优于先进标准JPEG−2000和JPEG−LS。
