轨迹插补加减速离散算法改进
2023-02-09游达章康亚伟
游达章,余 炼,张 敏,康亚伟
(湖北工业大学机械工程学院,湖北武汉 430068)
1 引言
步进或伺服电机被广泛应用于数控机床上,其加减速控制源于给定脉冲频率的改变。从微观层面看,电机转轴在单位脉冲周期内经历了加速再减速而后短暂延时的过程,可认为在该极短时间内电机是匀速转动的。因而,随着脉冲频率的改变,电机转速随时间变化呈“阶梯状”。因而刀具在进给过程中速度随电机不连续变化,该过程称为加减速离散过程。文献[1]研究步进运动控制系统最优插补周期的过程中提到了步进电机的理论运动平稳性指标,认为速度阶跃变量(即“台阶”高度差)越小,电机运行将越平稳,为评价速度变化的平稳性提供了指标。文献[2]提出的基于位移等效原则对时间连续速度曲线进行周期化离散变换的方法,为改进连续速度曲线周期化离散提供了良好的算法基础;文献[3]提出的加减速离散算法给出了速度迭代公式,可以避免处理预测减速点,但以上二者都并未着眼于减少迭代次数。传统离散算法每走一步,计算一次脉冲间隔时间(即插补周期),这样能使精度达到最高。而当加工路径起始点距离过长、加工精度要求不高时,没有必要每隔一步计算一次插补周期。为了减少计算量,并能够针对不同加工精度对“台阶”高度做出调整,使计算量和精度最合适,可以用每隔多步计算一次脉冲间隔时间的方法改进离散算法。仿真结果表明,改进的离散算法能够有效减少计算量,并能够较为真实地描述和还原速度和位移随时间的变化关系。
2 传统加减速离散算法原理
2.1 步进条件的定义
刀具沿着加工路径,从起点向终点进给,其速度随时间的变化关系为v(t),位移随时间的变化关系为S(t),如图1所示。为了实时跟踪位移量,需每经过一段很短时间计算一次位移。从起始点开始,若以下条件成立:

图1 传统加减速离散算法原理Fig.1 Principle of Traditional Acceleration/Deceleration Discrete Algorithm

式中:D—加工路径起点到终点距离/mm;N—加工路径起点到终点总步数/steps;λ—距步比;T—采样周期/min;xs,i—第i次满足步进条件时距离起点的实际步数,且xs,i=i;xt,i—第i次满足步进条件时离起点的理论步数;yi—第i次满足步进条件时离起点的理论距离。
每次满足步进条件向电机发送单位脉冲以驱动电机。
2.2 加减速离散算法实现过程
从起点开始,经过n1个采样周期T之后,首次满足步进条件,如图1所示。
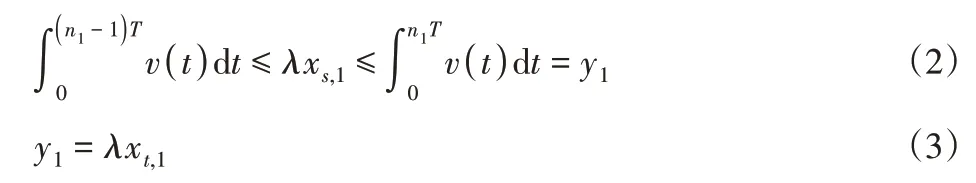
视在步数区间(0,xs,1]内刀具沿进给方向匀速运动,历时时间近似为t1,且:

那么,可近似得到该区间内速度的平均值:

事实上,在xs,1处的速度为v1,而在区间(xs,1,xt,1]内的速度理应大于v1,因而要将该区间多出的时间和位移“掐尾”。在区间(0,xs,1]所经历的时间。

那么,可近似得到该区间内速度的平均值:

则理论上认为在步数区间(xs,i−1,xt,i]内为匀速运动,且时间近似满足。

则该区间的速度近似满足:
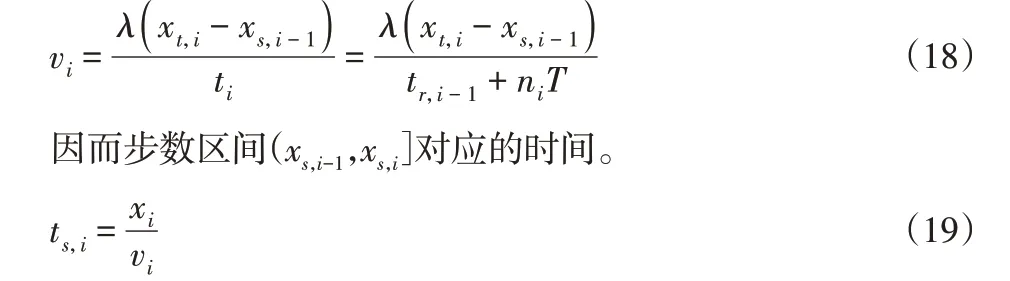
式中:xi—第i次满足步进条件时的前进步数。

多出的剩余时间tr,i计入下一个周期,其中:

由此得到速度随时间和步数的迭代公式:
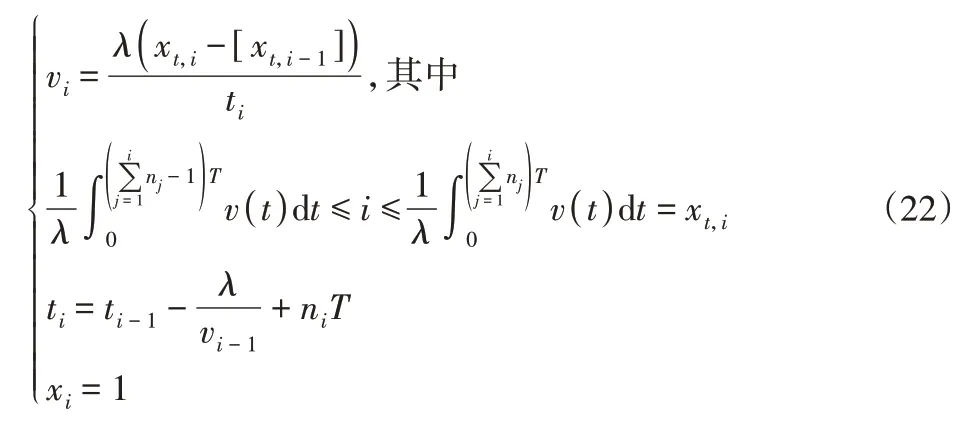
式中:vi—第i次插补平均速度;xi—第i次插补前进步数;ti—第i次插补历时时间。
其中,初始条件为:

3 加减速离散算法的改进
3.1 改进加减速离散算法原理
刀具沿着加工路径,从起点向终点进给,其速度随时间的变化关系为v(t),位移随时间的变化关系为S(t),如图2所示。
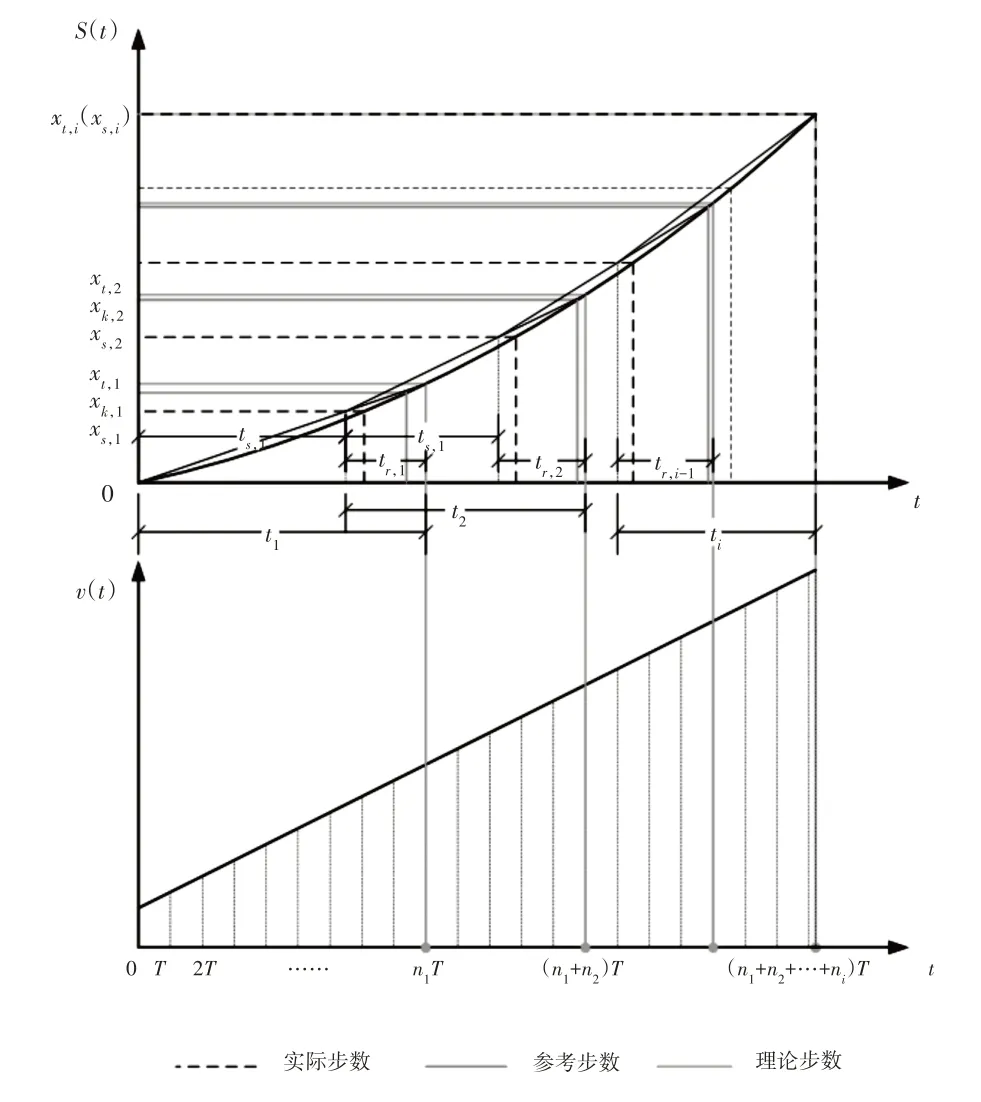
图2 改进加减速离散算法原理图Fig.2 Schematic Diagram of Improved Acceleration/Deceleration Discrete Algorithm
从起始点开始,若以下条件成立:

式中:D—加工路径起点到终点距离/mm;
N—加工路径起点到终点总步数/steps;
T—采样周期/min;λ—距步比;
xk,i—第i次满足步进条件时距离起点的参考步数,且xk,i=σi,σ≥1;
xt,i—第i次满足步进条件时离起点的理论步数;
yi—第i次满足步进条件时离起点的理论距离。
每次满足步进条件向电机发送若干脉冲以驱动电机。重复2.2中的推导过程,不难得知,当再次经过ni个采样周期T之后,得到速度随时间和步数的迭代公式。
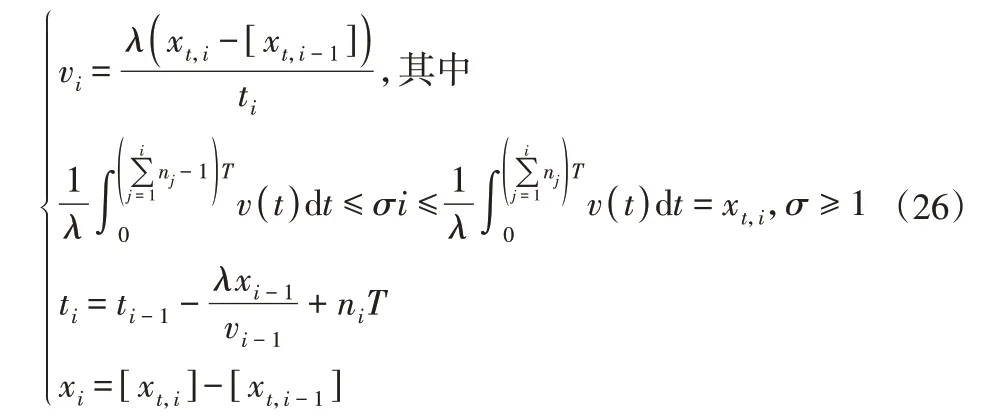
式中:vi—第i次插补平均速度;xi—第i次插补前进步数;ti—第i次插补历时时间。
其中初始条件为:

3.2 算法改进前后对比
将改进前和改进后的算法总结为流程图,如图3所示。可知算法改进前后的区别在于步进条件的不同。


图3 加减速算法改进前后流程图对比Fig.3 Comparison of Flowcharts Before and After the Acceleration/ Deceleration Algorithm is Improved
事实上,当σ=1时,改进后的加减速离散算法就是改进前的算法。
4 改进算法的应用和评估
4.1 改进算法的应用
假设某加工路径起始点的坐标为:(0,0),终点坐标为:(0.08mm,0.05mm),总步数为64,给定的速度为:50mm/min,加速度为:42453mm/min2,起点和终点速度为:0,采样时间为:1/1920000min。
那么可以得到速度和位移随时间的变化关系,如图4(a)、图4(b)所示。采用改进前的离散算法,得到速度随时间和步数的变化关系,如图5所示。
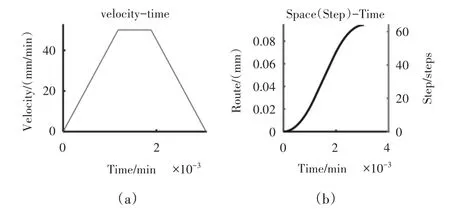
图4 速度和位移随时间的变化关系Fig.4 Relationship Between Speed and Displacement over Time

图5 速度随步数和时间的变化关系Fig.5 Relationship Between Speed and Number of Steps and Time
在不改变速度−时间关系的前提下,通过增大“台阶”高度差,得到改进之后的速度随时间和步数的变化关系,以σ=1.25,1.5,1.75为例,如图6所示。
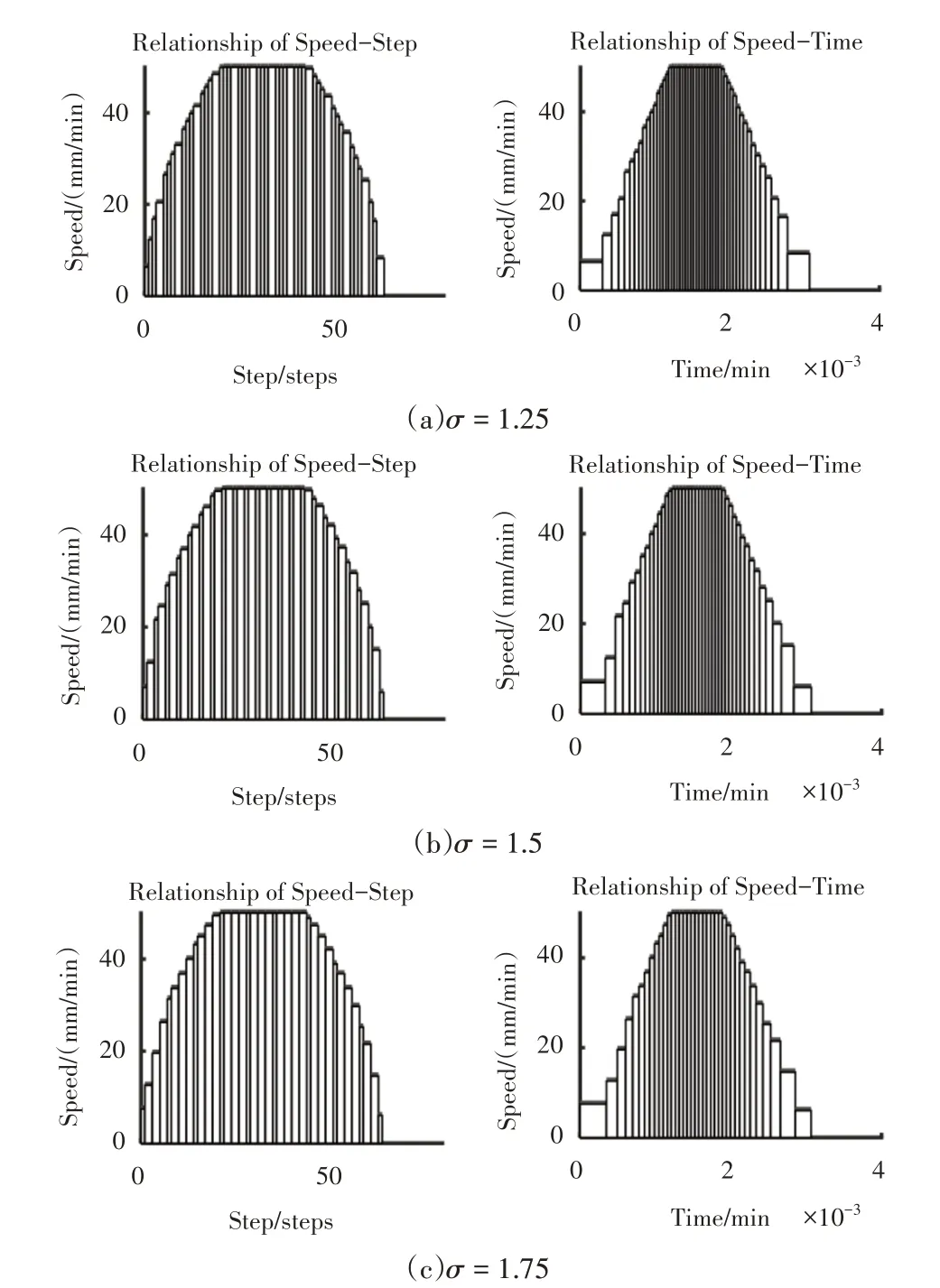
图6 σ对速度−步数和速度−时间关系的影响Fig.6 Effect of σ on Speed−Step Number and Speed−Time Relationship
位移−时间的变化关系,如图7所示。


图7 不同σ对位移−时间关系的影响Fig.7 Effect of Different σ on Displacement−Time Relationship
可知,将σ控制合适范围内,改进后的算法仍然能较好地还原位移—时间关系。
4.2 改进算法的评估
首先,为了更好地评价改进后的离散算法得到的速度−时间曲线对理论速度−时间曲线的拟合程度,引入评价指标:
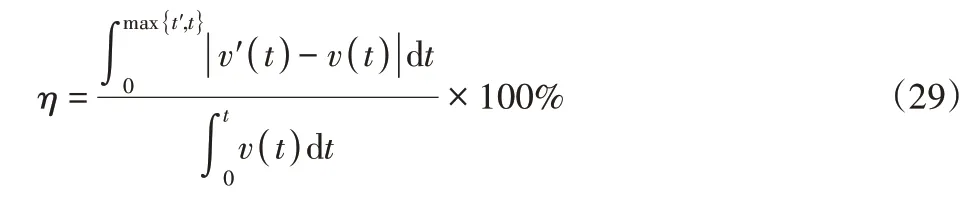
式中:v′(t)—改进离散算法得到的实际速度−时间函数;v(t)—理论速度−时间函数;t′—实际总时间;t—理论总时间;η—实际曲线对理论曲线的拟合度,无量量纲。
分子为该两条函数曲线围成的面积,分母为起点到终点位移。η值越小,表示拟合度越好。其次,不可否认,改进后的离散算法对平稳性有着重要影响,文献[1]中提到的速度跃变量可作为平稳性的衡量指标。

式中:v—加减速过程的速度变化量;K—速度跃变次数。
速度越变量越小,平稳性越好。最后,统计改进离散算法得到的迭代次数i,得到计算量的评价指标。通过改变σ的值,得到σ对以上3个指标的影响,如图8所示。

图8 σ对评价指标的影响Fig.8 Influence of σ on the Evaluation Index
从图8中可知,σ在取值在(1,3]时,改进离散算法得到的速度−时间曲线仍然能较好的拟合理论速度−时间曲线。
此外,迭代次数i也随σ增大而增大,当σ为3时,迭代次数减少了近2倍。但在一定程度上牺牲了平稳性,当σ为3时,速度阶跃变量增大了近1.8倍。总体来看,效率增长速度比平稳性下降速度要快。因而,对于加工路径过长,加工精度不高的时,可适当增大σ以减少迭代次数和计算量,提高加工效率。
5 结论
针对加工路径较长,精度要求不高的场合,为了减少计算量,并能够针对不同加工精度对“台阶”高度做出调整,使计算量和精度达到最优,可以每隔多步计算一次脉冲时间间隔。仿真结果表明,改进的离散算法能够显著减少迭代次数,并能够较为准确地描述和还原速度和位移随时间的变化关系。
