四旋翼飞行仿真器的PID神经元网络控制器设计
2023-02-09刘祚时徐燕生
刘祚时,陈 飞,徐燕生,曾 锋
(江西理工大学机电工程学院,江西赣州 341000)
1 引言
随着科技的快速发展,旋翼式飞行器也在不断发展。旋翼式飞行器因有着操作灵敏、控制稳定且应用广泛等优点,具有较高的应用潜力与研究价值。
控制器的实时性和精确性是旋翼式飞行器研究者不断追求的目标,其控制方法主要有PID控制、LQR控制、反步式控制等,但它们在一定程度上很难保证实时性和精确性的高度统一。其中,对于PID控制是最为简单,有效的控制方法,但在闭环系统中容易产生“快速性”和“超调”等问题,对PID控制进行优化也是常用方法。文献[1]提出了与辨识的模糊模型结合使用的PID 控制器,但在进行模糊C均值聚类时采集数据大,实时控制精确度不高。文献[2]采用改进的PSO 算法和遗传算法对PID 参数进行优化,但计算过程复杂、周期长,难以实现实时控制;文献[3]鲁棒性较好且稳态误差小,但有一定的滞后性。对此,文献[4]提出了基于扩张状态观测器(ESO)的LQR控制策略,确保控制对象在复杂环境下的可靠性,但ESO参数的设置具有不确定性,难以获得准确值。文献[5]提出了一种基于线性模型的新型LQR控制器,但计算过程也较复杂,难以有效进行实时控制;另外,反步式控制方法是将整个控制系统分解为若干步,每步都引入一个虚拟控制量,构成函数,使系统稳定,来达到逐渐实现调节和跟踪控制[6−7],文献[8]提出了一种自适应积分反步式控制方法应用于飞行器跟踪期望轨迹,但需要提前估计飞行轨迹路径。实现较高的稳态精度、鲁棒性,精确实时控制的有效途径之一就是采用双回路的控制方法,而控制PID神经元网络是由舒怀林提出的一种新的神经元网络,它同时结合了PID和神经网络的优点[9],在复杂系统的四旋翼飞行器中较为有效。
综上所述,采用PID控制和神经元网络相结合的控制方法对四旋翼飞行仿真器进行研究,设计了一种双回路的四旋翼飞行姿态控制系统,能模拟其在空中的飞行姿态,适合实时飞行仿真和控制算法验证[10]。
2 建立四旋翼仿真器数学模型
四旋翼仿真器(直流电机、电机驱动器、位置编码器、集电滑环、运动控制器、底座和PC机等)中四个电机分布在不同的区域,分别是前后左右,驱动不同的电机会产生不同的运动姿态,有差异的运动姿态所导致的角度变化由实验本体上的位置编码器反馈到运动控制器,运动控制器再将角度变化传递到PC机上控制平台,由PC机上的控制算法对各个电机的速度进行控制,以此形成闭环系统,实现对飞行姿态的精确控制。其三维坐标及实物图,如图1所示。
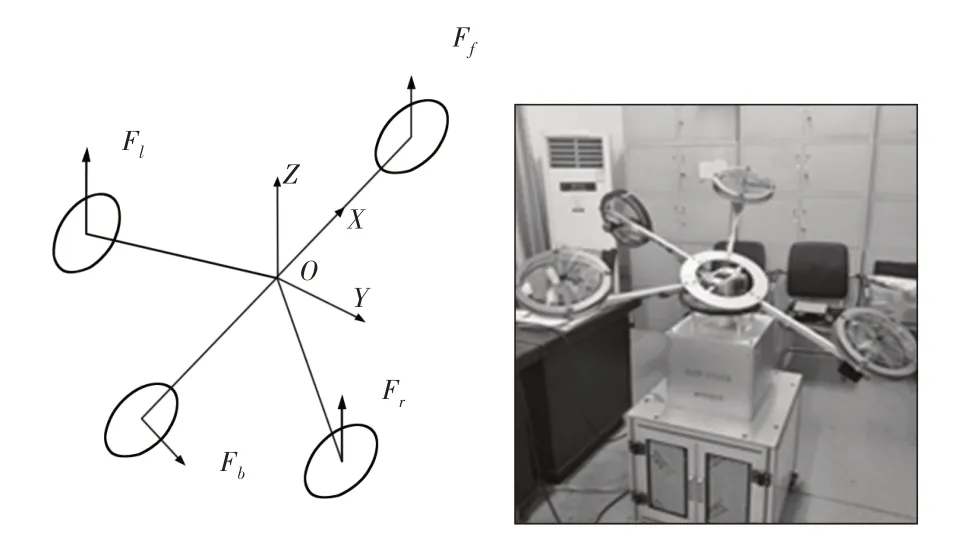
图1 四旋翼飞行仿真器三维坐标图和实物图Fig.1 Three−Dimensional Coordinate and Physical Drawings of Fourrotor Flight Simulator
为了方便数学模型的建立,对其做如下假设:
(1)假设该仿真器为刚体;
(2)假设三个姿态角初始状态为0;
(3)假设该仿真器左右结构对称,且其几何中心和中心重合;
(4)假设旋翼旋转所产生的升力为线性,并忽略摩擦力和旋翼阻尼力矩。
首先,建立四旋翼飞行仿真器三维坐标系,根据三个姿态角的力矩平衡,分别对俯仰轴、滚动轴、偏航轴进行受力分析,其中俯仰轴和滚动轴的受力分析图,如图2、图3所示。

图2 俯仰轴受力分析图Fig.2 Stress Analysis Diagram of Pitch Axis
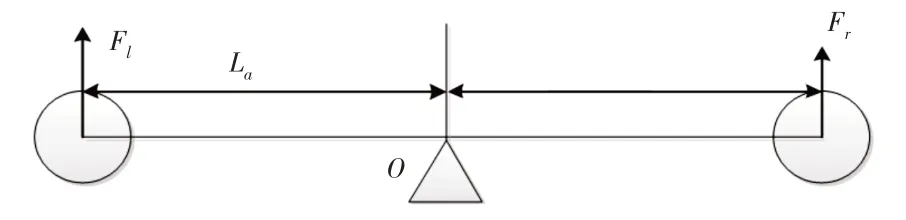
图3 滚动轴受力分析图Fig.3 Stress Analysis Diagram of Rolling Axis
由图2建立俯仰轴力矩平衡方程为:

由图3建立滚动轴力矩平衡方程为:

由于进行偏航运动时,只有后向电机控制其绕Z轴转动来影响偏航角,建立偏航轴力矩平衡方程:


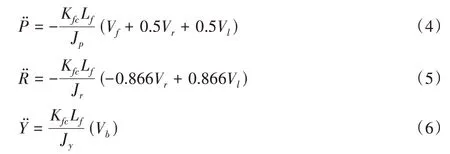
式中:Vf、Vr、Vl、Vb—前向、右侧、左侧、后向电机的电压;Kfc=15,F=KfcV。
最后,通过系统六个状态(俯仰角、俯仰角速度、滚动角、滚动角速度、偏航角、偏航角速度)建立状态方程,系统输入量为:前、后、左、右四个电机的电压,则状态方程为:

其中,四旋翼飞行仿真器参数,如表1所示。

表1 四旋翼飞行仿真器参数表Tab.1 Quadrotor Flight Simulator Parameters Table
3 PID神经元网络控制器的设计
根据建立的四旋翼飞行仿真器的数学模型以及俯仰角、滚动角、偏航角与各个电机之间的关系可知,此系统是一个四输入(前后左右四个电机的电压)三输出(俯仰、滚动和偏航三个轴的角度值)的多变量控制系统,对于这种被控对象,在本文中,使用由三个并联的单个PID神经元组成的四输出PID神经网络控制系统的控制器,而PID神经元网络的四个输出值对应为四旋翼飞行仿真器的控制输入值。
PID神经元网络分为6×9×4结构,结构框图,如图4所示。总共分为三层,第一层(6个神经元),第二层(9个神经元),第三层(4个神经元),各层输入输出情况如下:

图4 四输出PID神经元网络控制系统结构框图Fig.4 Four Output PID Neural Network Control System Structure Diagram

式中:r(k)—系统的给定值;y(k)—实际输出值;Xsi(k)—第一层神经元输出值。
第二层输入为:


PID神经元网络控制器,如图5所示。可以通过MATLAB中S−function 的模块来进行搭建,而S−function 用MATLAB 的M文件来编写[11−12],将编写好的M文件进行模块化,搭建成三输入四输出的控制器。

图5 PID神经元网络控制器Fig.5 PID Neural Network Controller
4 仿真及实时控制实验结果分析
这里通过MATLAB/Simulink实验平台搭建了PID控制器和PID神经元网络控制器模型。
四旋翼飞行仿真器PID神经元网络控制器仿真模型和实时控制模型,如图6、图7所示。
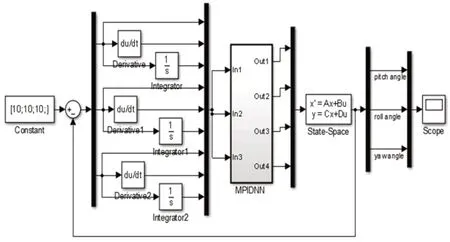
图6 四旋翼PID神经元网络控制器仿真模型Fig.6 Four Rotor PID Neural Network Controller Simulation Model
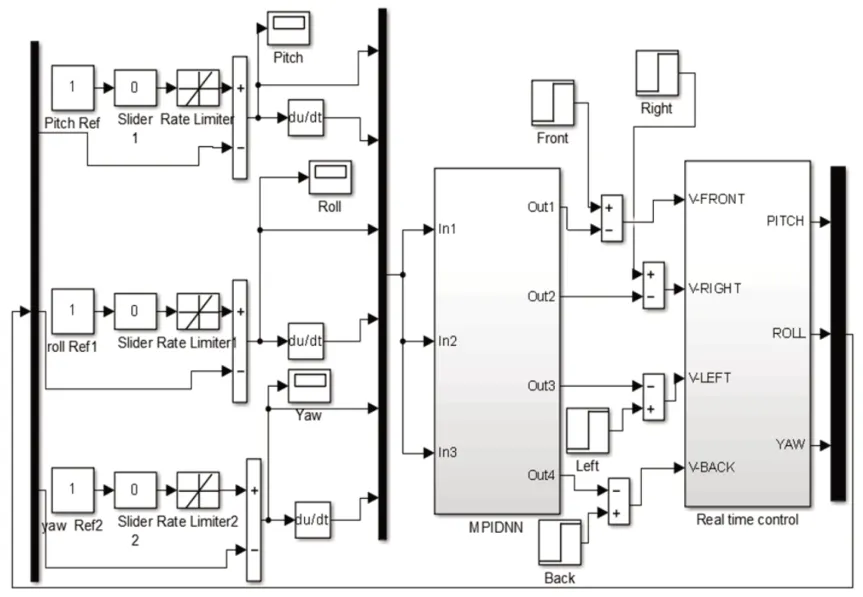
图7 四旋翼PID神经元网络控制器实时控制模型Fig.7 Four Rotor PID Neural Network Controller Real−Time Control Model
在PC机与四旋翼飞行仿真器连接起来的基础上,对其进行仿真和实时控制实验,验证结果可得四旋翼飞行仿真器的仿真曲线图和实时控制系统阶跃响应结果曲线图,如图8、图9所示。

图8 仿真实验结果Fig.8 Simulation Results
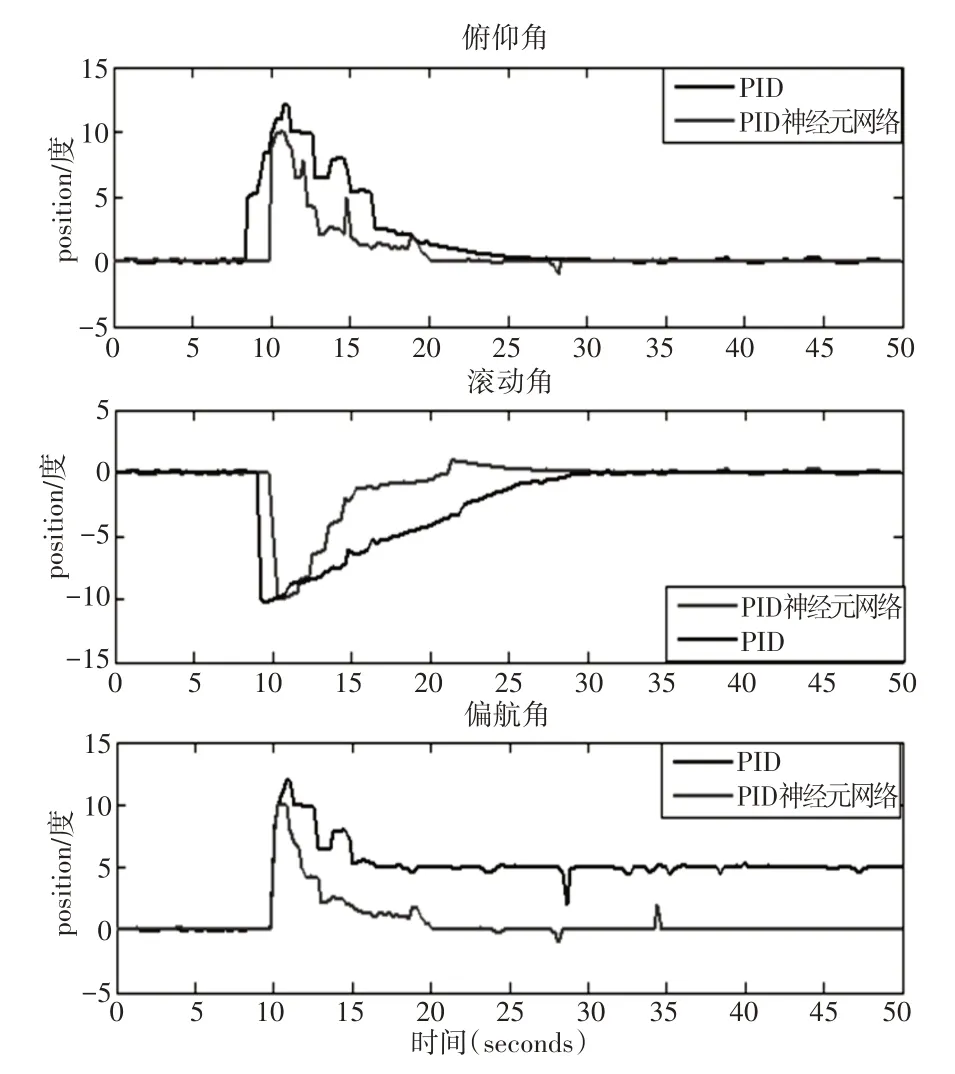
图9 实时控制系统阶跃响应结果Fig.9 Step Response Results of Real−Time Control System
在仿真及实时控制实验中,设俯仰角、滚动角和偏航角给定输入角度为10°,通过PID神经元网络控制系统的控制,俯仰轴调整时间为2.0s,超调量为18%,滚动轴的调整时间为1.5s,无超调,偏航轴调整时间为1.5s,超调量为15%。在实时控制实验中,10s的时候施加阶跃信号,PID 神经元网络控制时,俯仰轴偏转了9.8°,滚动轴偏转了−10.5°,偏航轴偏转了10.1°,系统在20s的时候逐渐恢复到平衡状态;而PID控制时,调节时间要更长,且偏航轴的角会发生一定偏移,稳定在4.8°左右,无法逐步恢复到0°,超调量较大。因此,由实验验证结果可得,PID神经元网络控制相比PID 控制方法,系统的调节时间更短,超调量更小,控制性能更佳。
5 结论
(1)针对四旋翼仿真器的多输入多输出、多变量的复杂系统,将PID和神经网络相结合,设计了基于四旋翼飞行仿真器的PID神经元网络控制器,具有较高的稳态精度、鲁棒性,验证了其系统的可行性和有效性。
(2)在仿真和实时控制实验中,PID控制方法中的三轴偏离量约为4.8°,无法恢复0°,且偏移时间较长,而PID神经元网络控制方法中的三轴偏移量均未超过1°,能逐渐恢复至0°,且偏移时间约2s,其超调量更小、调节时间更短,具有更优的控制性能。
