轧机轧制力的改进训练策略深度神经网络预测
2023-02-09于飞,于博
于 飞,于 博
(1.辽源职业技术学院机电工程学院,吉林辽源 136200;2.长春工程学院机电工程学院,吉林长春 130012)
1 引言
串联式双机架炉卷轧机对钢坯轧制时具有速度快、效率高、温控效果好、占地面积小等诸多优势,轧制力的预测精度对产品厚度、板型质量具有决定性影响,但是轧制力的影响因素较多且相互高度耦合,使轧制力预测精度较低[1]。研究轧制力的高精度预测方法对于提高轧制产品质量具有重要意义。
轧制力预测方法可以分为两大类:(1)建立预测的解析模型;(2)机器学习法进行拟合,其中机器学习法根据网络深度分为浅层拟合和深度拟合。文献[2]使用滑移线场划分轧制件塑性区,使用Hencky应力方程推导出了轧制力解析解,得到了较高精度的功率预测值和形状参数预测值。文献[3]将有限元与神经网络结合应用于轧制力预测,轧制力预测误差控制在了10%以内。文献[4]提出基于极限学习机−自动编码器的轧制力预测方法,使用自编码器提取原始数据特征,使用极限学习机进行轧制力回归,提高了轧制力预测精度。
文献[5]针对热连轧的轧制力预测问题,构建了深度前馈神经网络预测模型,实现了轧制力的高精度预测。以上轧制力预测方法都具有较高精度,其中由于浅层网络的表达和拟合能力有限,因此预测精度一般小于深度网络,但是深度网络存在非凸优化和梯度弥漫问题,仍是需解决的重要问题。
针对双机架炉卷轧机的轧制力预测问题,提出了改进深度神经网络的预测方法。在多层BP神经网络基础上,提出了随机小批量梯度下降法和自适应矩估计梯度优化算法,达到了提高训练速度和预测精度的目的。
2 轧制力影响参数分析
2.1 轧制工艺流程
这里研究对象为TIPPINGS公司设计的1725mm双机架炉卷轧机,此轧机可轧制碳素钢、合金钢等各种钢材,本文使用材料为Q235。轧机的生产参数,如表1所示。

表1 制件工序Tab.1 Process of Workpiece
双机架炉卷轧机的轧制工艺流程,如图1所示。首先将连铸板坯送入到加热炉中,加热到设定温度后取出,而后在除磷箱中使用高压水去除加热产生的氧化铁皮,之后送入到轧机进行轧制。板坯在入口处对中后才能够进入轧制,Q235钢经过7个道次的轧制才能够使其厚度达到要求范围内。轧制完毕后进行冷却、卷取、运输等。另外,图中的立辊轧机作用是控制轧件宽度和平稳度。
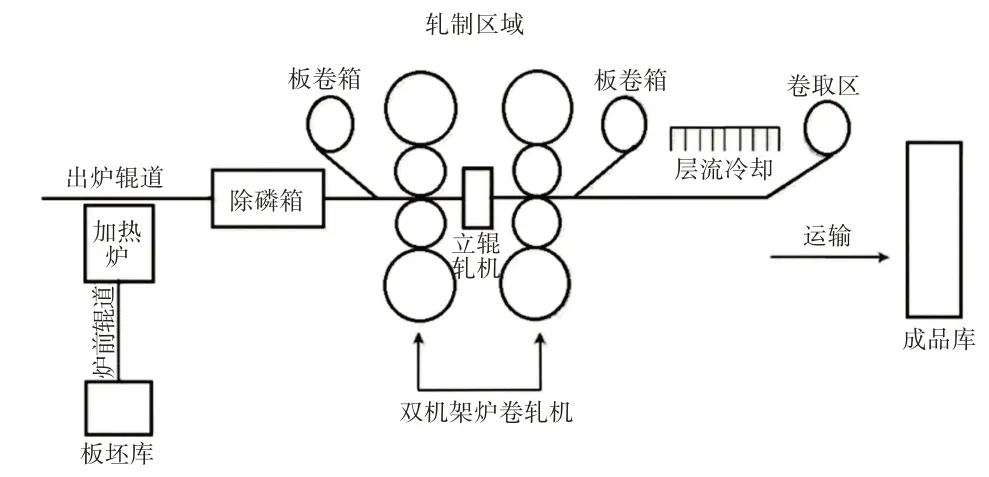
图1 轧制工艺流程Fig.1 Rolling Technology Process
2.2 轧制力影响参数分析
参考文献[6−7]可知,最具代表性的轧制力计算模型为SMIS公式,即:

式中:P—轧制力;B—板坯初始宽度;—轧辊与钢坯接触面在水平方向的投影长度;Qp—应力状态影响系数;K—变形阻力;KT—轧制力影响系数。
上述参数中,B和决定了受力面积的大小,由轧辊半径R、板坯入口厚度h0和出口厚度h等因素决定。Qp和KT是决定轧制力大小的力学因素,其中KT受前后张力影响。变形阻力K表示轧件的受热温度T、自身化学成份等对轧制力的影响系数,影响因素包括板坯化学成份、轧制温度T、轧制速度Vr等。经以上分析,轧制力影响因素包括板坯初始宽度B、轧制温度T、轧制速度Vr、板坯入口厚度h0、出口厚度h、轧辊半径R、应力状态影响系数Qp等7个参数及板坯化学成份等。经主元素分析法分析,最终确定以上7个参数和化学成份中C、Mn、Si元素含量等共10个参数作为网络输入,用于预测轧制力。
3 改进深度神经网络
本节针对深度神经网络训练时出现的振荡和陷入局部最优等问题,提出了随机小批量样本选取和自适应矩估计梯度下降法,使深度神经网络能够稳定地训练出最优参数。
3.1 深度神经网络
这里使用多层BP神经网络构造深度神经网络,由输入层、多隐藏层、输出层组成[8],如图2所示。神经网络对复杂函数的拟合能力随隐藏层数的增加而增强,但是计算复杂度和训练困难也会增加[9]。
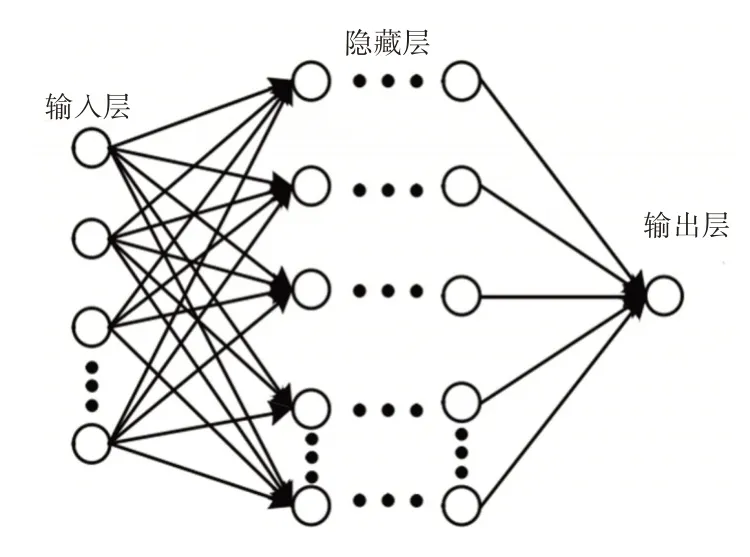
图2 深度神经网络结构Fig.2 Deep Neutral Network Structure
对于K+1层神经网络,k=0表示输入层,k=[1,k−1]表示隐藏层,k=K表示输出层,每层神经元数量记为nk。第k−1层向第k层的传递权值记为Wk,第k层神经元阈值记为Bk,第k层神经元输入值记为Zk,激活值记为Ak,则网络的前向传递为:
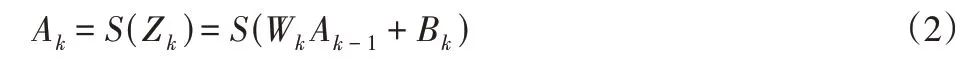
式中:S()—激活函数,一般使用Sigmoid函数或Tanh函数。
基于BP算法的误差反向传播参数训练为[10]:
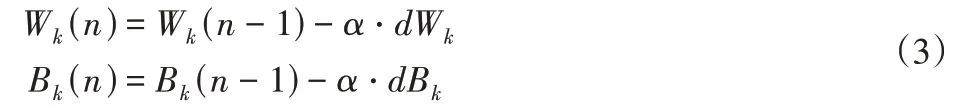
式中:n—训练迭代次数;α—学习率;dWk、dBk—各自的参数梯度。
3.2 随机小批量梯度下降法
对于参数训练,根据样本使用方法的不同,分为批量梯度下降法和随机梯度下降法。
批量梯度下降法[11]由于全训练数据的使用能够更加准确地搜索参数最优值,减小梯度训练过程中的振荡。但是面对大数据集时,由于全训练数据的参与,参数每次训练时将全体数据载入,产生了巨大的计算负担,降低了网络的训练效率和收敛速度。同时,容易产生过拟合问题。
随机梯度下降法在每次训练时,随机选取一个样本进行训练[12]。这种训练方法速度较快,计算压力极小。但是可能出现使用较少样本时已获得较好损失函数的问题,也即训练样本无法充分使用。
另外,样本选取的随机性为网络引入了噪声,训练时容易产生振荡现象,如图3所示。

图3 随机梯度下降法迭代过程Fig.3 Iteration Process of Stochastic Gradient Descent
为了实现批量梯度下降法与随机梯度下降法的优势互补与劣势互消,这里提出了随机小批量梯度下降法,其主要思路为:将所有的训练样本随机分为H个子集{}Xh,Yh,h=1,2,…,H,每次抽取一个子集用于参数训练,当所有子集均参与训练时,训练过程结束,评价函数为所有子集损失函数的平均值。随机小批量梯度下降的迭代效果,如图4所示。对比图4与图3可以看出,随机小批量梯度下降法在迭代过程中的振荡明显小于随机梯度下降法,同时子集的选取具有一定随机性,这种随机性减小了陷入局部最优的概率;另外,随机小批量梯度下降法也具有训练集的完整性。
图4 随机小批量梯度下降法迭代过程Fig.4 Iteration Process of Stochastic Mini−Batch Gradient Descent
3.3 自适应矩估计梯度优化算法
上节给出了训练样本的划分方法,本节给出在子训练集内的具体训练方法。神经网络随着深度的增加,其局部极值点和鞍点也成倍增加。传统的梯度下降法(即BP算法)在应对多局部极值的优化问题时,极易陷入局部最优点或鞍点,为了解决这一问题,本文提出了自适应矩估计梯度优化算法。其核心思想为:使用指数移动平均法估计误差梯度的均值(一阶矩)和方差(二阶矩),使用梯度均值与方差的无偏估计构造参数训练值。
自适应矩估计梯度优化算法的实现步骤为:
(1)初始化参数,包括参数向量θ(0)=[W,B],梯度一阶矩初值Mdθ(0),梯度二阶矩初值Udθ(0),训练迭代次数t=0;
(2)令t=t+1,计算损失函数对参数的梯度g(t),即:

式中:∇θ−对θ求梯度;f()−损失函数。
(3)使用指数移动平均法估计误差梯度的均值和方差为:

式中:Mdθ(t)—梯度均值估计值;Udθ(t)—梯度方差估计值;β1—一阶矩的指数衰减速度;β2—二阶矩的指数衰减速度,g2(t)=g(t)⊗g(t)—g(t)与g(t)的卷积。
(4)对误差梯度的均值和方差进行偏差修正,得到两者的无偏估计,为:

式中:α—学习率;ε—极小数,防止除数为0。重复(2)~(5),直至达到最大迭代次数。
3.4 改进深度神经网络结构
网络的输入参数共10个,输出参数为轧制力预测值,因此输入层神经元数量为10,输出层神经元数量为1。为了得到较好的参数拟合能力,网络设置为5层隐藏层。从输入到输出的神经网络结构为[10,128,128,64,64,32,1]。后文预测效果验证时,为了保证公平,传统深度网络与改进训练策略深度网络使用同一结构,但是训练方法不同。
隐藏层激活函数使用Relu 函数,输出层激活函数使用tanh函数。随机小批量梯度下降法中,训练子集规模设置为60。误差反向训练时,学习率α=0.001,一阶矩的指数衰减速度β1=0.9,二阶矩的指数衰减速度β2=0.999,极小数ε=10−7。
参数训练的损失函数为:

式中:f—损失函数;m—样本数量;yi—期望输出值;yi′—网络实际输出值。
4 实验验证及分析
4.1 案例设计
根据2.1节介绍,Q235钢经过7个道次的轧制可以达到设定厚度,这里以第1道次的1号轧机为研究对象,对深度神经网络的轧制力预测效果进行验证。轧制的初始参数设置,如表2所示。

表2 轧制参数设置Tab.2 Parameters Setting of Rolling Process
在现场的轧制过程中,采集1200组实验数据进行预测效果验证。其中的9000组数据作为训练样本,3000组数据作为测试样本。
4.2 结果对比与分析
使用相同结构的深度神经网络和改进深度神经网络对轧制力进行预测,传统深度神经网络使用批量梯度下降法和BP算法的参数训练方法,改进神经网络使用随机小批量梯度下降法和自适应矩估计梯度优化的参数训练法。两者的训练过程,如图5所示。

图5 训练过程Fig.5 Training Process
由图5可以看出,传统深度神经网络算法的训练速度差于改进神经网络,这是因为传统算法使用的批量梯度下降法每次迭代均使用所有的训练样本,造成了极大的计算负担,使算法的训练效率低;而改进深度神经网络使用随机小批量梯度下降法,每次迭代使用一个子集,参数的训练效率较高。
另外,传统深度神经网络算法的训练最终陷入局部最优,参数的训练能力明显差于改进深度神经网络,这是因为BP训练算法容易陷入局部最优点或鞍点,而改进深度神经网络使用的自适应矩估计梯度优化法有效解决了这一问题,使得改进深度神经网络的参数优于传统深度神经网络。
传统神经网络与改进神经网络的预测结果对比,如图6所示。

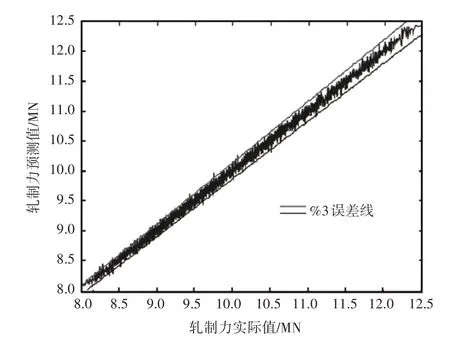
图6 预测结果对比Fig.6 Comparison of Predicting Result
统计两者算法的最大预测误差、平均预测误差、训练耗时,结果,如表3所示。

表3 预测结果Tab.3 Predicting Result
结合表3和图6可知,传统深度神经网络的预测误差绝大部分分布在5%以内,最大相对误差为5.8%,平均误差为2.2%,训练时间为862.93s;而改进深度神经网络的预测误差绝大部分分布在3%以内,最大误差为3.4%,平均误差为1.0%,训练时间为226.15s。
以上数据表明了改进深度神经网络的预测精度和训练速度均优于传统深度神经网络,也证明了改进深度神经网络在轧制力预测中的有效性。
5 结论
这里研究了双机架炉卷轧机的轧制力预测问题,提出了改进深度神经网络的预测方法。经验证得出以下结论:
(1)随机小批量梯度下降法的训练效率高于批量梯度下降法;
(2)自适应矩估计梯度优化算法的参数训练效果优于传统梯度下降法;
(3)改进深度神经网络的训练速度和预测精度优于传统深度神经网络。
