变压器的故障预测研究
2023-02-09陈长征
王 磊,陈长征
(沈阳工业大学机械工程学院,辽宁沈阳 110870)
1 引言
电力变压器是电力系统的重要组成部分,如果出现故障,将给社会带来巨大的经济损失。因此,降低变压器的故障率,保证变压器安全可靠的运行。利用相关算法判断变压器什么时间发生故障以及发生何种类型的故障具有重大的实际意义。
目前,国内外的变压器故障预测方法较少,主要通过灰色理论对变压器故障进行预测。文献[1]利用油中溶解故障气体分析法检测的H2,CH4,C2H6,C2H4,CO2,C2H2,CO等7种故障气体的历史数据建立灰色多变量预测模型,利用预测模型对变压器油中溶解的故障气体浓度进行了预测;文献[2]将H2,CH4,C2H6,C2H4,C2H2等5种故障气体作为主要特征气体,基于灰色理论和BP神经网络建立变压器故障预测模型,预测了5种故障气体的变化趋势值;基于灰色理论的变压器故障预测具有不需要大量样本、样本不需要有规律的分布、计算工作量小、等优点,但基于灰色理论的变压器故障预测只适合短期预测,当基于灰色理论对变压器故障进行中长期预测时,预测的准确率较低。
随着大数据时代的到来,深度神经网络被证明对原始数据具有强大的提取能力。其中,LSTM神经网络是一种用于处理时间序列的深度神经网络,能够全面的利用时间序列的相关性,准确的预测变量在未来时间段的输出值[5]。目前,该神经网络算法已经广泛应用到声音识别、语言预测等领域。
2 油中溶解气体的关联性分析
电力变压器的主要故障为热故障和电故障,当变压器运行时,如果发生电故障或热故障,则变压器油中会产生与故障相关的7种故障气体,分别为CH4,C2H6,C2H4,CO2,C2H2,CO,H2。通过对7种故障气体的分析,可以判断出变压器所处何种故障类型。因此,变压器不同故障气体之间是相互关联、相互影响的。
本节基于表1变压器油色谱在线监测系统监测70天的不同故障气体浓度来分析不同故障气体之间的联程度。
变压器油中不同故障气体之间的关联度用相关系数r表示,相关系数r的原理为式(1)。
当两个时间序列相关系数小于0.5时,则认为两个时间序列无关联,当两个时间序列相关系数大于0.5时,则认为两个时间序列相关。基于表1所示的变压器油色谱在线监测数据,利用关联度公式,计算不同故障气体之间的关联度,结果,如图1所示。
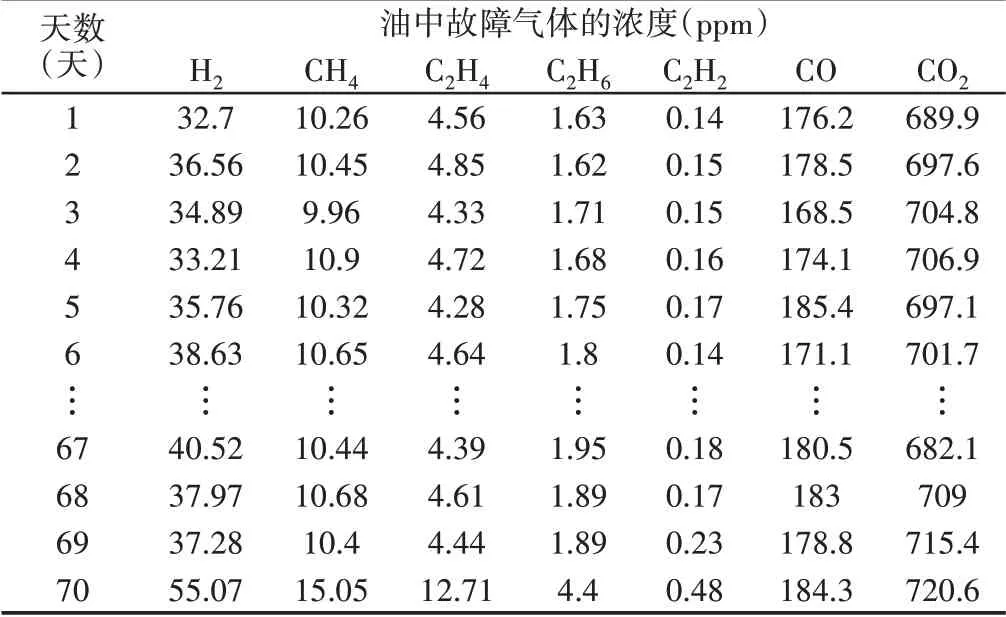
表1 某220kV变压器故障气体浓度监测数据Tab.1 Monitoring Data on Gas Concentration of a 220kV Transformer Fault
图1中x和y坐标的1,2,3,4,5,6,7分别代表H2,CH4,C2H4,C2H6,C2H2,CO,CO2的时间序列。根据图1可知,当时间序列x和时间序列y相同时,相关系数r均大于0.5,两个序列不同时,相关系数均大于0.5。因此,可以得出结论:当前时间七种故障气体浓度对未来时间每种故障气体浓度影响非常大,因此,可以根据当前时间七种故障气体浓度来预测每种故障气体未来时间的浓度。

3 深度LSTM神经网络模型
深度LSTM神经网络是由输入层、多个隐藏层、输出层组成,每个隐藏层由多个LSTM 单元组成。能自动提取时间序列数据特征,已经广泛应用到声音识别、语言预测等领域,网络结构,如图2所示。

图2 深度LSTM神经网络结构Fig.2 Depth LSTM Neural Network Structure
3.1 LSTM神经网络
LSTM单元是由遗忘门、输入门和输出门组成。输入门的作用是保留多少当前时刻的输入信息到当前时刻的单元状态;遗忘门的作用是保留多少上一时刻的单元信息到当前时刻的单元状态;输出门的作用是决定当前时刻的单元状态有多少输出。LSTM网络单元的结构图,如图3所示。包含了三个输入和两个输出,三个输入分别为:上时刻单元细胞状态ct−1、上时刻单元输出值ht−1、当前时刻单元输入值xt。两个输出分别为当前时刻单元细胞状态ct、当前时刻输出值ht。σ和tanh是两种激活函数,σ为sigmoid 函数,tanh为双曲正切函数。计算方式为式(2)和式(3),σ激活函数目的是把输入信息映射到(0~1)之间,tanh激活函数的目的是把输入信息映射到(−1~+1)之间。

图3 LSTM单元网络结构Fig.3 Network Structure of LSTM Unit
遗忘门计算原理为式(4);输入门计算原理为式(5)、式(6)、式(7);根据输入门和遗忘门的输出以及前一时刻单元的细胞状态可得到当前时刻的细胞状态,计算方式为式(8),基于当前时刻细胞状态和当前时刻单元的输入以及前一时刻单元的输出可得到当前时刻单元的输出(输出门的输出),其计算原理,式(9)、式(10)所示。
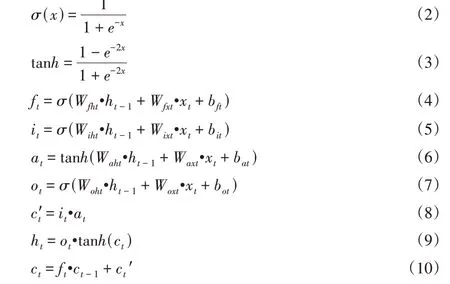
式中:ft—t时刻遗忘门的输出向量值;bft—遗忘门的偏置向量;Wfht—上一个单元输出对应t时刻遗忘门的权值矩阵;it—t时刻输入对应遗忘门的权值矩阵;Wfxt—t时刻输入向量与前一时刻输出向量经sigmoid 层的输出值;bit—t时刻sig‐moid 层的偏置向量;Wiht—上一个单元输出对应t时刻sig‐moid层的权值矩阵;Wixt—t时刻输入对应sigmoid层的权值矩阵;at—t时刻输入向量与前一时刻输出向量经tanh层的输出值;bat—t时刻tanh层的偏置向量;Waht—上一个单元输出对应t时刻tanh层的权值矩阵;Waxt—t时刻输入对应tanh层的权值矩阵;c′t—t时刻输出门的输出值;ct—t时刻单元的细胞状态;ct−1—t−1时刻单元的细胞状态;ot—t时刻输入向量与前一时刻输出向量经σ层的输出值;bat—t时刻σ层的偏置向量;Woht—上一个单元输出对应t时刻σ层的权值矩阵;Waxt—t时刻输入对应σ层的权值矩阵;ht—t时刻单元的输出向量。
3.2 梯度下降法的改良
若学习率的选择过大,利用梯度下降法优化神经网络的权值和偏置会导致权值和偏置在目标函数的极值点两侧不断震荡,不易寻求最优的权值和偏置;若学习率的选择过小,则网络训练时间较长。
因此需要对学习率进行自适应调整,这里在随机梯度下降算法的基础上,采用变化的学习率并加入动量项来优化神经网络的权值和偏置值。
每次迭代采用变化的学习率原理是指先设置一个初始学习率,若迭代一次后,误差函数增加,则将学习率乘以一个小于1的常数β;若迭代一次后,误差函数减小,则将学习率乘以一个大于1的常数ϕ,计算原理为式(11)。
在变化学习率的基础上,在梯度下降迭代式的后面添加动量项来解决梯度下降法的不足。其原理为式(12)。

式中:ηl—网络第l次迭代的学习率;ηl−1—第l−1次网络迭代的学习率;ϕ—学习率的调整因子;β—学习率的调整因子;Wl—网络第l次迭代的权值矩阵;Wl−1—网络第l−1次迭代的权值矩阵;α—动量初始值;dl—第l次迭代总误差负梯度方向,即:dl=−∇E总(w);
3.3 基于深度LSTM神经网络的预测模型
根据第一节变压器油中溶解故障气体的相关性分析结果,可根据深度LSTM 神经网络建立油中溶解故障气体浓度的预测模型。预测每种故障气体时,模型的输入层为当前时刻7种故障气体的浓度值,输出层为下一时刻要预测气体的浓度值。预测模型的训练步骤如下:
(1)将收集的H2,CH4,C2H6,C2H4,CO2,C2H2,CO 浓度值数据划分为训练样本和测试样本;
(2)将各故障气体浓度数据进行归一化;
(3)初始化网络的权值和偏置值,前向计算网络的预测值。
(4)依据沿时间的反向传播算法计算网络中权值和偏置的梯度,利用3.2节改良的梯度下降算法获得新的权值和偏置。
(5)得到最优的预测模型。
4 算例分析
4.1 数据分析
这里将搜集的220kV变压器油中溶解故障气体浓度数据进行整理,共整理300 组数据,每一组数据包含CH4,C2H6,C2H4,C2H2,H2,CO,CO2等7种故障气体连续70天的浓度值。从300组数据中随机选取240组数据样本作为变压器故障气体浓度预测模型的训练样本,随机选取60组数据样本作为变压器故障气体浓度预测模型的测试样本。利用7 个LSTM 神经网络模型对CH4,C2H6,C2H4,C2H2,H2,CO,CO2等7种故障气体浓度进行预测。限于文章篇幅,以预测H2的模型为例展开分析。
4.2 预测模型评价指标
这里采用均方根误差函数作为变压器油中溶解故障气体浓度预测模型的评价指标,根据LSTM神经网络模型的预测值与真实值的均方根误差来判断网络模型的优劣。均方根误差函数,如式(13)所示。

式中:e—数据样本平均误差;n—预测数据样本个数;yi—每种油中溶解气体浓度的真实值—每种油中溶解气体浓度的预测值;
4.3 预测模型时间步个数的确定
根据4.1节搜集的变压器油中溶解气体浓度数据,对变压器油中溶解的H2进行预测,预测H2的深度LSTM神经网络模型的参数值,如表2所示。当网络设置为不同时间步时,测试数据样本的均方根误差不同,不同时间步的深度LSTM神经网络预测模型对应的测试样本均方根误差,如图4所示。

表2 预测H2的深度LSTM神经网络模型的参数值Tab.2 Parameter Values of Depth LSTM Neural Network Models Predicted H2
根据图4可知,深度LSTM神经网络预测模型在网络结构确定的情况下,随着时间步的增加,测试样本的均方根误差逐渐下降,当时间步增加到15天时,测试样本的均方根误差达到最低,伴随着时间步的继续增加,均方根误差没有太大的波动,当时间步增加到31天时,均方根误差出现上升趋势。因此,可确定网络模型最佳的时间步为31天。

图4 不同时间步的预测模型对应的均方根误差Fig.4 Root Mean Square Error Corresponding to Prediction Models for Different Time Steps
4.4 预测模型网络结构的确定
LSTM 神经网络模型隐藏层个数决定着预测模型性能的好坏,在合理范围内,隐藏层个数越多,数据提取能力越强,LSTM神经网络模型预测性能越好。但是,当隐藏层个数过多,LSTM神经网络预测模型容易出现过拟合现象。因此,为了确定合理的H2预测模型隐藏层个数,本节采用31个时间步,(1~6)个隐藏层建立不同的LSTM神经网络预测模型,研究不同网络深度对网络模型的影响,不同隐藏层的深度LSTM神经网络的测试样本误差结果,如图5所示。
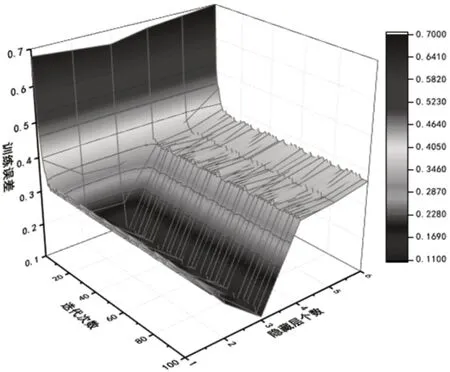
图5 不同隐藏层神经网络的测试样本误差Fig.5 Relationship Between the Number of Different Hidden Layers and the Training Error
根据图5可知,当时间步确定的情况下,隐藏层个数由一层增加到三层时,随着迭代次数的增加,训练误差逐渐下降;隐藏层个数从四层到六层时,随着迭代次数的增加,训练误差相对于三层隐藏层呈上升趋势;由此可得出结论:预测H2的深度LSTM神经网络预测模型的最优隐藏层个数为3层。
综合以上分析,将预测H2的深度LSTM神经网络模型的时间步设置为31,网络层数设置为5层,基于不同的隐藏层神经元个数建立H2预测模型,得到的不同网络结构对应的测试样本均方根误差,如图6所示。
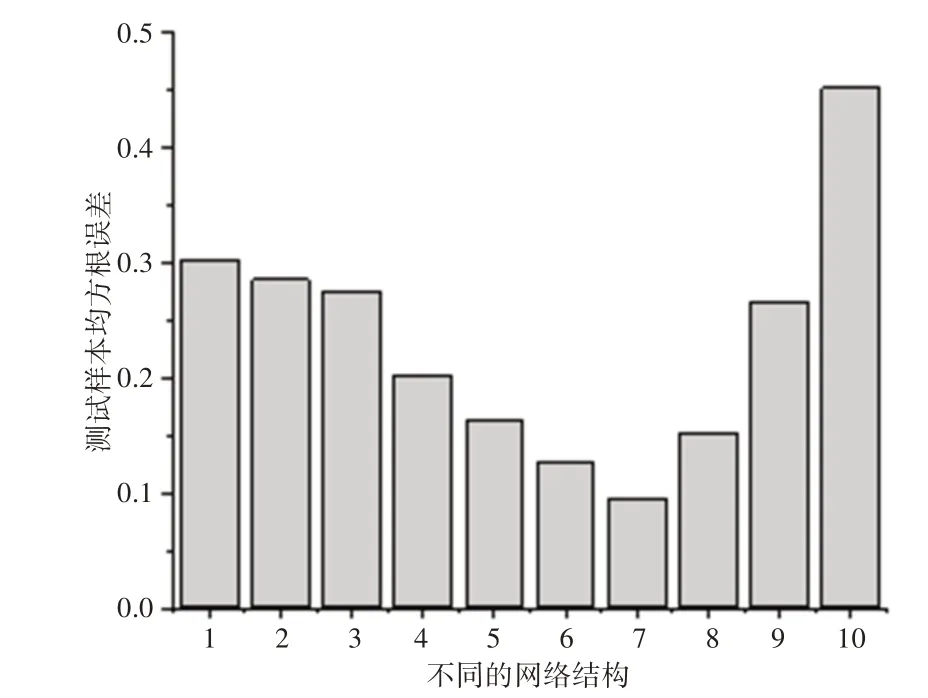
图6 不同网络结构对应的测试样本均方根误差Fig.6 Prediction of Root−Mean−Square Errors in Different Network Structures of H2
图6的横坐标1,2,3,4,5,6,7,8,9,10分别代表的网络结构为7−15−20−25−1、7−20−25−30−1、7−25−30−35−1、7−30−35−40−1、7−35−40−45−1、7−40−45−50−1、7−45−50−55−1、7−50−55−60−1、7−55−60−65−1、7−6−5−4−1。通过对图6 分析,可以得到每个时间步最优的网络结构为7−45−50−55−1。
4.5 与多变量灰色预测模型对比
为验证这里所述的变压器油中溶解气体预测效果,将上述得到的最优深度LSTM 神经网络预测模型与多变量灰色预测模型进行对比。利用深度LSTM 神经网络预测模型与多变量灰色预测模型对2014年7月5日到2014年9月1日的故障气体浓度进行预测,两种预测方法预测的均方根误差结果,如图7所示。
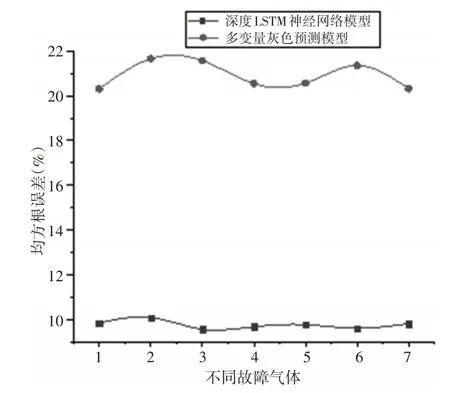
图7 两种预测方法预测的均方根误差Fig.7 Root−Mean−Square Error for Different Fault Gases Predicted by Both Methods
图7横坐标的1,2,3,4,5,6,7分别表示H2,CH4,C2H6,C2H4,C2H2,CO,CO2。由图7 可知,深度LSTM 神经网络预测模型优于多变量灰色预测模型。并且深度LSTM 神经网络预测模型预测的故障气体浓度均方根误差均不超过10%,因此,深度LSTM 神经网络预测模型能够较准确地预测变压器油中溶解的故障气体浓度,继而对变压器故障进行预测。
5 结论
这里研究了不同故障气体之间的相关系数,利用搜集的不同时刻故障气体浓度建立了深度LSTM神经网络预测模型,对模型的结构进行了优化,得到了最优的油中溶解气体预测模型,并利用相同数据对基于深度LSTM 神经网络建立的故障预测模型与基于多变量灰色预测建立的故障预测模型进行对比。根据对比结果可得出结论:深度LSTM神经网络预测模型优于多变量灰色预测模型,能够准确地预测变压器油中溶解故障气体浓度,为变压器故障预测提供依据,是非常有效的变压器故障预测方法。
