磁力T型压电俘能器参数共振及其特性研究

邹 政，马 戈，汪 灿，谢 进

（西南交通大学机械工程学院，四川成都 610031）

1 引言

近年来，振动能量收集的研究引起人们的广泛关注[1−2]。通常将振动能量转化为电能的装置称为俘能器。由于压电俘能器具有结构简单、无污染、寿命长、易于实现装置的微小化等优点而成为了研究热点[3]，其最常见结构为压电悬臂梁。

环境中的振动是多方向，现有的研究大多是研究直接激励（激励方向垂于梁长）下的压电俘能器，而对于参数激励（激励方向平行于梁长）的研究较少。

文献[4]建立了参数激励下的压电俘能器集总参数模型，通过解析法和实验研究了多个参数对俘能器的影响。

文献[5]推导了受参数激励悬臂梁的非线性分布参数模型，考虑了几何、惯性、压电材料等多种非线性因素的影响。与直接激励相比，参数激励引发的参数共振具有能将输出功率提高一个数量级的潜力，但需要克服和阻尼相关的激励阈值，否则系统不能发生参数共振，进而稳态响应趋向于0。

文献[6−7]采用实验的方法，利用弹簧放大振动激励，进而降低了参数共振的激励阈值，但是俘能带宽比较窄。

为了降低参数共振的激励阈值，并拓展能量俘获的频率带宽，提出了一种磁力T型压电俘能器。

采用数值方法，分析、对比磁力T型双梁压电俘能器以及作为其特例的参数激励单梁俘能器的俘能特性，从而说明磁力T型双梁压电俘能器在降低阈值和拓展俘能带宽的主要优点。

2 磁力T型压电俘能器动力学模型建立

2.1 磁力T型压电俘能器的物理结构

所提出的磁力T型压电俘能器，如图1所示。

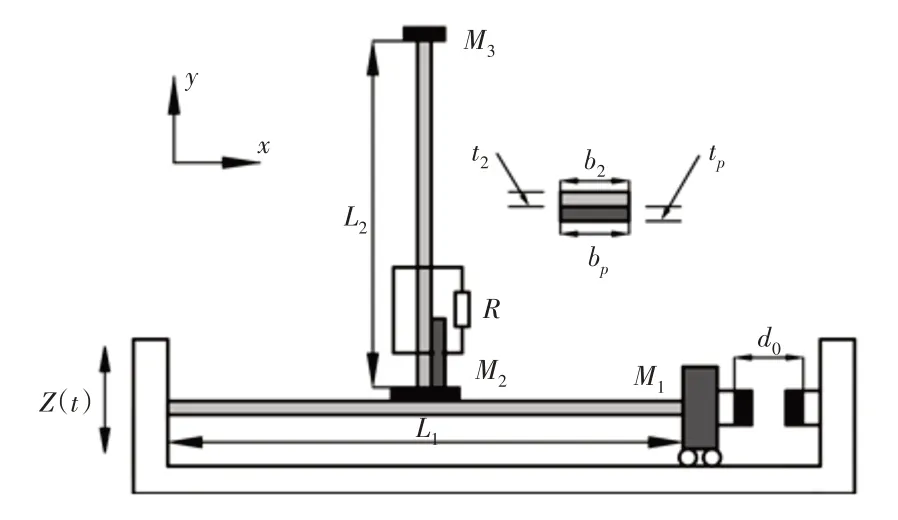
图1 磁力T型压电俘能器结构示意图Fig.1 Structure Diagram of Magnetic T−Shaped Piezoelectric Energy Harvester

该俘能器的水平梁1与竖直梁2正交，在梁1右端部有一个可以移动的质量块，质量块上附着磁铁，磁铁和质量块的总质量为M1，磁铁的初始间距为d0。

梁2的下末端位于为梁1的中部，通过质量块M2与梁1连接，梁2的上末端装有质量块M3。梁1的长度为L1，厚度为t1，宽度为b1。梁2长度为L2，长度为Lp的压电片贴在梁2的下末端，梁2基底层和压电层的宽度分别为b2、bp，厚度分别为t2和tp。

压电层由厚度可忽略的平面电极与负载电阻R相连，连接方式采用并联，其产生的电压为V。

2.2 磁力T型压电俘能器动力学方程

在外部谐波激励z（t）的作用下，梁1和梁2的一阶振型，如图2所示。

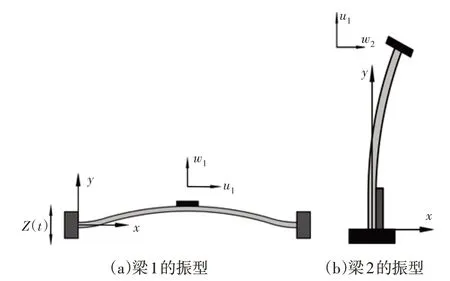
图2 系统振动时梁1和梁2的振型Fig.2 Vibration Modes of Beam 1 and Beam 2 During System Vibration

梁1产生的横向和轴向位移分别为w1（x，t）和u1（x，t）；梁2的横向和轴向位移分别为w2（y，t）和u2（y，t）。

根据图2，考虑梁1和梁2的横向位移w1和w2的一阶展开式，其表达式分别为：

式中：X（t）和Y（t）—梁1和梁2的位移幅值，即广义坐标。系统的机电耦合动力学方程可由扩展哈密顿原理推导。根据扩展哈密顿原理[8]，得：

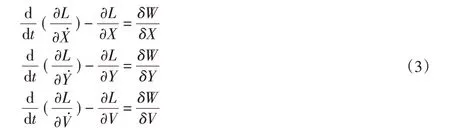
式中：L—拉格朗日函数，其计算式为：L=T－U；

T—系统的动能；U—系统的势能；

δW—非保守力所做的虚功的变分。

为此，首先计算系统的动能和势能，系统的动能为：

式中：TL1、TM1、TM2、TL2、TM3—梁1、质量块M1、质量块M2、梁2 及质量块M3的动能，其计算式分别为：

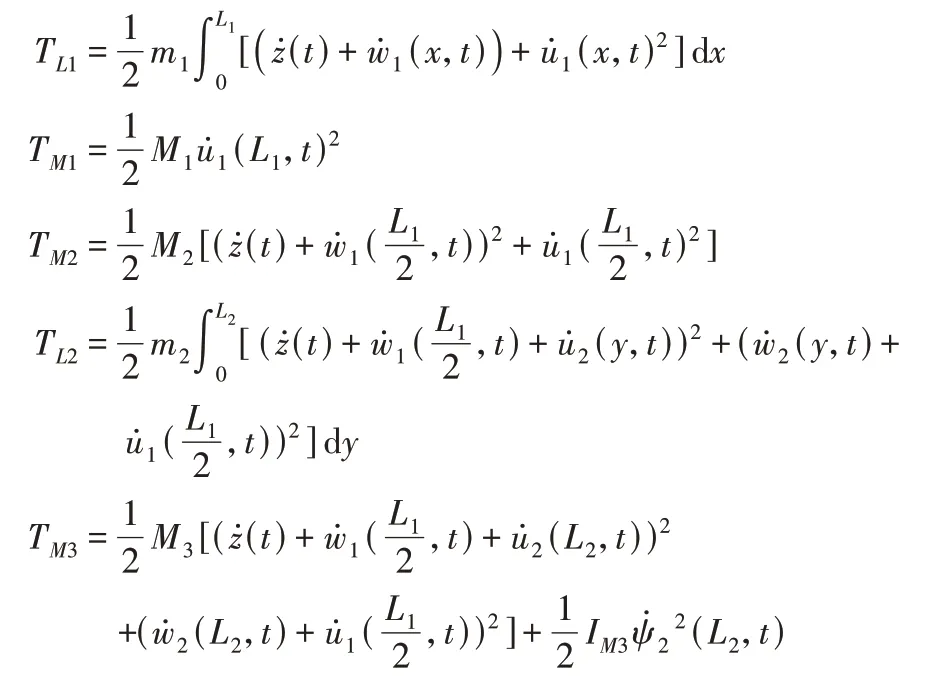
式中：m1和m2—梁1和梁2单位长度的质量；IM3—质量块M3的转动惯量；ψ2—梁2的转角。

在考虑重力势能时，系统的势能为：

式中：U1、U2、UG、Um—梁1、梁2 的势能以及重力势能和磁势能。

在考虑梁的几何非线性[9]时，U1、U2和UG的计算式分别为：

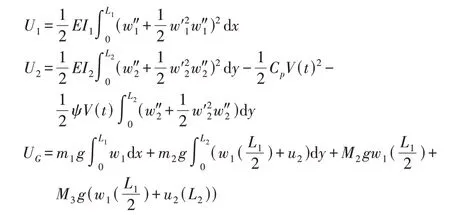
式中：E1I1，E2I2—梁1和梁2的抗弯刚度；E1和E2—梁1和梁2的杨式模量；ψ—机电耦合系数；Cp—压电电容，这些参数的具体表达式见文献[10]；V（t）—系统产生的电压。

非保守力所做的虚功的变分可以表示为：

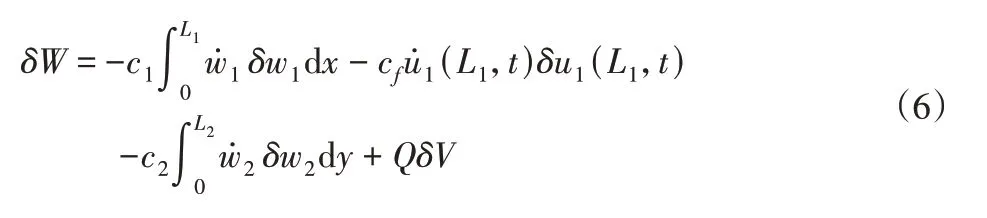
式中：c1和cf—梁1的粘性阻尼以及梁1右端质量块所受的滑动摩擦阻尼；c2—梁2的粘性阻尼；Q—压电层的电荷输出，Q与负载电阻R之间满足=V/R。

磁势能Um可以采用磁偶极子模型推导，其计算式为：

式中：µ0—真空磁导率；rBA—磁铁A中心到磁铁B中心的向量；mB和mA—磁铁B和A的磁矩向量。具体表达式为：

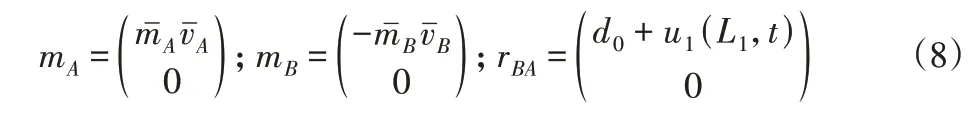
根据文献[5]可知，梁1和梁2的横向位移和纵向位移应满足：

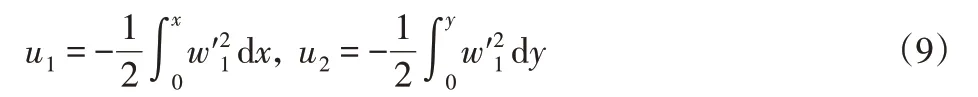
将式（1）、式（8）和式（9）代入式（7），利用泰勒公式在X=0处展开并保留到4次项，有：

将式（1）～式（2）、式（4）～式（6）和式（9）代入式（3）可以得到磁力T型压电俘能器的动力学方程为：

式中：k1、g1—梁1和梁2的等效质量；C1、C2—梁1和梁2的等效阻尼；Cf—等效滑动摩擦阻尼；k2−K1、k3—梁1的等效刚度；g2、g3—梁2的等效刚度；k4、g4—梁1和梁2的惯性非线性系数；k5、k6、g5、g6—梁1和梁2的非线性耦合项系数；k7、g7—直接和参数激励项系数；k8—等效重力；γ1、γ2—等效机电耦合系数。方程中谐波激励：

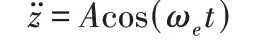
式中：A—外部加速度激励幅值；ωe—外部激励圆频率，Ω=ωe/（2π）。

根据式（11）可知，梁1和梁2的固有频率f1和f2分别为：

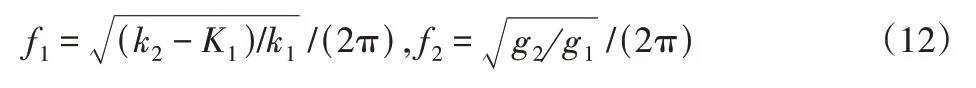
为了对比参数激励单梁压电俘能器和磁力T型压电俘能器的俘能特性，将梁1及质量块M2去除，将梁2直接与激振器连接，则得到文献[4]所提出的参数激励单梁压电俘能器。此时，将式（11）中的第二个方程含X的耦合项舍去，则可以得到参数激励单梁压电俘能器的动力学方程为：

式中：YS和VS—在没有附加梁1时，梁2—单梁时的位移响应和输出电压。根据文献[11]，俘能器的俘能效果可采用平均输出功率为评价指标，计算式：

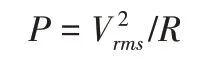
式中：Vrms—均方根电压。

当负载电阻R为定值时，平均输出功率与均方根电压的平方成正比，因而，均方根电压Vrms也可作为俘能效果的一个指标。

3 磁力T型压电俘能器的特性分析

数值仿真时，利用MATLAB对式（11）和式（13）进行求解，若没有特别说明，初始值都取0，负载电阻R取1MΩ。

磁力T型压电俘能器的参数，如表1和表2所示。

表1 磁力T型压电俘能器材料参数Tab.1 Material Parameters of Magnetic T-Shaped Piezoelectric Energy Harvester

表2 磁力T型压电俘能器结构参数Tab.2 Structural Parameters of Magnetic T-Shaped Piezoelectric Energy Harvester

3.1 参数激励单梁俘能器的俘能特性

参数激励下单梁压电梁2的特性，如图3所示。

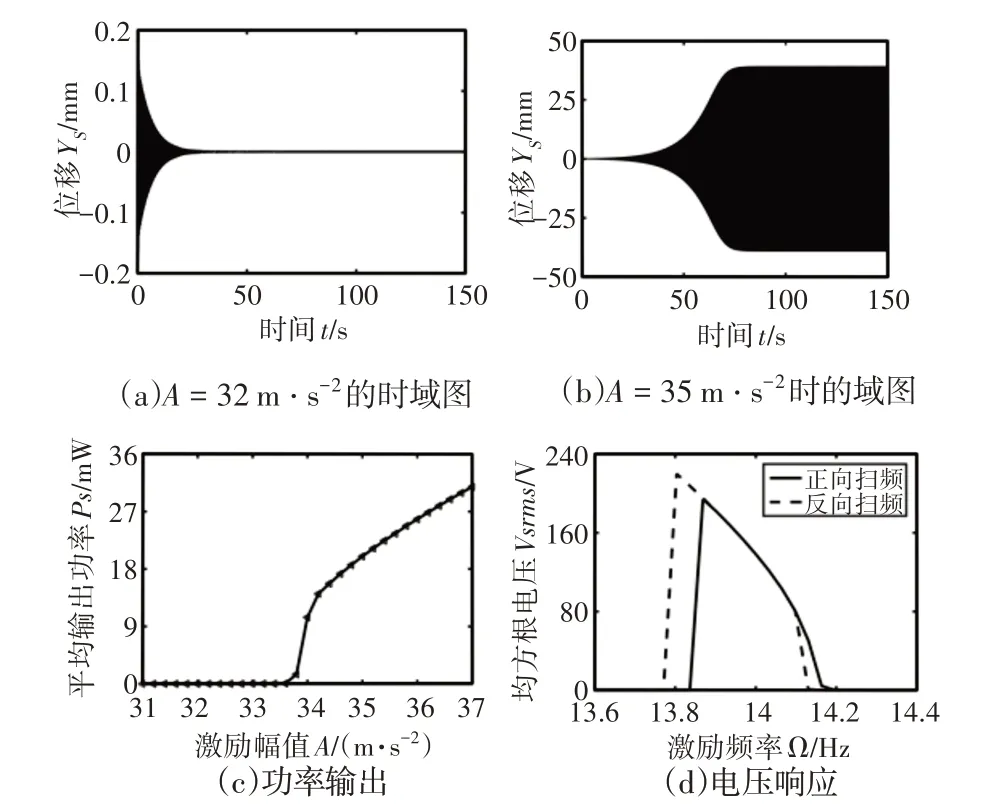
图3 参数激励单梁梁2的运动及俘能特性Fig.3 Motion and Energy Harvesting Characteristics of Beam 2 Under Parametric Excitation

参数激励单梁俘能器的结构中没有梁1和质量块M2，其动力学方程，如式（13）所示。

根据表中的参数可以得知梁2的固有频率为6.95Hz，在仿真时，取激励频率约为梁2的2倍固有频率，即Ω=14Hz。

对于参数激励单自由度系统，初始值不能取为0，因此初始值取[0.01，0，0]。

激励幅值为32m·s−2和35m·s−2时梁2的时域图，图3（a）和图3（b）所示。可以看出当激励幅值为32m·s−2，系统稳定的动态响应趋于0；而当激励幅值为35m·s−2，系统具有稳定的运动。图3（c）表明；当激励幅值为35m·s−2时，梁2有明显的功率输出，即系统的激励阈值为33.6m·s−2。

图3（d）表明；当激励幅值为33.6m·s−2，并且梁2 在其固有频率的2 倍处（14Hz）发生主参数共振时，反向扫频带宽略宽于正向扫；梁2振动带宽，即俘能器的俘能带宽小于0.4Hz。

3.2 磁力T型压电俘能器的俘能特性

3.2.1 磁铁间距d0与系统的固有频率

这里主要是利用调整磁铁间距d0，改变作用于梁1末端质量块M1的受力，从而改变梁1的固有频率，达到产生共振的频率条件f1=2f2。

按照式（12）可以计算出对应不同磁铁间距d0，梁1的固有频率f1、梁2的固有频率f2以及他们之间的关系，如图4所示。

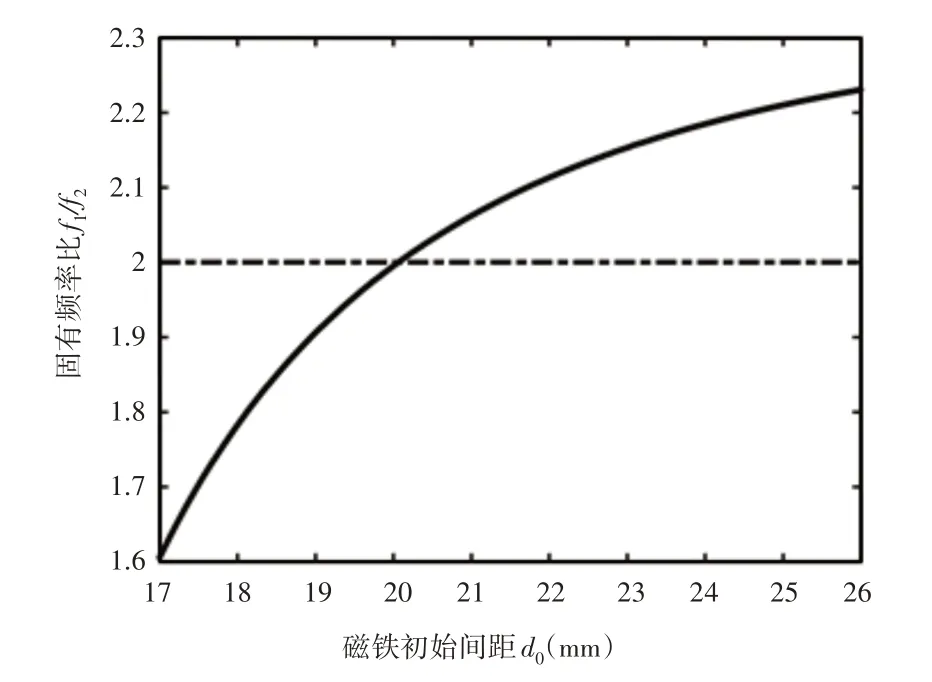
图4 磁铁间距与梁的固有频率之间的关系Fig.4 Relationship Between Magnet Distance and Natural Frequency of Beam

从图4中可见，随着d0的减小，梁1的固有频率f1与梁2的固有频率f2之比将单调地减小，当d0=20mm 时，梁2的固有频率为6.95Hz，梁1的固有频率约为14Hz，即梁1的固有频率约为梁2的固有频率的2倍。

如果假设梁1末端没有磁力作用，d0无穷大时，则f1≈2.36f2，说明采用这里的系统参数，固有频率比的极限值是2.36。

3.2.2 不同固有频率比的系统频率响应

随着磁铁间距d0的变化，梁1的固有频率f1将发生变化，与梁2的固有频率f2之比也随之发生变化，因而系统的动态响应也会发生变化。

图5（a）、图5（b）所示分别为激励幅值A=5m·s−2时，梁1和梁2的频率响应。

从图5（a）可以看出；当d0为无穷大时，频率响应曲线与线性振动类似，说明此时系统中磁力非线性因素的影响比较小；随着d0的减小，梁的固有频率比逐渐减小，梁1的振幅逐渐减小，当d0=20mm和d0=18mm时，出现了双峰；在此之后，继续减小d0时，梁1的振幅又逐渐增大，而且频率响应曲线峰值的右侧出现了明显的突变，意味着出现了跳跃现象，表现为硬弹簧特性，说明磁力非线性因素的影响增大。

从图5（b）可以看出；梁2的电压响应也表现出类似的特性。在固有频率比大于2而小于2.36的范围内，随着d0的减小，频率响应的硬弹簧特性逐渐减弱，软弹簧特性逐渐增强，当d0=20mm和d0=18mm时，出现了双峰；在固有频率比小于2的范围内，减小d0，将导致硬弹簧特性彻底消失，只表现出软弹簧特性，形成单一峰值的左侧出现跳跃现象。

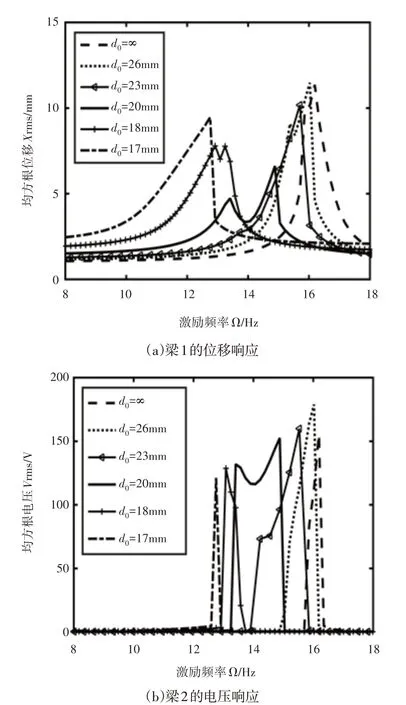
图5 磁铁间距对频率响应的影响Fig.5 Influence of Magnet Distance on Frequency Response

就系统的俘能性能而言，随着d0的减小，梁2频率响应的最大均方根电压也进一步减小，而梁2的带宽则表现出先增加后减小的趋势，其转折点出现在d0=20mm附近，即f1≈2f2。此时，系统发生了1；2的内共振。

3.2.3 系统内共振时的动力及俘能特性

当d0=20mm 时，梁1的固有频率f1与梁2的固有频率f2之间满足f1≈2f2，则系统发生1；2的内共振。激励频率为14Hz时，系统随激励幅值的响应，如图6所示。

从图6（a）可以看出；当激励幅值小于0.5m·s−2时，梁1的均方根位移随激励幅值的增大而增大，但当激励幅值大于0.5m·s−2时，梁1的均方根位移基本保持不变。这是由于1；2内共振而发生了饱和现象，梁1的能量传递给了梁2。

从图6（b）可以看出；磁力T型压电俘能器系统的激励阈值为0.5m·s−2，相比于2.1节中参数激励单梁俘能器的阈值33.6m·s−2，得到了很大程度的减小。

由图6（c）、图6（d）所示梁1和梁2位移的时域图可见；系统在激励幅值为0.6m·s−2时梁2能发生参数共振，梁1的位移在运动约30s之后变小并在此之后又保持不变，说明了系统的确发生了饱和现象。

图6 磁力T型压电俘能器的俘能特性Fig.6 Characteristics of Magnetic T−Shaped Piezoelectric Harvester

当激励幅值为A=3m·s−2，磁铁间距d0=20mm 时，系统的正向和反向扫频时的频率响应，如图7所示。

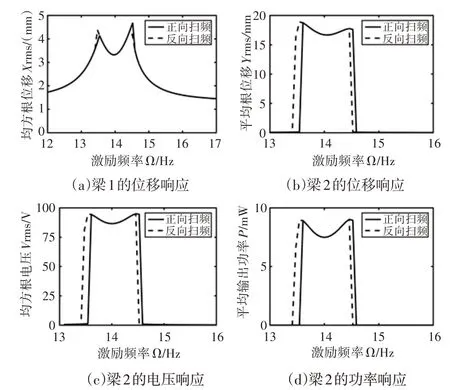
图7 磁力T型压电俘能器频率响应Fig.7 Frequency Response of Magnetic T−Shaped Piezoelectric Energy Harvester

从图7（a）可以看出；梁1的频率响应出现了双峰，从图7（b）～图7（d）可以看出，梁2的频率响应既有软弹簧特性，也有硬弹簧特性，表现出双跳跃现象[12]，并且由于参数共振，响应曲线较为平坦。虽然正向和反向扫频频率响应略有差异，但梁2的电压响应带宽均约为0.9Hz，已经比参数激励单梁俘能器的0.4Hz提高了125%。

当d0=20mm时，随着激励幅值的增大，磁力T型压电俘能器均方根电压的频率响应，如图8所示。

从图8可见；随着激励幅值的增大，系统输出的均方根电压增大，频率响应带宽也会增加；并且频率响应曲线向右弯曲的部分更多，表现出更强的硬弹簧特性，当激励幅值为9m ⋅s−2时，带宽可以增加到3Hz。

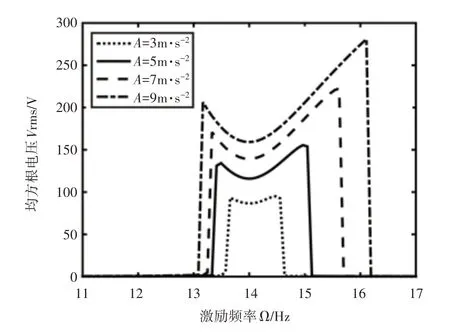
图8 激励幅值对系统频率响应的影响Fig.8 Influence of Excitation Amplitude on Frequency Response of System

4 结论

这里提出了一种磁力T型压电俘能器，通过调节磁铁间距d0使系统固有频率满足f1≈2f2时，不仅能在很大程度上降低发生参数共振的激励阈值，并且由于结合了软硬弹簧特性，频率响应带宽提升100%以上。

研究表明：（1）梁1在主参数共振频率处发生了饱和现象，其振幅不受激励幅值的影响，在远离主参数共振频率处，其振幅随着激励幅值的增大而增大。增大激励幅值不仅能增加梁2的电压输出，同时也能增大频率带宽。（2）随着磁铁距离d0的减小，梁2的带宽表现出先增大后减小的趋势。当d0满足使系统的固有频率之比近似满足f1≈2f2时，系统的频率响应的带宽达到最大。

最后，这里得到的数值仿真的结论，可作为系统设计的依据和参考。未来的工作包括对系统的参数进行优化，使系统能在较低的激励幅值下产生更宽的频率响应；另外，当减小磁铁间距使梁1变为屈曲梁时，系统的俘能特性也是值得研究的课题。