基于Flink的k-支配skyline体并行求解算法*

孙国璋，黄 山，艾力卡木·再比布拉，徐浩桐，段晓东

(1.大连民族大学计算机科学与工程学院，辽宁 大连 116600;2.大数据应用技术国家民委重点实验室(大连民族大学)，辽宁 大连116600;3.大连市民族文化数字技术重点实验室(大连民族大学)，辽宁 大连116600)

1 引言

Skyline查询在多目标决策、数据可视化等领域有着广泛的应用。自2001年Borzsonyi等人[1]将其引入到数据库中以来，skyline查询受到了众多研究人员的关注,并取得了一系列研究成果。现有skyline查询及其变体可以解决大部分实际问题，并且能够在大规模数据集中得到有效信息。

Skyline查询可以筛选掉部分无用数据，但是随着数据规模和维度的增长，数据点之间的支配可能性会变得非常小，导致结果集中存在大量的数据点，数据点规模甚至接近于原数据集的规模，这使得用户无法快速从结果集中获取到有价值的数据。为了解决上述问题，Chan等人[2]提出了k-支配skyline的概念，它将支配的概念放宽到k-支配，以提高数据点之间的支配可能性，使得结果集的规模变得足够小，足以让用户能从中筛选到有价值的数据。

为了进一步提高算法效率，Yuan等人[3]提出了共享策略，以解决每个skyline查询独立计算导致的效率低下问题。但是，该策略只适用于传统skyline查询算法，不能直接用于k-支配skyline算法。随着k-支配概念的提出，董雷刚等人[4]便在k-支配skyline查询中引入共享策略，提出了基于共享策略的k-支配skyline体的算法。该算法通过k-支配skyline体的计算可以得到任意k值对应的k-支配skyline。但是，该算法需要重复利用初始数据集对数据点进行支配性检查，影响了算法的查询效率。而现有的k-支配skyline算法主要是面向于单用户设计的，无法有效地解决多用户查询问题。

针对上述问题，本文首先提出了一种面向多用户的k-支配skyline体求解优化算法，然后基于该算法提出了一种运行在并行处理框架Apache Flink上的k-支配skyline并行求解算法，有效解决了多用户查询问题，实现了高效、高吞吐量的查询处理。本文主要工作如下所示：

(1)提出了面向多用户的k-支配skyline体求解优化算法MKSSOA(Multi-user K-dominated Skyline Solving Optimization Algorithm)，利用每名用户的结果集和中间集进行存储和共享，在支配检查过程中，根据当前用户2个集合中数据点出现的先后次序对候选集进行二次筛选，以减少数据点之间的比较次数。

(2)在MKSSOA算法的基础上，提出了面向多用户的k-支配skyline并行求解算法MKSPSA(Multi-user K-dominated Skyline Parallel Solving Algorithm)，通过利用并行处理框架Apahce Flink的自身优势和算子特性来调度不同算子间的数据进行并行计算，进一步提高了算法执行效率。

(3)在合成数据集和真实数据集上进行了系统的实验研究，验证了本文算法的有效性、高效性和可扩展性。

本文第1节介绍了skyline查询和k-支配skyline查询的相关方法和研究现状；第2节介绍了本文所需的相关概念及定理；第3节介绍了k-支配skyline体并行求解算法；第4节通过对比实验验证了所提算法的有效性；第5节总结了本文的工作。

2 相关工作

自从k-支配概念[2]和相关查询算法提出后，国内外研究人员在k-支配skyline查询问题上取得了一系列研究成果，主要分为如下几个方面：

(1)考虑到数据排序和索引结构对查询效率的影响，Siddique等人[5]提出了一种使用排序过滤方法的k-支配skyline算法;印鉴等人[6]通过为数据集建立2个索引，减少了数据点之间的比较次数，提高了算法执行效率。Siddique等人[7]提出了一种根据数据点的支配能力指数进行排序的k-支配skyline算法。黄荣跃等人[8]为了减少预排序的时间开销，提出了一种预排序k-支配skyline查询算法。Siddique等人[9]提出了一种统计数据点支配能力的方式处理高维数据集的k-支配skyline算法。吴俊杰等人[10]通过skyline层次计算元组支配能力并提出了k支配能力排序skyline查询算法。黄金晶等人[11]提出了一种 k*-支配 skyline 算法，在支配关系中引入用户偏好的优先级，控制结果集规模的同时又消除了循环支配的可能。

(2)在分布式环境下，Tian等人[12]提出了一种基于点的绑定树PB-Tree(Point-based Bound tree)的k-支配skyline查询算法，该算法利用PB-Tree分割数据空间并在每个子空间独立计算k-支配 skyline，最后再使用MapReduce进行并行计算。Peng等人[13]提出了一种引入特征位图来验证支配和k-支配关系的并行k-支配skyline算法。Siddique等人[14]提出了一种在MapReduce环境下使用OB-Tree(Object-based Bound Tree)来划分数据空间进行k-支配skyline的算法。Ding等人[15]提出了一种在MapReduce环境中基于支配的分层树的索引结构并实现了其构造算法。Ding等人[16]提出了一种针对不完整数据的支配层次树的索引结构并结合MapReduce计算框架实现了有效的查询算法。

(3)针对特殊数据集和不同应用环境，Kontaki等人[17]提出了一种在多维数据流上连续进行k-支配skyline算法。Siddique等人[18,19]提出了一种基于分而治之的k-支配skyline算法，以解决数据库频繁更新的问题。Dong等人[20]提出了一种解决多个数据集的 k-支配skyline算法。Miao等人[21]提出在不完整数据下进行k-支配skyline算法并扩展了加权支配skyline查询和top-k支配查询算法，以适应不完整数据。廖再飞等人[22]提出了一种面向不完整数据流的k-支配skyline算法。Lai等人[23]提出了一种在不确定数据流下通过中间索引提高更新率的k-支配skyline算法。Li等人[24]提出了一种基于支配能力的并行不确定k-支配skyline查询方法。Awasthi等人[25]提出了一种通过扩展k-支配 skyline查询来处理连接关系的算法。李松等人[26]提出了一种道路网环境下的k-支配空间skyline算法。Tripathy等人[27]提出了在动态环境下计算k-支配skyline的查询算法。Zheng等人[28]提出了一种根据支配能力处理动态数据集的k-支配skyline查询算法，且解决了频繁更新数据库的维护问题。

Dong等人[4]提出了基于共享策略的k-支配skyline算法，该算法通过减少部分冗余操作，节约检查支配的时间，解决了不同k之间结果的共享问题。但是，该算法每次筛选下一个k-支配时都使用原数据进行比较，增加了时间消耗。董雷刚等人[29]提出了一种针对k值动态变化的k-支配skyline算法，该算法以现有查询结果为基础，通过变化的k值重新判断数据点，进而得到新的查询结果。不过，在数据点不能被自身数据集中的数据点所支配时，仍需要再次对非自身数据集中剩下的数据点进行支配检查，这使得算法的效率较低。

综上所述，现有的k-支配skyline查询算法一般都是针对单用户查询，但查询用户往往是不唯一的，在出现多名查询用户时，需要重复运行查询算法，这会导致算法产生额外开销。同时，对于以往引入共享策略和更新k-支配的相关研究，也不能很好地处理多用户查询问题，同样也不适用于在并行处理框架上进行k-支配skyline查询，具有一定的局限性。

3 相关概念及定理

给定一个d维空间S={s1,s2,s3,…,sd}，如果每一个点pi∈D是S上的一个d维数据点，则可以称集合D={p1,p2,p3,…,pn}是S上的数据集。此外，用pi.sj表示数据点pi第j维的数值。

定义1(支配(dominate)[1]) 点pi在空间S上支配pj，当且仅当∀sk∈S，pi.sk≥pj.sk且∃st∈S，pi.st>pj.st。

定义2(k-支配(k-dominate)[2]) 点pi在空间S上k-支配pj，当且仅当∃S′⊆S，|S′|=k，∀sr∈S′，pi.sr≥pj.sr且∃st∈S′，pi.st≥pj.st。

定义3(k-支配skyline(k-dominant skyline)[2]) 点pi是 k-支配 skyline 点，当且仅当不存在任何一点满足pj∈D且pj≠pi的条件使得点pjk-支配点pi。

本文用DSP(k,D,S)表示在空间S上数据集D的所有k-支配skyline点集。

当k=d时，定义2中所提到的k-支配关系等同于定义1中的传统支配关系。

引理1对于任意2点pi，pj∈D，如果点pi(k+1)-支配pj，那么pi一定k-支配pj[2]。

推论1|DSP(k,D,S)| ≤ |DSP(k+1,D,S)|[2]。

定理2如果k<(d+2)/2，则任何一对k-支配skyline点至少在d-2k+2维度上具有相同的数值[2]。

从推论1中可知，k-支配skyline数据点的数量会随着参数k的变小而单调递减。因此，选择一个合适的k值可以将k-支配skyline的数据点控制在一定范围内，但是参数k的取值必须考虑实际意义，不能一味地降低。根据定理2可知，除非数据集中存在大量至少在d-2k+2维度上数值相同的数据点，才有必要将k的取值控制在(d+2)/2之下；否则会导致结果集中数据点的数量急剧减少，甚至出现空集的情况，进而失去管理和分析的意义。

定义4(k-支配skyline体(k-dominant skyline cube)[4]) 在d维空间中进行k-支配skyline查询，最多有d种不同的k-支配skyline结果，所有k-支配skyline的集合为k-支配skyline体，记作k-SKYCUB(D,S)。

定义5(多用户k-支配skyline体(Multi-user k-dominant skyline cube)) 在d维空间中进行k-支配skyline查询，最多有d种不同的k-支配skyline结果，由于多用户的不确定性和合理性，参数k的取值应在大于或等于(d+2)/2和小于d的范围内。如果参数k取到小于(d+2)/2的数值，至少需要在d-2k+2维度上有相同的数值，由于这种情况发生的概率很小，故不做考虑。因此，在k值的取值范围内，最多有(d-2)/2种k-支配skyline结果，将其称为多用户k-支配查询，记作MKDSC(u,D,S),其中u表示用户数量。

下面通过实例来说明k-支配skyline和多用户k-支配skyline体。

当3名用户在同一时间内进行k-支配skyline查询时，这3名用户会因为参数k的取值分为多种情况，其中最好的情况是每名用户取相同的k值进行查询，最差的情况则是每名用户的k值均不相同。

以表1(左)为例，当3名用户全部将k值设为6时，只需从表2所示的数据集中进行一次6-支配skyline查询即可，从而避免了3名用户的重复查询，最终得到的结果为{p2,p5}；以表2(右)为例，当3名用户的k值均不相同时，用户A在计算7-支配skyline查询后得到的结果集为{p1,p2,p4,p5}，然后用户B根据用户A的结果集进行6-支配skyline查询，得到的结果集为{p2,p5}，同样，用户C将用户B的结果集作为其初始数据集进行5-支配skyline查询，得到的结果集为{p2}。

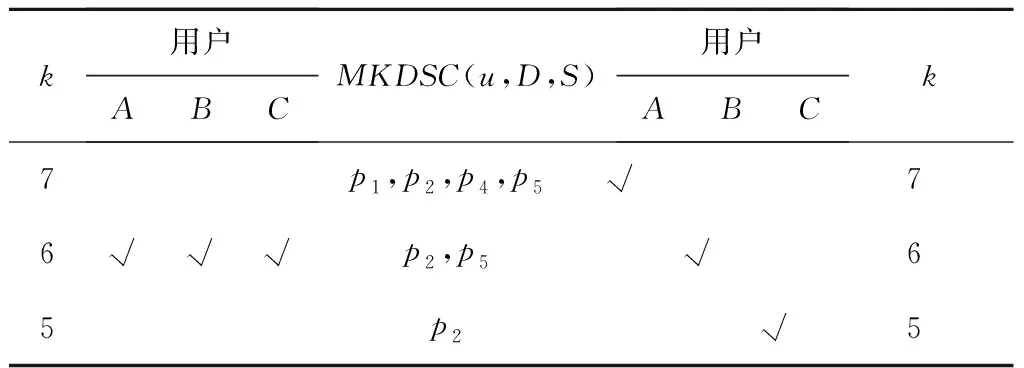
Table 1 Best case (left) and worst case (right) for the three user queries

4 k-支配skyline体并行求解算法

本节首先介绍k-支配skyline体求解优化算法MKSSOA，随后在MKSSOA算法的基础上，提出一种引入并行处理框架Apache Flink的k-支配skyline体并行求解算法MKSPSA，该算法利用Flink并行化和算子特性，进一步提高了算法效率。

4.1 k-支配skyline体求解优化算法

对于k-支配skyline算法的查询思想，有如下2个性质需要用到：

假设数据点p∈D且不是一个k-支配skyline点，则有以下性质[2]：

性质1数据集D中必定存在一个传统skyline k-支配数据点p。

性质2数据点p有可能不被任意k-支配skyline点所k-支配。

定理3对于数据集D和某用户的结果集R，若其他用户的k′小于该用户的k，则选择最接近k的k′用户，利用结果集R代替数据集D进行k′-支配skyline查询，即对结果集R中的数据点重新进行支配比较，从而得出新的结果R′。

证明根据定理1和推论1可知，随着k值减小，结果集R中数据点的数量也有可能会变少，因为结果集R中的数据点可能会被其他点所支配，因此需要对结果集R中的数据点重新进行支配判断，根据性质2可知，结果集R中的数据点还需要被中间集T中的数据点进行支配判断，进而可以保证结果的准确性。

定理4通过之前用户i的中间集Ti分别对当前用户候选集R进行支配检查时，需要将从候选集R中移除的数据点加入到当前用户自己的中间集T中，进而提升算法的查询效率。

证明用反证法。如果将候选集R中移除的数据点加入到其他用户i的中间集Ti中，在k-支配检查过程中，其他用户的中间集Ti会再次与当前用户的候选集R进行比较，这意味着数据间的比较次数将会增加，进而降低查询效率。

Table 3 Symbols definition in algorithm

根据上述性质和定理，本文将优化算法分为3个主要过程：查询过程，k-支配检查过程和数据传递过程。以表1中的数据集D为例，3名用户以最差情况进行k-支配skyline查询。当k=7时，用户A的结果集为{p1,p2,p4,p5}，中间集则为{p3,p6}，接下来用户B利用用户A的结果集进行6-支配skyline查询，得到自己的候选集{p2,p5}和中间集{p4,p1}。而在文献[4]中，用户B的结果集需要对用户A的结果集与数据集D中的数据点进行依次比较才可得到，这样会导致数据点间重复计算。在保证结果准确的前提下，本文在k-支配检查过程中进行了优化，本文只需要根据数据点的前后次序进行比较。以用户B结果集中的点P2为例，该点需要与{p3,p6}进行比较，因为它们之间并没有进行过5-支配计算。接着再与{p1,p4}中的{p1}进行比较，因为在查询过程中，p2和p4已经完成了5-支配比较。基于此，本文算法的比较次数会比文献[4]的少，进而算法执行效率会更高。最后，用户C将用户B的结果集作为其初始数据集进行5-支配skyline查询，得到候选集{p2}，紧接着进行k-支配检查，得到结果集{p2}。这样将上一名用户的结果集作为当前用户的数据集进行k-支配查询的做法加快了多名用户整体的查询时间。

算法1描述了上述过程的具体细节，算法中的符号定义如表3所示。第①行代码表示需要从多用户k-支配查询集中取出最大k值。第②行代码用一个子算法来处理数据集D，该过程在算法2中进行了详细描述。第③行代码表示在另一个子算法中，利用多个中间集T检查候选集R中非k-支配skyline点，该子算法在算法3中进行了详细描述。第④行代码表示将候选集R传递给下一位用户作为其初始数据集，便可再次执行总流程直到查询完所有用户，进而得到多个用户的k-支配skyline查询的结果集。

算法1k-支配skyline体求解优化算法(MKSSOA)

输入：数据集D，多用户k-支配查询集K。

输出：Ru,…,R1。

①forevery userk∈Kdo

②Ri,Ti←getKdSetAndNotKdSet(D,Ri,k)；

③Ri←getResult(Ri,Tu,…,Ti)；

④Ri+1=Ri；

⑤endfor

⑥returnRu,…,R1

算法2为查询过程，将数据集D中的每个数据点与候选集Ri中的数据点逐一比较，如果点p被点p′所k-支配，那么数据点p将会加入中间集Ti中，否则加入候选集Ri中；如果点p′被点p所k-支配，那么点p′将会存到中间集Ti并从Ri中移除。根据性质2，在第1次扫描结束后，候选集Ri中会存在非k-支配skyline的数据点，因此需要进行k-支配检查，以消除候选集中的非k-支配skyline点。

算法2getKdSetAndNotKdSet(D,Ri,k)

输入：数据集D，候选集Ri，用户的支配维度k。

输出：Ri,Ti。

①forevery pointp∈Ddo

②flag=1；

③forevery pointp′∈Rido

④ifp′ k-dominantpthen

⑤flag=0；

⑥endif

⑦ifpk-dominantp′then

⑧ insertp′intoTi;

⑨ removep′fromRi;

⑩endif

算法3为k-支配检查过程，需要将用户候选集Ri中的点与之前所有用户的中间集和自身中间集当中的点进行比较，如果数据点p被数据点q所k-支配，那么将点p从Ri中移除并添加到中间集中；但是当与自身中间集中的点进行比较时，只需将点p与自身中间集中比点p早出现却被加入到自身中间集中的数据点进行比较，因为比点p晚出现的点都已经在查询过程中完成了比较。因此，该过程减少了不必要的重复比较且可以得到更加准确的结果.

算法3getResultSet(Ri,Tu,…,Ti)

输入：对应用户的候选集Ri,中间集Tu,…,Ti。

输出：Ri。

①forevery pointq∈{Tu,…,Ti}do

②forevery pointp∈Rido

③ifu=ithen

④ifqearlier thanpthen

⑤ifqk-dominatepthen

⑥ insertpintoTi;

⑦ removepfromRi;

⑧endif

⑨endif

⑩else

4.2 k-支配skyline体并行求解算法

Apache Flink 是新一代的分布式并行处理框架，已被广泛运用于大数据计算中，数据处理过程见图1。Apache Flink能在所有常见集群环境中运行，可以对任意规模的数据进行快速计算，它需要计算资源来执行应用程序并且能以内存速度和任意规模进行计算。

Figure 1 Data processing of Flink图1 Flink的数据处理过程

由于目前Apache Flink 的版本默认采用Pipelined Region Strategy 调度策略，Pipelined 就会在上下游节点进行数据交换，即上游边写，下游边读边消费。这样能够节省调度花费的时间，对上下游任务进行并行处理，减少了线程之间的缓冲和切换开销，同时也避免了不必要的资源浪费，提高了整体吞吐量。因此，本文利用该特性对查询算法进行并行化处理。

图2展示了多用户k-支配skyline最终结果的计算过程。首先，通过map算子对数据集进行处理并将数据流发送给下游的算子节点；然后，flatmap算子在接收到数据后，开始进行k-支配skyline查询。以表1为例，当k=7时数据集会分为2部分：候选集R和中间集T，接着数据流传输到下一个flatmap算子当中，该算子可以对每个k值相同的候选集和中间集分组，同时包含大于当前k值的中间集。此时，k=7的用户便可得到正确的结果集。然后将数据流重新发送到flatmap算子进行下一名用户的k-支配skyline查询，紧接着进行flatmap操作分组，重复多次上述操作，直到最后一名用户完成查询，最后所有用户的查询结果组成多用户k-支配结果集。

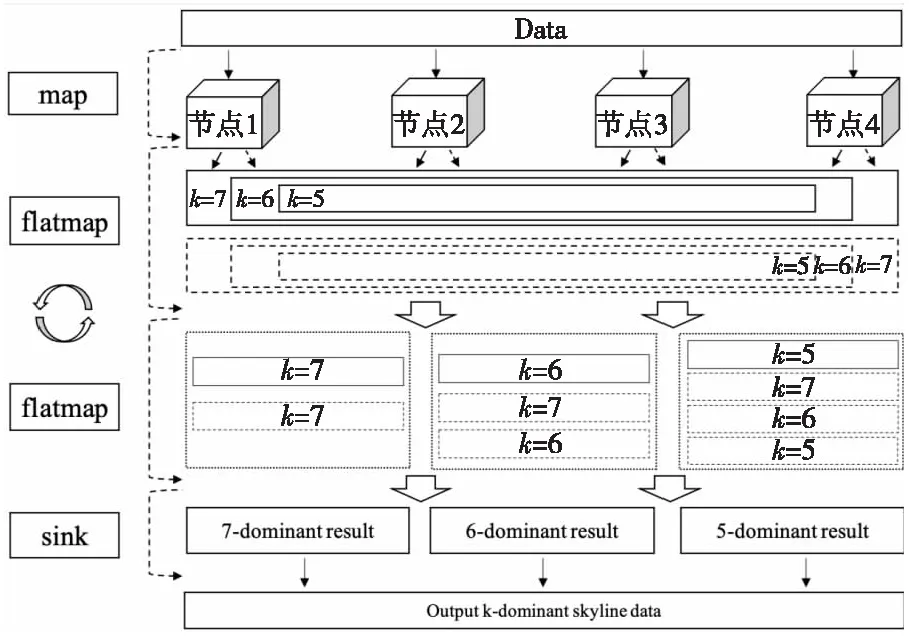
Figure 2 Calculate processing of final results图2 最终结果计算过程

算法4表示在集群上的运行过程。第①行代码为获取Flink执行环境。该环境记录了用户作业和集群配置等信息，默认情况下系统会自动检测节点硬件环境并进行配置。由于算子层次的并行度优先级高于系统层次、客户端层次和执行环境层次，因此该算法在算子层次上设置并行度。这种设置不仅方便调试，还可以为多个算子设置不同的并行度。第②～③行代码表示从文件中读取数据集并在读取到的数据上做map操作，以转换input并存储数据。第④～⑩代码行是对多用户中的每名用户逐一进行flatmap、flatmap操作、设置并行度和传递数据集。首先，第1个flatmap算子调用算法2和算法3完成查询过程和k-支配检查过程，得到用户的结果集R和中间集T。接着第2个flatmap算子对当前用户的结果集R和多名用户的中间集T进行分组;然后，为算子设置相应的并行度;最后，将用户的结果集传递给下一名用户,并作为其初始数据集。第～行代码表示在输出所有用户的k-支配skyline数据后，将作业提交给集群执行，直到作业执行完毕，返回作业执行结果。

算法4k-支配skyline体并行求解算法(MKSPSA)

输入：数据集D，多用户k-支配查询集K。

输出：Ru,…,R1。

①env←getExecutionEnvironment();

②inputs←env.readFile(D);

③Data←input.map(newMapFunction);

④forevery userk∈Kdo

⑤Ri=Data;/*只为第1个用户执行1次*/

⑥Ri→flatMap()；/*调用算法2和算法3，得到结果集R和中间集T*/

⑦ →flatMap()；/*将当前用户的结果集R和多名用户中间集T进行分组*/

⑧ →setParallelism();/*设置算子并行度*/

⑨Ri+1=Ri;/*将上一个用户的结果集传递给下一名用户，并作为其初始数据集*/

⑩endfor

5 实验评估

5.1 实验环境与数据集

本文的单机实验环境为Intel Core i7-8700 3.2 GHz CPU，32 GB内存，CentOS 7操作系统，1.12.4版本的Flink。集群实验环境由9台高速千兆网络连接的PC机组成，每台PC机的配置为Intel Core i7-8700 3.2 GHz CPU，32 GB内存，操作系统为CentOS 7，其中1台PC机为Master节点，其它PC机为Slave节点，Master节点仅作为JobManager，Slave节点作为TaskManager独享使用，同时每个TaskManager设置6个Slot，Flink版本为1.12.4.

实验数据由合成数据集和真实数据集2部分组成。真实数据集来自NBA球员从1950赛季到2017赛季所有的表现统计，不限于得分、篮板、助攻、抢断等低阶数据，还包括有效命中率、真实命中率、篮板率等高阶数据，共45项技术统计，数据集共有 24 624条数据点。合成数据集是采用文献[1]中的生成工具生成的相同维度不同数据量的数据集和不同维度相同数据量的数据集。数据量在5万条～25万条变化，默认维度是50。数据集维度的变化区间在50～100，默认数据量为5万条数据。一般情况下，测试k-支配skyline查询性能需要分别从相关分布、反相关分布和独立分布的数据集进行测试。

相关分布是指如果数据点在某一维度上的值比较好，那么该点在其它维度上的值同样会比较好，因此相关分布的数据之间容易产生支配关系，得到的skyline点集会很少。

反相关分布是指如果数据点在某一维度上的值比较好，那么该点在其它维度上的值反而比较差，因此，反相关分布的数据之间不容易产生支配关系，得到的skyline点集会很多。

独立分布是指每个数据点是随机生成的，它们各维度上的值都是相互独立的且不会相互影响。

在对比算法方面，选择了基于共享策略的k-支配skyline算法TBA(Top-Bottom Algorithm)[4]。该算法通过共享策略可以实现类似多用户k-支配skyline查询的效果；其次选择了具有更新k-支配轮廓特性的BT[29]算法。该算法中k值动态变化的形式与本文算法相同。TBA[4]和BT[29]算法同本文算法(MKSSOA)在单机实验环境下进行测试对比，同时将MKSSOA算法与在集群环境下提出的MKSPSA算法进行对比实验。在结果准确性一致的前提下，选择算法执行时间作为评价指标。

5.2 实验结果与分析

图3测试的是关于数据量变化对算法查询效率的影响。设数据集维度为50，数据量在5万条～25万条变化，5名用户在最差情况下测试了3种查询算法的查询性能。

Figure 3 Effect of data volumes on algorithm query performance图3 数据量对算法查询性能的影响

从图3中的实验结果可以看出，随着数据量的增加，算法的查询时间也随之增加，这是由于数据点之间的比较次数增加，导致算法执行效率降低。由图3a和图3b可知，MKSSOA算法与TBA算法和BT算法的执行时间相差不大。因为在反相关数据集中，数据点之间较难产生支配关系，比较次数大致相同，所以3种算法的时间消耗相差不明显。而在相关数据集中，数据点之间容易产生互相支配的关系，算法执行时间相比反相关数据集会下降很多，不过3种算法在运算过程中数据集中的数据点的比较次数相差不大，故三者执行时间呈大致相同的变化趋势且区别不大。从图3c可以看出，MKSSOA算法在时间消耗上有较为明显的下降。这是因为在k-支配检查过程中，用户候选集和中间集中存在大量不需要比较的数据点，数据点之间的比较次数减少，进而加快了算法查询速率。

图4测试的是数据维度变化对算法查询效率的影响。设数据量为5万条，数据维度在50～100变化，5名用户在最差情况下对3种查询算法的性能进行测试。

Figure 4 Effect of dataset dimensionality on algorithm query performance图4 数据集维度对算法查询性能的影响

从图4可以看出，随着数据集维度的增大，3种算法的测试结果变化曲线相差不大，但是可以明显看出，MKSSOA算法在独立分布上的效率优于另外2种算法的。在反相关分布和相关分布的数据集中，3种算法的执行时间较为相近，而在独立分布的数据集中，MKSSOA算法对候选集和中间集分别进行了存储，在k-支配检查过程中，根据候选集和中间集中数据点出现的先后次序，避免了大量数据点之间的重复计算。因此，在数据集维度增加的情况下，MKSSOA算法优于TBA算法和BT算法，具有更好的查询效率。

为了验证MKSSOA算法是否适用于真实数据集，选取NBA球员在每个赛季的技术统计数据集进行验证。因为在NBA联盟中球队经理需要权衡多项技术统计来交易或选择球员，所以选择NBA球员技术统计数据集是有意义的。

图5是测试不同初始维度对算法的查询性能的影响。由于NBA球员数据集的维度为45，当k值选择过大或者过小都会对结果产生影响，选择过大会产生过多的结果且不具有查询意义，选择过小则失去了筛选的目的，因此模拟5名用户在最差的情况下分别以初始维度为28，34和40进行向下查询。

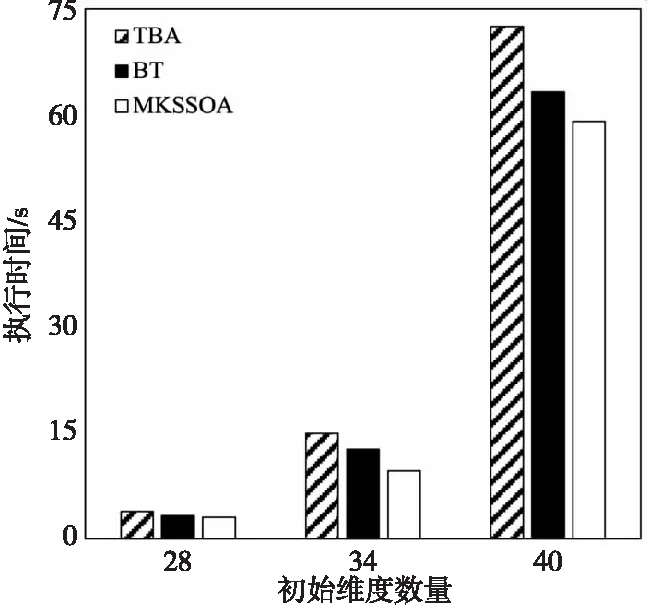
Figure 5 Effect of different initial dimensions on algorithm query performance图5 不同初始维度对算法查询性能的影响

从图5可以看出，MKSSOA算法在执行时间方面优于TBA算法和BT算法。这主要是因为随着数据集维度的增加，数据点之间支配关系变得复杂，而MKSSOA算法对候选集、中间集分别存储后，可以有效利用中间集中的数据点进行支配检查，相较于另外2种算法，减少了数据点间因复杂的支配关系引发的重复计算问题。由于上述比较算法无法在集群环境进行测试，因此本文选择MKSSOA算法与MKSPSA算法以准确度为评价指标对算法执行效率进行测试。首先，测试了MKSPSA算法在不同并行度下的效率；然后，在最佳并行度的基础上分别对独立分布数据集和真实数据集进行了测试。

如图6所示，实验测试了不同并行度对算法执行时间的影响。独立分布数据集的数据量为5万条，数据维度为50，5名用户在最差情况下在该数据集上进行查询操作。为了排除其它因素的影响，确保实验的准确性，本文通过多次测试取平均值的方法确定最终结果。从图6可以看出，随着并行度的逐渐增加，算法执行时间会先下降到一定程度，随后呈现出小幅上升并再次下降的变化趋势。这是由Apache Flink内部机制导致的，并行度的提高并不一定能提升处理能力，只有控制好每个任务管理器(TaskManager)上子任务 (subtask)的数量，才能避免多余的subtask成为整个任务的瓶颈。为了减少subtask的限制数量和避免资源浪费，本文将subtask设置成2的整数次幂。从实验结果可以看出，并行度为32的算法执行时间最低，因此在后续的集群环境下均将并行度设置为32进行实验测试。

Figure 6 Effect of different parallelism degrees on algorithm query performance图6 不同并行度对算法查询性能的影响

图7给出了不同数据量下单机环境和集群环境对算法性能的影响。数据维度为50，5名用户在最差情况下进行查询。从图7可以看出，随着数据集规模的增大，集群环境下的优势逐渐显现出来，集群环境下的系统并行性和处理能力均得到了增强，进而执行时间也越来越短。

Figure 7 Effect of different data volumes on algorithm performance图7 不同数据量对算法性能的影响

在单机和集群环境下，对相同数据量不同数据维度的数据集进行算法性能测试，结果如图8所示。数据量为5万条，5名用户在最差情况下进行查询。从图8中的实验数据可以看出，随着数据维度的不断提高，集群环境下的算法性能也逐渐与单机环境下的算法拉开差距，表明算法有良好的并行性。

Figure 8 Effect of dataset dimensionality on algorithm performance图8 数据集维度对算法性能的影响

在NBA球员真实数据集上分别进行单机环境和集群环境的算法性能测试的结果如图9所示。数据量默认为24 624条，5名用户在最差情况下分别以初始维度为28，34和40进行向下查询。

Figure 9 Performance test of the algorithm on NBA player dataset图9 NBA球员数据集上的算法性能测试

从图9可以看出，集群环境下的执行时间相较于单机环境均有降低，由于NBA球员数据集规模较小，导致在初始维度28时与单机环境下的差距不够明显，随着初始维度数量的增加，候选集中数据点的数量也逐渐增多，算法需要花费更多的时间进行处理，由于Apache Flink框架特性，MKSPSA算法在整个处理过程中避免了大量的时间消耗。因此，在处理大规模高维度数据集时，MKSPSA算法优于MKSSOA算法。

6 结束语

本文对多用户k-支配skyline查询问题进行了深入的研究。首先，提出了面向多用户的k-支配skyline体求解优化算法MKSSOA，该算法对每名用户的候选集和中间集分别进行存储，再根据两集合中数据点出现的先后次序对候选集进行k-支配检查，可以减少数据点之间的比较次数，从而更快地得到准确的结果集；随后，在此基础上提出了面向多用户的k-支配skyline体并行求解算法MKSPSA，该算法利用Apache Flink的并行性和算子特性，有效减少了数据点的比较时间，提高了算法效率；最后，通过理论研究和对比实验，验证了本文所提算法的有效性和高效性。未来的研究重点为针对k-支配skyline查询过程进行优化，以提高算法查询效率。