会展服务联盟收益分配研究*
——基于区间和模糊合作博弈视角
2023-02-08张佳玉孟凡胜杜泽文哈尔滨商业大学商务学院
文/张佳玉 孟凡胜 杜泽文(哈尔滨商业大学商务学院)
一、引言
随着市场经济的高速发展,会展业作为服务业的有利推手,当前正处于战略机遇期,我国正从会展大国走向会展强国,会展服务是会展“新业态”的重要环节,也是提升专业化水平的关键手段。2020 年我国会展界的联盟组织如雨后春笋般涌现出来,成立联盟、加入联盟逐渐成为一种常态,新冠疫情的冲击迫使会展企业抱团取暖,通过联盟的形式展开竞争,逐渐拉开了企业之间的差距。会展服务联盟模式是一种新的盈利模式,创新服务模式,淘汰一批服务方向不准确、服务内容质量水平低的会展企业,转而迎来的是效果更佳、品质更高的会展服务。
本研究旨在合作博弈状态下根据会展服务联盟成员的收益区间数,得出在时间、资源等各方因素的变化及不确定条件下的最优分配方案,合理地实现资源配置和利润分配。研究的意义在于解决会展服务联盟的关键问题,即利益分配问题,从区间模糊数的角度,在条件模糊情况下如何分配的策略,这为会展服务联盟成员的利益分配方案提供参考。分析盟友之间的博弈关系以及利益分配策略,有利于会展服务联盟平台的建设、会展服务供需结构的调整。
二、文献综述
会展服务作为一种无形产品,其在会展活动中构成了主导力量,在探究会展服务作为一种增值服务的过程中,作为会展服务的供需两方在会展活动的过程中通常会以合作的形式进行利益分配。会展服务的形式、价格以及收益分配等都影响着组展商、商协会、媒体三方之间的竞合关系,以联盟展开博弈进行利益的角逐。联盟的形式属于博弈中的合作博弈,博弈主体以自身利益为出发点,通过与其他博弈主体进行谈判协商寻求具有约束性合作的联盟,达成具有一定限制的合作契约。
Aubin(1974)将参与率介于 [0,1]这个区间概括为局中人参与联盟的程度[1],引出模糊联盟的概念,迎合了局中人的偏好和利益分配原则,对现实中的方案决策有着重要的应用价值。Shapley(1953)最早提出Shapley值的方法来解决利益分配问题[2]。Mare(2001)拓展了模糊联盟的概念[3],指出局中人在合作过程中更多地存在支付函数模糊的情况。于晓辉[4](2019)研究一种特殊的模糊支付合作对策,即具有区间支付的合作对策,并且给出了该区间Shapley 值形式。
国外学者在会展联盟方面的研究分析了联盟层面的治理及伙伴之间的协 调 问 题。Jarvenpaa & Välikangas[5](2016)认为会展项目方案存在无形性致使联盟的合作成果产权界定不明确,进而导致利益分配冲突的问题。Davis & Eisenhardt[6](2016)的研究表明联盟层面的合作高度依赖会展企业员工的知识和技能,隐性知识占比高,导致联盟资源难以共享与整合。国内学者白鸥[7](2020)以杭州会议产业联盟为案例对会展产业联盟的治理机制及其对联盟绩效的影响机理进行探索分析。通过文献的检索和梳理发现,学者注重会展产业联盟资源以及合理分配利益措施的探讨,鲜有利用合作博弈来探讨会展服务联盟成员的收益分配问题,关于模糊合作博弈结合其对会展服务联盟影响的研究较少。本文将会展服务联盟的盟友收益用区间模糊数表示,符合会展服务联盟参与者利润的弹性特点及会展项目运营的实际情况。
三、理论基础
(一)模糊合作博弈
何为合作博弈?指采用合作方式的过程中产生的合作剩余在博弈主体间的利益最大化的分配结果。由于客观世界的复杂性和人们主观能动性等原因,使得联盟中的企业参与联盟产生的合作剩余以及结果具有不确定性。所以企业之间的合作博弈具有模糊性,也可以称为模糊合作博弈,在具有模糊联盟结构的合作博弈中,联盟的参与水平对于联盟中的局中人来说是决策权行使与否的关键因素。
假设存在n个局中人,局中人集合用 Ν = {1 ,2, … ,n}表示, n =, n 为局中人个数,当n 确定时,可用模糊特征函数表示一个模糊联盟合作对策,二元组表示模糊联盟结构的合作对策。
定义1 模糊特征函数v˜是定义在Ν 的幂集 Q ( Ν )上取值在模糊数集合R上的模糊支付函数,,若Q ( Ν )→R ,满足:
(1)v (∅ ) =0 ;
(二)区间模糊的Shapley 值隶属函数
由于博弈信息的模糊性,因此必须研究联盟中企业的参与联盟水平为模糊变量时的建模方法和算法,而这类信息必须用到区间数来处理,Moore对区间数及其运算进行了基本的定义[9]。因为模糊支付合作对策和具有区间支付的合作对策有一定的对应关系,下面对相关概念进行界定。
基于区间Shapley 值,为了引出模糊Shapley 值需要引进集轮的概念。
定 义2 设Ψ 为 指 标 集, Χ 为论 域, Ρ ( Χ )为 Χ 的 幂 集, 对 于任 意是 从 区间到 Ρ ( Χ )的 一 个 映 射, 即且 映 射F 满 足 条件则 称F 为 上反同态映射。若上同态映射F 还满足F ( 0)= Χ,则称F 为集轮。
四、会展服务联盟收益分配模型
(一)会展服务联盟的界定和分类
当下会展服务联盟有多种形式,成员类型、目标、功能等都有所不同。本文将会展服务联盟界定为:立足于会展服务的市场需求,由提供会展服务的政府机构、商协会、媒体组织、组展商企业等组成,开展政策扶持、企业及产品的展示、宣传、推广、交易等活动,搭建服务平台为参展企业提供服务支持的组织。笔者对相关资料的整理如表1 所示。

表1 会展联盟类型
(二)会展服务联盟的收益分配方案
联盟的收益分配需要考虑到一个具体的n人合作联盟总收益,明确在合作结束之后如何进行联盟所得收益以合理且确定的形式分配给各盟友,根据所求的区间模糊Shapley 值隶属函数制定一套明确的收益分配方案。针对组展商、商协会、媒体三方在合作博弈中选择组成的会展服务联盟策略,考虑在会展项目运营存在人力、时间、资金、信息等资源的不确定性,将区间模糊Shapley 值引入到会展服务联盟成员收益分配方案中,会展服务联盟成员的收益在一个科学的浮动区间,运用模糊Shapley 值模型计算出会展服务联盟成员在不同联盟形式下的收益值。
根据上述相关内容,下面对基于区间模糊的Shapley 值分配方案进行介绍,具体的方案如下:
首 先,对 集 合中 的 元 素进 行 排 序, 即 若R≥, 则称≥。
最后,对n个局中人合作预期利益分配做出预测。对于任意给定的置信水平α∈,若联盟S的预期支付的区间数为,则此时局中人的分配区间数为:区间数表示局中人i的分配可能分布的区间范围,并且具有模糊支付的会展服务联盟利益分配问题转换为具有区间支付的利益分配问题;当 1α= 时,任意联盟S∈Q( Ν )的支付函数为一个确定的实数,则此时任意局中人i的分配也是一个实数。
(三)实例分析
在一个展会项目中,本身相互独立的组展商、商协会、媒体等进行资源的集中整合,追求展会的整体经济利益最大化,既有利于会展业在后疫情时代进行新旧动能的转化以及会展行业的良性发展,也提高了会展服务联盟中各盟友之间的利益所得。因此,展会活动可以看作是多人合作决策的过程,会展服务联盟中伙伴的收益分配可以看作是多人合作对策的收益分配问题。在模糊Shapley 值的模型当中,Ν 是n个企业的联盟体,S为Ν 中若干企业合作的联盟子集,S)为联盟S除去企业i的产生的收益。现假定有1、2、3 三个企业,分别代表组展商、商协会、媒体,三方合作一个展会项目,如若三方在展会项目实施的过程中不采取加入会展服务联盟的形式,则每个企业获利约为100 万元,如1、2 联合则可获利600 万元,如1、3 联合可获利550 万元,如2、3 联合可获利650 万元,如1、2、3 联合则可获利约1100 万元。上述支付函数均可用下面的模糊数形式表示:
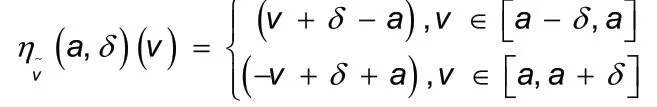
为了计算简便, 将上述三角 模 糊 数 统 一 记 为z(a,δ),所以支付函数可分别表示为:

({ 1 ,2,3} )(x) =z(1 100,200)。首先根据公式(1),计算模糊支付合作对策的Shapley 值的α截集,得局中人1 的Shapley 值。计 算 结 果 如2 所示,
通过表2,计算局中人1 的模糊支付Shapley 值截集的左端点和右端点分别为:

表2 局中人1的模糊Shapley值的截集计算表
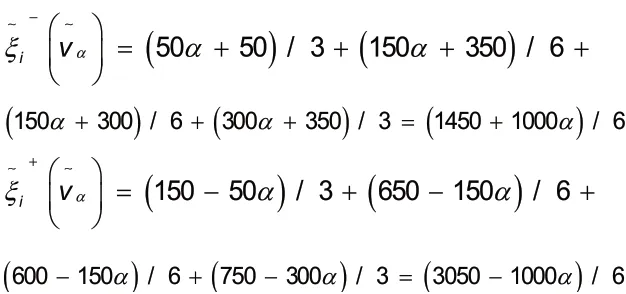
因此:
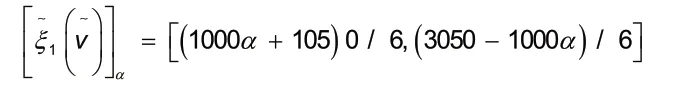
从结果可知其中心值分别为2050/6、2350/6 和2200/6,偏差度均为1000/6。表示局中人1、2、3 的收益分配值分别是2050/6 万元左右、2350/6万元左右和2200/6 万元左右。

同理可求得其他联盟组合下的Shapley 值以及不同联盟组合的会展企业收益分配策略。(如表3 所示):

表3 会展企业收益分配策略
表3 中的数据显示了三个局中人可供选择的所有的和合作策略的分配值,根据模糊数的排序方法“重心方法”计算出每个局中人的所有方案排序得到的最优策略。这个最优策略即三方共同合作参与的大联盟 S ={1 ,2,3}。最优策略显示形成三方的大联盟利润高于独立于大联盟之外的利润,并且高于{1 ,2} ,{1 ,3} ,{ 2,3} 两方形成的联盟利益。三个局中人参与合作联盟后可分别从中获利2050/6 万元左 右、2350/6 万 元 左 右 和2200/6 万元左右,模糊数为 z ( 2 050 / 6,1000 / 6)、z (2350 / 6,1000 / 6)、 z ( 2 200 / 6,1000 / 6)。
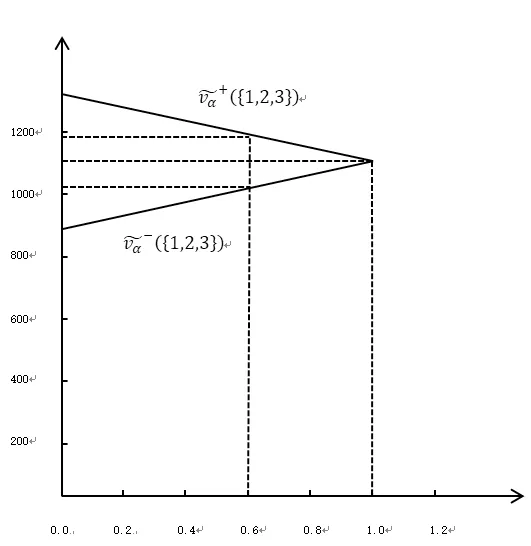
图1 局中人1,2,3合作总收益的截集
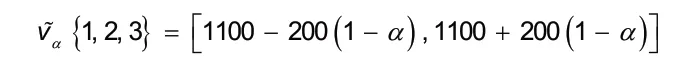
三个局中人的分配预测值区间分别为:

如图2 所示。
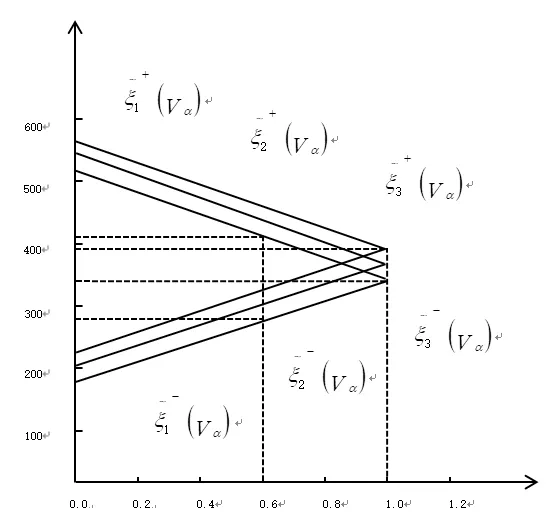
图2 局中人1,2,3在合作中所得分配的截集
若决策人置信水平 0α = ,则局中人1,2,3 的分配预测值为区间数和若决策人置信水平α = 0.5,则局中 人1,2,3 的分配预 测值为区间数;若决策人置信水平 α = 1,则局中人1,2,3 的分配预测值为精确值2050/6万元、2350/6 万元和2200/6 万元。
五、结论
运用模糊支付合作对策和区间模糊的Shapley 值,将支付函数用区间模糊数表示更加贴近现实,因为会展服务联盟的合作博弈存在不确定性,区间数可以更加贴近联盟伙伴因客观状况和主观策略浮动的收益水平。在组展商、商协会、媒体三方不采取进行合作博弈时,意味着不能形成联盟的结构。当形成联盟时又面临着与谁联盟、如何进行利益分配等情形,当联盟中只有局中人一个人时形成的联盟的获利仅为最小值;当联盟中有两个局中人时,获利相对于第一种情况获利增加;当联盟三者形成大联盟时获利达到最大。
