斜掠气梁充气翼湿模态分析与试验

孟繁敏，马诺，马文朝，孟军辉，2，*，李文光

1.北京理工大学 宇航学院，北京 100081

2.北京理工大学 飞行器动力学与控制教育部重点实验室，北京 100081

充气翼具有轻质、便携、低成本等优点，在小型无人机和巡飞弹等飞行器中有着较好的应用前景［1-3］，引发了国内外学者的广泛关注［4-7］。由于薄膜在气压作用下易产生大变形，现有充气翼设计通常采用多个内切圆方法逼近翼型，可分为多气梁式充气翼和多气管式充气翼［4］。基于气泡原理所提出的内切圆逼近翼型的方法，使得充气翼表面形成多个凹凸不平的波纹，进而导致其升阻特性降低［8-10］。同时柔性充气翼结构整体缺乏刚性连接，也使得其气动弹性问题较为突出［11-13］。复合材料翼面气动弹性裁剪可通过方向刚度设计，实现在载荷作用下产生最有利的变形。参考气动弹性剪裁的思想，通过将传统充气翼内切圆逼近翼型改为椭圆内切的形式，可实现充气翼的气梁沿翼展方向倾斜一定角度。依此所设计的充气翼，在相同气梁数目下翼面波纹的凹凸感减小，对目标翼型的逼近效果更为理想，同时通过设计气梁斜掠角θ理论上也可实现气动弹性性能的提升。为了验证斜掠气梁充气翼新构型设计改善气动弹性的有效性，通过数值仿真和地面振动试验（GVT）开展斜掠气梁充气翼结构动力学特性研究至关重要。

充气翼由高强度柔性复合膜材料封闭一定压力的气体制成，由于其轻质的特点，结构在空气中振动会带动周围部分空气一起振动，引起附加质量效应。分析充气翼自振特性必须考虑内外流场的耦合作用［14-16］，即对其进行湿模态分析。现有的湿模态分析方法主要包括虚质量法、流固耦合法和附加质量法3 类。虚质量法是一种通过施加一个附加质量矩阵，实现不可压缩流体对结构的作用，适用于包围结构或部分结构的无限流体，或者结构内部有自由表面的流体，如航行于海中且内部设置有水箱的船体［17］。此方法对于柔性充气结构适用性较差，在充气结构的湿模态分析领域较少使用。流固耦合法将流场视作声学单元，通过非对称求解器开展模态分析。高海健等［18］采用流固耦合方法对充气梁结构的湿模态开展研究；张祎贝等［19］分别采用流固耦合与声固耦合方法对简单膜结构在空气与低真空环境下的结构动力学特性进行分析，并对二者结果与试验进行对比分析。此方法由于需要考虑声压能量的扩散效应，往往需要构建足够大的流场单元以确保分析的准确性，因此导致了较高的分析成本。附加质量法是一种将流体作用视作附于结构表面质量点的湿模态分析方法，具有高效准确等优势。陈宇峰等［20-23］采用附加质量法分别对柔性飞艇与充气尾翼的湿模态进行分析。此方法虽然考虑了空气附加质量的影响，但忽视了流场对系统刚度的贡献。

为了研究斜掠气梁充气翼自振特性，本文在考虑空气附加质量影响的基础上，进一步计及流场对于系统刚度的贡献，提出了一种湿模态快速建模和仿真分析的方法，即附加质量-刚度法。通过经典柔性充气管算例验证了该方法的有效性，进而对传统直梁充气翼和斜掠充气翼湿模态进行了仿真分析。进一步搭建地面振动试验系统，在探究不同充气内压等参数对模态参数影响规律的基础上，对比分析直梁充气翼和斜掠气梁充气翼仿真分析和地面振动试验结果，以验证斜掠气梁构型设计对改善气动弹性的作用。

1 理论分析

1.1 薄膜振动理论

对于充气翼结构而言，薄膜完全依靠张力平衡面外载荷，张力主要由充气内压和大气外压之间的压力差提供。假设薄膜材料各向同性，对于厚度为h的张紧薄膜，其中微元的预应力膜平衡方程为［24］

式中：Tx、Ty分别为薄膜微元在x、y方向上的张力；p为压力。Tx、Ty分别可表示为

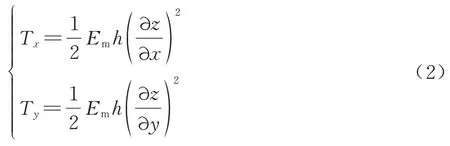
式中：Em为薄膜材料杨氏模量。将式（2）代入式（1），得到预应力膜结构的静力学平衡方程

预应力薄膜自由振动时，取薄膜充压变形后的形状作为参考构型。设xOy平面与薄膜静变形后的平面一致，与xOy平面垂直的z方向的振动位移w为小量，振动引起的张力变化可以忽略。在膜上取微元dxdy，薄膜面密度为ρ，dx与dy边上单位长度膜张力分别为Tx和Ty，如图1［24］所示。则薄膜自由振动的运动微分方程为

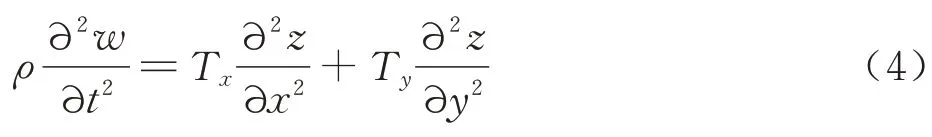
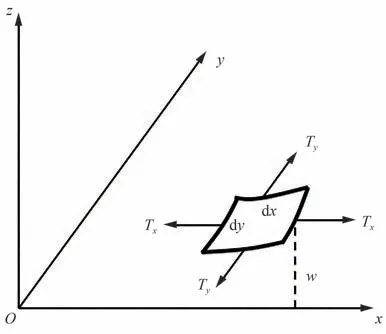
图1 薄膜振动示意图［24］Fig.1 Vibration of membrane［24］

1.2 湿模态建模方法

为研究带有气梁斜掠角的柔性充气翼结构振动特性，本文构建了一种考虑空气附加质量和流场刚度贡献的湿模态建模方法。该方法通过对流场的等效近似，将其视作与柔性充气结构固连的线弹性结构。空气附加质量Madded和流场对于系统刚度的贡献Kadded确定方法具体如下。

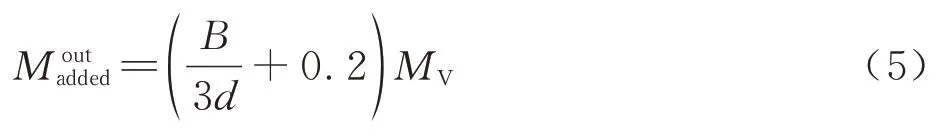
式中：B为结构宽度；d为结构浸润深度；MV为排开流体质量。

对于轻质充气结构而言，内部高压气体将伴随结构共同振动，其质量可表示为

式中：ρ(p)为流体密度对于压力的函数；Vs为结构内部充入气体体积。

因此，充气结构附加质量Madded可表示为

因此，基于经验公式所得的Madded将作为后续建模依据。

充气压力相比于大气压力量级较小时，体积弹性模量的变化可忽略不计，此时，建模过程中所需流场体积Vf为

式中：ρf为流体密度。

根据平均原则，流场可根据结构几何或边界条件确定，其形函数Nf可写作：

式中：Ns为充气结构形函数；n'为结构形函数法向矢量；Δx为流场内外边界距离。

流场形函数在内边界与结构形函数一致，表征流场内边界与结构共用节点；流场形函数外边界是由内边界单元法向上等距偏移获得；对于结构约束性边界，结构同流场均不参与振动，因此不予考虑。

对于均质流体，其微团具有与固体相似的控制方程形式［26］。而在伴随结构振动时，空气在可压缩性与黏性的作用下抵抗应力［27］。因此，根据各向同性材料弹性系数之间的关系［28］，在小扰动下流体的等效模量可表示为

式中：K为体积弹性模量；E为杨氏模量；υ为泊松比。

结合式（7）～式（10）即完成考虑空气附加质量和刚度贡献的流场等效模型构建。

则流场对于系统刚度的贡献Kadded为

式中：Ef为流场等效模量；I为流场惯量。

1.3 模态分析

对应一般n自由度结构系统，其运动微分方程有

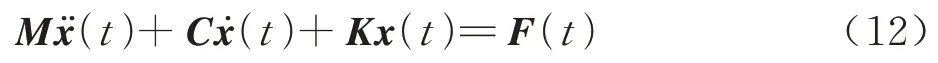
式中：M为n×n阶系统质量矩阵；C为n×n阶系统阻尼矩阵；K为n×n阶系统刚度矩阵；x(t)为L个点测量系统输出位移向量，则分别为速度和加速度向量；F(t)为P个点激励系统输入外载荷向量。模态分析对无外载荷和阻尼的模态矢量进行求解。假设系统外载荷和阻尼均为零，式（12）可简化为

对于充气结构湿模态研究而言，需要考虑内外流场附加质量的影响，即系统质量M包括充气膜结构自身质量Ms及周围振动的薄层空气质量Madded。其中Madded为前文所述基于经验公式所得的附加质量的矩阵形式。而现有研究中，通常并未考虑内外流场对于系统刚度的影响。实际上，系统刚度K同样包括平均分配的充气膜结构刚度Κs和流场对于系统刚度的贡献Kadded，即

式中：充气膜结构刚度Ks可具体表述为［21-22］

单元刚度矩阵Ke可写作

单元的线性刚度矩阵KL，e、初应力刚度矩阵Kσ，e和大位移刚度矩阵KNL，e可写作

式中：BL和BNL分别为单元线性部分应变矩阵和单元非线性部分应变矩阵；D为弹性矩阵；σ为应力矩阵；ds为面积微元。

自由振动微分方程式（13）的特解为

式中：φ为n维振幅；ω为固有频率；t为时间。将式（14）代入式（13）整理有

式（21）在系数矩阵行列式为0 时有非零解，即：

由式（22）可以解得n个根，通常将系统的固有频率ωi从小到大排列，称ω1为系统的第1 阶固有频率或基频。将任意特征值代入齐次方程（21）可得到与之相对应的特征向量φi，也称系统的第i阶固有模态或固有振型。

2 数值仿真

2.1 充气管验证算例

为验证本文构建的湿模态建模方法的准确性，首先采用一端固支的充气管作为验证算例，并与试验结果进行了对比。充气管算例所采用几何结构构型、材料及流场参数、边界条件设置均与文献保持一致［21］。本文构建的附加质量—刚度法建立充气管有限元模型如图2 所示，与各分析方法获取的充气管固有频率结论如表1 所示，对应模态振型如图3 所示。

图2 附加质量-刚度法建立的充气管有限元模型Fig.2 Finite element model of inflatable tube based on added mass-stiffness method

表1 充气管验证算例固有频率对比Table 1 Natural frequency comparison of inflatable tube

由表1 和图3 可知，干模态与试验结果相差较大，说明湿模态分析的必要性。由于无需采用非对称求解器，相较流固耦合法，本文构建的附加质量-刚度法在保证了较高精度的前提下，计算效率显著提升。而相比于传统的附加质量法［29］，本文对于周围流场振动时的等效刚度给予了充分考虑，改善了对于结构固有频率的预估效果。在该充气管验证算例中，本文构建的附加质量-刚度法对于前2 阶模态固有频率的相对误差分别为3.2%和0.8%，其计算精度满足后续柔性充气翼结构湿模态研究需求。

图3 充气管模态振型示意图Fig.3 Mode shapes of inflatable tube

2.2 斜掠气梁充气翼湿模态分析

基于附加质量-刚度法，本文对传统直梁式充气翼、前掠气梁充气翼和后掠气梁充气翼进行了湿模态分析。以NACA0015 为基准翼型，根弦长为450 mm，展弦比为2，根梢比为1，构建柔性充气翼结构有限元模型。3 种柔性充气翼结构的截面气梁数均为13，后缘半径为13 mm。如图4 所示，在机体坐标系Oxyz下，斜掠角θ定义为气梁方向与机翼展向的夹角，取后掠为正，则传统直梁式充气翼的斜掠角θ为0°，前掠气梁充气翼斜掠角θ取为-24°，后掠气梁充气翼斜掠角θ取为24°。充气翼表面气囊材料为高强度柔性层压薄膜材料，其主要力学参数如表2 所示。

表2 充气膜材料力学参数Table 2 Mechanical parameters of inflatable membrane

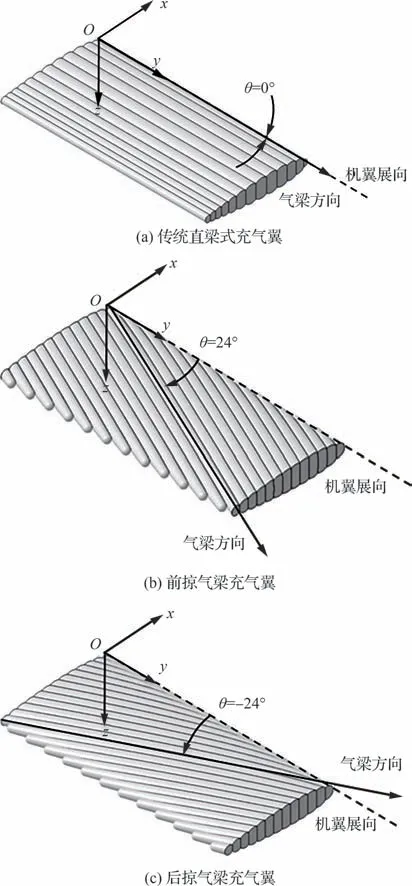
图4 柔性充气翼结构模型示意图Fig.4 Models of inflatable wings

其中，本文所研究的充气翼由柔性纤维编织复合材料制成，为正交各向异性材料，其经纬向力学性能差异较小，在工程估算中，可将其视作各向同性材料［30-32］。当充气内压足够维持薄膜局部刚度后，提高内压对结构整体刚度并无贡献，对固有频率影响较小［20-21］。基于上述参数设置，本文构建柔性充气翼结构模型如图4 所示。基于附加质量-刚度法，本文构建有限元模型如图5 所示。考虑内外流场影响的柔性充气翼结构湿模态分析，为简化建模过程，将充气翼结构内部压力气体折算至外流场，外流场实际体积由式（8）可得。外流场采用solid45 实体单元，充气翼结构采用shell181 壳单元，翼根为固支边界条件。区别于流固耦合法对于流场的描述，附加质量-刚度法仅考虑流场中参与结构振动的局部流场，有效节省了计算成本。相较于传统的附加质量法，附加质量-刚度法引入了对于流场等效刚度的考虑，实现了对结构振动特性更为准确的预估。

图5 基于附加质量-刚度法构建的充气翼有限元模型Fig.5 Finite element model of inflatable wings based on added mass-stiffness method

根据以上建模与分析方法，选取30 kPa 充气内压，该内压条件下薄膜结构已完全张紧，通过兰索斯法所进行模态分析可以获取反映结构整体模态的固有频率和模态振型。基于附加质量-刚度法的柔性充气翼结构湿模态分析结果见图6。由图6 可知，30 kPa 充气内压条件下，基于附加质量-刚度法的湿模态建模方法反映了传统直梁式充气翼的前5 阶模态，对照模态振型可知其分别反映了一弯、一扭、二弯、弦向一弯和二扭的振动模式，其中弦向一弯为柔性充气翼结构特有的振动模式，体现出区别于刚性机翼的显著特点。

图6 30 kPa 下传统直梁式充气翼仿真结果Fig.6 Simulation results of baffled type at 30 kPa

针对相同充气内压条件下，相同频率范围内的前掠气梁充气翼湿模态分析结果如图7 所示。由图7 可知，相同频率范围内前掠气梁充气翼仅有4 阶模态。相较传统直梁式充气翼，固有频率有一定变化，这是由于斜掠气梁充气翼中气梁方向的改变导致结构刚度轴产生偏移，反映到固有频率数值上有所变化。同时，由模态振型可知，前掠气梁充气翼的前4 阶模态分别反映了一弯、一扭、二弯和二扭的振动模式，相较于传统直梁式充气翼，显著消除了弦向模态，这是由于斜掠气梁充气翼的气室方向设计与机翼展向具有一定倾角（斜掠角θ），斜掠角θ的存在使得内部拉带既能提供展向支撑，也能提供机翼弦向支撑，斜掠充气翼结构弦向模态的消除对充气翼气动弹性的改善具有积极意义［24，33］。

图7 30 kPa 下前掠气梁充气翼仿真结果Fig.7 Simulation results of forward swept type at 30 kPa

同样的，基于附加质量-刚度法的后掠气梁充气翼仿真结果如图8 所示。由图8 可知，与前掠气梁充气翼相似，后掠气梁充气翼同样消除了弦向模态，尽管仍反映了一弯、一扭、二弯和二扭的振动模式，但由于斜掠角θ倾斜方向的改变，结构刚度轴偏转的方向有所不同，后掠气梁充气翼的固有频率和模态振型较前掠气梁充气翼有所区别。

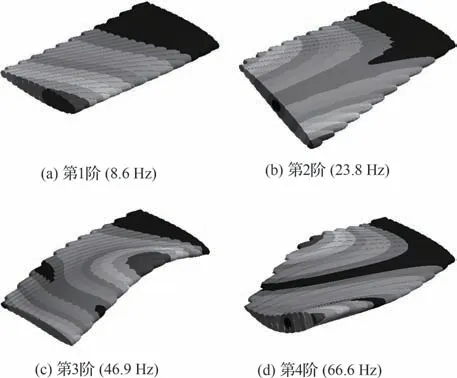
图8 30 kPa 下后掠气梁充气翼仿真结果Fig.8 Simulation results of swept type at 30 kPa

由于较轻的质量和较强的柔性，柔性充气翼结构的气动弹性问题通常较为突出，颤振失效是充气翼的典型失效形式之一，将直接危害飞行安全［34-35］。很多颤振分析实例表明，在颤振临界点附近，常有2 个分支在气流中的频率相互接近的现象，频率接近意味着2 个振型的耦合性加强，由此得到了一种高度简化的颤振理论，即频率重合理论［36-37］。参考文献［36］中定义为：当风速增大时，会使得2 个分支频率改变，一直到2 个频率重合。这2 个分支的耦合振动就有可能从气流中吸取能量，从而达到颤振临界点。因此，针对柔性充气翼结构，高效准确的构建有限元模型进行湿模态分析，获取包括固有频率在内的动力学参数作为气弹学科输入，将对后续颤振问题的分析具有直观贡献。

3 试 验

3.1 试验系统搭建

柔性充气翼结构地面振动试验测试系统包括柔性充气翼结构、力和加速度传感器、测量与分析系统和支撑台体4 部分，其设计方案流程图及实测图如图9 和图10 所示。

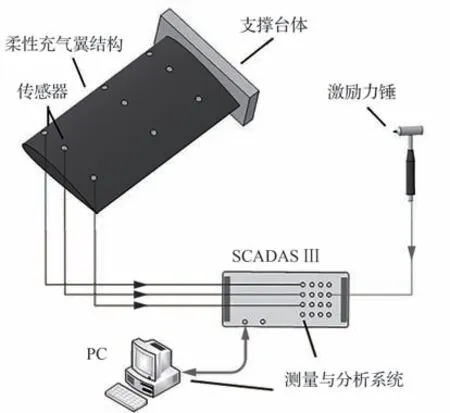
图9 柔性充气翼结构地面振动试验设计流程图Fig.9 Flowchart of GVT of inflatable wings

图10 柔性充气翼结构地面振动试验实测图Fig.10 Photo of GVT of inflatable wings

柔性充气翼结构测试样件由高强度复合柔性膜材料制成，目标翼面几何参数、充气翼结构几何参数和材料力学属性与数值仿真中模型保持一致。图10（a）为地面振动试验整体效果图，被测样件为传统直梁式充气翼，图10（b）为激励力锤，图10（c）和图10（d）分别为前掠气梁充气翼和后掠气梁充气翼测试现场图。充气翼支撑台体由金属型材搭建而成，为柔性充气翼结构提供一端固支、一端自由的边界条件。地面振动试验环境参数为(25±3)℃，相对湿度50%。

如图10（b）所示，本文选用PCB 086C03 冲击力锤，并针对柔性充气翼结构采用空气胶囊软锤头，以激发合适的脉冲信号，改善测试效果［38-40］。

力和加速度传感器分别用来测量结构所受到的激励信号和该激励作用下结构的动力学响应信号。如图10（a）所示，本文沿翼面均匀布置9个测量点，选用PCBTM 的333B30 加速度计获取响应信号。激励点选取柔性充气翼结构自由端近后缘测点进行激励，在传统直梁式充气翼和前掠气梁充气翼测试中，测点9 为激励点；在后掠气梁充气翼测试中，测点7 为激励点。

测量与分析系统选用LMS 的SCADASIII系统，可用于预设力和运动传感器的采样频率和采样时间，并对传感器采集到的激励信号和结构动力学响应信号进行处理。参照前文有限元仿真结果，至多关注柔性充气翼结构前5 阶模态参数，设置采样频率512 Hz，采样时间8 s，对于每个内压条件下的试件进行5 次敲击以消除测量误差，获取平均后的频响函数（Frequency Response Function，FRF），采用多参考最小二乘复频域法（Poly-reference LSCF，PolyMAX）进行辨识。

3.2 模态试验与结果分析

基于3.1 节所述试验系统，本文分别对传统直梁式充气翼、前掠气梁充气翼和后掠气梁充气翼3 个测试样件，在内压30 kPa、24 kPa、18 kPa、12 kPa 和6 kPa 共计5 个充气内压条件下进行了地面振动试验测试，获取5 次敲击下平均频响函数，通过PolyMAX 进行模态参数辨识，其固有频率测试结果随充气内压变化示意图如图11所示。

图11 反映了充气内压由6 kPa 递增至30 kPa的过程中，传统直梁式充气翼、前掠气梁充气翼和后续斜掠充气翼3 种测试样件固有频率均增大的趋势。在12 kPa 递增至30 kPa 的充气内压下，传统直梁式充气翼展现出了5 阶模态，前掠气梁充气翼和后掠气梁充气翼均展现出了4 阶模态。但当充气内压低至6 kPa 时，3 种测试样件均出现了模态缺失的现象，这一现象的出现将为本文柔性充气翼结构的最小控制内压提供参考。

图11 柔性充气翼结构地面振动试验固有频率测试结果Fig.11 Test results of inflatable wing natural frequencies

对于各充气内压条件下的柔性充气翼结构固有频率测试结果，分别计算了其第1 阶和第2阶的固有频率之比k，即

式中：ω1和ω2分别为柔性充气翼结构第1 阶和第2 阶模态的固有频率。对于传统直梁式充气翼、前掠气梁充气翼和后掠气梁充气翼3 种样件，各充气内压条件下k计算结果如图12 所示。

图12 柔性充气翼结构第1 阶和第2 阶固有频率之比Fig.12 Natural frequency ratio of Mode1 and Mode 2

由图12 可知，包括前掠气梁充气翼和后掠气梁充气翼在内的2 种斜掠气梁充气翼，其第1 阶和第2 阶模态固有频率之比k均低于传统直梁式充气翼，根据颤振分析频率重合理论［36-37］，更低的固频之比k对于提升柔性充气翼结构颤振速度、改善气弹特性具有积极意义。

3.2.1 传统直梁式充气翼

由图11 可知，在充气内压为12～30 kPa 时，传统直梁式充气翼固有频率变化趋于稳定，尤其第1 阶和第2 阶固有频率仅随内压上升有微弱增加。30 kPa 内压条件下，前5 阶试验测试结果如图13 所示。其中，虚线为参考几何构型，实线部分表征了试验测得的归一化模态振型。

图13 30 kPa 下传统直梁式充气翼试验结果Fig.13 Test results of baffled type at 30 kPa

如图13 所示，传统直梁式充气翼前5 阶模态测试结果分别反映了第1 阶一弯、第2 阶一扭、第3 阶二弯、第4 阶弦向一弯和第5 阶二扭的振动模式。上文结果以30 kPa 为例进行说明，实际上在充气内压由12 kPa 递增至30 kPa 的过程中，该5阶模态均能得到完整体现，除固有频率随充气内压增大略有上升外，模态振型所反映的振动模式完全一致，因此不再一一赘述。同时，试验测试结果与数值仿真结果具有一致性，从而进一步验证了附加质量—刚度法的准确性。

充气内压低至6 kPa 时，相同频率范围内充气翼测试结果出现了模态缺失的现象，传统直梁式充气翼测试结果仅剩余3 阶模态，如图14 所示。由图14 可知，在6 kPa 的充气内压条件下，传统直梁式充气翼仅剩3 阶模态，其中第1 阶模态振型已经出现了激励点振幅较大的情况，但前2阶模态振型仍总体反映了一弯和一扭的振动模式。与12～30 kPa 内压条件下测试结果显著不同的是，6 kPa 下的第3 阶模态振型同时呈现出了二弯和弦向一弯相互耦合的振动模式。考虑原因为在较低的充气内压条件下，较低的膜面刚度致使测试过程中难以激发结构整体模态，结构非线性十分显著，基于线性系统假设的模态测试结果已不能完全反映该充气内压下的柔性充气翼动力学特性。

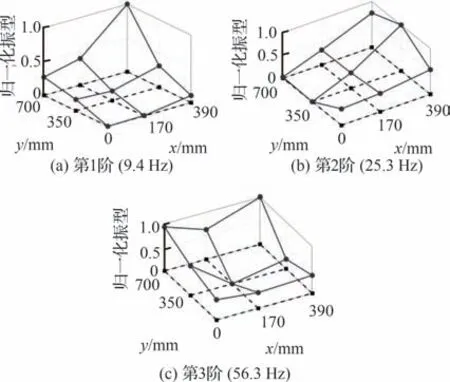
图14 6 kPa 下传统直梁式充气翼试验结果Fig.14 Test results of baffled type at 6 kPa

因12～30 kPa 充气内压下的充气翼测试结果具有高度一致性，均能完整反映前5 阶模态（第1 阶一弯、第2 阶一扭、第3 阶二弯、第4 阶弦向一弯和第5 阶二扭），以30 kPa 充气内压测试结果为例，图15 给出了30 kPa 和6 kPa 充气内压条件下测试获取的传统直梁式充气翼结构集总函数（所有测点的频响函数之和）。

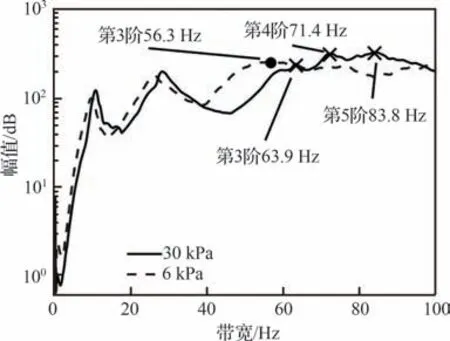
图15 30 kPa 和6 kPa 下传统直梁式充气翼集总函数Fig.15 Sum FRF of baffled type at 30 kPa and 6 kPa

对比30 kPa 充气内压条件下第3 阶63.9 Hz、第4 阶71.4 Hz 和 第5 阶83.8 Hz 共3 阶模态，6 kPa 充气内压条件下该3 阶模态振动模式趋向耦合，退化为一个趋势并不显著的峰值，即6 kPa集总函数中的第3 阶56.3 Hz 模态。该现象解释了图14（c）中具有耦合效应的模态振型，为本文传统直梁式充气翼许用内压的选取提供了参考。

为保证充气翼承载能力和气动外形，并在地面振动试验中具有足够大的系统刚度便于激发结构整体模态，为数值仿真提供参考，需要在综合考虑膜材强度、刚度等材料特性的基础上合理选取柔性充气翼结构最小控制内压，确保薄膜在许用应力的范围内有效张紧。如图15 所示，针对地面振动试验中确定膜材参数的传统直梁式充气翼，在充气内压12 kPa 及以上时，前5 阶测试结果均为整体模态，固有频率变化趋于稳定，振动模式趋势显著，完整反映了第1 阶一弯、第2 阶一扭、第3 阶二弯、第4 阶弦向一弯和第5 阶二扭的振动模式，证明该充气内压条件下的充气膜结构张紧，充气内压足够维持薄膜局部刚度，锤击激励得以激发结构整体模态，动力学测试结果具有参考意义。在综合考虑充气膜刚度和强度的基础上，选取12 kPa 可作为本文传统直梁式充气翼结构的最小控制内压。

3.2.2 前掠气梁充气翼

参照传统直梁式充气翼测试流程，本文对前掠气梁充气翼测试样件进行了地面振动试验。由图11 可知，前掠气梁充气翼固有频率随充气内压变化趋势与传统直梁式充气翼保持一致。但有别于传统直梁式充气翼，前掠气梁充气翼仅剩余4 阶模态。30 kPa 内压条件下，前4 阶试验测试结果如图16 所示。

图16 30 kPa 下前掠气梁充气翼试验结果Fig.16 Test results of forward swept type at 30 kPa

对比分析模态振型可知，前掠气梁充气翼剩余4 阶模态，分别反映了第1 阶一弯、第2 阶一扭、第3 阶二弯和第4 阶二扭的振动模式，显著消除了传统直梁式充气翼的弦向振动模态，这一现象与数值仿真结果相吻合，也侧面验证了附加质量-刚度法的准确性。

充气内压低至6 kPa 时，较低的膜刚度同样导致了模态缺失的现象，如图17 所示。由图17可知，与传统直梁式充气翼相似，充气内压低至6 kPa 时，尽管第1 阶和第2 阶模态振型较为清晰，但已经显现了激励点振幅过大，振型相位不一致的问题，第3 阶的模态振型更是出现了二弯和二扭相互耦合的振动模式。同样地，图18 给出了前掠气梁充气翼结构集总函数。

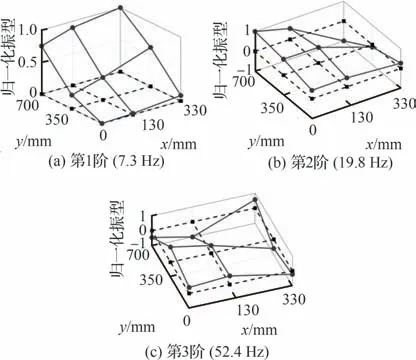
图17 6 kPa 下前掠气梁充气翼试验结果Fig.17 Test results of forward swept type at 6 kPa

图18 30 kPa 和6 kPa 下前掠气梁充气翼集总函数Fig.18 Sum FRF of forward swept type at 30 kPa and 6 kPa

与传统直梁式充气翼相似，30 kPa 内压条件下，第3 阶51.0 Hz 和第4 阶73.0 Hz 模态随充气内压的下降，退化耦合为一个同时包含二弯和二扭2 种振动模式的模态峰值，即6 kPa 内压条件下的第3 阶52.4 Hz 模态。在该内压条件下，较低的充气膜刚度致使试验过程中难以激发结构整体模态，结构非线性较为显著，测试结果难以具有参考价值，同样可选取12 kPa 为前掠斜掠气梁充气翼的最小控制内压。

3.2.3 后掠气梁充气翼

由图11 可知，后掠气梁充气翼测试结果与前掠气梁充气翼具有较高的相似性，30 kPa 内压条件下前4 阶测试结果如图19 所示。由图19 可知，后掠气梁充气翼前4 阶模态分别反映了第1 阶一弯、第2 阶一扭、第3 阶二弯和第4 阶二扭的振动模式，并同样消除了弦向模态，测量结果与数值仿真具有较高的一致性，进一步验证了附加质量-刚度法的准确性。

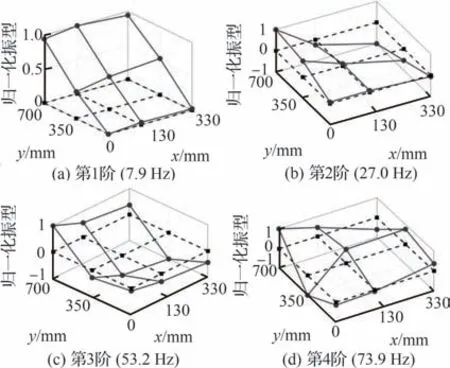
图19 30 kPa 下后掠气梁充气翼试验结果Fig.19 Test results of swept type at 30 kPa

6 kPa 内压条件下，后掠气梁充气翼同样出现了模态缺失的现象，剩余3 阶模态测试结果如图20 所示。

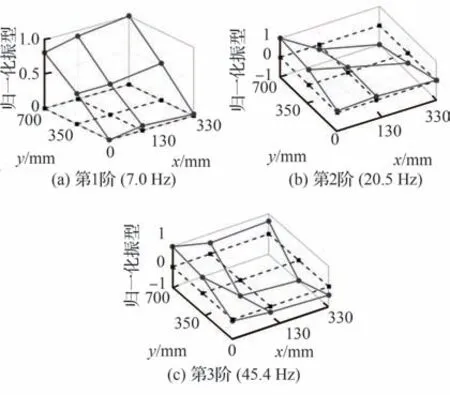
图20 6 kPa 下后掠气梁充气翼试验结果Fig.20 Test results of swept type at 6 kPa

如图21 所示，与前掠气梁充气翼相似，集总函数解释了模态振型相互耦合的趋势。为确保测试结果具备参考性，选取12 kPa 为后掠斜掠气梁充气翼的最小控制内压。

图21 30 kPa 和6 kPa 下后掠气梁充气翼集总函数Fig.21 Sum FRF of swept type at 30 kPa and 6 kPa

3.3 仿真与试验对比分析

本文基于附加质量-刚度法进行了湿模态仿真分析，并通过地面振动试验加以验证，针对传统直梁式充气翼、前掠气梁充气翼与后掠气梁充气翼的仿真与试验结果对比如表3 所示。

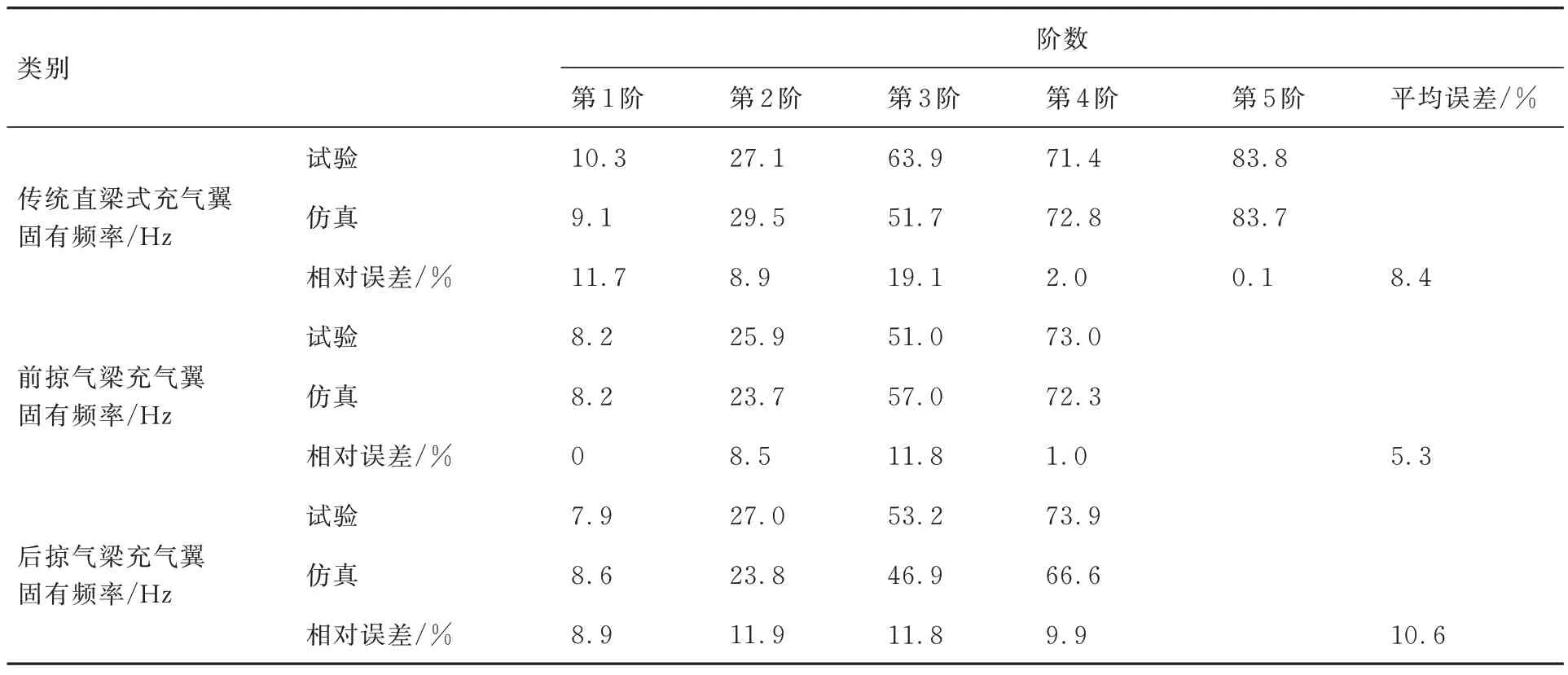
表3 固有频率仿真与试验结果对比Table 3 Natural frequency comparison between simulation and test results

表3 中，试验与仿真结果对应充气翼充气内压为30 kPa。由相对误差可知，基于附加质量-刚度法进行的湿模态分析结果与地面振动试验测试结果具有一致性。其中，传统直梁式充气翼、前掠气梁充气翼和后掠气梁充气翼分别取得了8.4%、5.3%和10.6%的平均相对误差，对于传统直梁式充气翼和前掠气梁充气翼的固有频率，本文构建的湿模态建模方法计算精度较高，平均相对误差保持在10%以下。对于后掠气梁充气翼，在试验测试中，由于样件加工的局限性，致使充气翼自由端外连接了充气管及气压表等相关配件，尽管实测过程中，通过弹性绳悬吊等方式尽可能降低了自由端附加质量的影响，但测试过程中系统质量的增大仍导致了高阶固有频率的总体降低，导致一定的相对误差。

4 结论

在考虑空气附加质量影响和流场对于系统刚度贡献的前提下，提出了一种湿模态快速建模方法，即附加质量-刚度法，对包括斜掠气梁充气翼在内的柔性充气翼结构进行了湿模态分析，并通过地面振动试验加以验证，结果表明：

1）本文所构建的附加质量-刚度法，相较于流固耦合法降低了分析成本，相较于传统附加质量法考虑了流场对于系统刚度的贡献，针对前掠气梁充气翼，湿模态数值仿真结果与地面振动试验平均相对误差为5.3%，能够实现湿模态快速准确估计。

2）地面振动试验中，柔性充气翼结构固有频率随充气内压上升而增加。充气内压低至6 kPa 时，较低的膜面刚度会导致测试过程中难以激发系统整体模态，结构非线性问题较为显著，基于线性系统假设的模态测试结果难以完全反映该充气内压下的柔性充气翼动力学特性。为确保激发结构整体模态，本文选取12 kPa 为测试样件的最小控制内压。

3）针对斜掠气梁充气翼结构，本文基于附加质量-刚度法和地面振动试验开展了动力学特性研究。由数值仿真和地面振动试验结果表明，相较于传统直梁式充气翼，斜掠气梁充气翼的第1 阶和第2 阶模态具有更低的固有频率之比，且能够显著消除弦向模态，对柔性充气翼结构提高颤振速度、改善气弹特性具有积极意义。