基于RBF 和主动学习的非概率可靠度求解方法

姜峰，李华聪，符江锋，洪林雄

西北工业大学 动力与能源学院，西安 710072

在实际工程问题中存在着大量不可避免的不确定性因素例如：制造误差、材料特性、载荷等等。作为结构设计和安全性分析中最重要的环节，结构可靠性分析必须对这些不确定因素进行合理的处理。长期以来，基于概率论的概率可靠性模型和基于模糊理论的模糊可靠性模型是工程中处理结构可靠性最普遍的模型，这2 种模型均从概率的角度来度量系统的可靠程度［1］。然而这2 种模型对数据信息的要求较高，当结构样本较少时，2 种方法无法从概率的角度对可靠性进行较好的描述。相对于精确的统计数据，在工程中不确定变量的不确定边界是容易确定的，针对这一特点，20 世纪90 年代，Ben-Haim 和Elishakoff［2］首次提出了非概率可靠性模型，通过国内外大量学者的研究该模型得到了很好的完善与发展。

不同于概率可靠性模型，在非概率可靠性模型分析过程中不确定变量釆用非概率的凸模型来描述。这里的凸模型代表一系列模型而不是单个模型，其中包括区间模型［2］、超椭球模型［3］、多维平行六面体模型［4］、超参数凸模型［5］、多模态椭球模型［6］等。目前应用较为广泛的凸模型是区间模型和超椭球模型［7-9］，已有学者基于这2 种模型针对实际的工程问题开展非概率可靠性分析工作：张屹尚等［10］基于超椭球模型建立了流固耦合管道系统的非概率可靠性综合分析方法；辛腾达等［11］基于区间模型对液体推进剂贮箱的非概率可靠性进行评估。相较于区间模型，超椭球模型具有姿态灵活与边界圆润的优点，在一般情况下它能提供更加紧凑的不确定域，更重要的是超椭球模型可以描述不确定变量之间的相关性［12］。因此，基于超椭球模型的非概率可靠性分析在实际工程应用中显得更为重要。

非概率可靠性模型背景下，如何对非概率可靠性进行度量是非概率可靠性理论的关键问题。针对这一问题大量学者进行了研究，洪东跑等［13］研究不确定性参数容差与偏差的关系，提出了基于容差分析的非概率可靠性度量方法。孙海龙和姚卫星［14］基于区间应力-强度干涉模型，提出了非概率可靠性分析的可能度法。不少学者利用标准参数空间中按不同形式的范数度量从坐标原点到极限状态面的最短距离定义了非概率可靠度指标用于衡量非概率可靠性，例如郭书祥等［15］基于区间模型，提出非概率可靠度指标为在标准化区间变量的扩展空间中，按无穷范数度量的从坐标原点到极限状态面的最短距离。Cao 和Duan［16］基于单一超椭球模型，定义非概率可靠度指标为标准化单位椭球扩展空间中，从坐标原点到极限状态曲面的最短距离。罗阳军等［17］基于多椭球模型，以原点到极限状态曲面的广义最小无穷范数来度量结构的非概率可靠性。Meng等［5］提出了超参数凸模型，并以原点到极限状态曲面的最小p 范数定义非概率可靠度指标。无论基于哪种形式的范数，从本质上看，非概率可靠度指标的定义只包含了极限状态曲面上最可能失效点这一点的信息，这对于不发生干涉时衡量结构的绝对安全程度是合理的，同时也具有明确的物理意义，但当失效域与不确定域发生干涉时，结构的绝对安全已不存在，只考虑最可能失效点这一点的信息是相对不够的，应该考虑干涉域的信息并对其进行度量才合理［18］，因此提出了基于体积比的非概率可靠度概念。王晓军等［19］针对区间应力-强度干涉模型，以体积比度量结构的非概率可靠性。乔心州等［20］基于上述思想，构建了基于超椭球模型的非概率可靠性模型，仍以安全域体积与不确定域体积之比作为非概率可靠性的度量。Meng 等［21］将非概率可靠度的概念扩展至超参数凸模型中，并开展了优化工作。非概率可靠度指标和非概率可靠度可以适用不同的凸模型，具有很好的应用前景。针对非概率可靠性度量方法寻找高效的求解策略也是非概率可靠性研究的一个关键问题，不同的非概率可靠性度量方法求解策略也不同，本文将主要基于非概率可靠度的求解展开工作。

由于非概率可靠度是基于体积比进行计算的，因此Meng［21］和Jiang［22］等提出了非概率可靠度的MCS（Monte Carlo Simulation）求解方法。但是MCS 方法计算量巨大在实际工程中难以应用，为了提高非概率可靠度的求解效率，Jiang 等［22］提出了一阶近似（FOAM）和二阶近似（SOAM）方法，其中二阶近似方法在处理强非线性问题时具有更高的精度。然而，上述方法存在很大的局限性，首先一阶和二阶近似方法都是在最可能失效点进行近似，寻找最可能失效点很容易出现不收敛的现象；其次即使是SOAM 方法也无法对某些复杂系统（例如串并联系统）进行较好地近似。在对大型复杂结构隐式功能函数问题进行概率可靠性分析时，一般会采取代理模型结合主动学习的方法，这种方法不仅有着较高的求解精度，同时有着较高的效率［23-25］。因此，张屹尚［26］基于ERF（Expected Risk Function）学习函数利用主动学习方法对非概率可靠度进行求解，取得了不错的效果。但是主动学习方法十分依赖Kriging 模型能够直接评估模型预测不确定性的特性，这一方面使得主动学习的方法难以与其他代理模型相结合，另一面由于Kriging 模型结构的随机过程部分，即使忽略初始样本的不确定性，Kriging 模型仍会产生随机结果，影响了主动学习结果的稳定性。

众所周知，不同的代理模型各有特点，对于不同复杂程度的工程问题具有不同的适用性。最近，主动学习结合其他代理模型的方法已被提出用于结构概率可靠性分析［26-29］。由于RBF 模型结构简单、参数较少且具有各向同性，可以更好地平衡计算效率和拟合精度［30］，因此本研究采用交叉验证的方法，基于RBF（Radial Basis Function）插值模型和主动学习方法，针对工程中广泛应用的超椭球模型进行非概率可靠度的求解。本文首先结合交叉验证和jackknifing 方法评估RBF 模型的预测不确定性，并采用一种高效的学习函数来指导主动学习过程。最后，提出一种适用于该主动学习方法的收敛准则，以提高算法的效率。

本文的主要框架组织如下：第1 节中回顾了超椭球模型的相关概念以及超椭球模型下非概率可靠度的定义，同时给出了非概率可靠度的MCS 求解方法。第2 节基于RBF 模型，给出了本文采用的具有相应收敛准则的主动学习方法。第3 节中给出了3 个数值算例来验证算法的有效性。最后，在第4 节中对全文进行总结。

1 超椭球模型下非概率可靠度定义方法

1.1 单失效模式下非概率可靠度定义方法

超椭球模型具有概念清晰、参数变化范围连续可微、模型简单并能反映变量之间的相关性等优点，因而受到了广泛的关注［31］。在超椭球模型中，不确定参数的变化范围为一高维椭球体。

对于n维变量x=[x1，x2，...xn]T，超椭球模型可以采用如下的公式进行表示：

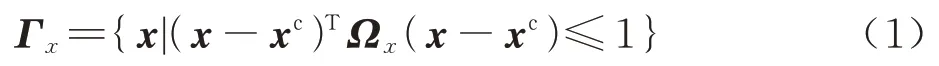
式中：xc为超椭球模型的中心点；Ωx为椭球的特征矩阵且为半正定矩阵，通过Ωx可以确定超椭球域的大小以及超椭球主轴的走向。如图1 所示对于单个变量xi，其可能的取值范围将构成一个区间为边缘区间的下边界为边缘区间的上边界，该区间称为边缘区间［6］。

图1 二维超椭球模型Fig.1 A two-dimensional hyper-ellipsoidal model

设结构的功能函数为

考虑如图1 所示的二维问题，二维问题中超椭球将退化为一个椭圆。整个椭圆域被极限状态面（即Y(x)=0）分割成2 个区域：安全区域（即可靠域）（Y(x)≥0）和失效区域（Y(x)＜0）。因此二维问题中，非概率可靠度Rc可以定量的表示为［20］

式中：A表示整个椭圆域的面积；A1表示结构的失效域面积；A-A1表示结构的安全域面积。类似地，如图2 所示，对于三维问题而言，上述的定义方法也具有同样的适用性，此时，面积比将被拓展为体积比。显然，式（3）的定义可以很容易地应用到一个n维问题中，在n维问题中非概率可靠度定义为2 个多维体积的比值，因此，式（3）可以作为非概率可靠度的一般定义。相应地，就像失效概率在传统的可靠性分析中定义的一样，超椭球模型下结构的危险度fc可以定义如下：

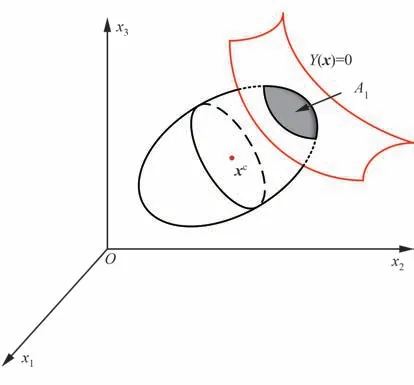
图2 三维超椭球模型Fig.2 A three-dimensional hyper-ellipsoidal model

1.2 系统非概率可靠度定义方法

非概率可靠度Rc不仅可以度量单失效模式下结构的非概率可靠性，同时也可以对系统的非概率可靠性进行度量。首先将考虑串联系统的非概率可靠度Rsceries。对于一个串联系统其极限状态方程可以表示为

如图3（a）所示，从几何上看，极限状态面是一个连续但不光滑的表面。阴影区域代表超椭球模型中落入失效域的部分，其多维体积表示为As1。因此对于串联系统，根据式（3），串联系统的非概率可靠度可以表示为

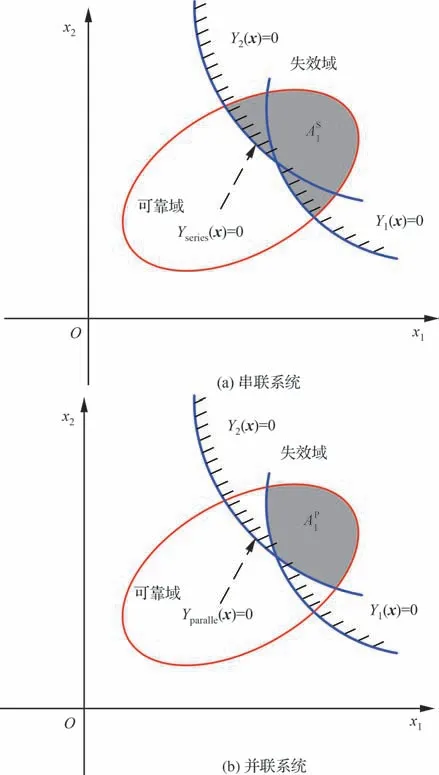
图3 串并联系统非概率可靠度Rc 定义方法Fig.3 System reliability analysis using nonprobabilistic reliability Rc

对于一个并联系统而言，其极限状态方程可以表示为

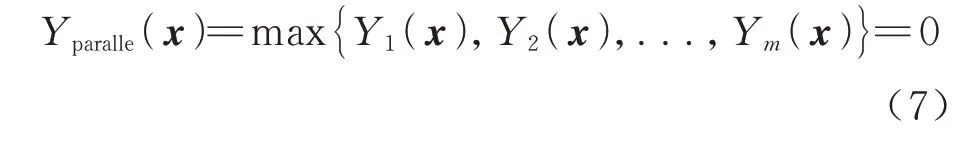
从几何上看，并联系统的极限状态面也是一个连续但不光滑的表面。如图3（b）所示表示超椭球模型落入失效域中的多维体积，因此根据式（3）并联系统的非概率可靠度可以表示为

1.3 非概率可靠度求解的MCS 方法

在概率论中，MCS 是一种极其重要的可靠性分析抽样方法，它可以提供足够精度的计算结果。因此，参考文献［21］，非概率可靠度求解的MCS 方法如下：

式中：Γx为超椭球不确定域；Γsafe=Γx∩{x|Y(x)＞0 }为安全域分别代表第i个不确定变量边缘区间的上界和下界；项是样本的联合概率密度函数，可以看出MCS 方法抽取的样本服从由各个变量的边缘区间构成的超立方体中的均匀分布；E[·]表示期望函数；I(·)为示性函数；可以表示为

随后，基于式（9）的采样方法改写如下：

式中：m是总样本数是近似非概率可靠度，它通过抽样方法计算得来的。从式（9）可以看出，是Rc的无偏估计。

式中：Va（r·）表示方差；

综上所述，本文的抽样方法通过以下4 个步骤计算非概率可靠度：①根据联合概率分布函数在由各个变量的边缘区间构成的超立方体中生成足够多的样本；②通过式（10）和式（11）计算每个样本的示性函数；③根据式（12）计算结构的非概率可靠度；④计算，应保证计算得到的小于5%［21］，如果不满足条件，返回步骤①扩充样本池。

2 基于RBF 和主动学习的非概率可靠度求解算法

当不确定参数用超椭球模型来描述时，参数在超椭球域内取任意一点的可能性是相同的，从概率角度而言，可以看作参数在超椭球域内服从均匀分布［8，12］。因此，可以将超椭球域内均匀分布的样本点作为候选样本点，采用基于代理模型的主动学习方法求解非概率可靠度。

2.1 RBF 模型

RBF 模型由对称径向函数线性组合而成，具有出色的计算效率和拟合精度。该方法本质上就是：对于假设的n维函数f=Y(x)，在已知k个样本点X={x1，x2，…，xk} 及其响应值Y=的情况下，用径向基函数来近似表示函数Y(x)。具体函数形式如下：

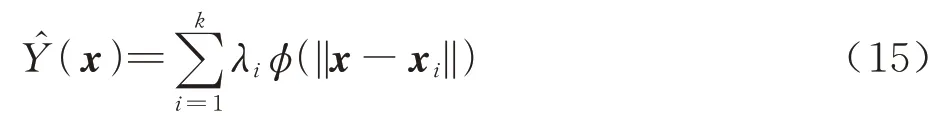
式中：x表示预测点；xi表示第i个已知样本点；λi表示第i个基函数的权重系数；ϕ表示基函数。

式（15）可以转换为如下的矩阵形式：

式中：λ=[λ1，λ2，...λk]T为权重系数矩阵；Φ是与预测点以及k个已知样本点相关的1×k维函数矩阵表示为

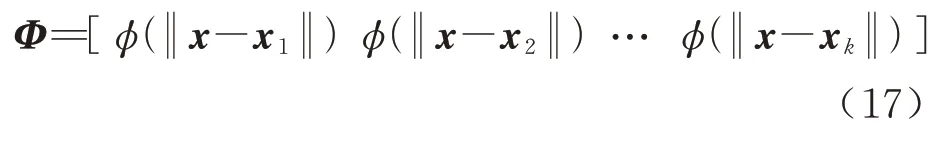
RBF 模型常用的基函数有多二次型、逆多二次型、高斯型等，本文采用多二次型基函数，具体形式如下：

式中：c表示径向基函数形状参数，c≥0，本文采用k折交叉验证的方法确定该参数；r=||x-xi||表示预测点与已知样本点之间的欧式距离。

为了确定权重系数矩阵λ，引入插值条件：

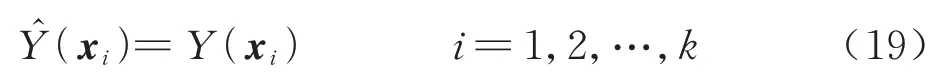
结合合式（15），式（19）可以转换为如下矩阵形式：

式中：Ai，j=ϕ(‖xi-xj‖)。通过求解方程组可求得权重系数矩阵λ，即：

2.2 RBF 模型的方差预测

众所周知，Kriging 模型可以根据预测方差评估样本预测响应的不确定性。如果一个样本点的预测响应不确定性较大意味着该点的预测响应精度较低，将该点加入训练样本集可以对代理模型进行更好的改善。然而RBF 模型并不具备直接评估预测响应不确定性的能力，因此本文基于k折交叉验证结合jackknifing 估计方法推导出jackknifing 方差［32］，以此度量RBF 模型下样本点预测响应不确定性的大小，具体方法如下：

将初始样本点以及响应S={(x1，Y(x1))，(x2，Y(x2))，…，(xk，Y(xk))}随机分 为ks个子集，其中是Scv中的第l个子集。

依次移除第l个子集，将剩余的ks-1 个子集作为训练样本，最终，得到ks个训练样本集合：

根据ks个训练样本集和完整的样本集Scv构建ks+1 个RBF 模型：

基于MCS 方法，生成候选样本集Sc={x1，x2，…，xN}。同时，计算ks+1 个RBF 模型在候选样本点处的预测响应。

由于训练样本的差异性，建立的各代理模型得到的候选样本点的预测响应也是不相同的。预测响应之间的差异越大，表明样本点处预测响应的不确定性越大，预测响应的精度越低。因此可以采用这些响应值之间的差异来表征代理模型在各候选样本点处预测响应不确定性的大小。下面根据jackknifing 方法对预测响应的不确定性进行量化［32］。

根据jackknifing 方法，候选样本点xi处的pseudo 值定义为

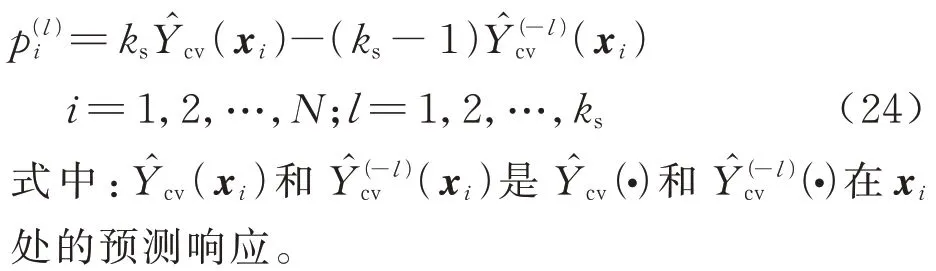
根据pseudo 值，候选样本点xi处的jackknife方差表示为

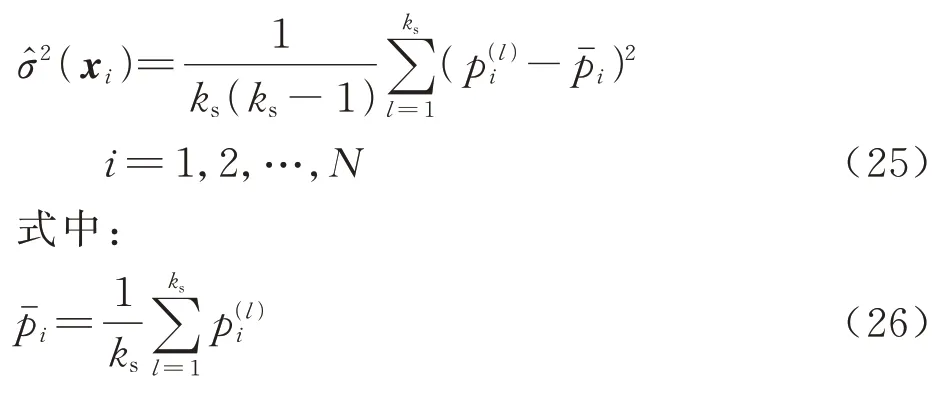
式（25）是不确定性量化的结果，这是主动学习函数的重要组成部分越大的样本点预测响应不确定性越大，精度越低，在主动学习的过程中被选中的可能性应该更高。此外，参数ks对方差估计的效率有很大影响。如果ks等于初始样本集的大小，则交叉验证方法可以充分考虑所有样本，可以大大提高估计精度。然而，随着初始样本量的增加，估计速率将显著放缓。考虑到效率和精度，本文将ks取为10。

2.3 主动学习方法

在主动学习的过程中，主动学习函数扮演着重要的角色。研究采用了一种已被成功应用于概率可靠性分析的Hrb学习函数［29］进行样本点的选取工作。

2.3.1 基于RBF 模型的Hrb主动学习函数

通过初始样本集S{(x1，Y(x1))，(x2，Y(x2))，…，(xk，Y(xk))}构建RBF 模型，为了进一步提高代理模型的拟合精度，需要从候选样本Sc={x1，x2，…，xN}中选择最佳样本点用于模型的迭代更新。

对于结构可靠性问题，主要考虑极限状态面附近的拟合精度。因此，在原有RBF 模型的基础上，将部分按照直线进行翻转，即在改善期望值的计算过程中，点x处的预测响应变为

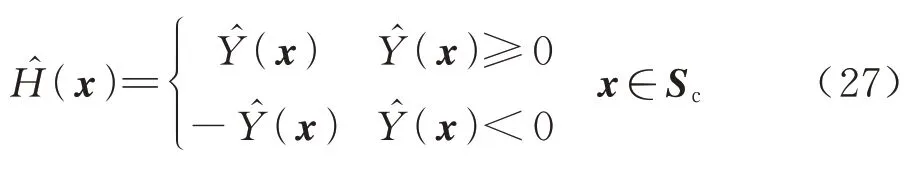
对于当前RBF 模型，集合Sc中最小响应被重新定义为

由于最佳候选点一般分布在极限状态面（LSS）的两侧，因此当候选样本点的数量足够大时，最小响应Hmin接近于0。因此在后续的推导中最小响应Hmin直接设为0。任意点x对代理模型的改善程度表示为

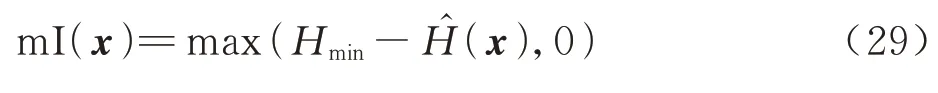
式中：m（Ix）也是一个随机变量，其期望值为

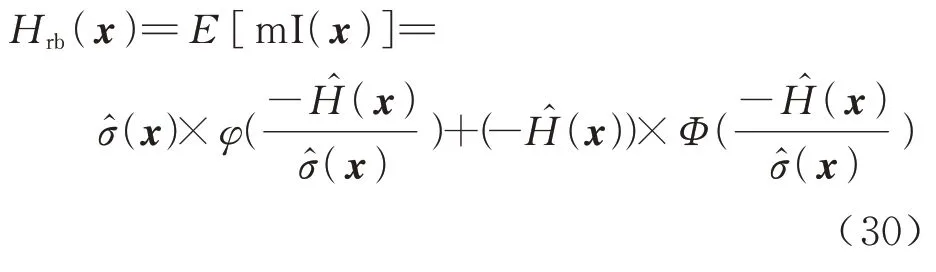
其中：Hrb(x)是改善程度函数的期望，即本文的主动学习函数；φ和Φ是标准正态分布的概率密度分布函数和累积分布函数。

定义E[mI(x)] 值最大的样本点为当前RBF 模型和此次抽样样本点集下的最佳样本点xb，即：

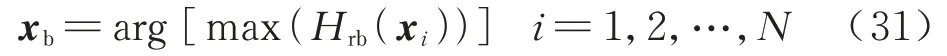
进而，得到xb点的真实响应并将其加入初始样本集S以更新RBF 模型。然后基于更新后的模型在候选样本点中选择新的最佳点，直到满足迭代停止条件。

通过对Hrb(x)求偏导可知：Hrb(x)与预测响应呈负相关，与jackknifing 方差呈正相关。预测响应值越小，学习函数Hrb(x)的值越大。因此，样本点的搜索区域主要在极限状态面附近，这增强了学习函数的局部搜索能力。此外，Hrb(x)和两者之间呈正相关，在主动学习过程中模型会在拟合不确定性较大的区域选择更多的样本点，从而增强了学习函数的全局搜索能力，防止模型陷入局部更新。

2.3.2 主动学习的收敛准则

一般而言，非概率可靠度的预测值会在若干步主动学习迭代后达到稳定状态，本文提出了如下的主动学习收敛准则：

其中：K表示为第K次迭代过程；是第i次迭代计算得到的非概率可靠度表示k次迭代过程计算得到的非概率可靠度的平均值；表示k次迭代计算得到的非概率可靠度的标准差。综合考虑精度和效率，本文中k取10，ɛ设置为1×10-3。

2.3.3 主要计算步骤

结合RBF 模型和2.3 节提出的主动学习方法，本文提出的算法主要步骤描述如下：

步骤1 抽取一个在超椭球域内均匀分布的大小为N的选样本集Sc={x1，x2，…，xN}。方法如下：

步骤a：在由各个变量的边缘区间构成的超立方体中均匀抽样得到足够多的样本。

步骤b：由式（10）计算步骤a 得到的每个样本的示性函数，如果示性函数的值为0，将其剔除，最终得到满足要求的N个候选样本，如果候选样本个数不满足要求，返回步骤a，调整抽样数，直至满足要求。

步骤2 采用拉丁超立方抽样（LHS）方法在由变量的边缘区间构成的超体方体内生成样本集X，然后计算X对应的真实响应Y得到构建 RBF 模型的初始样本集S={(x1，Y(x1))，(x2，Y(x2))，…，(xk，Y(xk))}。初始样本集的大小必须合适，最后基于初始样本集S构建RBF 模型。

步骤3 基于k折交叉验证方法，从S中得到10 个样本子集以构建RBF 模型。之后，用2.2 节中提到的jackknifing 方法估计候选样本点的jackknifing方差

步骤4 根据预测响应和jackknifing 方差计算所有候选样本点的学习函数值Hrb(·)。选择最大Hrb(·)值对应的样本点作为最佳点xb。

步骤5 根据1.3 节的MCS 方法计算由样本集S构建的代理模型的非概率可靠性度

步骤6 计算主动学习的收敛准则。判断RBF 模型精度是否满足要求。当收敛准则ε小于1×10-3时，转步骤7。否则，计算最佳点xb的真实响应Y(xb)，将样本(xb，Y(xb))加入到初始样本S中重新构建RBF 模型，返回步骤3。

步骤7 当RBF 模型精度满足要求时，通过MCS 估 计利用式（13）计算变 异系数，此时应确保变异系数小于5%。

3 实际算例验证

本节中提出了1 个数值算例和2 个工程算例，用于验证算法的有效性和准确性。由于在初始样本大小一定的情况下，初始样本的分布对收敛速度和精度影响很大，参照文献［29］，在每个算例中，生成4 组相同数目Case1～Case4，不同分布的初始样本集用于非概率可靠度的计算。此外，MCS 和文献［26］中的ERF 方法也用于解决这3 个例子，其中MCS方法得到的非概率可靠度将作为精确解。为了比较ERF 算法和本文算法的优劣，参照文献［26］，2 种算法初始均抽取12 样本点用于初始代理模型的构建，选取1×104个样本点作为候选样本点。最后，所有方法将从以下几个方面进行比较：①功能函数的调用次数Ncall用于衡量计算效率；②每种方法计算得出的非概率可靠度的相对误差用于衡量计算精度，相对误差ς表示为

3.1 数值算例

算例1 由经典的四串联系统［33］修改而来，考虑如下所示的串联系统：

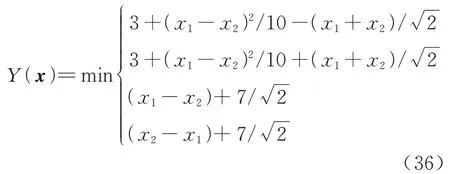
表1 给出了不同方法的计算结果，MCS 方法在椭圆域内抽取1×106个样本点，计算得到的非概率可靠性值为0.638 0；ERF 方法计算的非概率可靠度值为0.638 3，相对误差为0.047 02%；采用本文的方法计算得到的结果中相对误差最大为0.078 37%，从计算结果可以看出ERF 方法与本文的方法得到的非概率可靠度值均非常接近直接蒙特卡洛模拟的数值，2 种方法得到的结果均在可接受的范围内，都可以获得足够准确的结果。它们之间的主要差异在于对极限状态函数调用次数的大小。从表1 中的数据可以看出本文的方法调用功能函数的次数要明显小于ERF 方法，因此本文的方法相较于ERF 方法效率要高。

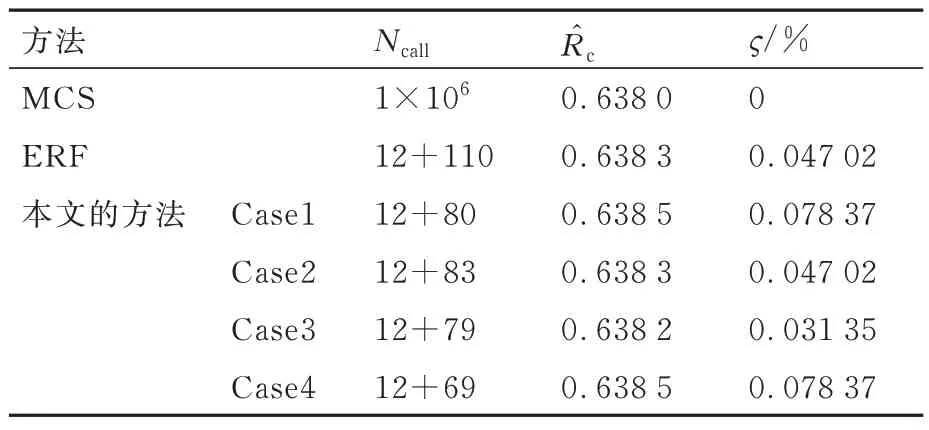
表1 算例1 的计算结果对比Table 1 Evaluation results of Example 1

如图4 所示，展示了本文的方法以及ERF 方法对极限状态面的拟合效果。ERF 方法和本文提出的方法均可以较好地对极限状态函数进行拟合。从图中可以看出本文所提出的方法可以较准确地获得真实极限状态面附近的样本点；此外，所有选取的样本点都均匀分布在真实状态面附近。而ERF 方法获取的样本点较为均匀，部分样本点出现在空白处。因此本文的方法选点能力要高于ERF 方法。图5 展示了不同初始样本下非概率可靠度和相应的收敛准则ε的收敛过程。从图5（a）可以看出在增加了近60 个样本点后4 个计算案例的都趋于收敛，当值稳定后，主动学习过程停止，由此可以看出本文提出的收敛准则的有效性。

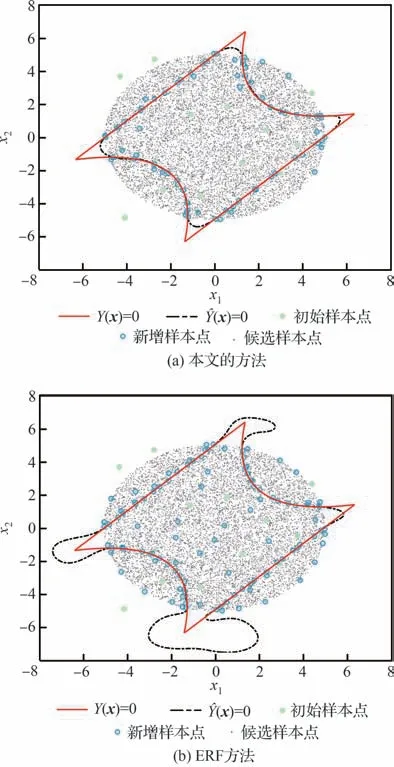
图4 算例 1 中不同主动学习方法的样本点分布对比Fig.4 Results of sample points computed by different active learning methods for Example l

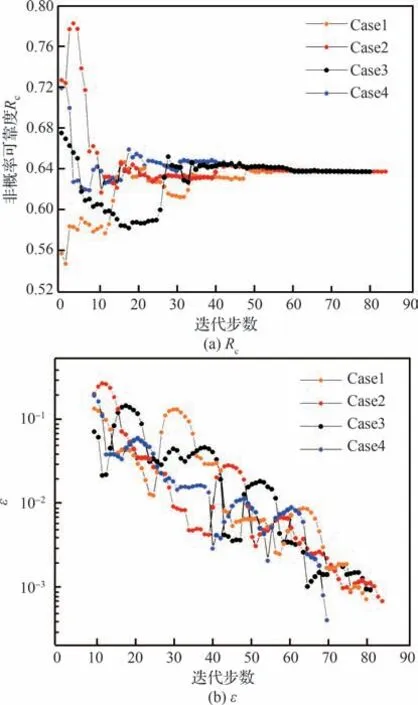
图5 算例1 不同计算案例的收敛过程Fig.5 Convergence process of different cases for Example 1

3.2 屋顶桁架

第2 个算例中分析了一个受均布荷载作用下的屋架如图6 所示，该算例修改自文献［9］。桁架的弦杆和压杆由钢筋混凝土制成，底部的弦杆和拉杆由钢制成。设屋架承受均布载荷q作用，将均布载荷q化成节点载荷后有P=ql/4。C点沿垂直地面方向的位移为。以屋架顶端C点的向下挠度不大于2.5 cm 为约束条件建立结构的极限状态函数：

图6 屋顶桁架示意图Fig.6 Schismatic view of roof truss

式中：q为均布荷载；l为桁架长度；Ac和As分别表示钢筋混凝土和钢筋的横截面积；Ec和Es表示相对应的弹性模量。该算例中6 个不确定参数的边缘区间如表2 所示。

表2 屋顶桁架的不确定变量参数Table 2 Uncertain variables for roof truss

不确定性区域可由一个超椭球模型来表示：

算例2 中不同方法计算得到的非概率可靠度和调用极限状态函数次数如表3 所示。采用本文的方法计算的4 个案例调用功能函数的次数大约在30 次左右，而ERF 方法需要调用40 次左右，采用本文的方法可以减少10 次左右的调用，因此本文的方法在计算效率上有所提高，同时计算精度上也提升了一个量级。所以，无论是计算精度（ς的大小）还是计算效率（Ncall），本文所提出的方法相较于ERF 方法均具有较好的优势。图7 展示了算例2 中不同初始样本条件下的收敛过程，随着样本点的不断增加，4 个计算案例均能收敛到较为理想的结果，表明该算法具有较好的鲁棒性。

表3 算例2 的计算对比Table 3 Evaluation results of Example 2

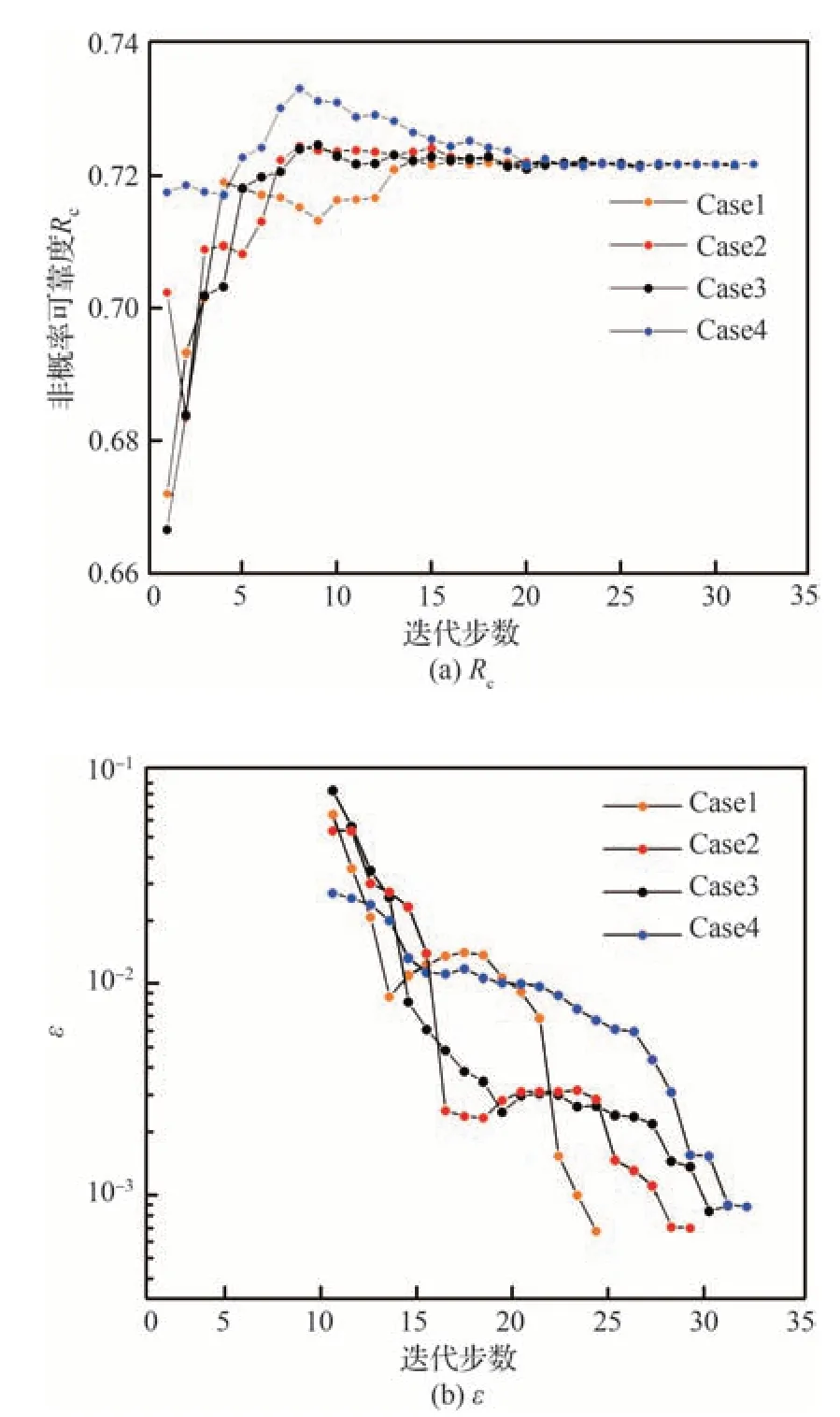
图7 算例2 不同计算案例的收敛过程Fig.7 Convergence process of different cases for Example 2

3.3 航空齿轮泵滑动轴承

为了尽可能地提高轴承支撑能力和结构强度，减小支撑结构的质量和体积，航空齿轮泵主要采用流体动压滑动轴承。如图8 所示是航空齿轮泵中滑动轴承的结构图及动压润滑压力分布示意图，图中齿轮轴的半径为rz，轴承半径为R，o和oi分别为轴承和齿轮轴的中心，轴承的半径间隙定义为C=R-rz，在齿轮轴与轴承之间的间隙中存在油膜。当齿轮轴以转速nr转动时，齿轮轴受到径向力F作用，发生偏心，导致齿轮轴中心oi和轴承中心o不重合，齿轮轴中心和轴承中心之间的距离为ed，定义滑动轴承的偏心率为e=ed/C。此时齿轮轴与轴承之间的油膜间隙变为楔形间隙。当齿轮泵正常工作时，滑动轴承收敛楔形间隙油膜满足动压形成条件，在楔形间隙会产生压力以承受径向载荷的动压润滑油膜，进而使滑动轴承正常工作。

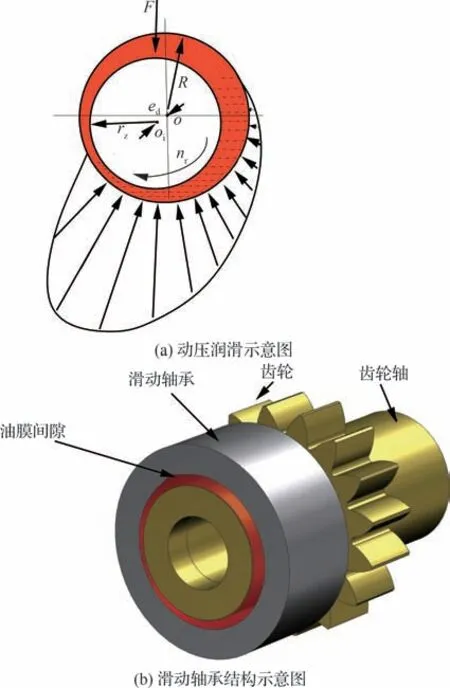
图8 某型航空齿轮泵中的滑动轴承结构及动压润滑压力分布图Fig.8 Sliding bearing structure and dynamic lubrication pressure distribution diagram of aviation gear pump

对于航空齿轮泵滑动轴承，如果齿轮轴和轴承相对运动产生的润滑动压超过材料所许可的压力，会造成轴承结构损坏。通过有限差分法求解Reynolds 润滑方程得到如图9 所示的油膜无量纲压力分布图，图中压力峰值点所在位置为轴承最容易失效部位，针对该点建立滑动轴承动压润滑极限状态方程：

图9 油膜压力分布Fig.9 Pressure distribution on oil film

式中：Pm是滑动轴承的许用压力，取值为2.4；P(x)为滑动轴承动压润滑的压力峰值；x为随机变量。本算例中随机变量x取为：轴承宽度B、轴承半径R、轴承半径间隙C、齿轮轴转速n、润滑介质黏度η、轴承偏心率e。6 个不确定参数的边缘区间如表4 所示。

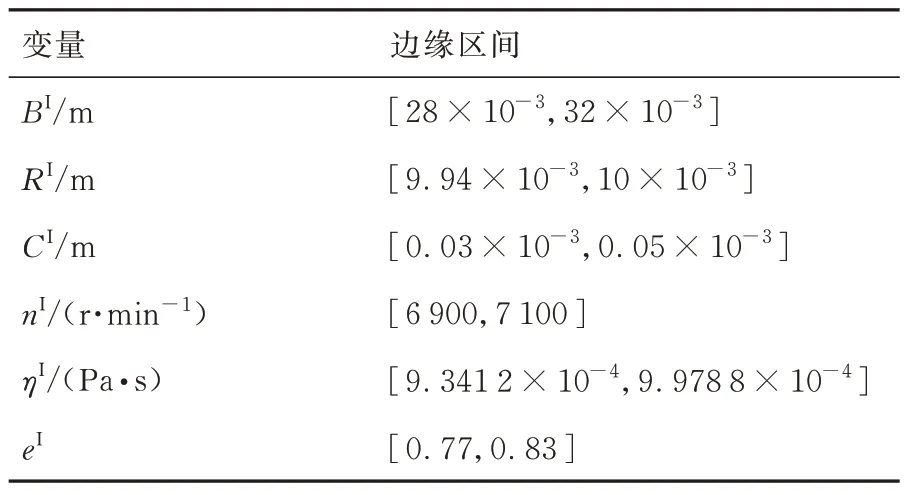
表4 航空齿轮泵滑动轴承的不确定变量参数Table 4 Uncertain variables for sliding bearings

不确定性区域可由一个超椭球模型来表示：

算例3 中不同方法计算得到的非概率可靠度和调用极限状态函数次数如表5 所示。ERF 方法计算的非概率可靠度值为0.836 6，相对误差为0.047 79%；采用本文的方法计算得到的结果中相对误差最大为0.059 74%，2 种方法都可以获得足够准确的结果。从调用极限状态函数的次数看，本文的方法调用极限状态函数的次数略少于ERF 方法，因此本文采用的方法计算效率要高于ERF 方法。不同初始样本下，迭代过程如图10 所示，从图10 可以看出，4 个计算案例新增样本数目很接近，同时随着样本点的不断更新，均能收敛到较为理想的结果。

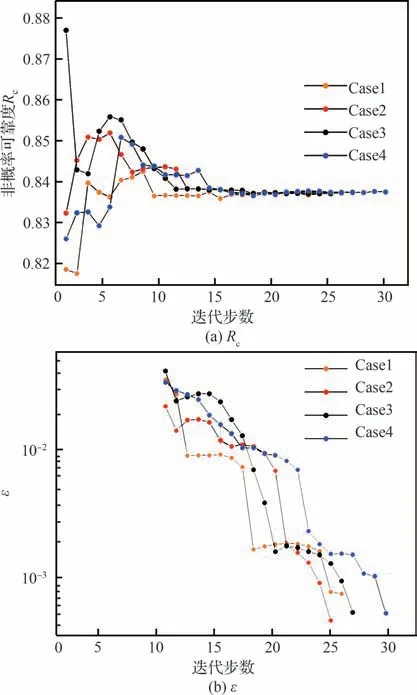
图10 算例3 不同计算案例的收敛过程Fig.10 Convergence process of different cases for Example 3

表5 算例3 的计算对比Table 5 Evaluation results of Example 3

4 结论

针对超椭球模型下非概率可靠度的求解问题，提出了一种采用RBF 模型的高效主动学习方法，该方法能在有限的样本点信息下，最大限度提高拟合精度，保证计算得到的非概率可靠度的正确性。

1）不同于传统的主动学习方法，本文结合交叉验证和jackknifing 方法推导出jackknifing 方差使得RBF 模型可以评估预测响应的不确定性，在此基础上将RBF 模型与主动学习相结合进行非概率可靠度的求解。由于算法基于RBF 模型构建，因此可以减少代理模型的建模复杂性同时可以消除Kriging 模型产生的结果不确定性。

2）提出了1 个数值算例和2 个工程算例来验证本文算法的有效性。此外，在每个算例中给出了由4 个不同初始样本计算得到的计算案例以验证所提出的算法的鲁棒性。分析结果表明本文提出的算法能够在较少计算功能函数次数的条件下，估算得到精确的非概率可靠度值，可以很好地满足工程应用要求。