基于模糊网络DEA 与Shapley 值的应急资源配置研究

朱佳翔，赵哲沁（常州大学 商学院，江苏 常州 213164）

0 引言

数据包络分析（Data Envelopment Analysis，DEA）是一种广泛使用的数学编程技术，最初是由Charnes 等人[1]开发，后由Banker 等人进行了拓展，经典的DEA 主要包括C2R、BC2、FG 与ST 等有限决策单元模型。在资源优化运用方面，文献[2-4]运用经典DEA 模型方法对物资配送效率进行评价。刘森等[5]将层次分析法与DEA 模型相结合，给出应急物资配送决策支持的定量方法。刘运昌等[6]运用超效率DEA 与ANP 相结合的方法，给出应急物流中心选址的策略。Lozano 等[7]研究了BBC 模型在资源配置及目标设定上的应用问题。文献[8-11]从系统整体视角研究集中式与分散式两种模式下的资源分配问题。但上述经典DEA 方法无法公正客观解决不确定环境下的资源配置问题。Lotfi 等[12]研究了决策单元为随机数据的DEA 方法，并用于解决集中式管理模式下的资源配置问题。Malek 等[13]研究了决策单元为区间数据的DEA 模型，通过数值分析验证该方法在解决集中式资源分配问题上的优势。

基于此，本文研究了有界可行域的模糊投入与产出问题，给出基于模糊网络DEA 与Shapley 值的评价方法，用于解决含模糊数据决策单元间的应急资源配置问题，进一步拓展模糊网络DEA 的应用范围。

1 模糊网络DEA

在给定的α 置信水平下，根据每个输入的模糊变量的上下界限与中间变量，推导出各自的隶属度函数表达式。参考文献[12]，决策单元DMUj整体效率的上下界限也可推算得到。

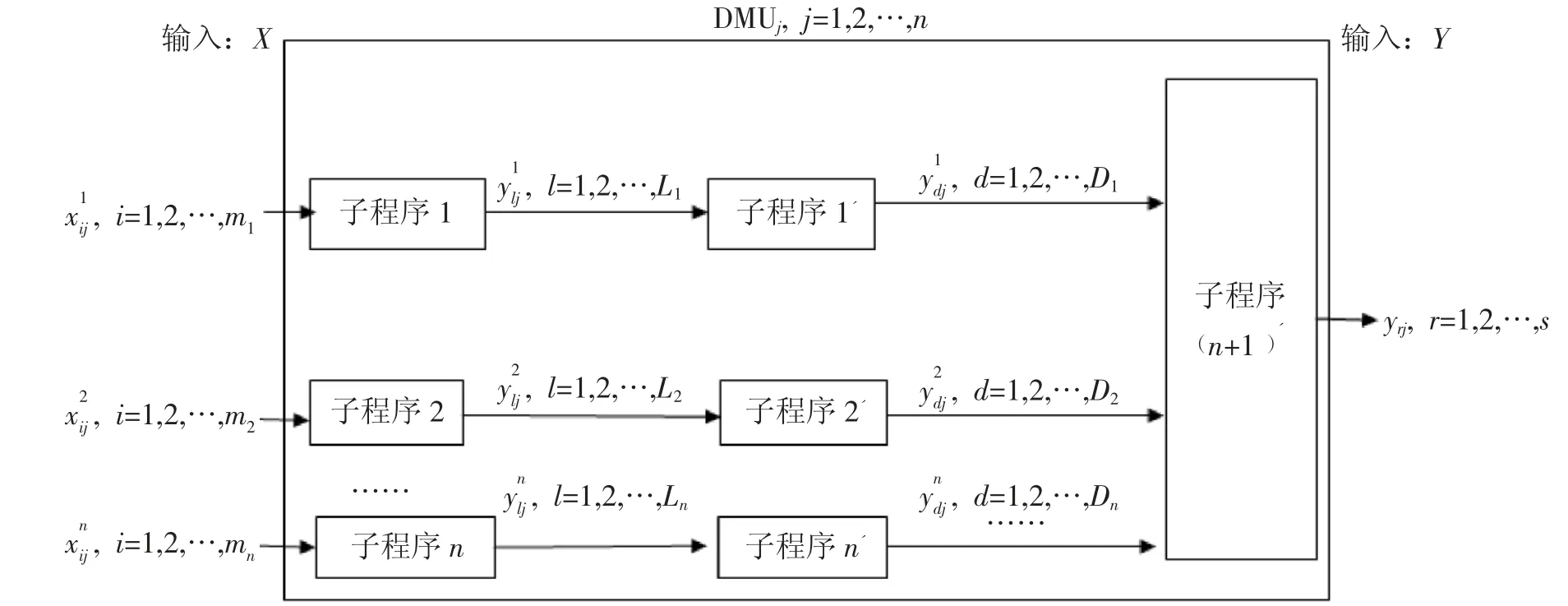
图1 模糊网络DEA 结构

2 改进的Shapley 值

Shapley 值在政治与经济领域广泛运用，是描述经济联盟体中参与者价值的函数，反映参与者对经济联盟体相对绩效的大小。如应急物流系统就是一个集应急资源仓储、运输与配送一体化的救灾联盟，可根据Shapley 值大小对应急物流系统中救灾联盟的应急资源配置进行决策。

若置信水平α 给定，对于∀S1∩S2=Ø，S1⊆N，S2⊆N，则有v（S1）+v（S2）≤v（S1∪S2）。

采用模糊网络DEA 测算各层决策单元的模糊效率，在此基础上运用改进的Shapley 值对应急资源进行合理分配，给定的算法步骤如下。

Step1：构建模糊网络DEA 的n 层输入输出网络，给出各个层次决策单元可能组成的救灾联盟；

Step2：给定的置信水平α 下，通过模糊网络DEA 方法计算救灾联盟各层中每个决策单元DMU 的模糊效率值；

Step3：根据改进的Shapley 函数的特征与表达式，计算应急物流系统中救灾联盟各层网络中的Shapley 值；Φ（v）=（φ1（v）,φ2（v）,…,φn（v））；Step4：计算应急物流系统中救灾联盟各层决策单元对系统整体的贡献率，根据贡献率大小对应急物流系统中应急资源R进行分配。模糊网络DEA 有n 层输入输出网络，在计算效率值时计算量大且复杂，可运用Matlab 软件实现。

3 数值算例

参考文献[13]，同时考虑地理位置与受灾物资配送等便利因素，以汶川地震为例，将汶川周边受灾较轻的三个县市，分别为A：茂县、B：理县、C：小金县等三县设定为应急物资配送中心，用于收集和供应救灾物资。同时，设定受灾较轻的六县市，分别为G1：陇南、G2：广元、G3：眉山、G4：雅安、G5：德阳、G6：乐山等六县市设定为应急物资供应源，用于运输救灾物资至4 个受灾区域，分别为区域1、区域2、区域3、区域4。输出指标相关模糊语言与隶属度设定为：非常低（VL）（0.1,0.2,0.3,0.4）；低（L）（0.2,0.3,0.4,0.5）；中低（ML）（0.3,0.4,0.5,0.6）；中（M）（0.4,0.5,0.6,0.7）；中高（MH）（0.5,0.6,0.7,0.8）；高（H）（0.6,0.7,0.8,0.9）；非常高（VH）（0.7,0.8,0.9,1.0）。构建的两层模糊网络各层的输入输出及其决策单元模糊评价语汇。4个受灾区域区间绩效得分以及DMU 与SDMU 分类如表1 所示。

表1 区间绩效得分以及DMU 与SDMU 分类

假定受灾区域获得应急资源总量R=10 000，根据上述算法步骤，在给定的置信度α 下安排应急资源分配方案，令置信度α=0.5，运用上述模糊网络DEA 测算出4 个决策单元在应急联盟体中的绩效值。可计算出决策单元DMU1、DMU2、DMU3、DMU4的Shapley 值分别为：0.683、0.785、0.736、0.768，再得到各个决策单元的分配比例，因此应急资源R=10 000 在各个决策单元中的分配方案为：2 298、2 642、2 476、2 584。假若应急物流系统中救灾联盟决策者可根据自身的风险偏好，适度调整差异化的置信水平，以致影响到Shapley 值，也将最终影响应急资源的分配方案，进一步计算出不同置信水平下的应急资源分配方案如表2 所示。

由表2 可知，随着置信水平的提升，模糊网络DEA 的决策单元效率值也在逐渐提高，对于输出型决策单元DMU1、DMU3来说，输出效率值越高则说明相对效率越低，因此，应急资源分配的份额逐渐降低。而输入型决策单元DMU2、DMU4随着置信水平的提升，则出现效率值不变的情景，但分配份额不断提高，说明决策单元DMU2、DMU4对应急物流系统的贡献越来越高。基于模糊网络单线分析，仅能判断上述4 个决策单元存在相对有效性，但不能给出其对应急物流系统的贡献大小，而融合了改进的Shapley 值的模糊网络DEA 方法，能够客观评价各个决策单元对系统的贡献度，将应急资源在应急物流系统的各个单元间进行公平配置。

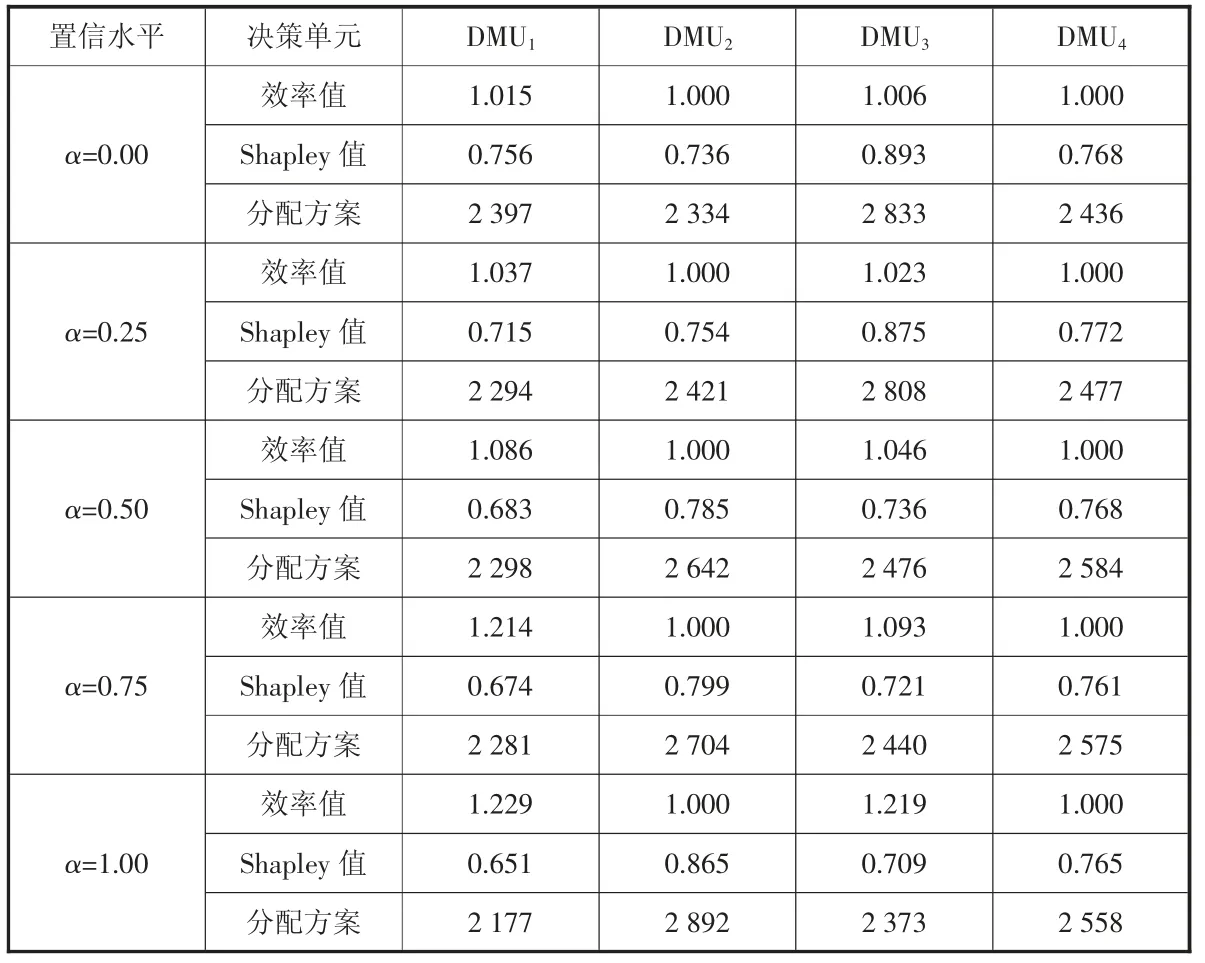
表2 不同置信水平下的应急资源分配方案

4 结论与讨论

针对应急物流系统中应急资源分配问题，本文在模糊网络DEA 界定基础上给出模糊网络DEA 内部结构。在置信水平α 给定的假设前提下，给出模糊网络DEA 方法，在有界可行域的应急物流系统投入与产出效率评价上，具有重要的应用价值。

Shapley 值反映应急物流系统中决策单元对整个系统的贡献大小，通过改进的Shapley 值与模糊网络DEA 输出效率值相结合，给出改进的Shapley 值以反映模糊决策单元对应急物流系统贡献情况。同时，结合救灾环境下应急物流系统运行的实际需要，给定的投入产出数据为模糊数据时，将模糊网络DEA 的效率值转化为改进的Shapley 值，并对应急资源分配方案的求解方法进行验证，进一步给出不同置信水平下应急资源分配方案的变动情景。在未来研究中，可将该方法推广应用于应急物流系统多阶段资源配置上。