基于混合遗传算法的城市固体废弃物运输路径优化研究

刘 华，武 峰（西安建筑科技大学 管理学院，陕西 西安 710055）

0 引言

随着城市化进程不断推进，城市生活固体废弃物产生量持续增长，同时居民的环保和健康意识也不断加强，如何管理城市生活固体废弃物已经成为居民和政府关注的重要问题，也受到了学术界的广泛关注[1]。生活固体废弃物的运输环节作为城市生活固体废弃物管理的重要组成部分，对其进行优化不仅可以提高废弃物的回收处理速度以及降低处理成本，而且能有效地解决运输过程中由于粗放运输方式所导致的一系列环境问题，同时也可为有关部门相关决策提供理论指导。车辆路径优化问题（Vehicle Routing Problem，VRP）正是固体废弃物运输路径研究的核心问题，最早是由Dantzig 和Ramser 提出的，问题可描述为：有一个起点和若干个客户点，在已知客户需求以及客户位置的条件下，规划最优路径，车辆从起点出发遍历所有客户点后回到起点，并使得总距离最短[2]。在城市生活固体废弃物运输系统中，废弃物回收站可以看为起点，垃圾产生点为客户点。在废弃物运输过程中，城市处理能力及其政策法规对运输时间进行限制，即运输必须在废弃物收集点的时间窗（Time Windows）内进行。由此在传统VRP 的问题上引出了带时间窗的车辆路径问题（Vehicle Routing Problem Time Windows，WRPTW）。

VRPTW 问题属于NP-hard 问题，同时由于约束条件复杂，随着客户数目的增加，求解的难度较大。算法的优劣将直接影响求解的效率和质量，因此学者一直致力于寻找更高效的求解算法。针对于VRPTW 问题。Orivalde S.Silva Júnior 等利用多重蚁群系统（MACS）和随机变量邻域下降（RVND）提出了MACS-RVND 算法[3]。Raúl Baños 等提出了一种基于模拟退火的多目标优化算法——多温度Pareto 模拟退火算法（MT-PSA）[4]。Konstantakopoulos Grigorios D 等提出了一多目标优化的大规模邻域搜索算法（MOLNS）[5]。孙沪增等针对蚁群算法局部搜索能力不足以及容易陷入早熟的缺点，通过改进的状态转移规则并多种局部搜索算子来改进蚁群算法[6]。陈久梅等针对开放式带时间窗问题，设计了变邻域搜索算法，拥有较好的收敛性和稳定性[7]。李珺等利用贪婪插入法构建初始解，在细菌觅食算法中引入了大邻域搜索方法Removal 算子，扩大了求解算法的搜索空间[8]。张建同等针对模拟退火算法求解VRPTW 问题时容易早熟的问题，在算法中引入了变邻域搜索算法提出了SAVN，实践证明添加后能够显著提升算法跳出局部最优解的能力[9]。张瑾等对客户点按其所在位置进行聚类分析，在蝙蝠算法中引入了变步长搜索策略和两元素优化方法进行局部搜索，提高算法的求解效率[10]。张晓楠等通过在运用简化的变邻域搜索进行局部开发，引入邻域半径减少策略提出了混合Memetic 算法用于求解VRPTW 问题，研究表明算法能够搜索到更好的路径[11]。黄震等在蚁群算法中将遗传算法中的交叉、变异机制提出了混合遗传算法，用于提高算法的求解效率[12]。何小锋等通过定义人工蚂蚁的转移概率，增加量子比特启发式因子，以及用量子旋转门实现信息素更新提出了量子蚁群算法（QACA），研究表明能够提高算法的全局搜索能力[13]。

总体来看，元启发式算法当前拥有较为丰富的研究成果，相较于精确式算法和启发式算法拥有更好的求解效率，而且更适合大规模求解。遗传算法（GA）是模拟生物进化过程，通过选择、交叉和变异机制来实现最优解的探索，同时遗传算法也被广泛应用于求解VRPTW 问题，然而遗传算法同时存在局部搜索能力不足，过早陷入局部最优的缺点，当问题规模增大或约束增加时，往往不能得到好的结果。变邻域搜索算法（VNS）则是采用多种邻域变化，可以和其他元启发式算法进行结合来提升算法的局部搜索能力，提高求解效率。因此本文将VNS 算法中邻域搜索与GA 算法进行结合，提出混合遗传算法用于求解VRPTW 问题。

1 城市固体废弃物运输路径优化模型

本问题可描述为有1 个废弃物回收站0，和n 个废弃物产生点，可定义为一个无向连通图G=（V,L），其中V=｛0,1 ,…,n ｝为节点，其中0 为中转中心，V/0 为收集点。E 为连接节点的边集合，E=｛（i,j）|i,j∈V,i≠j ｝。中转中心有K 辆运输车辆，车辆的最大装载能力为Q，每个收集点有确定废弃物处理量di，每个收集点只能由一辆运输车完成收集，同时每辆车只能服务一条路径，运输车辆必须在废弃物产生点的时间窗内进行配送。根据以上对VRPTW 问题的描述，可构建数学模型如下：

式（1）为目标函数，其中第一部分为车辆固定成本，主要取决于车辆的使用数目，第二部分为可变成本，与车辆的行驶距离有关，两者之和为车辆的总成本费用。式（2）、式（3）表示车辆从废弃物回收点出发最终返回回收点。式（4）表示废弃物产生点i 只接受一辆车的配送服务。式（5）表示车辆运输服务必须在废弃物产生点的时间窗内进行。式（6）是用于确保运输服务的连续性，其中M 为一个大的正值。式（7）为车辆载重约束，式（8）为0～1 约束。变量具体含义如表1 所示。

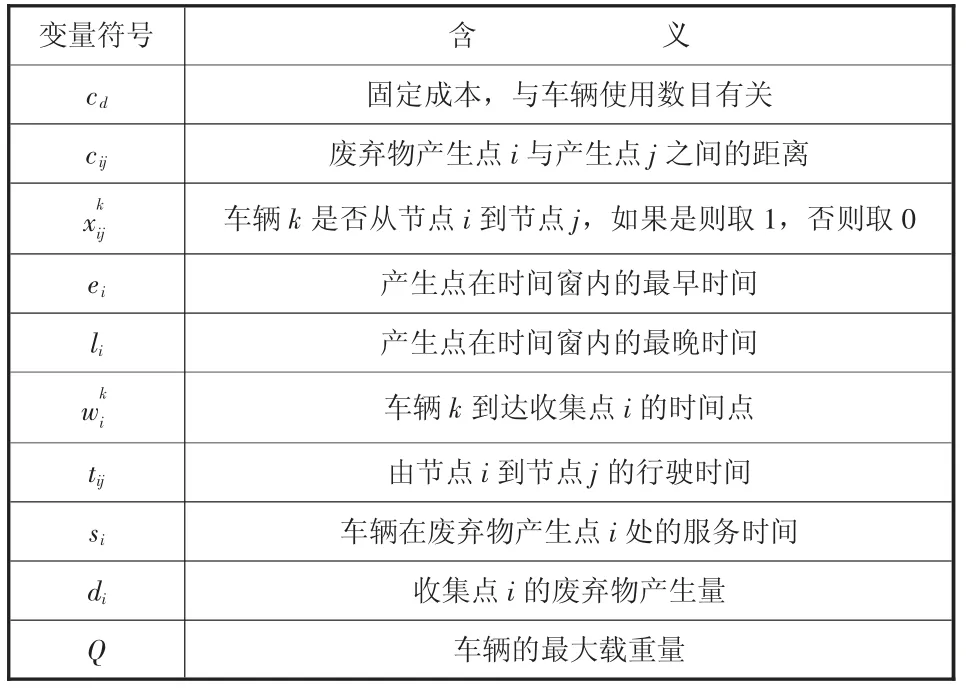
表1 变量符号说明

2 算法设计

考虑到遗传算法的缺陷，本文对遗传算法做出以下改进。一是引入自适应交叉变异和最优个体保留策略来提升算法的求解效率。二是在变异算子中，引入变邻域搜索增强算法的局部搜索能力。算法流程如图1 所示。

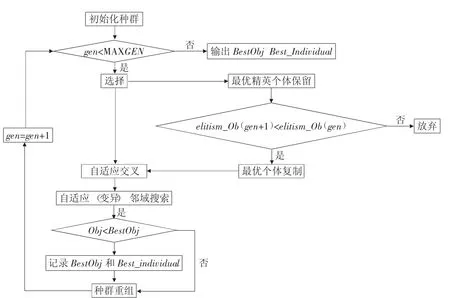
图1 算法流程图

2.1 初始化种群

初始解能够直接影响算法的求解效率，随机生成解能够丰富解集空间，是较为常用的初始化种群方法，然而本文研究的VRPTW 问题会受到车辆载重约束和服务时间窗约束，如果选择随机初始化种群则会不可避免地产生大量的无效解。因此，本文采用遍历废弃物产生点的方法，首先随机生成废弃物产生点序列C，以载重约束为主约束，将产生点c1,c2,…,cn依次添加到车辆ki行驶的路径节点中，当超过车辆k 的最大载重时，此时新派一辆车，直到将所有收集点都添加到路径中，与此同时将每条路径内的收集点的顺序进行调整，通过计算车辆到达的收集点时间，并与废弃物产生点的时间窗进行对比从而完成路线内调整，当难以满足条件时，则新增车辆。这样既能够保证初始解的有效性，提高算法的效率，同时采用随机序列又能够兼顾种群多样性，提高搜索空间。本文的染色体编码采用整数编码的方式，以8 个垃圾收集点节点为例，如图2 所示。

图2 编码方式

其中节点9 和节点10 为虚拟的废弃物回收站，作为不同车辆路径的分界，故车辆1 的行驶路径为：0→2→4→1→3→0；车辆2 的行驶路径为：0→5→7→0；车辆3 的行驶路径为：0→6→8→0。

2.2 适应度函数

适应度作为个体质量的衡量标准，与个体被选择的概率成正相关关系。由于在求解过程中难以确保满足时间窗约束和载重量约束，因此采用惩罚函数的方法用来解决违反约束的问题。分别建立时间窗约束惩罚函数T（s）和载重约束惩罚函数Q（s）并与目标函数中的总成本进行加和。将其倒数作为求解过程中的适应度函数。

时间窗约束惩罚函数：

其中：ti为到达收集点i 的时间，ei和li分别为废弃物产生点i 的左右时间窗，w1和w2为早到和晚到的惩罚参数。

载重约束惩罚函数：

其中：di为收集点i 的废弃物产生量，Q 为车辆的最大载重量，w3为超载惩罚参数。

2.3 选择算子

选择操作是从种群中选择适应度高的个体产生新群体的过程，选择出良好的个体形成新的种群能够提高收敛速度。轮盘赌法、锦标赛法是较为常见的选择算子，已有研究表明锦标赛选择策略比轮盘赌选择策略具有更好的通用性，且性能更优[14]。因此本文采用二元锦标赛法，具体操作为从种群中随机选择一对个体，通过对比两者的适应度，选择适应度高的个体进入下一代，剔除重复个体形成新的种群。

2.4 交叉算子

交叉算子能够提高遗传算法的全局搜索能力，是指将两个个体中的部分结构进行替换完成重组，生成两个新的个体。本文采用部分匹配交叉（PMX），具体操作为随机生成两个交叉点，交换两条染色体的交叉片段，同时删除染色体中的重复遍历点。将重复遍历点重新插入染色体，如图3 所示。

图3 交叉算子

2.5 变异算子

遗传算法中变异算子能够提高算法的局部搜索能力，避免算法陷入局部最优。本文采用变邻域搜索（VNS）来完成遗传算法中的变异操作，采用Insert、Swap 和Reverse 三个搜索算子进行变邻域搜索。Insert 算子是随机选择两个节点，将第一个节点插入到第二节点。Swap 算子是随机选择两个不同的节点，将其交换位置。Reverse 算子是逆转两个位置之间所有城市的顺序。具体如图4、图5、图6 所示。

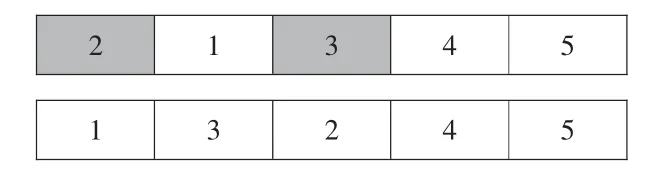
图4 Insert 算子

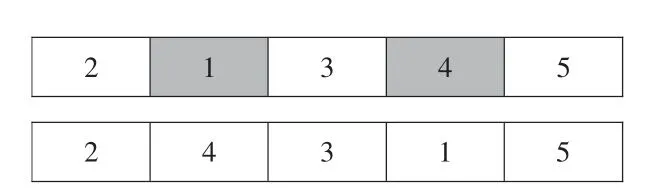
图5 Swap 算子

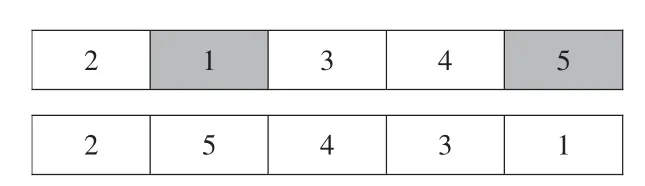
图6 Reverse 算子

本文采用轮盘赌法来随机选择邻域，每当完成一个邻域搜索后再随机选择下一个邻域进行搜索。每当完成一次邻域搜索，将当前解与当前最优解进行对比。为了进一步提高算法的效率避免因陷入局部最优，导致算法将无法跳出当前最优解。因此本文借鉴模拟退火算法的Metropolis 准则，如果能够以一定概率接受比局部最优解的稍差的解将有助于算法跳出局部最优解。计算公式如式（11）所示。

其中：f（Scurr）为当前解的目标值，f（Snew）为新解的目标值，k 为当前邻域的迭代次数，Kmax为最大邻域最大迭代次数，P 为接受新解的概率。

局部搜索流程如图7 所示。

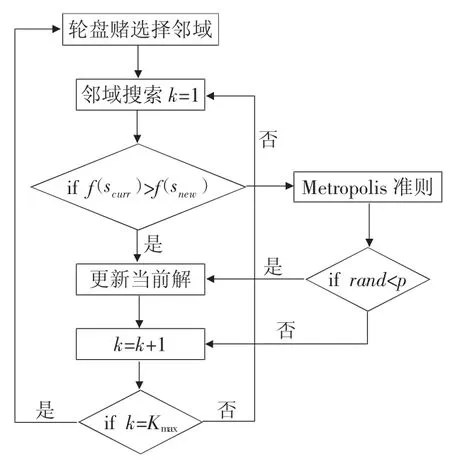
图7 局部搜索流程图

2.6 自适应交叉和变异概率

标准遗传算法中，交叉概率和变异概率一般被设为定值。为了提高求解速率，在迭代前期，通常可以设置较大的交叉概率来增强算法的全局搜索能力，提高搜索速度，而迭代后期，较低的交叉概率和较高的变异概率能够减少对最优解的破坏，同时增加算法的局部搜索能力。相比于常规的交叉变异概率，自适应交叉、变异可以算法的进程动态的调整其概率。基于以上分析，本文参考文献[15]，设置了自适应交叉和变异概率，计算公式如下所示。

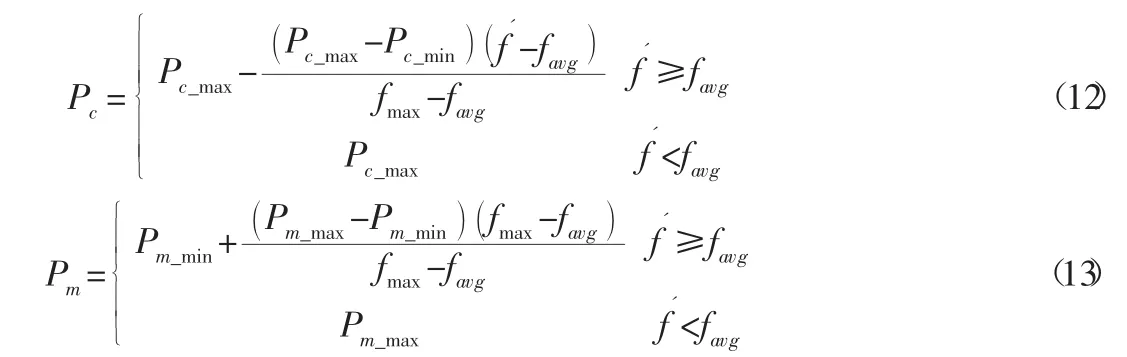
其中：Pc_max和Pc_min分别是交叉概率区间的最大值和最小值，Pm_max和Pm_min分别为变异概率区间的最大值和最小值，f 为个体适应度值，f'为进行交叉父本中最优个体的适应度值，fmax前种群中最优个体的适应度，favg为当前种群中的平均适应度。

2.7 最优个体保留策略

为了防止种群中的优秀个体在迭代过程中遭到破坏，本文采用最优个体保留策略，如式（14）所示。在迭代过程中将第n-1 代种群中最优个体I 进行复制保留，如果经过交叉、变异等操作后，此时生成新的个体I，如果此时f（I）＞f（I'），则用个体I 替换个体I'最优个体保留策略能够在一定程度上保护有效基因，提高算法的计算效率，同时也尽可能避免了对遗传法则的破坏。

3 算例设计

3.1 算法验证

本文选择Solomen 算例中7 个标准例题对本文提出GA_VNS 算法进行测试，本文设置种群为150，最大迭代次数为250。其中对混合遗传算法设置Pc_max和Pc_min为0.9 和0.5，Pm_max和Pm_min为0.2 和0.02。算例求解结果如表2 所示。

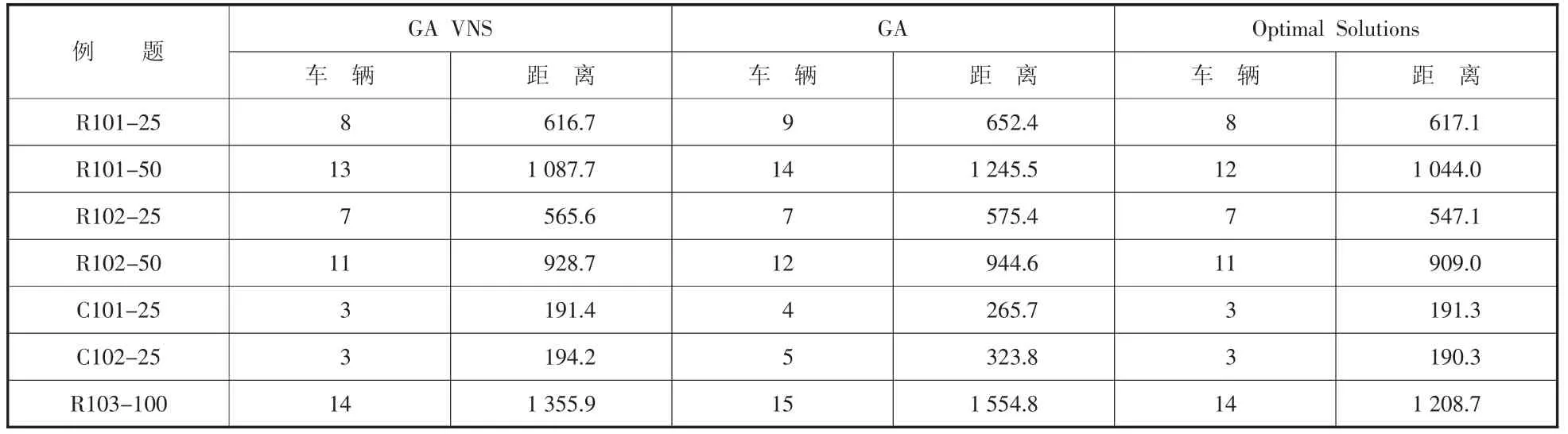
表2 算例求解结果

分析结果表明，相较于标准遗传算法，本文所提出的GA_VNS 能够得到更优的求解结果，在求解R101-25 例题时具有显著的效果，R101-25 迭代过程如图8 所示，R101-25 最优路线图如图9 所示。由于算法中的参数设置是由多次实验得出，因此求解大规模算例仍存在一定的改进空间。

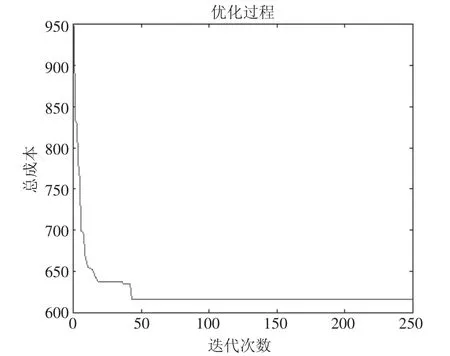
图8 R101-25 迭代过程图

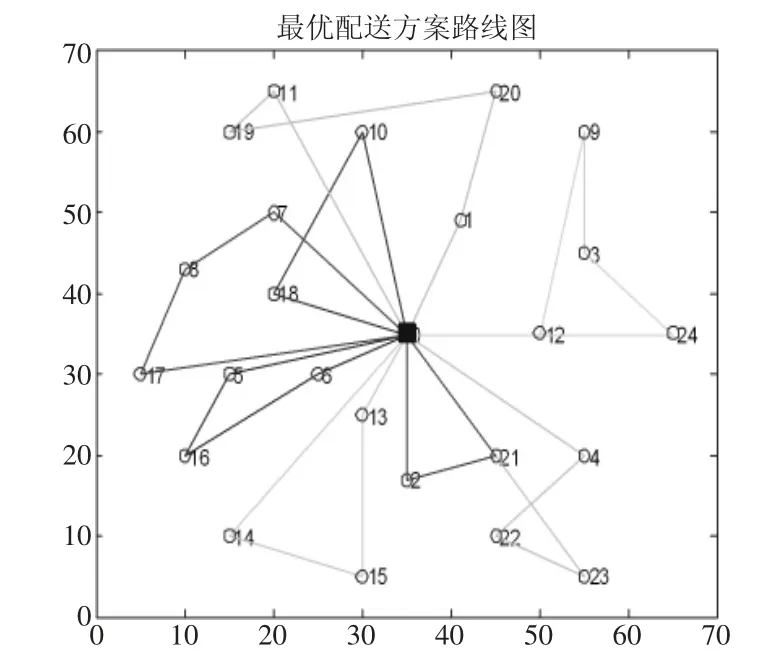
图9 R101-25 最优路线图

3.2 算例设计

某废弃物回收站坐标为（30,30），共有4 辆废弃物运输车，每辆车最大载重为150。该处理点需要收运周围20 个废弃物产生点所产生的垃圾，假设单位用车成本为200，单位距离的成本为30。废弃物回收站及各废弃物产生点具体信息如表3 所示。为了方便计算，将两个节点的直线距离作为两点的路程。

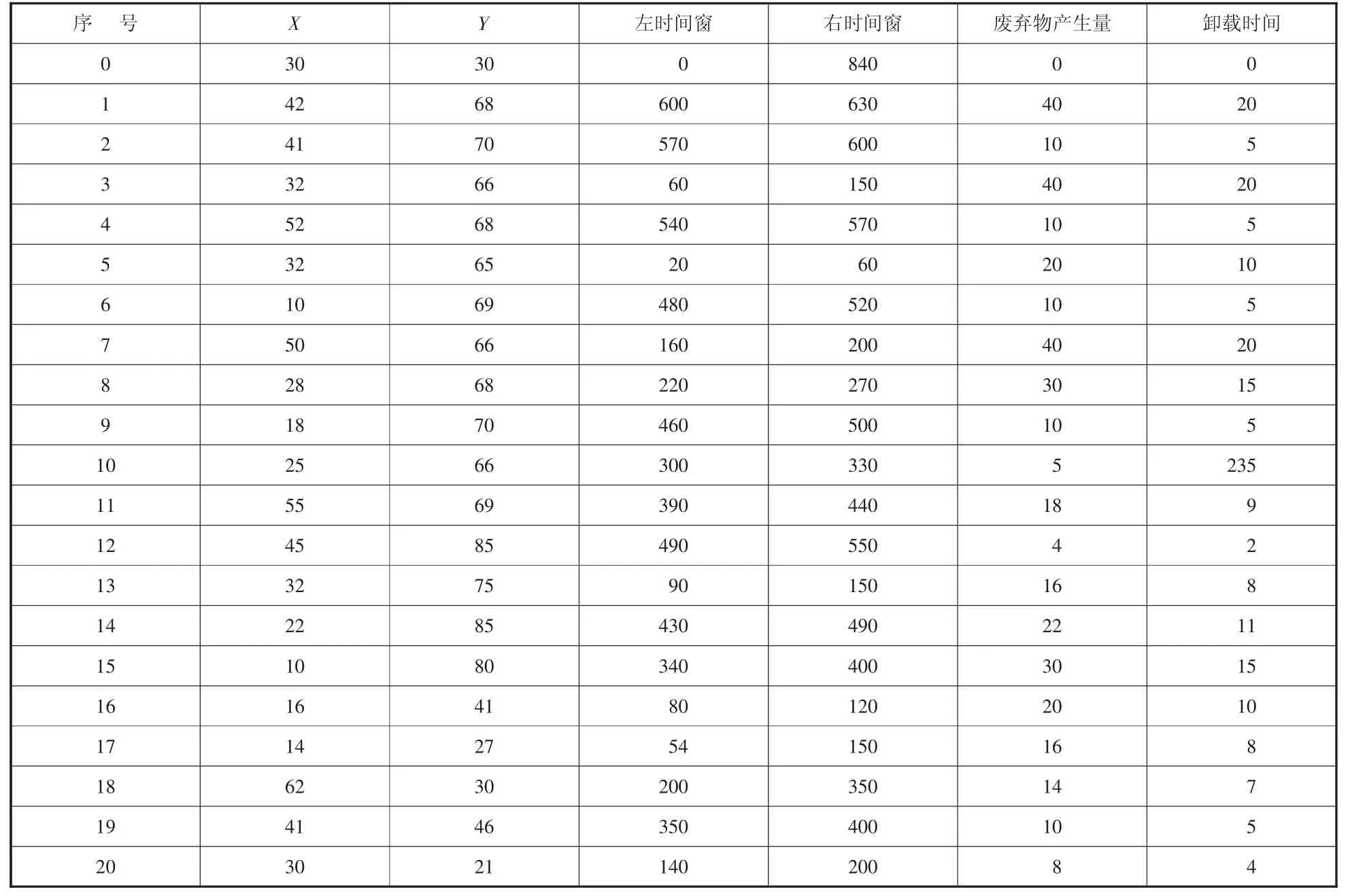
表3 废弃物回收站及产生点信息表

在本算例中设置最大迭代次数为250，设置种群为150，设置Pc_max为0.9，Pc_min为0.5，Pm_max为0.2，Pm_min为0.02。根据以上条件，求得结果如表4 所示。经过验证，三条运输路径均满足收集点的时间窗约束和车辆载重约束，因此验证了本算法在城市生活固体废弃物运输系统问题中的有效性。本算例迭代过程和最优配送路线如图10 和图11 所示。

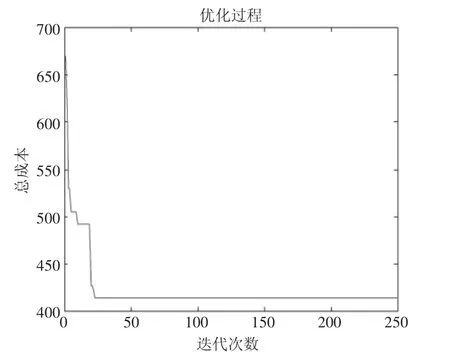
图10 迭代过程图

表4 算例求解结果

4 总结与展望

本文以总运输费用最小为优化目标提出了城市生活固体废弃物运输路线优化模型，进而提出了一种混合遗传算法（GA_VNS），将变邻域搜索的思想和遗传算法进行结合，并采用了Swap、Insertion 和Reverse 三种邻域搜索算子对遗传算法的变异算子进行改进，同时采用模拟退火算法中的Metropolis 判定规则用于更新邻域搜索的最优解，并采用自适应的交叉变异概率和最优个体保留策略，用于提高遗传算法的局部搜索能力，有助于算法跳出局部最优。

实验结果表明，与标准遗传算法相比，本文所提出的混合遗传算法拥有更好的求解效率，能够得到比遗传算法得到更优的配送路径。从实验结果来看，该算法能够快速找出小规模问题的最优解，对于大规模问题的求解由于实验中算法参数是经过多次实验得到，因此离最优解仍存在一定的差距。对于后续研究将继续从邻域搜索的角度入手，设置邻域的搜索算子、动态调整邻域搜索的最大搜索次数，以及自适应的Metropolis 判别准则将是以后研究的重要工作。